Connection between macroscopic kinetic measurables and the degree of rate control†
Received
21st June 2017
, Accepted 16th August 2017
First published on 16th August 2017
Abstract
Catalytic reactions are commonly characterized by measuring reaction orders and apparent activation energies. In the present work, these macroscopic measurables are related to the degree of rate control (χi), which describes how the overall kinetics is influenced by the elementary reactions. The reaction orders are found to be χi-weighted sums over the microscopic rates, derived with respect to pressure. Similarly, the apparent activation energy is shown to be a sum over the individual reaction-energy-barriers, weighted by χi. The results couple macroscopic kinetics to the microscopic scale, which can facilitate analysis of catalytic reaction kinetics.
1 Introduction
The steady-state kinetics of a heterogeneous catalytic reaction is often analyzed using macroscopic measurables such as reaction orders and apparent activation energies. Although such phenomenological measurables characterize the reaction, their physical interpretation and microscopic origin are commonly unclear. This difficulty in interpretation could be present even for reactions where a detailed mechanism has been formulated.
On the microscopic (elementary reaction) level, the degree of rate control (χi) determines the influence of an elementary step on the total rate. χi of a reaction step i was introduced in ref. 1 as the partial derivative of the total rate (r) with respect to the rate constant of the considered step:
| | 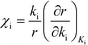 | (1) |
The derivative is taken while keeping the equilibrium constant (Ki) of the investigated reaction step fixed. In practice, this implies increasing the forward and backward rate constant of the considered step by a small percentage and calculating the response in the total rate. A reaction step influences the overall rate if χi is non-zero. For a positive χi, the step is rate-controlling, whereas for a negative χi, it is inhibiting. If χi is unity, i is the rate-determining step.1
χ
i has frequently been used to analyze first-principles microkinetic models,2–11 and recently as a tool for computational catalyst screening.11χi has also been used to analyze experimentally derived microkinetic models.12 Despite χi being a versatile tool, its relation to characteristic measurable quantities such as the reaction orders and apparent activation energies has not been fully established. This is unfortunate as the degree of rate control could offer a clear physical interpretation of the phenomenological measurables. Ref. 8 provided an expression for the relation between the χi and the apparent activation energy. However, this was derived assuming a vanishing derivative of the pre-exponential factors with respect to temperature and without pressure effects, which is not generally applicable.
Herein, we derive the connection between the reaction orders, apparent activation energies and χi under generally applicable assumptions of steady-state kinetics. We find that the reaction order is a weighted sum over the individual reaction rates, derived with respect to pressure. Similarly, the apparent activation energy is given by the sum of the individual energy barriers, weighted by χi. Interpreting χi as weights in the sums relies on the fact that 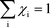 , which is proven in Appendix A. The derived relations provide a clear interpretation of the macroscopic measurables in terms of elementary reaction steps. This is important as reaction orders and apparent activation energies are parameters in phenomenological rate expressions. The relation between global and detailed kinetic parameters should facilitate the understanding and development of catalytic processes.
, which is proven in Appendix A. The derived relations provide a clear interpretation of the macroscopic measurables in terms of elementary reaction steps. This is important as reaction orders and apparent activation energies are parameters in phenomenological rate expressions. The relation between global and detailed kinetic parameters should facilitate the understanding and development of catalytic processes.
2 Reaction order
The reaction order nX in the pressure of species X is a phenomenological quantity that describes how the rate scales with the pressure. The reaction order is obtained assuming a power-law of the total rate in the pressure:| | 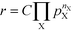 | (2) |
where r is the total rate, C is a constant, and pX is the partial pressure of species X. The reaction order is the logarithmic derivative of nX with respect to pX:| | 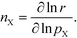 | (3) |
The total rate is a function of the rates of the elementary reactions (Wi) that in turn depend on the rate constants:
| | r = r[Wi[kj(T,![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) pX, pX,![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Gj)]]. Gj)]]. | (4) |
where
Gj are the Gibbs free energy barriers for the elementary steps. Consequently, the reaction order can be rewritten as:
| | 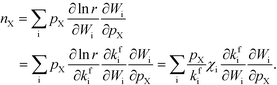 | (5) |
where
kfi is the forward rate constant. The derivatives are taken while keeping the equilibrium constant (
Ki) fixed, in accordance with the definition of
χi in
eqn (1). This is implicit in the remaining derivations. The expression for
nX can be simplified by considering
Wi in the mean-field picture, where the coverages (
θ) determine the rates.
Wi can be written in the mean-field picture as:
| | 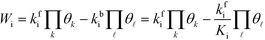 | (6) |
where
kbi is the backward rate constant. Note that the pressure factor in the case of adsorption reactions is intrinsic in
kfi. Assuming that the coverages have vanishing derivatives with respect to
Wi, the derivative of the rate constant becomes:
| | 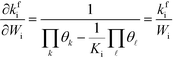 | (7) |
Finally, the reaction order takes the form:
| | 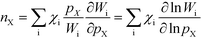 | (8) |
This expression conceptually relates the reaction order to χi through a weighted sum over the rate-controlling steps. Thus, the reaction order reflects both the degree of rate control and the change of Wi with pressure. The derivative entering the sum reflects the response of the individual rates to a change in pressure. This is the analog of the reaction order for an elementary step. The relation is particularly simple to interpret when there is only one rate-determining step, and the reaction order reflects how the pressure influences this step. Furthermore, the reaction order can take various values depending on the stoichiometric number of the reactions and the coverages. In the derivation of eqn (8), we assume that the coverages are unaffected by small changes in the rate constants. This is a valid assumption for steady-state kinetics far from kinetic phase transitions.
3 Apparent activation energy
The apparent activation energy, Eapp, is a macroscopic quantity that reflects the overall activation energy of a catalytic reaction. It is accessible from experimental studies where the catalytic rate is measured as a function of temperature. Eapp is obtained assuming an Arrhenius relation in the catalytic rate (r):| | 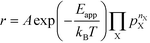 | (9) |
where A is the pre-exponential factor, X is a gas-phase species, pX is the partial pressure, and nX is the reaction order. The factor 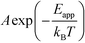 is known as the rate constant of the reaction (k). In general, it is not clear if a rate-law such as eqn (9) can fully describe the reaction. However, assuming that it is valid, it is interesting to analyze what factors contribute to the apparent activation energy.
is known as the rate constant of the reaction (k). In general, it is not clear if a rate-law such as eqn (9) can fully describe the reaction. However, assuming that it is valid, it is interesting to analyze what factors contribute to the apparent activation energy.
In practice, Eapp is found as the logarithmic derivative of k with respect to T:
| | 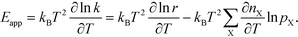 | (10) |
The relation between Eapp and χi is derived by recognizing that the rate is a function of the rate constants (ki), which in turn are functions of the temperature. Using the chain-rule for differentiation on eqn (10) gives:
| | 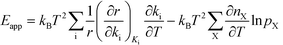 | (11) |
This derivative is again taken while keeping the equilibrium constant of each reaction fixed. The derivative of the rate constant ki with respect to temperature is:
| | 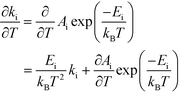 | (12) |
where
Ai is a pre-exponential factor of step i. Inserting this expression in
eqn (11) yields:
| | 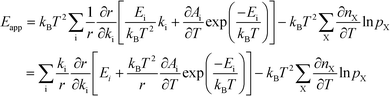 | (13) |
The first term can readily be recognized as χi multiplied by Ei:
| | 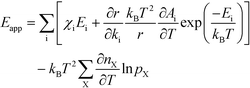 | (14) |
A
i needs to be defined to analyze the second term. For a surface reaction we assume that a vibrational degree of freedom is lost when reaching the transition state. Transition state theory13 gives in this case:
| | 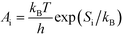 | (15) |
where
Si is the entropic barrier for going to the transition state. The derivative can be evaluated in this case as:
| | 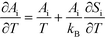 | (16) |
For an adsorption reaction, the reaction coordinate is typically a translational degree of freedom, and a collision theory pre-exponential factor is appropriate:
| | 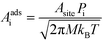 | (17) |
where
Pi is the sticking probability, which accounts for entropic barriers of adsorption. Hence, the derivative for an adsorption reaction is:
| | 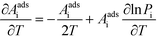 | (18) |
The final expression is obtained by inserting eqn (16) and (18) into (14):
| | 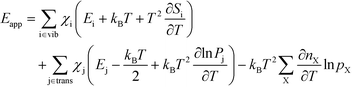 | (19) |
The first sum runs over all reactions that proceed via a vibrational reaction coordinate (surface and desorption reactions), whereas the second sum runs over adsorption steps that proceed via a translational degree of freedom. The third sum accounts for pressure effects through the reaction orders. The first order contribution in temperature comes from the reaction-coordinate, and the second order contribution stems from entropic barriers and pressure. The fact that 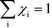 makes it possible to interpret the apparent activation energy as a weighted sum, where only the steps with a finite χi contribute to the apparent activation energy. Elementary steps with χi < 0 are inhibition steps and lower the apparent activation energy. Furthermore, a change in Eapp implies a change in reaction mechanism, since it reflects a change in χ.
makes it possible to interpret the apparent activation energy as a weighted sum, where only the steps with a finite χi contribute to the apparent activation energy. Elementary steps with χi < 0 are inhibition steps and lower the apparent activation energy. Furthermore, a change in Eapp implies a change in reaction mechanism, since it reflects a change in χ.
The expression obtained for Eapp is similar to the one derived in ref. 8. However, as we include entropic effects and pressure, the present result is more general.
4 Analysis of numerical results
In this section, we will investigate the reaction orders and apparent activation energies by analyzing a previously formulated microkinetic model for complete methane oxidation over Pd(100).3 This is done to verify the derived analytical expressions against numerical values.
In ref. 3, we studied complete methane oxidation to CO2 and H2O on Pd, which was modeled in detail using 32 elementary steps. The dominating reaction mechanism was found to depend on the reaction conditions. At high temperatures, the reaction follows a pyrolytic reaction pathway where the main steps are:
| | 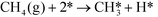 | (R1) |
| | 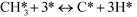 | (R2) |
| | | CO* + O* ↔ CO2(g) + 2* | (R5) |
| | | 2OH* ↔ H2O(g) + O* + * | (R7) |
At low temperatures (R1)–(R7) are augmented by:
| | | COH* + O* ↔ OCOH* + * | (R9) |
In Fig. 1 (top), numerical values of the degree of rate control are shown as a function of temperature over Pd(100). The simulations are performed using the full model in ref. 3. The degree of rate control was obtained by raising the rate constants by 1%. Dissociative methane adsorption (R1) is most rate controlling at all considered temperatures. Additionally, CO formation (R4), COH formation (R8), and oxygen adsorption (R3) exhibit rate-control.
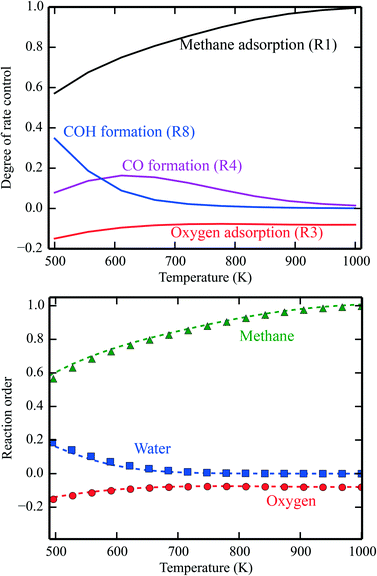 |
| | Fig. 1 Top: Numerical values for the degree of rate control in methane oxidation over Pd(100). The simulations are performed with the full model of ref. 3. Bottom: Reaction orders in the methane, water, and oxygen pressure as a function of temperature. The lines are evaluated by eqn (8), and the points are obtained from the total rate of the full microkinetic model. Pressures: pCH4 = 0.61 mbar, pO2 = 3.06 mbar, and pH2O = 0.01 mbar. | |
In Fig. 1 (bottom), the reaction orders are given as a function of temperature for the reaction over Pd(100). The lines are obtained from the numerical derivative of the rates in eqn (8), and the points are conventional simulations of the reaction order using the total rate. The reaction order for methane varies between 0 at low temperatures and 1 in the limit of high temperatures. This reflects that methane adsorption becomes rate determining in the limit of high temperatures. Thus, the reaction order of methane closely follows χ for methane adsorption. The reaction order in water varies between 0.2 at low temperatures and 0 at higher temperatures. The reaction order in water follows χ for COH formation. COH formation is rate-determining in the limit of low temperatures, and has no rate control at high temperatures. For oxygen, the reaction order is slightly negative in the investigated temperature range. This indicates that oxygen blocks sites on the surface. The reaction order in oxygen follows χ for oxygen adsorption.
The apparent activation energies are shown in Fig. 2, where the symbols are results from microkinetic simulations of the full reaction scheme, obtained by fitting the total rate to eqn (9). The lines are calculated using eqn (19). The blue line is the full expression in eqn (19), whereas the red line excludes the entropy derivative term, and the black line neglects the pressure dependent term. In general, the simulations and analytical values of eqn (19) agree fairly well. The most important contribution to Eapp is the term Ei + kBT. The pressure dependent terms give a significant contribution at the considered conditions, whereas the contributions from the entropy derivatives are small.
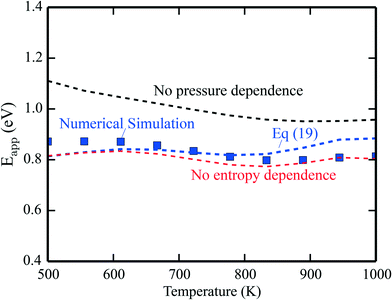 |
| | Fig. 2 Simulated apparent activation energy of complete methane oxidation with the full model of ref. 3 over Pd(100) (blue points). The blue line shows the apparent activation energy evaluated using eqn (19). The red line is eqn (19) excluding or neglecting the entropy derivative and the black line is without the reaction order derivative. Pressures: pCH4 = 0.61 mbar, pO2 = 3.06 mbar, and pH2O = 0.01 mbar. | |
The results obtained using eqn (19) deviate slightly from the simulations. The deviation stems from assuming the Arrhenius form of the rate presented in eqn (9). This form is not expected to be generally compatible with the microscopic kinetics, as the Arrhenius form assumes that the reaction proceeds by one single step, which is an oversimplification as the rate of an elementary step depends on the rates of all the other steps. A single activation energy is therefore insufficient to capture the convoluted microscopic behavior. However, the present analysis, leading to eqn (19), shows which factors enter Eapp, assuming that the rate-law (9) is valid at the microscale. Another example of numerical analysis is given in the ESI† for the reaction under rich conditions.
To further corroborate the results, we analyzed the reaction analytically in two temperature-limits where the quasi-equilibrium approximation holds and analytical formulas can be derived to evaluate the numerical results.
4.1 Analytical results
At high temperatures, dissociative adsorption of methane (R1) is the rate-determining step. Thus, in this case 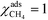 , and only one term enters the reaction order in the methane pressure:
, and only one term enters the reaction order in the methane pressure:| | 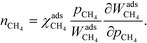 | (20) |
The derivative is found by noting that the number of free sites is not affected by an infinitesimal increase in the methane pressure at the present conditions. This is owing to slow methane adsorption.3 Using this, we obtain the following result:
| | 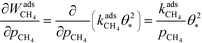 | (21) |
| | 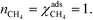 | (22) |
Furthermore, the reaction order in the water pressure is clearly zero as it does not affect the number of free sites. Oxygen has a small negative reaction order, owing to site-blocking for methane adsorption. These results are consistent with the results in Fig. 1 and with our previous observations.3
At low temperatures, the reaction mechanism is slightly different and proceeds through COH and OCOH as intermediates.3 The reaction order in methane is expected to be different as (R8) is the rate-determining step. This step requires OH and C, and the rate can be written as:
The backward rate of this reaction step is negligible. The forward rate constant does not depend on any pressure, and θOH is unaffected by the methane pressure at the present reaction conditions. Hence, the derivative of the carbon coverage determines the derivative of WCOH:
| | 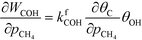 | (24) |
However, this derivative is close to zero as only C and O cover the surface, and C formation is many orders of magnitude slower than oxygen adsorption. Therefore, θC does not change with an infinitesimal change in the pressure, and the reaction order in methane is approximately zero at low temperatures:
The OH coverage affects the reaction, and the reaction order in the water pressure is:
| | 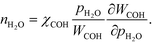 | (26) |
The mechanism for water adsorption (R7) is used to evaluate the derivative. Water transforms into OH via two elementary steps:
Here, the coverages are required to proceed, and we use the fact that each step is equilibrated, which yields:
| | | θH2O = Kaθ*, θ2OH = KbθH2OθO = KaKbθO, | (27) |
where
Ka is the equilibrium constant of
(R11) and
Kb is the equilibrium constant of
(R12). Hence, the coverage of OH is:
| | 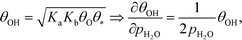 | (28) |
where we assume that the coverages remain unaffected by the infinitesimal change in pressure. Moreover, we assume that
θC is not affected by changing
pH2O. In this case, we obtain:
| | 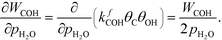 | (29) |
Hence, the analysis predicts:
| | 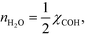 | (30) |
which is the result obtained in the microkinetic model. From this special case, a half reaction order reflects that adsorbing one species produces two of the reactants connected to the rate-determining step.
Oxygen is poisoning the surfaces at all considered reaction conditions, and especially at low temperatures. Therefore, oxygen has a small negative reaction order, and the rate of COH formation is affected negatively by increasing the oxygen pressure:
| | 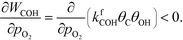 | (31) |
5 Conclusions
In the present paper, reaction orders and apparent activation energies have been related to the degree of rate control (χi). The reaction order is a weighted sum over the elementary step-rates derived with respect to the gas-pressure. Similarly, the apparent activation energy is a sum over the energy barriers for the elementary reaction steps, weighted by χi. The present work provides a microscopic understanding of the reaction order and apparent activation energy, which can be useful in future reaction analyses.
Appendix A – sum rule
As discussed in ref. 14, χi seems to obey a sum rule:| | 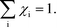 | (32) |
The sum rule is proven by considering a catalytic reaction, where the steady-state catalytic rate is given as the rate of one of the elementary steps ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) :
:
| | 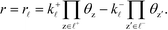 | (33) |
where
k+![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif)
is the forward rate constant,
k−![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif)
is the backward rate constant, and
θz is the coverage of species z. Using the coverage implies that we assume a mean-field picture. The first product in
eqn (33) is taken over z ∈
![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) +
+, which refers to the reactant-species involved in the forward reaction, and z ∈
![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) −
− refers to the reactants of the backward reaction. Changing the forward and backward rate constants corresponds to changing the Gibbs free energy of the transition state,
G‡i, and we let
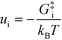
. The definition of
χi is used to obtain the following relation:
| | 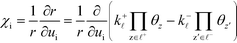 | (34) |
The derivation proceeds by assuming that the coverages are constant for an infinitesimal change in ui. The derivative of the rate constants is:
| | 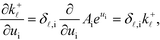 | (35) |
where
δ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) ,i
,i is the Kroneker delta function, and
Ai is the pre-exponential factor. Using this, the sum rule is found to be:
| | 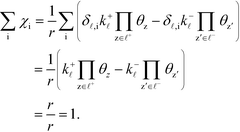 | (36) |
The derivation holds also for catalytic reactions with competing reaction mechanisms, where the rate of the reaction can be written as the sum of the two competing pathways:
| | 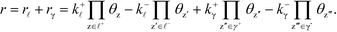 | (37) |
The Kroneker delta functions are again selecting only the terms i = ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) and i = γ. Therefore,
and i = γ. Therefore, 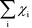 will sum to unity for multiple pathways. It should be noted that problems may arise when there are more than one overall reaction channel and selectivity issues arise.12 This proof of the sum rule might not apply to these situations.
will sum to unity for multiple pathways. It should be noted that problems may arise when there are more than one overall reaction channel and selectivity issues arise.12 This proof of the sum rule might not apply to these situations.
The sum rule for χi was proven in ref. 15 in the case of a three-step reaction. The proof in ref. 15 utilizes the conservation of kinetic sensitivities, which is derived using De Donder relationships.
Conflicts of interest
There are no conflicts of interest to declare.
Acknowledgements
Financial support from the Swedish Research Council and Chalmers Areas of Advance Nanoscience and Nanotechnology and Transport is acknowledged. The calculations were performed at C3SE (Göteborg) and PDC (Stockholm) via a SNIC grant. The Competence Centre for Catalysis (KCK) is hosted by Chalmers University of Technology and is financially supported by the Swedish Energy Agency and the member companies AB Volvo, ECAPS AB, Haldor Topsøe A/S, Scania CV AB, Volvo Car Corporation AB, and Wärtsilä Finland Oy.
References
- C. Campbell, Top. Catal., 1994, 1, 353–366 CrossRef CAS.
- C. J. Heard, C. Hu, M. Skoglundh, D. Creaser and H. Grönbeck, ACS Catal., 2015, 6, 3277–3286 CrossRef.
- M. Jørgensen and H. Grönbeck, ACS Catal., 2016, 6, 6730–6738 CrossRef.
- T. Avanesian and P. Christopher, ACS Catal., 2016, 6, 5268–5272 CrossRef CAS.
- R. Carrasquillo-Flores, J. M. R. Gallo, K. Hahn, J. A. Dumesic and M. Mavrikakis, ChemCatChem, 2013, 5, 3690–3699 CrossRef CAS.
- R. B. Getman and W. F. Schneider, ChemCatChem, 2010, 2, 1450–1460 CrossRef CAS.
- L. C. Grabow, F. Studt, F. Abild-Pedersen, V. Petzold, J. Kleis, T. Bligaard and J. K. Nørskov, Angew. Chem., 2011, 123, 4697–4701 CrossRef.
- H. Meskine, S. Matera, M. Scheffler, K. Reuter and H. Metiu, Surf. Sci., 2009, 603, 1724–1730 CrossRef CAS.
- S. Singh, S. Li, R. Carrasquillo-Flores, A. C. Alba-Rubio, J. A. Dumesic and M. Mavrikakis, AIChE J., 2014, 60, 1303–1319 CrossRef CAS.
- T. L. Wind, H. Falsig, J. Sehested, P. G. Moses and T. T. M. Nguyen, J. Catal., 2016, 342, 105–116 CrossRef CAS.
- C. A. Wolcott, A. J. Medford, F. Studt and C. Campbell, J. Catal., 2015, 330, 197–207 CrossRef CAS.
- C. Campbell, ACS Catal., 2017, 7, 2770–2779 CrossRef CAS.
- H. Eyring, Chem. Rev., 1935, 17, 65–77 CrossRef CAS.
- C. Stegelmann, A. Andreasen and C. T. Campbell, J. Am. Chem. Soc., 2009, 131, 8077–8082 CrossRef CAS PubMed.
- R. D. Cortright and J. A. Dumesic, Adv. Catal., 2001, 46, 161–264 CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Numerical validation of equations in oxygen-poor conditions. See DOI: 10.1039/c7cy01246b |
|
| This journal is © The Royal Society of Chemistry 2017 |
 Open Access Article
Open Access Article * and
Henrik
Grönbeck
* and
Henrik
Grönbeck

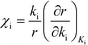
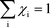 , which is proven in Appendix A. The derived relations provide a clear interpretation of the macroscopic measurables in terms of elementary reaction steps. This is important as reaction orders and apparent activation energies are parameters in phenomenological rate expressions. The relation between global and detailed kinetic parameters should facilitate the understanding and development of catalytic processes.
, which is proven in Appendix A. The derived relations provide a clear interpretation of the macroscopic measurables in terms of elementary reaction steps. This is important as reaction orders and apparent activation energies are parameters in phenomenological rate expressions. The relation between global and detailed kinetic parameters should facilitate the understanding and development of catalytic processes.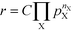
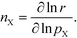
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) pX,
pX,![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Gj)]].
Gj)]].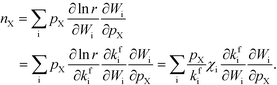
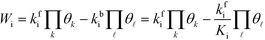
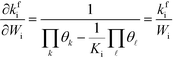
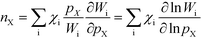
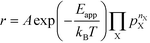
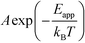 is known as the rate constant of the reaction (k). In general, it is not clear if a rate-law such as eqn (9) can fully describe the reaction. However, assuming that it is valid, it is interesting to analyze what factors contribute to the apparent activation energy.
is known as the rate constant of the reaction (k). In general, it is not clear if a rate-law such as eqn (9) can fully describe the reaction. However, assuming that it is valid, it is interesting to analyze what factors contribute to the apparent activation energy.
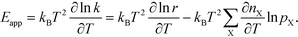
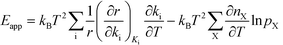
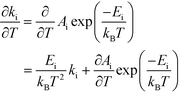
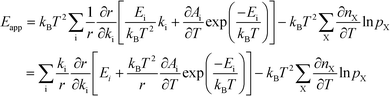
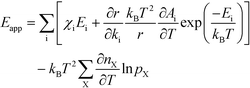
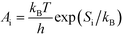
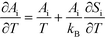
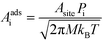
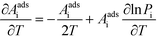
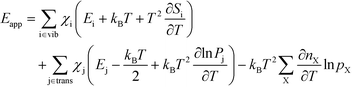
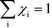 makes it possible to interpret the apparent activation energy as a weighted sum, where only the steps with a finite χi contribute to the apparent activation energy. Elementary steps with χi < 0 are inhibition steps and lower the apparent activation energy. Furthermore, a change in Eapp implies a change in reaction mechanism, since it reflects a change in χ.
makes it possible to interpret the apparent activation energy as a weighted sum, where only the steps with a finite χi contribute to the apparent activation energy. Elementary steps with χi < 0 are inhibition steps and lower the apparent activation energy. Furthermore, a change in Eapp implies a change in reaction mechanism, since it reflects a change in χ.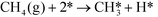
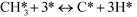


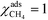 , and only one term enters the reaction order in the methane pressure:
, and only one term enters the reaction order in the methane pressure: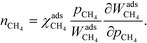

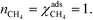
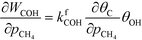
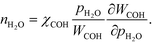
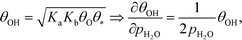
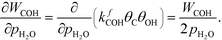
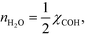
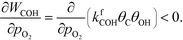
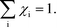
![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) :
: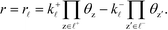
![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) is the forward rate constant, k−
is the forward rate constant, k−![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) is the backward rate constant, and θz is the coverage of species z. Using the coverage implies that we assume a mean-field picture. The first product in eqn (33) is taken over z ∈
is the backward rate constant, and θz is the coverage of species z. Using the coverage implies that we assume a mean-field picture. The first product in eqn (33) is taken over z ∈ ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) +, which refers to the reactant-species involved in the forward reaction, and z ∈
+, which refers to the reactant-species involved in the forward reaction, and z ∈ ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) − refers to the reactants of the backward reaction. Changing the forward and backward rate constants corresponds to changing the Gibbs free energy of the transition state, G‡i, and we let
− refers to the reactants of the backward reaction. Changing the forward and backward rate constants corresponds to changing the Gibbs free energy of the transition state, G‡i, and we let 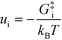 . The definition of χi is used to obtain the following relation:
. The definition of χi is used to obtain the following relation: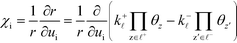
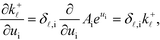
![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) ,i is the Kroneker delta function, and Ai is the pre-exponential factor. Using this, the sum rule is found to be:
,i is the Kroneker delta function, and Ai is the pre-exponential factor. Using this, the sum rule is found to be: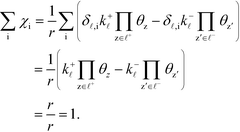
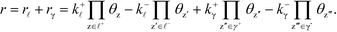
![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) and i = γ. Therefore,
and i = γ. Therefore, 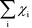 will sum to unity for multiple pathways. It should be noted that problems may arise when there are more than one overall reaction channel and selectivity issues arise.12 This proof of the sum rule might not apply to these situations.
will sum to unity for multiple pathways. It should be noted that problems may arise when there are more than one overall reaction channel and selectivity issues arise.12 This proof of the sum rule might not apply to these situations.