Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Forty years of temporal analysis of products
K.
Morgan
 *a,
N.
Maguire
a,
R.
Fushimi
*a,
N.
Maguire
a,
R.
Fushimi
 b,
J. T.
Gleaves
c,
A.
Goguet
a,
M. P.
Harold
b,
J. T.
Gleaves
c,
A.
Goguet
a,
M. P.
Harold
 d,
E. V.
Kondratenko
e,
U.
Menon
d,
Y.
Schuurman
d,
E. V.
Kondratenko
e,
U.
Menon
d,
Y.
Schuurman
 f and
G. S.
Yablonsky
g
f and
G. S.
Yablonsky
g
aSchool of Chemistry and Chemical Engineering, Queen's University Belfast, Belfast BT9 5AG, UK. E-mail: kmorgan08@qub.ac.uk
bIdaho National Laboratory, Idaho Falls, Idaho ID 83415, USA
cDepartment of Energy, Environmental and Chemical Engineering, Washington University, St Louis, Missouri MO 63130, USA
dDepartment of Chemical and Biomolecular Engineering, University of Houston, Houston, Texas TX 77204-4004, USA
eLeibniz-Institut für Katalyse e.V. an der Universität Rostock, Rostock, D-18059, Germany
fIRCELYON, Université Claude Bernard Lyon 1, Villeurbanne Cédex, F-69626, France
gParks College of Engineering, Aviation and Technology, Saint Louis University, Saint Louis, Missouri MO 63103, USA
First published on 16th May 2017
Abstract
A detailed understanding of reaction mechanisms and kinetics is required in order to develop and optimize catalysts and catalytic processes. While steady-state investigations are known to give a global view of the catalytic system, transient studies are invaluable since they can provide more comprehensive insight into elementary steps. For almost forty years temporal analysis of products (TAP) has been successfully utilized for transient studies of gas phase heterogeneous reactions, and there have been a number of advances in instrumentation and numerical modeling methods in that time. Since TAP is a complex methodology it is often viewed as a niche specialty. With the purpose to make TAP more relevant and approachable to a wider segment of the catalytic research community, part of the intention of this work is to highlight the significant contributions TAP has made to elucidating mechanistic and kinetic aspects of complex, multi-step heterogeneous reactions. With this in mind, an outlook is also disclosed for the technique in terms of what is needed to revitalize the field and make it more applicable to the recent advances in catalyst characterization (e.g. operando modes).
1 Introduction: catalysis and the need for catalyst characterization
Catalysis is economically and environmentally important for the chemical industry, and is involved in the processes for up to 80%1,2 of products from all industrial sectors (such as polymers, pharmaceuticals, agrochemicals, petrochemicals, environmental clean-up and emission control). Catalysts affect the kinetics of chemical reactions and thus improve conversion and/or selectivity of processes, and can also reduce operating temperature and/or pressure, which is important with respect to system maintenances and environmental protection.1–4Industrial catalysts are typically multi-component solids which are often seen as a mystery box, and so developing a catalyst with the optimal chemical and physical characteristics to operate in an industrial process often requires years of research and development.4–6 Ultimately, an optimized catalyst will have the best compromise between conversion, selectivity, mildest reaction conditions, stability and lifetime.6 At every stage of catalyst research and development, kinetic experiments are essential to establishing the desired chemical and physical properties.6 To develop such catalysts, a good understanding of the catalyst surface phenomena in terms of individual reaction pathways and their relationships with material properties is required.7,8
The lack of detailed understanding of the catalytic processes can oftentimes lead to undesirable and expensive outcomes. An example of such a situation is in automotive catalysis where the catalysts contain excessive metal loadings to ensure that the catalyst remains effective beyond its guaranteed lifetime due to environmental legislation.9,10 With increased industrialization and stricter emission legislation, the demands on precious metal resources are ever-growing10,11 and therefore it is even more important for optimized catalysts to be developed.
1.1 Steady-state versus transient kinetic studies
The normal procedure for testing the performance of industrial catalysts makes use of what is known as steady-state conditions. The steady-state experiment regime is defined as having constant temperature, flow rate, partial and total pressures at the reactor inlet. Types of steady-state technique used for kinetic studies include plug flow (PFR) and continuously stirred tank (CSTR) reactors12,13 Typical steady-state experiments can only provide the “global behaviour” of catalysts due to the low time resolution, a consequence of their simple design.8 It is not straightforward to use the apparent kinetics gained from steady-state analysis to further the knowledge of elementary catalytic steps.7Transient kinetic studies are an alternative method that is based upon the rapid changing of one of the reaction variables (temperature, flow rate, pressure or concentrations).8,14–16 This induces a perturbation in the system and then the time dependence of the relaxation/response of the system is monitored. With higher time resolution, transient kinetics can provide an insight into the reaction mechanism including short-lived intermediate species that are typically not accessible through steady-state studies.7 A further application of transient kinetics is the provision of rate constants for elementary steps of the process.17 One of the most successful techniques that have been employed in transient kinetic studies is the temporal analysis of products (TAP) reactor.14 The TAP reactor system is a fully automated research instrument designed to perform kinetic experiments at temperatures up to 1000 °C5 on a variety of materials ranging from single metal particles18 to complex multi-component solids.5
With a view to bringing this technique to a wider audience, including newcomers to this field, the current work is designed to highlight the achievements of TAP, its most recent developments as well as to discuss some aspirations for the future. The analytical mathematical models for the TAP methodology are extensively discussed in the literature,16,19 so only specific aspects are discussed in section 4 of the current document.
2 The temporal analysis of products methodology
2.1 A conceptual basis
The TAP approach14 was proposed by John T. Gleaves forty years ago, with its origins being as a combination of two methodologies:• Molecular beam methodology developed by Dudley Herschbach and Yuan T. Lee.20
• Relaxation methodology proposed by Manfred Eigen in the 1950s21 for studying transient regimes. This also sparked an interest in relaxation studies in heterogeneous catalysis.22,23
More specifically, the use of molecular beam scattering experiments using single crystals24,25 and methods used to study the rates and mechanism of very low pressure pyrolysis26 formed a conceptual basis for a novel pulse response method, from which a corresponding apparatus (TAP-reactor) was created, of which the original schematic is reported in Fig. 1.27
 | ||
| Fig. 1 Schematic of TAP system which appeared in original research proposal in 1977 by J. T. Gleaves.27 | ||
Early in the development of the TAP experiment, an idea evolved that collisions between probe molecules and a complex solid may provide a unique kinetic signature contained in the motions of the scattered molecules.28 It was supposed that this signature would be a characteristic of the composition and structure of the catalyst surface. This idea was supported by results obtained in surface science experiments involving small molecules and metal single crystals.14,29
The TAP vacuum pulse response experiment was designed to capture key features of a molecular beam scattering experiment. An important goal was to create a tool with an extreme sensitivity to changes in surface composition and structure induced by reaction.28
The experimental focus was to attain maximum time resolution and product sensitivity, while controlling the number of gas–solid collisions and limiting the number of gas-phase collisions. The simple idea was to replace the molecular beam target with a reaction zone that contained the solid sample. The sample could be in the form of a single pellet, coated on the walls of the reaction zone, deposited on metal screen or quartz wool, or in the form of a packed bed. Like a molecular beam experiment the reaction zone would be in a vacuum chamber, probe molecules would be introduced in short pulses to extract the time dependence of the different physical and chemical processes and the reaction zone exit flow would be monitored by a mass spectrometer (MS).14 Some of the original results from the 1st generation TAP, obtained with a chart recorder, are reported in Fig. 2.30
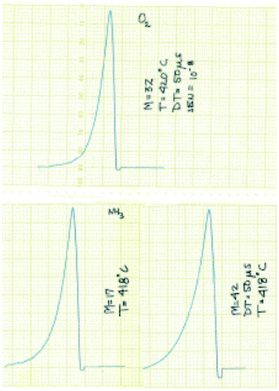 | ||
| Fig. 2 Original TAP pulse responses for O2, NH3 and C3H6 over SiO2 obtained with a chart recorder.30 The pulses are plotted from right to left and the scale is 1 cm equal to 0.5 s. | ||
The 2nd generation TAP incorporated a computer for data acquisition, and the first comprehensive paper on the TAP experiment, which described this quantitative apparatus, was published in 1988.14 The development of the 3rd generation TAP as a commercial unit, known as TAP-1, began in 1986 in conjunction with Autoclave Engineers, a prototype of which was completed in 1987. The TAP-1 was the first system to employ computer control of pulse valve operation, reactor temperature programming and data acquisition. In 1992, a movable sealing assembly was developed allowing the TAP-1 micro-reactor to be cycled between atmospheric pressures and vacuum conditions. With this modification, the TAP reactor system could perform steady-flow, pulse response, and step transient experiments at higher pressures.
Development of the TAP-2 system began in 1994 and involved redesign of the TAP vacuum system and pulse valve manifold. The key difference between the TAP-1 and TAP-2 systems is the positioning of the microreactor relative to the ionizer of the MS. In the TAP-2 system, the reactor exit is physically much closer to the ionizer, and as result its detection efficiency is ≈2 orders of magnitude higher than in the TAP-1 system.
Current commercial versions of the TAP reactor system retain the same basic vacuum system design as the TAP-2 system. Recent developments in TAP hardware include a high-pressure pulse valve manifold and reactor assembly that allows transient experiments to be performed at pressures exceeding 100 bar. The second comprehensive paper on the TAP experiment was published in 1997 and contains a detailed description of the TAP-2 reactor system, and also introduced the “interrogative kinetics” research methodology.7
2.2 The TAP Knudsen pulse response experiment
Key components of TAP pulse response experiments include:8• A pulse valve or valve manifold for delivering single pulses, or pulse sequences.
• A temperature controlled microreactor.
• A MS enclosed in an ultra-high vacuum (UHV) chamber.
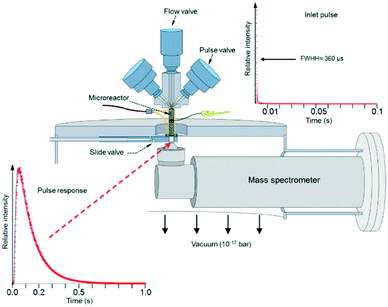
Fig. 3 depicts the basic TAP-2 configuration in which the outlet of the microreactor is sealed against the vacuum chamber and positioned directly above the ionizer of the MS.
There are several different operating modes of the TAP reactor (see section 2.4), but the most basic experiment is a single pulse experiment. A small amount of gas (1013–1015 molecules) is pulsed at the reactor inlet. This will lead to a pressure in the reactor between 2 × 10−6 and 2 × 10−4 bar.28,31 In this pressure range, for a reactor packed with catalyst particles with a diameter below 200 μm, the mean free path of the molecules will be longer than the distance between two particles.31 Under such conditions, intermolecular collisions are negligible. This corresponds to the Knudsen diffusion regime7,14,32 (eqn (1))5 which is a well-defined transport mechanism where diffusion is dependent on temperature and molecular weight. This is completely different than that encountered in conventional flow reactors, where both convection and diffusion occur, such as Brownian diffusion where molecular motion is partly a consequence of molecular collisions.
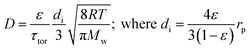 | (1) |
The diffusivity (D) of Knudsen diffusion; ε is the fractional bed voidage, di is internal diameter of channels between particles, τtor is tortuosity, R is the universal gas constant, T is the temperature (K), Mw is molecular weight and rp is the radius of the particles.
The plot displayed in the lower left part of Fig. 3 is an example of a Knudsen pulse response curve. The corresponding inlet pulse is shown in the upper right corner of Fig. 3. For comparison, the two plots are height normalized to underscore the difference in time dependence. An important characteristic of an inert gas Knudsen pulse response curve is that its contour is not determined by the intensity of the inlet pulse.5,17,33 There exists a range of inlet pulse intensities with an upper limit but no lower limit that will produce a Knudsen response. In this regime, the pulse intensities decrease but the time dependencies of the response curves are identical. At higher intensities the response curves display complex time dependence and the curve shapes evolve as the inlet pulse intensity increases.
In the Knudsen regime, an inert gas pulse response is shaped by three factors:5
• The molecular mass of the injected species.
• The catalyst bed temperature.
• The nature of the bed void space, which is determined by the size, shape and packing of particles in the microreactor.
In a Knudsen pulse response experiment, all gas phase species move randomly through the particle bed, independent of one another, at a speed determined by their mass and the bed temperature.34 The void space determines the structure of the particle maze that a molecule must navigate before travelling into the MS chamber. If an inert gas is mixed with other gases, the pulse response of the inert can be used to determine if the mixture is operating in the Knudsen regime.5 With the particles bed temperature constant, decreasing the pulse intensity and verifying that the normalized pulse shape of the inert remains the same, confirms Knudsen behaviour.5,17,33
2.3 The relevance of TAP experiments
In the forty year history of the TAP-approach, different aspects have been developed, including:• Kinetic characterization of heterogeneous catalysts based on mathematical theory.5,7,8
• Deciphering of mechanisms of complex catalytic reactions5,7,8,28
• Revelations of “composition–activity” and “structure–activity” relationships. In particular, an analysis of structures arising in the course of complex catalytic reaction (‘emergent structures’).28
Illustration of the type of studies and results that can be obtained regarding these three aspects is provided in the form of case studies in section 3.
The type of material used in surface science studies (model catalysts) typically differs from those for industrial applications (multi-component catalyst). This is often referred to as the material gap.35 In contrast, TAP can use a range of catalyst material types, from model to practical catalysts, to study mechanisms, kinetics and transport phenomena in heterogeneous catalysis at temperatures up to 1000 °C.5,28,36–40
The pressure gap is defined as the difference in the pressure experienced by a catalyst under real-life environments compared to when studied using surface science techniques.41 In contrast to UHV surface science techniques used for elucidating reactions on a near-to elementary level, the TAP reactor operates at higher pressures. Although the MS chamber is at UHV conditions and the exit flow from the microreactor is exposed to UHV, the gases are introduced to the microreactor at higher pressures, and the later experiences a pressure gradient across it. TAP can also operate at higher pressures in a flow mode, thereby allowing the same sample, in the same sample environment (microreactor), to be studied over a wider range of conditions, from UHV up to and above ambient pressures. Therefore, TAP can operate over a pressure range that is neither typical of surface science or operando conditions, but in between these extremes, thus “bridging the pressure gap” with respect to industrial conditions, i.e. “accesses different pressure regimes” from UHV up to ambient and higher pressures.42 The ability of TAP to bridge the pressure gap is a key aspect in terms of the relevance of any kinetics obtained from TAP experiments. The similarities and complimentary aspects of standard TAP experiments and high-pressure TAP are summarized in Fig. 4.
The relevance of TAP data to “real-life” behaviour of catalyst is a key point and while care should always be applied to cross-validate using complimentary experiments, several studies have reported results which bring confidence in supporting such relevance. For instance, TAP has been used to quantify the number of active sites present on catalysts,36 and these were found to be in agreement with previously published steady-state isotopic transient kinetic analysis diffuse reflectance infrared Fourier transform spectroscopy (SSITKA DRIFTS) results.43
Other examples of correlation/complementation of TAP experiments with other methods include electron paramagnetic resonance (EPR) spectroscopy,44,45 X-ray photoelectron spectroscopy (XPS),44,46,47 X-ray diffraction (XRD),44,46,48 X-ray absorption spectroscopy (XAS),44,47 Raman,46 energy dispersive X-ray scanning transmission electron microscopy (EDX-STEM),46 high angle annular dark field scanning transmission electron microscopy (HAADF-STEM),48,49 Fourier transfer Infrared (FTIR),49 high resolution scanning transmission electron microscopy (HRTEM)47,50,51 and prompt gamma-ray activation analysis (PGAA).52 As such, while many reports have been dedicated solely to TAP, it should be noted that TAP is not a necessarily standalone characterization technique and can/should be used in a complimentary way with other methodologies.
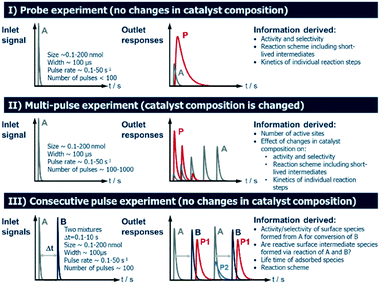
2.4 Operating modes of TAP Knudsen pulse experiments
Several operating modes are accessible to the TAP reactor and these are summarized in Fig. 5 together with their specific features.7 The single pulse (probe) (see section 2.4.1) and multi-pulse (see section 2.4.2) modes of operation can be used to determine the sequence of reaction steps involved, the diffusion of reacting species from the catalyst lattice, the influence of different surface concentrations on the rate of surface processes and the number of catalytically active sites. These two modes are also known as state-defining and state-altering experiments, respectively.7 The combination of these two types of experiment is collectively known as interrogative kinetics.7Another mode of operation is known as the sequential/consecutive pulse or pump–probe method (see section 2.4.3). It utilizes a sequence of pulses of reactant molecules with one reactant pulsed from one valve into the reactor at t = 0, while the second reactant species is introduced from another valve at t = x (where x is a time delay which is varied over a number of time intervals).
The interactions between the adsorbing molecules and the catalyst can be characterized quantitatively in terms of adsorption/desorption properties.15 To do so, the measured average residence time of the adsorbing molecule is compared to the theoretical average Knudsen diffusional residence time for the same molecule. The average Knudsen diffusional residence time is easily calculated from the average residence time of the inert reference gas and the known proportional trend of Knudsen diffusion on molecular weight and temperature.17 Thus, the change in the average residence time due to the mass dependency of the diffusion velocity of molecules with different molar masses is taken into account.17
It is important to note that this approach has several restrictions.17
• First, the adsorption process must be completely reversible within the investigated conditions.17 This can be verified by checking for complete detection of the pulsed amount of reactants within the response. The lower temperature limit, above which this approach can be used, is determined by the limit in response pulse broadening beyond which a complete detection of the pulsed molecules can no longer be accurately obtained.17 The upper temperature limit is usually defined by the onset of chemical reactions, which, in turn, change the pulse response.17
• Second, the pulse size must be limited to ensure that the mass transport only occurs by Knudsen diffusion.17
Information on the catalytic performance in terms of conversions and yields is obtained using the integral size of the pulse responses of reactant and products. The constant size and shape of the inert reference gas response ensures that the dosed amount of reactant does not change during the experiment. Due to the high time resolution of the TAP technique (due to the sharp inlet pulse and fast transport58), it is possible to use normalized versions of the pulse responses for the different products to obtain information on the sequence of formation of the different products. This is derived from the fact that the formation of a reaction product requires a certain period of time for each reaction step to occur. The pulse responses of secondary products, therefore, are delayed in comparison to those of primary products, while components formed during the same reaction step appear simultaneously. It is important to note that such analysis is only valid if the time for the diffusive mass transport is (much) smaller than the time required for reaction, if the desorption of products into the gas phase is a fast process and if the surface reactions are virtually irreversible.17
Pulse experiments can also be applied to determine the effective Knudsen diffusion coefficient within fixed beds and wash-coated monoliths.17,60 For this purpose, the average residence time for small, single pulses of non-adsorbing gases (less than 2 × 1015 molecules) within the isothermal fixed bed reactor is measured.17
The correlation between the changes in catalytic properties and the changes in catalyst state (bulk, surface composition, and oxidation state) provides information to develop activity–structure or activity–composition relationships, and help constructing models of the active catalytic site. It is also important to note that this progressive consumption of a pre-loaded/adsorbed reactant will allow the obtaining of information regarding the number of adsorption sites and kinetics characteristics of these sites.17,36 In contrast to the single pulse experiments, these pulse experiments are not restricted to Knudsen diffusion conditions and can use large pulses (i.e. higher pressure pulses). However, in general, Knudsen diffusion conditions are used to access the maximum of kinetic information. Multi-pulse experiments are also instrumental in quantifying the concentration of active sites. To this end, various probe molecules are used. In comparison with classical pulse methods, the TAP technique is perfectly suitable for titration experiments using catalysts with amounts of active sites, i.e. approximately 1016 sites per catalyst gram,60,61 since titration experiments can be performed with a pulse size lower than 1 × 1014 molecules. This allows for a “state by state” transient screening due to insignificant perturbation of the catalyst composition from pulse to pulse, given that the number of molecules in each pulse is less than 1% of the total number of active sites.65
Consecutive pulse experiments have proven to be very effective in determining lifetime of intermediates68–70 while providing detailed mechanistic insights.37,71 Information about the lifetime and the amount of the surface intermediate can be derived from the product yields as a function of the offset time between the pulses of the two reactants and their pulse size. This allows the studying of processes that involve rapid changes in the concentration of a reactive surface species. The use of isotopes can help distinguish between mechanistic routes that produce the same product. The pump–probe format can also be used to distinguish processes that involve bulk diffusion from surface processes, and can provide information on the reactive formation of catalytic sites.17
2.5 Other types of TAP operating mode
While the single, multi and consecutive pulses correspond to the majority of TAP experiments, there are additional types that are worthy of interest. The application of continuous gas feed allows for the use of larger amounts of reactants which in turn will lead to more pronounced changes in the state of the catalyst. For instance, in situ activation of a catalyst under atmospheric pressure within the TAP reactor may be required to obtain relevant information on catalysts with pre-defined initial state (e.g. fully oxidized, fully reduced). These experiments can be conducted thanks to the gate valve (referred to as a slide valve in newer instruments or a high-pressure assembly in TAP-1 instruments) that allows isolation of the reactor from the high vacuum chamber, while the reaction taking place can be monitored via a “bleed” valve to the MS located at the outlet of the reactor. “High-pressure” mode experiments have been utilized and compared at vacuum and atmospheric pressures.72Similar types of information can be obtained using long series of very large pulses. The time window for the investigated processes addressed, however, is shifted to longer durations compared to typical TAP experiments. A few investigations have reported the use of TAP set-ups in temperature programmed (TP) applications, such as desorption (TPD), surface reaction (TPSR), oxidation (TPO), or reduction (TPR).73,74 The use of a TPD mode is advantageous since it allows the characterization of adsorbates on the catalyst. In the case of strong adsorption, the use of pulse experiments will probe the adsorption of reactants, while the temperature programmed studies will provide information on the thermal stability of adsorbed intermediates in different atmospheres. One example of such approach is the study by Dewaele and Froment on the adsorption of CO and CO2 on alumina.73
The use of isotopes is helpful (and sometimes indispensable) and, per se, not a different type of TAP experiment but a desirable complementation of the more standard experiments using non-labelled reactants to unravel reaction mechanism. Isotopically labelled molecules are expensive which greatly limits their use. In this respect, the TAP reactor is an ideal tool for their implementation since the amount of reactant needed is small.61 A typical context where isotopically labelled reactant can be used is the clarification of the involvement of bulk/dissolved or lattice atoms when a Mars–van Krevelen mechanism is suspected.71 In this case, the catalyst is pre-treated using one isotope of the reactant under investigation, e.g.16O2, and the experiments are carried out using another isotope of this reactant, e.g.18O2. The time dependence of the isotopic distribution within the products will give information about the reaction mechanism. Another context where the use of isotopes will be helpful concerns the identification of products in a mass spectrum. Different molecules will give contribution to the same mass and the deconvolution of mass spectra can be difficult. A typical example is the deconvolution of CO and N2, both having their principal mass contribution at 28. The use of 15N or 13C as the source of nitrogen or carbon increases the mass by one (15N16O = 29 or 13C16O = 29) and therefore deconvolution is no longer necessary.
Table 1 highlights a number of references from the literature that use the TAP reactor modes of operation, and summarizes some of the information derived from these studies.
| Experiment | Information | Ref. |
|---|---|---|
| Single-pulse technique | Diffusivities | 14, 53–60 |
| Adsorption/desorption properties | ||
| Product formation sequence | ||
| Number of adsorption sites | ||
| Elucidation of reaction pathways | ||
| Consecutive pulse technique flow experiment | Lifetime of surface intermediates | 17, 56, 66, 67 |
| Elucidation of reaction pathways | ||
| Role of catalyst bulk-dissolved and lattice species in the reaction | ||
| Temperature-programmed desorption (TPD), reaction (TPSR) | Thermal stability of intermediates | 73, 74 |
| Redox properties of solid oxide catalysts |
3 Exemplar applications of the TAP reactor
This section is intended to illustrate the flexibility and versatility of the TAP methodology in various situations relevant to the deciphering of complex mechanisms, kinetic characterization and “structure–activity” relationships. Generally, publications from the time period of 2007–2016 are discussed. For a summary of TAP studies prior to 2007 the reader is referred to the literature.7 There is no overall discussion or cross comparison of the subsections as this would not be appropriate due to the intended diverse nature.3.1 Mechanistic studies
In comparison to other kinetic analysis tools, the high time-resolution of the TAP technique presents a key advantage for discriminating the details of a reaction mechanism: from simple adsorption mechanisms to more complex multi-step surface mechanisms. In the following section, key TAP results for elucidating reaction mechanisms are presented for different materials and chemistries.3.1.1.1 Mars–van Krevelen mechanism. Numerous TAP studies of CO oxidation on different materials (Au/TiO2, nanoporous gold, etc.) have been published and generally the Mars–van Krevelen mechanism is indicated.71,75–78 Isotope pulsing is a simple method to quickly distinguish the role of lattice oxygen. As indicated in section 2.5, in this type of experiment the catalyst is typically oxidized using 16O2 and the reductant is pulsed (simultaneously or in a pump–probe fashion) with 18O2. If the lattice oxygen is the key oxidizing species then initially only 16O will be incorporated into the products. As 16O is depleted and pulsed oxygen replenishes, 18O containing products slowly emerge. Some examples where this approach was used include: CO oxidation,71,76 propane total oxidation,79,80 toluene oxidation,81 selective oxidation62 and oxidative dehydrogenation.82 Alternatively, the reoxidation step may be reversible and isotopic exchange with the lattice may be observed by pulsing 18O2 to detect 16O18O and 16O2 in the oxygen pulse response; for example this method was utilized in the study of diesel soot oxidation.83
Anaerobic pulsing of the reductant is another method for detecting the role of lattice oxygen. In this case the oxidized material is exposed to reductant pulses with no oxygen input and the selectivity is monitored. If the pulsing is discontinued and the material is held in vacuum at high temperature this can lead to a resupply of oxygen to the surface by diffusion from the bulk. Upon restarting the reductant pulsing, an increase in selective products will be observed if their formation proceeds via Mars–van Krevelen mechanism. Researchers have also used separate alternating multi-pulse series of reductant and oxidant to probe the adsorption/reaction mechanism. Examples where anaerobic pulsing methodologies have been used to indicate Mars–van Krevelen mechanism include: propane total oxidation,80 toluene oxidation,81,84,85 CO oxidation,71,75–77,86,87 ammonia oxidation,88 oxidative coupling of methane,61,89 oxidative dehydrogenation of alkanes62,82,90,91 and partial oxidation of methane.92
3.1.1.2 Langmuir–Hinshelwood mechanism. The pump–probe experimental mode is particularly useful for distinguishing a Mars–van Krevelen mechanism from that of a Langmuir–Hinshelwood. For example, in a study of HCl oxidation (Deacon chemistry) the Cl2 pulse response was monitored when oxygen and HCl pulses were separated with varying time delays. For MnO2, Cr2O3 and CeO2 catalysts the intensity of Cl2 production upon HCl injection was independent of the delay time between O2 and HCl indicating the participation of stable lattice oxygen species. However, in the case of RuO2 a progressive decrease in the Cl2 production with increasing time delay was found indicating a strong dependence on oxygen coverage and a Langmuir–Hinshelwood type mechanism for this material.93–96
Similar experiments, in the pump–probe mode, were used to distinguish a competitive adsorption mechanism for CO oxidation over a supported gold catalyst.97 Generally, (see references in section 3.1.1.1) participation of the lattice oxygen is observed for this chemistry on gold. From CO/O2 pump–probe experiments Olea et al. observed a maximum in the CO2 yield as a function of the time delay between CO and O2 which indicates the role of pre-adsorbed oxygen in the reaction. If lattice oxygen were participating there should be no time delay-dependence for CO2 production (in addition, isotopic measurements also did not indicate participation of lattice oxygen).97
3.2 Kinetic studies
Owing to its unique technical characteristics, the TAP reactor system has often been applied for unravelling the kinetics of individual reaction pathways in the course of various multi-step heterogeneous reactions.8 Kinetic data are extracted from outlet transient responses of feed components and reaction products. This section discusses kinetic studies after 2007, since preceding publications have been described previously.8,108 In comparison with steady-state approaches, kinetic models for TAP experiments consist of differential equations accounting for both temporal and spatial changes in the concentration of reaction participants. In addition, a pseudo steady-state concentration for surface intermediates is not valid thus the rate equations are given in terms of individual, near-to elementary steps. When evaluating TAP experiments kinetically, both mass transport and chemical processes are taken into account. The latter process occurs exclusively in the catalyst zone, whereas feed components and reaction products diffuse through all three zones or two zones (catalyst zone and downstream inert zone), respectively. For TAP experiments with a pulse size below 1015 molecules, mass transport can be quantitatively described by Knudsen flow.The Y-procedure, which is briefly discussed in section 4.2.1 enables the extraction of chemical transformation rates from reaction–diffusion data with no assumption on the kinetic model, which can be applied to TAP experiments performed in a thin zone tap reactor (TZTR)118 configuration and moment based analysis approach to minimize macroscopic concentration non-uniformity in the microreactor.5,119
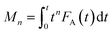 | (2) |
Calculation of moments where FA(t) is the exit flow, molecules s−1 or s−1 (normalized exit flow); M0 is the zeroth moment (n = 0), i.e. the area under the curve, molecules or dimensionless (normalized); M1 is the first moment (n = 1), molecules s, or s (normalized); M2 is the second moment (n = 2), molecules s2, or s2 (normalized).
For a simple first order reaction, apparent rate constants can be obtained from M0 (conversion degree) of the feed component response and gas residence time in the catalyst zone.33 As stated previously, higher moments (M1 and M2) are used for determining other primary kinetic coefficients.33 Herein, the results of selected TAP studies aimed at deriving kinetic parameters are discussed. Table 2 summarizes reactions and catalysts studied, kinetic models used and type of reaction parameters derived.38,63,71,108,110,114,120–124 The kinetics of CO adsorption and oxidation have been studied,40,71,120 using the TZTR approach. The main focus was put on the role of supported metals (Au or Pt) and the kind of active oxygen species on performance of Au/SiO2, Pt/CeO2, CuMnOx and Au/CuMnOx. Irrespective of catalyst composition, CO adsorbs reversibly and reacts on the surface of catalysts with adsorbed oxygen species. Only one kind of oxygen species was determined to be responsible for CO2 formation over CuMnOx, while an additional oxygen species originated from gas-phase O2 upon adsorption on supported metals participated in the target reaction over other catalysts. The latter species showed, however, lower activity. Although no experimental evidences were provided it was suggested that low-active oxygen species on Au/SiO2 is one dissolved in the volume of Au nanoparticles.120
| Catalysts | Near to elementary reaction steps | Kinetic parameters | Ref. |
|---|---|---|---|
| CO oxidation | |||
| Pt/CeO2 | CO+ * ⇆ *–CO *–CO → intermediates | Constants and activation energies of individual reaction steps number of active sites | 38 |
| Pt/SiO2 | CO+ * ⇆ *–CO CO + *–O → CO2 | Equilibrium constant of CO adsorption, constant of CO oxidation | 120 |
| CuMnOx Au/CuMnOx | O2 + * ⇆ *–O2 *–O2 + * → intermediate CO+ * ⇆ *–CO *–CO + *–O → *–CO2 | Constants of individual reaction steps | 71 |
| C3H8 dehydrogenation | |||
| Pt–Sn–K/γ-Al2O3 | C3H8+ * → x*–H + *–C3H8−x | Constant and activation energy | 121 |
| VOx/TiO2 | C3H8 + 2*–O → *–OH + *–O C3H7 C3H8 + 2*–O → *–OH + *–OCH(CH3)2 C3H6 + 2*–O → *–OC2H4 + *–OCH2 *–OOCH + *–O → CO2 +*–OH + 2* | Constants and activation energies of individual reaction steps | 123 |
| NH3 oxidation | |||
| Pt wire, Pt/α-Al2O3, Pt/CeO2–TiO2, CeO2 | NH3 + *–O → products | Constant of NH3 activation | 122 |
| Partial oxidation of methane | |||
| Rh/Al2O3 | O2 + * ⇆ *–O2 CO2 + * → *–CO2 *–CO2 + * → *–CO + *–O CH4 + *–O → products CH4 + * → products | Constants of individual reaction steps | 63 |
The TZTR approach has also been applied for determining the apparent rate constant of NO formation upon NH3 oxidation over Pt wire, Pt/α-Al2O3, Pt/γ-Al2O3, Pt/CeO2–TiO2, CeO2–TiO2.121 The lowest constant was obtained for NO formation over unloaded CeO2–TiO2, where lattice oxygen of CeO2 was the active species. Adsorbed oxygen species formed from gas-phase O2 on Pt (Pt wire, Pt/α-Al2O3, Pt/γ-Al2O3) showed higher activity as concluded from the apparent rate constant. A significantly higher apparent rate constant was estimated for NO formation over Pt/CeO2–TiO2. This was related to a synergy effect between the noble metal and the support to provide adsorbed and lattice oxygen species for selective NH3 oxidation in a complementary fashion.
With the purpose to compare different approaches, Lobera et al.121 applied the moment approach for non-thin and TZTR as well as numerical solution for deriving kinetics of non-oxidative propane dehydrogenation over Pt–Sn–K/γ-Al2O3. A simple model assuming the irreversible breaking of a C–H bond in propane was used. The obtained apparent rate constant and corresponding activation energy did not significantly depend on the calculation method. This result was, however, expected because in all approaches the degree of propane conversion was used for determining the kinetic parameters. More complex reactions with several gas phase species and surface intermediates should be selected for proper comparison of different methods for kinetic evaluation of TAP data. Unfortunately, the moment based approaches have been limited to rather simple reactions. As a consequence, despite the fact that kinetic schemes have to be pre-defined for numerical methods, the latter are workhorses in kinetic evaluation of complex reactions. A good practice is to apply the moment based approaches for determining the type (reversible vs. irreversible) of interaction of feed components and reaction products and to use such knowledge for developing kinetic schemes for numerical calculations.63,108,111,123,124
On the basis of the order of appearance and shapes of transient responses, a detailed reaction scheme has been developed for oxidative propane dehydrogenation over VOx/TiO2 in the absence of gas-phase O2.123 It consisted of thirteen near to elementary reaction steps. Through validation of reaction parameters, only four elementary reactions were determined to be kinetically relevant. Propene formation is initiated by dissociation of the methyl C–H bond in propane on two lattice oxygen species, while propane activation through the methylene C–H bond on the same active sites results in surface precursors of CO2. Propene can also react with such species yielding adsorbed formate and acetaldehyde species, which are further oxidized to CO2. Unfortunately, the authors did not explain why the activation energy of methyl C–H bond dissociation is lower than that of methylene C–H bond activation. This result does not correspond to the dissociation energies of the corresponding C–H bonds, which are 410 and 395 kJ mol−1, respectively.
A comprehensive microkinetic model of NO reduction with H2 has been developed on the basis of kinetic evaluation of TAP experiments on Pt/Al2O3.114 The model includes several reaction pathways describing activation of H2 and NO, formation of H2O, N2, N2O and NH3 with participation of six surface intermediates (Table 3). It also explains the effect of temperature and H2 concentration on product selectivity. It is, however, worth mentioning that the TAP-derived kinetics were mainly aimed at elucidating possible reaction steps with the corresponding rate constants and activation energies as well as at explaining differences between the catalyst studies. There are only a few studies targeted at predicting steady-state operation at ambient or elevated pressures on the basis of the TAP kinetics derived from high-vacuum experiments. This is an important requirement if the kinetics should be used for optimizing reactor performance or predicting catalytic performance under conditions where experiments cannot be easily performed.
| Catalysts | Near to elementary reaction steps | Kinetic parameters | Ref. |
|---|---|---|---|
| N2O decomposition | |||
| FeOx/MFI | N2O + * → *–O + N2 N2O + *–O → O–*–O + N2 O–*–O → *–O2 *–O2 → O2 + * | Constants and activation energies of individual reaction steps | 108 |
| BaFeAl11O19 | N2O + * → *–O + N2 N2O + *–O → *–O2 + N2 N2O + *–O2 → *–O + N2 + O2 *–O2 ⇆ O2 + * | Constants and activation energies of individual reaction steps | 124 |
| RhOx/MFI | N2O + * ⇆ *–N2O *–N2O → *–O + N2 N2O + *–O → * + O2 + N2 O2 + * ⇆ *–O2 *–O2 + * ⇆ 2*–O | Constants and activation energies of individual reaction steps | 111 |
| NO reduction by H2 | |||
| Pt/Al2O3 | NO + Pt * ⇆ NO–Pt NO–Pt + Pt * ⇆ N–Pt + O–Pt 2N–Pt ⇆ N2 + 2Pt NO–Pt + N–Pt ⇆ N2O + 2Pt 2NO–Pt → N2O + O–Pt + Pt H2 + 2Pt ⇆ 2H–Pt H–Pt + O–Pt ⇆ OH–Pt + Pt OH–Pt + H–Pt → H2O + 2Pt NO–Pt + H–Pt ⇆ N–Pt + OH–Pt N–Pt + 3H–Pt ⇆ NH3–Pt + 3Pt NO–Pt + 3H–Pt ⇆ NH3–Pt + O–Pt + 2Pt NH3–Pt ⇆ NH3 + Pt NH3–Pt + 3-Pt → N–Pt + 3OH–Pt NH3–Pt + 3NO–Pt + 3Pt → 4N–Pt + 3OH–Pt | 114 | |
An attempt in this direction has been made for direct N2O decomposition over Rh–MFI, Fe–MFI and BaFeAl11O19.63,108,111,124 In addition, those studies provided kinetically relevant fundamentals for tailored catalyst design. Irrespective of the kind of FeOx species in MFI-type zeolites (Si/Al = 15 or ∞), the same microkinetic scheme was established to be valid for N2O decomposition (Table 3). However, the kinetics of oxygen formation was affected by this catalyst property. There is only one reaction pathway leading to O2, which is a complex sequence of three elementary reaction pathways (Table 3). This reaction is limited by the rearrangement of an adsorbed bi-atomic oxygen species to another one. The activation energy of this elementary step decreases with an increase in the degree of oligomerisation of FeOx species thus positively affecting catalyst activity for N2O decomposition. In addition to O2 formation, collision frequency of N2O with free MeOx (Me = Fe or Rh) sites or those with adsorbed oxygen species is also an important activity factor. It is higher for RhOx sites and polymerized FeOx species.
Another key factor determining de-N2O activity was concluded to be the mechanism of O2 formation. To check the potential of the obtained microkinetics for predicting steady-state activity, it was extrapolated from vacuum to conditions of standard catalytic tests (approximately over three orders of magnitude of N2O partial pressure).111,124 The microkinetic models qualitatively reproduced the activity order of differently composed catalysts in a wide range of temperatures and N2O partial pressures. Microkinetic models, on the basis of near-to elementary reaction steps, have been successfully derived from TAP experiments over a wide range of catalytic materials used in various complex heterogeneous reactions. The derived kinetic and mechanistic information was used to identify the origin of the catalyst activity and selectivity. It is, however, important to further validate the potential of TAP-derived microkinetics for the description of the steady-state catalyst performance.
3.3 Multi-pulse titration studies
As described in section 2.4.2, multi-pulse experiments introduce one reactant or a mixture of reactants as a long series of single pulses into the reactor. The aim is to induce a controlled change to the catalyst surface while at the same time monitoring a change in reactivity, referred to as a state-altering experiment, or to quantify the number of surface atoms by a “titration” type experiment. For example, a previously reduced surface can be transformed to a given oxidation state by introducing a series of oxygen or nitrous oxide pulses.63,64 Inversely, a fully oxidized surface can be reduced by using pulses of hydrogen, hydrocarbons or another reducing agent.60,99 Multi-pulse experiments (oxidizing and reducing) can also be conducted on fresh catalysts,125 as a way to assess the initial state of a catalyst. This process can be performed with great precision as the pulse intensity (i.e. number of molecules) is usually far less than the number of surface sites.38,71 Multi-pulse experiments allow studies of the effect of the degree of oxidation on the reaction rate and selectivity. Quantification of the data can be carried out at different levels. The number of surface atoms can be easily calculated from a “break-through” curve by integrating the zeroth moment for the complete series.31,71 Further data treatment allows extraction of specific kinetic parameters.71As an example, Fig. 6 reports the zeroth moment, M0, (equal to 1-conversion of O2) of a series of oxygen pulses over 1 wt% Pd/SiO2 at 100 °C.31 The first few pulses were completely adsorbed but then a break-through of oxygen was observed. The pulses were modelled by assuming a dissociative oxygen chemisorption. The model fit is also shown in Fig. 6. A value for the initial sticking coefficient of 0.24 was estimated from the data and the number of adsorption sites amounted to 30 × 10−5 mol gcat−1, corresponding to a dispersion of 32%. This multi-pulse experiment thus not only gave the number of adsorption sites and the sticking coefficient but also the dependence of the sticking coefficient on the surface coverage. The exponent α was estimated at 2.5, which is slightly higher than the value of 2 expected for dissociative oxygen chemisorption. In a similar way, it was also possible to estimate the metal dispersion and infer the size distribution of supported Rh NP in Rh/γ-Al2O3 catalysts possessing only 0.005 wt% of rhodium.63
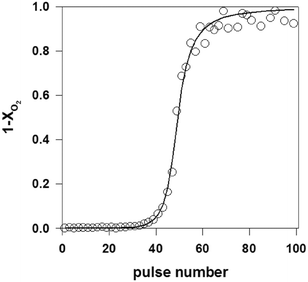 | ||
| Fig. 6 Oxygen breakthrough curve, i.e. fraction of oxygen released from TAP reactor after each subsequent pulse over a Pd/SiO2 catalyst (a series of 2 × 1015 O2 molecules per pulse are introduced over 10 mg of 1.0 wt% Pd/SiO2 catalyst at T = 100 °C). Open circles: experimental data, line: model.31 | ||
Multi-pulse experiments are a powerful tool to study reducible oxides as catalysts. The methodology and theory were developed and applied to different reactions.38,106 The TZTR configuration is especially suited for multi-pulse experiments as it leads to a homogeneous concentration of reactants and products across the catalyst bed. Another important step in the data analysis of multi-pulse experiments is to represent the data (conversion, yields or basic kinetic coefficients) as a function of the catalyst alteration state rather than as a function of the number of pulses. In this example, it will be accomplished by establishing an oxygen mass balance for each single pulse and thus calculating the degree of catalyst reduction or oxidation.106
In another example focused on the study of a water-gas shift catalyst, moment based methodologies have been used to extract the basic kinetic coefficients, while also identifying and quantifying the number of active sites of a 2% Pt/CeO2 catalyst.33,38 Different pre-treatment methods using O2, CO2, and H2O, to oxidize the Pt/CeO2 catalyst were employed. After the pre-treatment, the catalyst was reduced by a series of CO pulses. By plotting the CO conversion as a function of the total amount of CO consumed by the catalyst (i.e. the catalyst alteration state) the results showed that the three pre-treatments led to the same CO reactivity with the only difference being the initial number of oxidized sites, reflecting the reactivity of O2, H2O and CO2 towards the Pt/CeO2 catalyst (Fig. 7).38 The maximum changes in the catalyst state during these experiments occurred during the first few pulses when the CO conversion was the highest and amounted to less than 4 × 10−8 moles or ∼3% of the total amount of sites, emphasizing that the catalyst state is changed in a controlled manner. A total of more than 6000 pulses was necessary to fully reduce the catalyst.
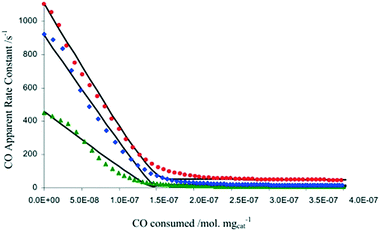 | ||
Fig. 7 CO apparent rate constant observed in CO multi-pulse experiments at 250 (green), 300 (blue), and 350![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) °C (red) over 3 mg of 2% Pt/CeO2 catalyst as a function of the CO consumed.38 °C (red) over 3 mg of 2% Pt/CeO2 catalyst as a function of the CO consumed.38 | ||
In summary, one of the advantages of multi-pulse experiments is that it is possible to alter the catalyst state/composition in a gradual/controlled manner. This allows characterization of the catalyst on a “state by state” approach by monitoring the amount of reactant consumed (and deriving apparent rate constants through moment based analysis) as a function of the surface composition or the number of pulses.65 The information obtained not only quantifies the number of active sites, but also the intrinsic activity of such sites, which is related to the gradient of the rate constant versus reactant consumed, as reported in Fig. 7.38 As such, it is possible to determine if there is one or more type of active site, for example in Fig. 7 there are two types of active sites which are determined from the two different gradients on each of the plots. This type of insight has been reported on a number of occasions.38,71
3.4 Studies with monoliths
While powdered catalysts have been the most commonly studied using TAP, the same methodologies have also been employed to characterize monolith catalysts for diffusivity60,126 as well as mechanistic and kinetic studies. For instance, the transient catalytic process of NOx storage and reduction on monolith washcoated with Pt/Al2O3 and Pt/Ba/Al2O3 have been studied (which were compared to analogous powdered catalysts) with the reactor configurations reported in Fig. 8.108,126,127 A range of multi-pulse and consecutive pulse (pump–probe) studies were applied in order to assess NO storage capacity,115,126 and mechanistic insight into the storage and reduction processes.108,126,127 Importantly, similar results were reported for the powdered catalysts and the monoliths.126 NO pulse experiments revealed a mechanism that combined both NO decomposition and storage.126 This mechanism infers a spillover of oxygen adatoms from the Pt to the Ba phase, producing BaO2 which is then involved in NO storage via barium nitrate.126,127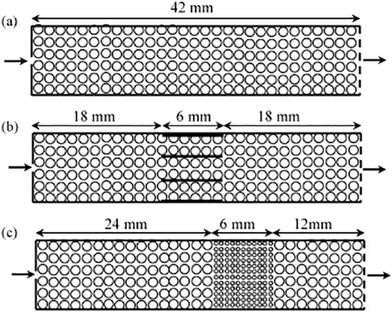 | ||
| Fig. 8 Schematics of one-zone inert (a), three-zone monolith (b), and three-zone powder (c) configurations.127 | ||
The role of Pt in the catalyst for NOx storage was also summarized:126,127
• Catalysing the oxidation of NO to NO2 which stores on BaO by spill over mechanism.
• Decomposition of NO2 to NO.
• The Pt/Ba ‘couple’ is an integral element for adspecies spill over to BaO.
The results from these studies suggest that the major mechanism for NOx storage is the NOx spillover at the Pt/BaO interface, which was confirmed by 14NO–15NO isotopic exchange experiments.118 As would be expected, a higher N2 release is observed for Pt/Ba/Al2O3 compared to Pt/Al2O3 which suggested a higher storage on the catalyst with Ba.127 The scavenging role of H2 freeing up of the sites for decomposition and reduction of stored NOx was also identified.126 This type of work reinforces that TAP is versatile in terms of types of sample which can be studied, and that the same operating modes can be applied irrespective of the type of sample.
3.5 Single particle experiments
A recent novel example using the catalytic oxidation of CO over a single Pt particle demonstrates the unique information that can be obtained from TAP experiments by cycling between different experimental regimes.18 This is seen as a route to bridging the ‘material gap’ since transport data (diffusion) and intrinsic kinetic data (e.g. number of active sites, site activation energy, etc.) obtained from TAP transient response experiments on single crystals can be correlated with experiments performed on multi-crystalline materials.128
Fig. 9 illustrates key elements of a single particle Knudsen pulse response experiment. The microreactor is packed with approximately 100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 inert quartz particles (210–250 μm in diameter) and a single Pt particle with an equivalent spherical diameter of 300–350 μm. The particle is positioned in the centre of the packed bed and the internal temperature adjacent to the particle is sampled with a shielded thermocouple. The Pt particle fills <0.3% of the reactor cross-section and occupies <.003% of the reactor volume. The Pt particle has a complex micro-structured surface but the bulk solid is nonporous. Likewise, the inert quartz particles are nonporous so that gas diffusion or mass transfer within particles does not occur. A series of O2/Ar (70/30 feed ratio) pulses, each containing approximately 1014 oxygen molecules were pulsed into the microreactor. Conversion was 100% for the first pulse and greater than 90% for the second pulse. After approximately 40 pulses the O2 conversion dropped to zero.
000 inert quartz particles (210–250 μm in diameter) and a single Pt particle with an equivalent spherical diameter of 300–350 μm. The particle is positioned in the centre of the packed bed and the internal temperature adjacent to the particle is sampled with a shielded thermocouple. The Pt particle fills <0.3% of the reactor cross-section and occupies <.003% of the reactor volume. The Pt particle has a complex micro-structured surface but the bulk solid is nonporous. Likewise, the inert quartz particles are nonporous so that gas diffusion or mass transfer within particles does not occur. A series of O2/Ar (70/30 feed ratio) pulses, each containing approximately 1014 oxygen molecules were pulsed into the microreactor. Conversion was 100% for the first pulse and greater than 90% for the second pulse. After approximately 40 pulses the O2 conversion dropped to zero.
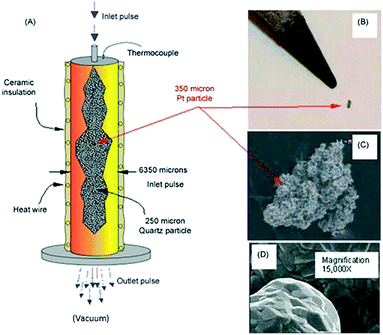 | ||
Fig. 9 A) Schematic of TAP microreactor single particle configuration. (B) Actual image of single particle Pt polycrystalline catalyst taken with a digital camera. (C) SEM images showing the entire polycrystalline Pt particle. (D) Inset gives high magnification (15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000×) SEM image of Pt particle surface.18 000×) SEM image of Pt particle surface.18 | ||
Single particle CO oxidation experiments were also performed using the pump–probe format and the same packed bed and Pt particle.18 Mixtures of O2/Ar (70/30) and CO/Ar (70/30) stored in separate pulse valves were injected into the microreactor forming a train of alternating pulses of O2 and CO. At 140 °C the CO2 response on the O2 pulse is significantly broader than the CO2 response on the CO pulse. The broader response indicates that CO2 is evolved more slowly on the O2 pulse then on the CO pulse. The difference in responses provides clear evidence that the surface reaction mechanisms are not equivalent. At 350 °C the CO2 response on the O2 pulse is almost non-existent, while the CO2 response on the CO pulse appears very similar to the response at 140 °C. These results indicate that the CO surface lifetime is shorter than the CO–O2 pulse interval and that the oxygen surface lifetime is longer than the O2–CO interval.
In Fig. 10, the normalized M0 of the different CO2 responses collected at different temperatures is plotted versus temperature. The red and blue plots show the CO2 yield for the individual O2 and CO pulses, respectively. The black plot represents the total CO2 yield obtained by summing the individual yields during one pump–probe cycle. At 170 °C the CO2 yield is greater than 95% indicating that more than 95% of the CO and O2 molecules collide with the Pt particle and react. Above 170 °C the CO2 yield decreases more rapidly for the O2 pulse than the CO pulse. From 170 to 350 °C, the CO2 yield on the oxygen pulse decreases from a maximum of 52% to <5%. In the same interval, the yield on the CO pulse decreases from 43% to 25%, so that the overall yield drops from 95% to less than 30%. During the O2 pulse, oxygen reacts with CO molecules adsorbed during the CO pulse. During the CO pulse, the reverse is true with CO molecules reacting with different forms of adsorbed oxygen. In the latter case, the CO2 yield decreases more slowly indicating that the oxygen surface lifetime is longer. The yield peak (turning point) for all three curves occurs at the same temperature of 170 °C. The yield peak represents the point of maximum surface coverage for both CO and O2.
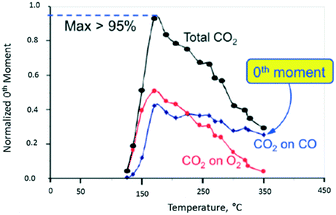 | ||
| Fig. 10 CO2 production observed from vacuum pump–probe experiment over a single Pt particle. The black line represents the total CO2 yield. The red and blue lines represent the CO2 yield on the oxygen pulse and CO pulse, respectively.18 | ||
After completing the set of vacuum pulse response experiments, the slide valve was closed so that the reactor could be operated at atmospheric pressure. The temperature dependence of the CO2 yield was characterized by two branches, which formed a counter-clockwise hysteresis loop. For the flow experiments, the lower branch of the hysteresis loop occurred during the up ramp and the upper branch during the down ramp (Fig. 11). On the lower branch of the hysteresis loop, around 350 °C, a rapid rise in CO2 yield was observed.
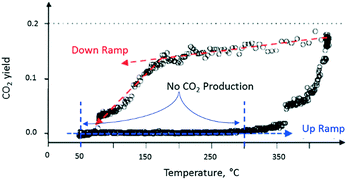 | ||
| Fig. 11 CO2 production observed from atmospheric flow experiment over a single Pt particle. The CO2 produced while increasing reactor temperature is less than the CO2 produced during reactor temperature decrease as shown by the counter-clockwise hysteresis loop.18 | ||
On the upper branch of the hysteresis loop (Fig. 11), a maximum in CO2 production of 20% was observed at 430 °C. At 170 °C (turning point), the slope of the temperature changes and a significant decrease of CO2 occurred. The turning point occurred at the same temperature as that observed in the pump–probe experiments. The phenomenon, denoted yield hysteresis, is well known in heterogeneous catalysis, and has been previously observed in CO oxidation reaction over noble metals. The hysteresis is due to changing surface coverage and not local heating. While flow conditions offer limited control of surface coverage, TAP pulsing enables pulse-by-pulse control. In these experiments the effects of surface coverage on reaction kinetics were observed in both regimes, bridging the pressure gap. The behaviour is attributed to competition between O2 and CO for active catalytic sites on the metal surface. The turning point can be viewed as the temperature at which O2 domination on the Pt surface switches to CO domination.
In summary, conversion during atmospheric pressure experiments was quite high. The residence time in the microreactor was longer than in a TAP experiment, but the apparent contact residence time in the reaction zone is about 2 orders of magnitude less. Nevertheless, CO conversion reached 20%. Clearly, the real residence time in the reaction zone was larger, and mixing was also significant in atmospheric flow experiments. The calculated reaction constants for the two different reaction regimes were within 3%. The correspondence in turning points indicates that the coverage in vacuum and atmospheric pressure experiments was approximately the same and intrinsic kinetic data obtained in vacuum experiments could be used to describe kinetic behaviour in the atmospheric pressure domain. The ‘single particle experiment’ showed the remarkable sensitivity of the TAP reactor system when performing kinetic experiments at both vacuum and elevated pressures.18
4 Evolution of TAP
4.1 Detectors
The main features of TAP-1, TAP-2 and TAP-3 are discussed in detail elsewhere.5,7,8,14 Some customized systems similar to TAP129–131 have also been reported as well as variations on the original concept designed for specific purposes, such as the multiple time resolved analysis of catalytic kinetics (MULTITRACK)8,132 and the paralleled TAP system.133 In this section, the latest development in terms of TAP technology development are reported.To date, quadrupole mass spectrometers (QMS) have been used almost exclusively to monitor TAP experiments as they provide a good time resolution, are versatile and have a sufficiently wide dynamic range to provide high sensitivity. In order to provide the desired time resolution, a typical QMS is limited to observing only one AMU per pulse cycle during a TAP experiment. This raises issues in terms of experiment duration, and indeed in terms of data integrity with regards to possible “unobserved” changes in pulse response, which is dependent on the total number of AMUs being monitored. Time of flight mass spectrometers (ToF MS) offer the opportunity to observe all masses simultaneously. In this type of MS, all ions which have identical kinetic energy are injected in a flight tube where they separated according to their respective masses.61 This is achieved by the ions with smaller masses arriving at the detector faster than ions with larger masses i.e. ions with smaller mass will have a shorter “flight time”.134
The ToF characteristics offer multiple opportunities and advantages for TAP applications. First, the density of data is much higher than in the case of the QMS, since all masses are recorded for each pulse. The second, which is historically linked to the TAP development, is the possibility to detect “unexpected” reaction intermediates. In ToF, the whole mass spectrum can be recorded with a sub-millisecond time resolution, which offers the possibility of wide-net “chasing” of evolution of masses. Conversely, the QMS requires the pre-selection of a mass to be analysed, which make the identification of unexpected intermediates more tedious. This point is not unique to TAP since some steady state methods utilizing MS would also need a pre-selection of the masses in order to access suitable time resolution and reduce computer processing time delays.
In order to observe multiple masses simultaneously, a ToF MS for TAP was developed.135 While this ToF MS did provide millisecond time resolution, it was not adequate in terms of the sensitivity required for the TAP technique.8 More recently, another ToF MS was custom built for TAP applications.136 It was demonstrated that this TAP ToF MS has the detector linearity, reproducibility and high sensitivity that is essential to accurately analyse TAP pulse response experiments.136 The development of this instrument has provided a technology which can be more widely applied to other techniques, including fast transients, which require high time resolution for analysis or require the ability to screen for previously undetected intermediates. This has been acknowledged in a review on high resolution mass spectrometry for the wider analytical chemistry audience.137
4.2 Analysis
TAP pulse experiments can provide quantitative information such as rate constants of elementary steps and the number of active sites present. In order to obtain these type of information it is necessary to process the experimental results with the appropriate data analysis tools. The analysis approach is influenced by the types of configuration for the TAP microreactor packing selected. There are three main configurations: the original one-zone configuration (microreactor is completely filled by catalyst), the three-zone configuration (catalyst layer is sandwiched between two layers of inert material) and the thin-zone configuration (the catalyst layer is significantly smaller than the inert layers). Each of these are described extensively in the literature previously.14,34,36,61,63,65,106,118,138There are a number of approaches/methodologies in the TAP data analysis which are discussed in detail in the literature, including the moment-based integral approach,19,106,140,141 differential approach,142 curve fitting,31,108,123,124,127,143–149 as well as the extraction of kinetic parameters.19,106 Briefly, the moment-based theory106 is an integral analysis of each individual pulse in the series of pulses, both reactants and products. From the first three moments (time-weighted area under the pulse response; M0, M1 and M2) three primary/basic kinetic coefficients (r0, r1, r2) can be calculated.33 These experimentally derived basic kinetic coefficients each present unique physico-chemical meaning.106 Materials can be compared on the basis of the primary kinetic coefficients without assumption of a model or data can be interpreted in terms of various models with rate constants of various reaction mechanisms described in an extensive reference table available in the literature.106 The expressions depend on the reactor configuration, but rather simple expressions arise in the case of a TZTR.33
Curve fitting is another commonly used approach where the experimental transient responses are fitted to different assumed kinetic models.31,143–149 The most plausible model is selected on the basis of model discrimination tests. The parameter (rate and diffusion coefficients, as well as activation energy) estimation procedure is based on a numerical solution of partial differential equations describing diffusion, adsorption, desorption, and reaction in the TAP microreactor. To this end, non-commercial software packages developed in different research groups are applied.31,148,149 Analytical advances specific to the TAP methodology have also been reported.146,150–154
Since 2001 a step-by-step advancement of the mathematical theory of the TAP “reaction–diffusion” systems has been constructed, including:
• The theory of multi-zone TAP-reactors.155–159
• The probabilistic theory160,161 for determining how the local geometric structure of a channel surface influences the diffusivity properties of an inert gas in the Knudsen regime. This geometry, referred to as the channel microgeometry, is encoded in the scattering operator, P. The theory can be extended to the “diffusion–reaction” systems for revealing the local microgeometry of the active centre.
• The special model-free procedure (the so called Y-procedure) to extract the reaction rate inside the catalytic reactor at any moment of time based on the measured exit flow.162,163 It is believed that the Y-procedure will be a basis of advanced software for non-steady-state kinetic data interpretation. Practical applications of the Y-procedure already exist.164
• The theory of elucidating catalytic mechanisms.165 Within this theory, the new fingerprints and “decision tree” procedure were described for discriminating mechanisms of complex reactions.
Most aspects of data analysis are extensively covered elsewhere in the literature,18,19,31,108,123,124,127,140–149,155–165 including in review papers,5,7,8 and are not discussed in detail in the present work. In the following sections, a number of recent advances which can have application and impact beyond the field of TAP are discussed in more detail.
In essence, the adsorptive nature of reactants and products can be assessed over a one-zone configuration of the inert material. This is done via the direct comparison of the experimental curve with the purely diffusional response of the species, based on pure Knudsen diffusion.166 Consequently, any additional delay (i.e. due to adsorption/desorption) can be quantified and as such can be subtracted from the processes observed later on when using a typical TZTR configuration, thereby ensuring the reported insights are those related solely to the catalyst. This analytical method was validated using the selective reduction of oxygen in a hydrogen rich ethylene feed over silver catalysts, and provides a basis to ensure greater confidence in TAP data analysis, even when facing adsorption in the inert zone of the microreactor packing.166
While this addressed an issue arising from a TAP experiment, it highlights a sometimes overlooked wider issue. Any experiment which uses an inert material, for example to improve thermal conductivity/preheating of gas, assumes that there is no interaction between the reactant gases and this inert material, yet it is apparent that this is not always the case.166
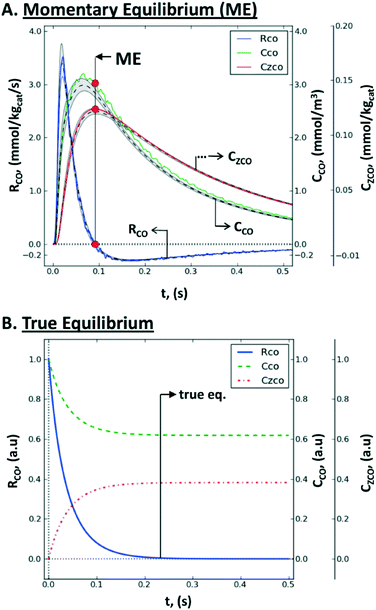 | ||
| Fig. 12 Non steady-state consumption rate, RCO(t), gas concentration, CCO(t), and surface concentration, CZCO(t), of CO during a single-site reversible adsorption: (A) rate-concentration data during a TZ TAP pulse-response experiment: simulated values within the catalyst zone (gray-shaded area), mean simulated values (dashed line), values reconstructed by the Y-procedure (solid line), momentary equilibrium (red circles), and the uncertainty range (between vertical dotted lines); (B) rate-concentration data during a batch experiment in a closed system, i.e., the approach of true chemical equilibrium.167 | ||
Consequently, the whole consumption rate of the single component is zero. Knowing the gas concentration and the uptake of the substance at the ME point, one can determine the number of active sites per unit of the catalyst surface. In terms of application, a pulse-intensity modulation method based on chemisorption was reported for the characterization of CO adsorption on a hydrotalcite-supported platinum catalyst (1% wt Pt/Mg(Al)O).167
This approach addresses the difficulty in quantifying the true number of active sites in catalytic reaction. Traditionally, this is done using probe molecule chemisorption. However, it should be noted that the number of active sites based on chemisorption measurements may significantly differ from the number of reactive sites.168,169
To address this issue, the SSITKA method, proposed by Happel170,171 and developed by Bennett172 and Biloen,173 provides an elegant technique174 which allows the determination of the surface concentration of the most active reaction intermediates (mari) under reaction conditions. According to the idea of the SSITKA approach, after a step-change between two reactant streams containing different isotopes, distributions of isotopically labelled products are monitored using a MS. SSITKA studies are used to determine the amount of substance stored/released by a surface. However, by definition, the SSITKA method provides information about the number of active sites under steady-state reaction conditions. In the literature there has been a report of good correlation between quantification of active sites by TAP38 and by SSITKA.43 This has shown the potential of TAP experiments to provide relevant analysis regarding the active sites of a catalyst and mechanisms of catalytic processes.
The advantage of the momentary equilibrium TAP method (METAP) is that it interrogates the catalyst under conditions close to reaction conditions but does not need expensive isotopically labelled compounds. As such, this method can be used to bridge the “pressure gap” through the quantification of the catalytic sites by TAP-derived kinetics to those obtained by other techniques. It has been stated that ME has the potential to be applicable for processes where reversibly adsorbed species are required to be present under equilibrium, at predefined spatial and temporal positions.167
The method entails the plotting of the response in the logarithmic scale, thereby translating the “tail” of the response to a straight line, the equation of which is then determined. By utilizing the exponential of the equation of this straight line, it is possible to generate the remainder of the pulse response, thereby allowing for further TAP data analysis via the established methods (see section 4.2), an example of which is reported in Fig. 13.
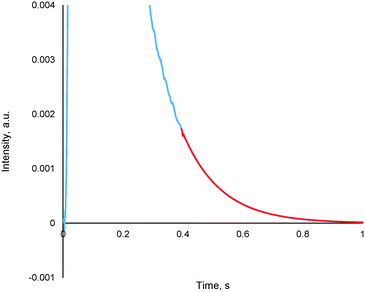 | ||
| Fig. 13 A truncated argon pulse response (blue) which has had its remainder generated through tail expansion (red). | ||
This methodology was extensively validated for inert, reactant and desorbing product in recent literature.175 An example of some results are reported in Fig. 14, where an argon pulse response has been experimentally collected correctly and was then artificially truncated. The truncated response was then processed using the expansion method detailed within this section as well as by two other methodologies which are commonly used previously (forced baseline and terminal baseline), even though these methods are known to underestimate the moments.175 As can be seen from Fig. 14, the expansion method could determine the moments more accurately than either the forced baseline or terminal baseline approaches. This methodology would be useful in situations which are both time and material sensitive, i.e. it may be quicker and less expensive to conduct this type of mathematical expansion as opposed to repeating the experiments again. Similar methodologies which report an exponential like decay response and encounter data acquisition/human error issues could also adapt the reported approach to overcome incomplete data sets.
5 Revitalizing the TAP technique
Despite the fact that TAP can provide important insights and understandings of catalytic processes, it has not been widely adopted by the catalysis community. Undoubtedly some of the reasons for this resides with the small number of instruments currently in use, the perceived complexity of the instrument and the special skills set required for transient data analysis. Within this section, the potential for TAP to be applied in conjunction with modern and emerging catalyst assessment methodologies is proposed.5.1 TAP relevance in current catalyst research
Driven by stringent environmental legislation and limited natural reserves,9,10 the development of more efficient and/or alternative catalytic routes has become a priority for modern and future industry. Since catalysts are key enablers for meeting such challenges, the development of new materials with desired properties is one the main targets of the ongoing research. To this end, a fuller understanding of catalysts and catalytic processes is required. Particularly when using complex reactant mixtures it is critical that an in-depth understanding of the mechanisms and kinetics of surface reactions is obtained.6 As such, experimental measurements, on as elementary a level as possible, are key to this understanding. While traditional catalyst methods such as CSTR and PFR are still used extensively there has been an emerging trend of developing new methods such as stagnation flow reactors,176 as well as developing operando modes for existing catalyst characterization, some of which are incorporating spatial and temporal measurements of reaction distributions of concentration and temperature for structured catalyts6,177–179 and for powdered catalysts.180–182Despite the proven potential of operando techniques for identifying catalytically active species/centres/phases and for elucidating reaction mechanisms, they typically fail to provide a molecular picture of catalytic reactions including microkinetics because of low time resolution, i.e. in many processes there are short lived intermediates which may not be detected due to incompatible time resolutions. Moreover, it is very difficult to ensure isothermal conditions when investigating highly endo or exothermic reactions thus significantly complicating kinetic and mechanistic studies. Since the TAP technique is free of the above limitations as demonstrated by several studies over powders and a range of other catalytic materials (including monoliths,57,126,127 single particles18 and wires40) as discussed in the current work, clearly there is the potential for results from TAP experiments to become very useful to these current advances in catalytic assessment. The use of metal organic frameworks (MOFs) for heats of adsorption studies has also been reported.183
In order for some of this potential to be realized it is evident that some development of TAP experimental methodology/instrumentation as well as analysis/models is required (see section 5.2). With this in mind, the authors' have a number of goals with a view to ensure further and continued application of TAP in modern catalytic investigations.
5.2 Ambitions for future development of TAP
Some processes are difficult to study using TAP, such as isomerization, although it may still be possible to study these using some previously suggested solutions, such as independent determination of reactant product composition of the reaction products.5 Given the current trends in catalytic investigation, it is desirable to now start investigating more complex reactions than those previously reported5,7,8 and discussed herein, with the focus on identifying near-to elementary reaction pathways and to determine their kinetic parameters. While the analytical methods themselves are free of limitations with respect to the complexity of kinetics models, there is still a drawback with computing power, which is, fortunately, continuously improving.184 With increased complexity of reaction studied, there will also be the need to further develop the current analytical and numerical methods. To avoid over parameterization of microkinetic models used for the latter approach, it is highly important to use model-free analysis for identifying reaction pathways.162,163 To this end, the moment based approaches for determining the type of interaction (reversible vs. irreversible) of feed components and reaction products should be taken into account. However, it has previously been limited to relatively simple processes, and is not ideal for extraction of kinetic parameters for products. Consequently, the application of moment based analysis would need to be expanded, something which is currently ongoing.185One of the other limitations is linked to the use of QMS and, to a lesser extent, even the recent TAP ToF approaches.135,136 While complex reactions can already be studied, the MS methods used, so far, are limited to a resolution of 1 atomic mass unit (AMU) and multiple species can contribute to the same apparent masses; for example N2 and CO both have a mass of 28. In order to discriminate between these species, it is necessary to use fragment masses and full mass deconvolution which is tedious for simple cases and sometimes impossible for more complex cases. It is also worth noting that these manipulations are detrimental to the signal to noise ratio. The issue of different species sharing the same apparent mass, however, can be overcome. In the case of CO and N2, these two species actually have different masses (N2: 28.014 and CO: 28.010). A mass spectrometer with sufficient mass resolution would be able to discriminate these two masses, and with advances in technology equipment with such capability and appropriate time resolution should now be possible,186 and as such is a primary ambition in terms of development of TAP instrumentation.
With the emergence of operando catalyst characterization techniques providing information on the catalyst under true working conditions, the ability of TAP to provide results that are industrially relevant is even more significant. We have already discussed the advantage of the high time resolution of TAP to provide industrially relevant information, by being able to distinguish between separate processes (section 3). There is a long history of direct industrial involvement in research with TAP, including, but not limited to, BASF,187 Dupont,136,188–191 Haldor Topsøe,192 Johnson Matthey,193–196 Monsanto,14,197–199 Shell18,188,200,201 and Toyota.78,202,203 There is also evidence of topical TAP research which is relevant to industrial applications such as the Toyota Di-Air system,204,205 reactions of methane,206,207 NOx catalysis110,203,208,209 and for better understanding of catalysts used in the production of industrial chemistry building blocks.49,124 There is still industrial involvement in TAP research, though most recently this has been sponsorship of projects, either financially and/or through the supply of materials and for confidentiality purposes, such studies are not always reported in the literature.
To build further on this tradition of industrial collaboration, a framework should be devised in order to provide added vigour/robustness to TAP results in order to improve their applicability. One way in which this can be done is to check/quantify the effect of any pressure gap through the evaluation of small and large pulse intensity experiments, thereby varying the total pressure during those pulse response experiments. Until such experiments are conducted and reported it will not be possible to validate the use of existing analytical methods, or indeed any newly developed analytical methods formulated for the proposed operating conditions. It would also be possible to examine the role of gas phase reactions, since these are eliminated in the Knudsen diffusion regime, through direct comparisons of experiments with and without these gas–gas interactions.
With the significant developments in operando spectroscopy it is possible to characterize metal oxidation state and to correlate structures with observed catalytic behaviour. Given that catalysts often adapt to their environment, i.e. undergo a change in metal oxidation state/structure/coordination, operando techniques have the ability to detect such changes and determine catalytically active structures,6 although it may not be possible to derive accurate kinetics of elementary steps due to temperatures distribution. Spatially resolved operando techniques further provide the ability to obtain spatial resolution of such correlations between structure and catalyst performance.6 Given that TAP is one of the only techniques that allows control of state and targeted kinetics characterization of catalyst through state defining approach,210 information from operando methods could be used to design TAP experiments which can provide accurate kinetics of elementary steps. Similarly, data from TAP experiments which would indicate a specific catalytically active state could be used to help design appropriate operando experiments in order to gain further understanding. As an example, if TAP detected that a reduced catalyst was more active for a process than an oxidized catalyst (or vice versa), this could shape operando experiments in terms of the conditions used and, indeed, even in terms of the spectroscopy that should be used in operando mode for such experiments.211
Computational catalysis such as density functional theory (DFT) has become an essential part of the discipline during the past decade. A further benefit of the utilization of operando spatially resolved techniques has been the ability to utilize experimentally derived data to improve numerical analysis/predictions, including microkinetic models.6,182 While TAP has readily contributed to the bridging of the material and pressure gaps, there is now the potential for TAP to assist with the knowledge gap6,212 that exists between experiment and kinetic modelling. An important issue, which is rarely tackled in transient kinetic analysis, is the relevance of unsteady-state kinetics for predicting steady-state catalyst performance. TAP experiments should be used to provide direction in terms of mechanism and by providing experimental kinetic data and diffusion coefficients that can be used as a foundation for modelling. There is evidence that this is already occurring,213 while there are also reports of comparisons of kinetics derived from TAP and DFT.52 The justification for the use of parameter inputs from TAP can be critically assessed for relevance by the ability of the models to predict the experimentally observed results, which is a typical test required for model validation in any case.
The use of all methods at our disposal (modelling, operando experiments and transient experiments) in the complimentary ways outlined herein can only serve to improve upon our understanding of catalytic processes, and therefore address the aforementioned global challenges. Furthermore, and perhaps most critically, in order to facilitate wider adoption of the TAP as a complimentary methodology, it is now necessary to create a user-friendly software that will unify all the data reduction and analysis methods published so far and will be freely available to the catalysis research community. The present authors have already started this initiative, with a view to not only provide the necessary analytical capability, but also to aid proper application of the experimental methods in order to provide the most beneficial information.
6 Conclusions
The significant contributions and the value of the TAP methodology to furthering the understanding of catalysts and catalytic processes have been discussed above. The community which utilizes the technique still remains relatively small nearly forty years later, which means that TAP is very much a niche methodology. There are, however, significant literature contributions, of which the references of the current work are not an exhausted list, and it is clear that the desire to utilize the TAP methodology is strong. To summarize, the key advantages of TAP, as highlighted herein and in the literature,5,7,8 are:• Small volume of gas per pulse: effective use of expensive isotopes.
• Millisecond regime.
• Operation in Knudsen diffusion regime: no mass transfer limitations.
• Isothermal catalyst zone.
• No material gap: model and practical catalysts can be used.
• Bridging of pressure gap: range of pressures from UHV to high pressure are accessible.
• The ability to conduct state defining experiments.
• The ability to conduct state altering experiments.
• Extraction of kinetic parameters.
• The ability to decipher reaction mechanisms.
The relevance of the technique to current trends in catalyst characterization has also been discussed, and indeed a number of scenarios have been proposed as to how TAP can evolve and continue to contribute to modern catalytic assessments. It has been the aim of the current work to address some of the mystique of TAP so as to give the methodology wider appeal and to make it more accessible. TAP is certainly unique in its capabilities to extract mechanistic insights and kinetic parameters, and with some further development, it is the authors' hope and determination that this catalytic kinetic analysis methodology will become much more prominent.
U.S. Department of Energy disclaimer
This information was prepared as an account of work sponsored by an agency of the U.S. Government. Neither the U.S. Government nor any agency thereof, nor any of their employees, makes any warranty, express or implied, or assumes any legal liability or responsibility for the accuracy, completeness, or usefulness of any information, apparatus, product, or process disclosed, or represents that is use would not infringe privately owned rights. References herein to any specific commercial product, process, or service by trade name, trademark, manufacturer, or otherwise, does not necessarily constitute or imply its endorsement, recommendation, or favouring by the U.S. Government or any agency thereof. The views and opinions of authors expressed herein do not necessarily state or reflect those of the U.S. Government or any agency thereof.Notes
Fig. 6 is reprinted from ref. 31, Copyright (2007), with permission from Elsevier. Fig. 7 is reprinted from ref. 38, Copyright (2008), with permission from Elsevier. Fig. 8 is reprinted from ref. 127, Copyright (2009), with permission from Elsevier. Fig. 9–11 are reprinted from ref. 18, Copyright (2008), with permission from Elsevier. Fig. 12 is reprinted from ref. 167, Copyright (2013) American Chemical Society.Acknowledgements
Queen's University Belfast wish to thank EPSRC UK for funding under the CASTech (EP/G02152X/1) project. Funding of studentships by Department of Employment and Learning NI are also acknowledged. KM, RF, GY and JTG would like to acknowledge J. M. Yoda for many fruitful discussions. RF would like to acknowledge this work was supported by the U.S. Department of Energy, under DOE Idaho Operations Office Contract DE-AC07-05ID14517. Accordingly, the U.S. Government retains a nonexclusive, royalty-free license to publish or reproduce the published form of this contribution, or allow others to do so, for U.S. Government purposes.References
- J. Hagen, Shape-Selective Catalysis: Zeolites in Industrial Catalysis: A Practical Approach, Wiley-VCH Verlag GmbH & Co. KGaA, Weinheim, Germany, 2006, pp. 239–259 Search PubMed.
- S. B. Rasmussen, M. A. Bañares, P. Bazin, J. Due-Hansen, P. Ávila and M. Daturi, Phys. Chem. Chem. Phys., 2012, 14, 2171 RSC.
- G. Rothenberg, Heterogeneous Catalysis in Catalysis: Concepts and Green Applications, Wiley-VCH Verlag GmbH & Co. KGaA, Weinheim, Germany, 2008, pp. 127–187 Search PubMed.
- I. Chorkendorff and J. W. Niemantsverdriet, Introduction to Catalysis in Concepts of Modern Catalysis and Kinetics, Wiley-VCH Verlag GmbH & Co. KGaA, Weinheim, Germany, 2003, pp. 1–21 Search PubMed.
- J. T. Gleaves, G. Yablonsky, X. Zheng, R. Fushimi and P. L. Mills, J. Mol. Catal. A: Chem., 2010, 315, 108 CrossRef CAS.
- K. Morgan, J. Touitou, J.-S. Choi, C. Coney, C. Hardacre, J. A. Pihl, C. Stere, M.-Y. Kim, C. Stewart, A. Goguet and W. P. Partridge, ACS Catal., 2016, 6, 1356 CrossRef CAS.
- J. T. Gleaves, G. S. Yablonskii, P. Phanawadee and Y. Schuurman, Appl. Catal., A, 1997, 160, 55 CrossRef CAS.
- J. Pérez-Ramírez and E. V. Kondratenko, Catal. Today, 2007, 121, 160 CrossRef.
- C. Hageluken, Platinum Met. Rev., 2012, 56, 29 CrossRef.
- K. Morgan, A. Goguet and C. Hardacre, ACS Catal., 2015, 5, 3430 CrossRef CAS.
- H. Tanaka, M. Taniguchi, N. Kajita, M. Uenishi, I. Tan, N. Sato, K. Narita and M. Kimura, Top. Catal., 2004, 30/31, 389 CrossRef CAS.
- B. Jandeleit, H. W. Turner, T. Uno, J. A. M. van Beek and W. H. Weinberg, CATTECH, 1998, 2, 101 CAS.
- S. Senkan, Angew. Chem., Int. Ed., 2001, 40, 312 CrossRef CAS PubMed.
- J. T. Gleaves, J. R. Ebner and T. C. Kuechler, Catal. Rev.: Sci. Eng., 1988, 30, 49 CAS.
- M. Olea, M. Tada, Y. Iwasawa, V. Balcaen, I. Sack, G. B. Marin, D. Poelman and H. Poelman, J. Chem. Eng. Jpn., 2009, 42, s219–s225 CrossRef.
- G. S. Yablonsky, M. Olea and G. B. Marin, J. Catal., 2003, 216, 120 CrossRef CAS.
- O. Hinrichsen, A. C. van Veen, H. W. Zanthoff and M. Muhler, TAP Reactor Studies in In Situ Spectroscopy in Heterogeneous Catalysis, ed. J. F. Haw, Wiley-VCH Verlag GmbH & Co. KGaA, Weinheim, Germany, 2002, pp. 237–269 Search PubMed.
- X. Zheng, J. T. Gleaves, G. Yablonsky, T. Brownscombe, A. Gaffney, M. Clark and S. Han, Appl. Catal., A, 2008, 341, 86 CrossRef CAS.
- G. B. Marin and G. Yablonsky, Temporal Analysis of Products: Principles, Applications and Theory in Kinetics of Complex Reactions. Decoding Complexity, Verlag GmbH & Co. KGaA, Weinheim, Germany, 2011, pp. 319–382 Search PubMed.
- http://www.nobelprize.org/nobel_prizes/chemistry/laureates/1986/ (accessed 6/23/ 2016).
- http://www.nobelprize.org/nobel_prizes/chemistry/laureates/1967/ (accessed 6/23/ 2016).
- C. O. Bennett, AIChE J., 1967, 13, 890 CrossRef CAS.
- C. O. Bennett, Experiments and processes in the transient regime for heterogeneous catalysis in Advances in Catalysis, ed. W. O. Haag, B. Gates and H. Knözinger, Academic Press, San Diego, USA, 2000, pp. 329–416 Search PubMed.
- J. A. Schwarz and R. J. Madix, Surf. Sci., 1974, 46, 317 CrossRef CAS.
- R. P. Merril and R. J. Madix, J. Vac. Sci. Technol., 1977, 14, 1282 CrossRef.
- D. M. Golden, G. N. Spokes and S. W. Benson, Angew. Chem., Int. Ed. Engl., 1973, 12, 534 CrossRef.
- J. T. Gleaves, Research Proposal, 1977 Search PubMed.
- A. M. Efstathiou, J. T. Gleaves and G. S. Yablonsky, Transient Techniques: Temporal Analysis of Products and Steady State Isotopic Transient Kinetic Analysis in Characterization of Solid Materials and Heterogeneous Catalysts: From Structure to Surface Reactivity, ed. M. Che and J. C. Védrine, Wiley-VCH Verlag GmbH & Co. KGaA, Weinheim, Germany, 2012vol. 1 & 2, pp. 1013–1073 Search PubMed.
- M. P. D’Evelyn and R. J. Madix, Surf. Sci. Rep., 1984, 3, 413 CrossRef.
- J. T. Gleaves, Preliminary TAP results, 1979 Search PubMed.
- Y. Schuurman, Catal. Today, 2007, 121, 187 CrossRef CAS.
- M. Knudsen, Ann. Phys., 1909, 333, 75 CrossRef.
- S. O. Shekhtman, N. Maguire, A. Goguet, R. Burch and C. Hardacre, Catal. Today, 2007, 121, 255 CrossRef CAS.
- S. O. Shekhtman, Interrogative kinetics: A new methodology for catalyst characterization, PhD dissertation, Washington University in St. Louis, 2003 Search PubMed.
- J. W. Niemantsverdriet, A. F. P. Engelen, A. M. de Jong, W. Wieldraaijer and G. J. Kramer, Appl. Surf. Sci., 1999, 144–145, 366 CrossRef CAS.
- N. Maguire, Transient Kinetics, PhD Thesis, Queen’s University Belfast, 2010 Search PubMed.
- A. Goguet, S. O. Shekhtman, R. Burch, C. Hardacre, F. C. Meunier and G. Yablonsky, J. Catal., 2006, 237, 102 CrossRef CAS.
- S. O. Shekhtman, A. Goguet, R. Burch, C. Hardacre and N. Maguire, J. Catal., 2008, 253, 303 CrossRef CAS.
- J. Pérez-Ramírez, E. V. Kondratenko, G. Novell-Leruth and J. M. Ricar, J. Catal., 2009, 261, 225 Search PubMed.
- V. A. Kondratenko, Catal. Sci. Technol., 2015, 5, 1598 CAS.
- H.-J. Freund, H. Kuhlenbeck, J. Libuda, G. Rupprechter, M. Bäumer and H. Hamann, Top. Catal., 2001, 15, 201 CrossRef CAS.
- G. A. Somorjai, R. L. York, D. Butcher and J. Y. Park, Phys. Chem. Chem. Phys., 2007, 9, 3500 RSC.
- A. Goguet, F. Meunier, D. Tibiletti, J. P. Breen and R. Burch, J. Phys. Chem. B, 2004, 108, 20240 CrossRef CAS.
- F. Wang, R. Büchel, A. Savitsky, M. Zalibera, D. Widmann, S. E. Pratsinis, W. Lubitz and F. Schüth, ACS Catal., 2016, 6, 3520 CrossRef CAS.
- D. Widmann, A. Krautsieder, P. Walter, A. Brückner and R. J. Behm, ACS Catal., 2016, 6, 5005 CrossRef CAS.
- S. A. Theofanidis, R. Batchu, V. V. Galvita, H. Poelman and G. B. Marin, Appl. Catal., B, 2016, 185, 42 CrossRef CAS.
- P. Hu, Z. Huang, Z. Amghouz, M. Makkee, F. Xu, F. Kapteijn, A. Dikhtiarenko, Y. Chen, X. Gu and X. Tang, Angew. Chem., Int. Ed., 2014, 53, 3418 CrossRef CAS PubMed.
- S. A. Mavlyankariev, S. J. Ahlers, V. A. Kondratenko, D. Linke and E. V. Kondratenko, ACS Catal., 2016, 6, 3317 CrossRef CAS.
- S. J. Ahlers, U. Bentrup, D. Linke and E. V. Kondratenko, ChemSusChem, 2014, 7, 2631 CrossRef CAS PubMed.
- M. Moser, V. Paunović, Z. Guo, L. Szentmiklósi, M. G. Hevia, M. Higham, N. López, D. Teschner and J. Pérez-Ramírez, Chem. Sci., 2016, 7, 2996 RSC.
- E. A. Redekop, S. Saerens, V. V. Galvita, I. P. González, M. Sabbe, V. Bliznuk, M.-F. Reyniers and G. B. Marin, J. Catal., 2016, 344, 482 CrossRef CAS.
- D. Teschner, G. Novell-Leruth, R. Farra, A. Knop-Gericke, R. Schlögl, L. Szentmiklósi, M. G. Hevia, H. Soerijanto, R. Schomäcker, J. Pérez-Ramírez and N. López, Nat. Chem., 2012, 4, 739 CrossRef CAS PubMed.
- O. V. Buyevskaya, M. Rothaemel, H. W. Zanthoff and M. Baerns, J. Catal., 1994, 150, 71 CrossRef CAS.
- G. Creten, D. S. Lafyatis and G. F. Froment, J. Catal., 1995, 154, 151 CrossRef CAS.
- Y. Schuurman, A. Pantazidis and C. Mirodatos, Chem. Eng. Sci., 1999, 54, 3619 CrossRef CAS.
- T. A. Nijhuis, L. J. P. van den Broeke, M. J. G. Linders, J. M. van de Graaf, F. Kapteijn, M. Makkee and J. A. Moulijn, Chem. Eng. Sci., 1999, 54, 4423 CrossRef CAS.
- B. Kubias, U. Rodemerck, H. W. Zanthoff and M. Meisel, Catal. Today, 1996, 32, 243 CrossRef CAS.
- G. Creten, F.-D. Kopinke and G. F. Froment, Can. J. Chem. Eng., 1997, 75, 882 CrossRef CAS.
- M. Rothaemel, Transientenexperimente zur Aufklärung von Adsorptionsvorgängen und katalytischen Reaktionen an Festkörperoberflächen: Modellierung, Simulation und Experiment, PhD Thesis, Ruhr-Universität Bochum, 1995 Search PubMed.
- N. Maguire, A. Sasegbon, A. Abdelkader, A. Goguet, C. Hardacre, K. Hellgardt, K. Morgan and S. O. Shekhtman, Chem. Eng. Sci., 2013, 87, 224 CrossRef CAS.
- K. Morgan, TAP Reactor Development and Application in the Kinetic Characterization of Catalysts for Heterogeneously Catalyzed Gas Phase Reactions, PhD Thesis, Queen’s University Belfast, 2010 Search PubMed.
- E. V. Kondratenko, H. Wang, V. A. Kondratenko and J. Caro, J. Mol. Catal. A: Chem., 2009, 297, 142 CrossRef CAS.
- V. A. Kondratenko, C. Berger-Karin and E. V. Kondratenko, ACS Catal., 2014, 4, 3136 CrossRef CAS.
- T. Otroshchenko, S. Sokolov, M. Stoyanova, V. A. Kondratenko, U. Rodemerck, D. Linke and E. V. Kondratenko, Angew. Chem., Int. Ed., 2015, 54, 15880 CrossRef CAS PubMed.
- S. O. Shekhtman, G. S. Yablonsky, J. T. Gleaves and R. Fushimi, Chem. Eng. Sci., 2004, 59, 5493 CrossRef CAS.
- H. W. Zanthoff, S. A. Buchholz, A. Pantazidis and C. Mirodatos, Chem. Eng. Sci., 1999, 54, 4397 CrossRef CAS.
- H. W. Zanthoff, W. Grünert, S. Buchholz, M. Heber, L. Stievano, F. E. Wagner and G. U. Wolf, J. Mol. Catal. A: Chem., 2000, 162, 443 CrossRef.
- J. Pérez-Ramírez, E. V. Kondratenko, V. A. Kondratenko and M. Baerns, J. Catal., 2004, 227, 90 CrossRef.
- E. V. Kondratenko, V. A. Kondratenko, M. Richter and R. Fricke, J. Catal., 2006, 239, 23 CrossRef CAS.
- E. V. Kondratenko and J. Pérez-Ramírez, Appl. Catal., B, 2006, 64, 35 CrossRef CAS.
- K. Morgan, K. J. Cole, A. Goguet, C. Hardacre, G. J. Hutchings, N. Maguire, S. O. Shekhtman and S. H. Taylor, J. Catal., 2010, 276, 38 CrossRef CAS.
- N. C. Rigas, G. D. Svoboda and J. T. Gleaves, Activation of Silver Powder for Ethylene Epoxidation at Vacuum and Atmospheric Pressures in Catalytic Selective Oxidation, ed. S. T. Oyama and J. W. Hightower, American Chemical Society, Washington D.C., USA, 1993, vol. 523, p. 183 Search PubMed.
- O. Dewaele and G. F. Froment, Appl. Catal., A, 1999, 185, 203 CrossRef CAS.
- H. W. Zanthoff, S. A. Buchholz and O. Y. Ovsitser, Catal. Today, 1996, 32, 291 CrossRef CAS.
- D. Widmann and R. J. Behm, Angew. Chem., Int. Ed., 2011, 5, 10241 CrossRef PubMed.
- L. Wang, H. Jin, D. Widmann, J. Weissmüller and R. Behm, J. Catal., 2011, 278, 219 CrossRef CAS.
- D. Widmann and R. Behm, Acc. Chem. Res., 2014, 47, 740 CrossRef CAS PubMed.
- E. V. Kondratenko, Y. Sakamoto, K. Okumura and H. Shinjoh, Appl. Catal., B, 2009, 89, 476 CrossRef CAS.
- B. Solsona, T. García, G. J. Hutchings, S. H. Taylor and M. Makkee, Appl. Catal., A, 2009, 365, 222 CrossRef CAS.
- V. Balcaen, R. Roelant, H. Poelman, D. Poelman and G. Marin, Catal. Today, 2010, 157, 49 CrossRef CAS.
- U. Menon, V. V. Galvita and G. B. Marin, J. Catal., 2011, 283, 1 CrossRef CAS.
- O. Czuprat, J. Caro, V. A. Kondratenko and E. V. Kondratenko, Catal. Commun., 2010, 11, 1211 CrossRef CAS.
- A. Bueno-López, K. Krishna, B. van der Linden, G. Mul, J. Moulijn and M. Makkee, Catal. Today, 2007, 121, 237 CrossRef.
- U. Menon, H. Poelman, V. Bliznuk, V. V. Galvita, D. Poelman and G. B. Marin, J. Catal., 2012, 295, 91 CrossRef CAS.
- D. M. Gómez, V. V. Galvita, J. M. Gatica, H. Vidal and G. B. Marin, Phys. Chem. Chem. Phys., 2014, 16, 11447 RSC.
- Y. Hartadi, R. J. Behm and D. Widmann, Catalysts, 2016, 6, 21 CrossRef.
- D. Widmann, E. Hocking and R. Behm, J. Catal., 2014, 317, 272 CrossRef CAS.
- J. Pérez-Ramírez and E. V. Kondratenko, J. Catal., 2007, 250, 240 CrossRef.
- B. Beck, V. Fleischer, S. Arndt, M. G. Hevia, A. Urakawa, P. Hugo and R. Schomäcker, Catal. Today, 2014, 228, 212 CrossRef CAS.
- E. V. Kondratenko and M. Y. Sinev, Appl. Catal., A, 2007, 325, 353 CrossRef CAS.
- M. Olea, I. Sack, V. Balcaen, G. Marin, H. Poelman, K. Eufinger, D. Poelman, R. de Gryse, J. Paul and B. Sels, Appl. Catal., A, 2007, 318, 37 CrossRef CAS.
- E. Gubanova, A. van Veen, C. Mirodatos, V. Sadykov and N. Sazonova, Russ. J. Gen. Chem., 2008, 78, 2191 CrossRef CAS.
- A. P. Amrute, C. Mondelli, M. A. Hevia and J. Pérez-Ramírez, ACS Catal., 2016, 1, 583 CrossRef.
- M. A. Hevia, A. P. Amrute, T. Schmidt and J. Pérez-Ramírez, J. Catal., 2010, 276, 141 CrossRef CAS.
- A. P. Amrute, C. Mondelli, M. A. Hevia and J. Pérez-Ramírez, J. Phys. Chem. C, 2010, 115, 1056 Search PubMed.
- D. Teschner, R. Farra, L. Yao, R. Schlögl, H. Soerijanto, R. Schomäcker, T. Schmidt, L. Szentmiklósi, A. P. Amrute and C. Mondelli, J. Catal., 2012, 285, 273 CrossRef CAS.
- M. Olea, M. Tada and Y. Iwasawa, Top. Catal., 2007, 44, 137 CrossRef CAS.
- Q. Huynh, Y. Schuurman, P. Delichere, S. Loridant and J. Millet, J. Catal., 2009, 261, 166 CrossRef CAS.
- J. Pérez-Ramírez, E. V. Kondratenko, G. Novell-Leruth and J. M. Ricart, J. Catal., 2009, 261, 217 CrossRef.
- R. Imbihl, A. Scheibe, Y. Zeng, S. Günther, R. Kraehnert, V. Kondratenko, M. Baerns, W. Offermans, A. Jansen and R. van Santen, Phys. Chem. Chem. Phys., 2007, 9, 3522 RSC.
- C. Berger-Karin, J. Radnik and E. V. Kondratenko, J. Catal., 2011, 280, 116 CrossRef CAS.
- V. A. Kondratenko, G. Weinberg, M.-M. Pohl and D. S. Su, Appl. Catal., A, 2010, 381, 66 CrossRef CAS.
- V. A. Kondratenko, Appl. Catal., A, 2010, 381, 74 CrossRef CAS.
- S. Delagrange and Y. Schuurman, Catal. Today, 2007, 121, 204 CrossRef CAS.
- C. Berger-Karin, M. Sebek, M. M. Pohl, U. Bentrup, V. A. Kondratenko, N. Steinfeldt and E. V. Kondratenko, ChemCatChem, 2012, 4, 1368 CrossRef CAS.
- S. O. Shekhtman, G. S. Yablonsky, J. T. Gleaves and R. Fushimi, Chem. Eng. Sci., 2003, 58, 4843 CrossRef CAS.
- I.-C. Marcu, I. Sandulescu, Y. Schuurman and J.-M. M. Millet, Appl. Catal., A, 2008, 334, 207 CrossRef CAS.
- E. V. Kondratenko, V. A. Kondratenko, M. Santiago and J. Pérez-Ramírez, J. Catal., 2008, 256, 248 CrossRef CAS.
- E. V. Kondratenko and J. Pérez-Ramírez, Catal. Today, 2007, 119, 243 CrossRef CAS.
- E. V. Kondratenko and J. Pérez-Ramírez, Catal. Today, 2007, 121, 197 CrossRef CAS.
- E. V. Kondratenko, V. A. Kondratenko, M. Santiago and J. Pérez-Ramírez, Appl. Catal., B, 2010, 99, 66 CrossRef CAS.
- V. Medhekar, V. Balakotaiah and M. P. Harold, Catal. Today, 2007, 121, 226 CrossRef CAS.
- V. A. Kondratenko, U. Bentrup, M. Richter, T. W. Hansen and E. V. Kondratenko, Appl. Catal., B, 2008, 84, 497 CrossRef CAS.
- A. Kumar, X. Zheng, M. P. Harold and V. Balakotaiah, J. Catal., 2011, 279, 12 CrossRef CAS.
- A. Kumar, M. P. Harold and V. Balakotaiah, J. Catal., 2010, 270, 214 CrossRef CAS.
- B. Bachiller-Baeza, C. Mateos-Pedrero, M. Soria, A. Guerrero-Ruiz, U. Rodemerck and I. Rodríguez-Ramos, Appl. Catal., B, 2013, 129, 450 CrossRef CAS.
- C. Breitkopf, ChemCatChem, 2009, 1, 259 CrossRef CAS.
- S. O. Shekhtman, G. S. Yablonsky, S. Chen and J. T. Gleaves, Chem. Eng. Sci., 1999, 54, 4371 CrossRef CAS.
- G. S. Yablonsky, Theor. Found. Chem. Eng., 2014, 48, 608 CrossRef CAS.
- X. Zheng, G. M. Veith, E. Redekop, C. S. Lo, G. S. Yablonsky and J. T. Gleaves, Ind. Eng. Chem. Res., 2010, 49, 10428 CrossRef CAS.
- M. P. Lobera, G. Biausque, C. Tellez, J. Herguido, M. Menendez and Y. Schuurman, Chem. Eng. Sci., 2010, 65, 2417 CrossRef CAS.
- J. Schaeffer, V. A. Kondratenko, N. Steinfeldt, M. Sebek and E. V. Kondratenko, J. Catal., 2013, 301, 210 CrossRef CAS.
- V. Balcaen, I. Sack, M. Olea and G. B. Marin, Appl. Catal., A, 2009, 371, 31 CrossRef CAS.
- M. Santiago, V. Kondratenko, E. Kondratenko, N. Lopez and J. Pérez-Ramírez, Appl. Catal., B, 2011, 110, 33 CrossRef CAS.
- K. Morgan, B. Inceesungvorn, A. Goguet, C. Hardacre, F. C. Meunier and S. O. Shekhtman, Catal. Sci. Technol., 2012, 2, 2128 CAS.
- K. S. Kabin, P. Khanna, R. L. Muncrief, V. Medhekar and M. P. Harold, Catal. Today, 2006, 114, 72 CrossRef CAS.
- A. Kumar, V. Medhekar, M. P. Harold and V. Balakotaiah, Appl. Catal., B, 2009, 90, 642 CrossRef CAS.
- R. Feres, A. Cloninger, G. S. Yablonsky and J. T. Gleaves, Chem. Eng. Sci., 2009, 64, 4358 CrossRef CAS.
- R. Leppelt, D. Hansgen, D. Widmann, T. Häring, G. Bräth and R. J. Behm, Rev. Sci. Instrum., 2007, 78, 104103 CrossRef CAS PubMed.
- L. C. Wang, Y. Zhong, D. Widmann, J. Weissmüller and R. J. Behm, ChemCatChem, 2012, 4, 251 CrossRef CAS.
- L. C. Wang, D. Widmann and R. J. Behm, Catal. Sci. Technol., 2015, 5, 925 CAS.
- T. A. Nijhuis, L. J. P. van den Broeke, M. J. G. Linders, M. Makkee, F. Kapteijn and J. A. Moulijn, Catal. Today, 1999, 53, 189 CrossRef CAS.
- A. C. van Veen, D. Farrusseng, M. Rebeilleau, T. Decamp, A. Holzwarth, Y. Schuurman and C. Mirodatos, J. Catal., 2003, 216, 135 CrossRef CAS.
- B. A. Mamyrin, Int. J. Mass Spectrom., 2001, 206, 251 CrossRef CAS.
- H. T. Randall, P. L. Mills and J. S. McCracken, Stud. Surf. Sci. Catal., 1999, 122, 209 CrossRef CAS.
- A. Goguet, C. Hardacre, N. Maguire, K. Morgan, S. O. Shekhtman and S. P. Thompson, Analyst, 2011, 136, 155 RSC.
- F. Xian, C. L. Hendrickson and A. G. Marshall, Anal. Chem., 2012, 84, 708 CrossRef CAS PubMed.
- P. Phanawadee, S. O. Shekhtman, C. Jarungmanorom, G. S. Yablonsky and J. T. Gleaves, Chem. Eng. Sci., 2003, 58, 2215 CrossRef CAS.
- S. Pietrzyk, E. Redekop, G. Yablonsky and G. B. Marin, Chem. Eng. Sci., 2015, 134, 367 CrossRef CAS.
- M. Suzuki and J. M. Smith, AIChE J., 1972, 18, 326 CrossRef CAS.
- P. A. Ramachandran and J. M. Smith, Ind. Eng. Chem. Fundam., 1978, 17, 148 CAS.
- S. O. Shekhtman and G. S. Yablonsky, Ind. Eng. Chem. Res., 2005, 44, 6518 CrossRef CAS.
- S. C. van der Linde, T. A. Nijhuis, F. H. M. Dekker, F. Kapteijn and J. A. Moulijn, Appl. Catal., A, 1997, 151, 27 CrossRef CAS.
- V. Fierro, J. L. Duplan, J. Verstraete, Y. Schuurman and C. Mirodatos, A non-stationary kinetic approach of the determination of the kinetic parameters of the protolytic cracking of methylcyclohexane in Reaction kinetics and the development of catalytic processes, ed. G. F. Froment and K. C. Waugh, Elsevier Science B.V., Amsterdam, The Netherlands, 2001, vol. 133, pp. 341–348 Search PubMed.
- R. J. Berger, F. Kapteijn, J. A. Moulijn, G. B. Marin, J. de Wilde, M. Olea, D. Chen, A. Holmen, L. Lietti, E. Tronconi and Y. Schuurman, Appl. Catal., A, 2008, 342, 3 CrossRef CAS.
- R. Roelant, D. Constales, R. van Keer and G. B. Marin, Chem. Eng. Sci., 2008, 63, 1850 CrossRef CAS.
- E. V. Kondratenko, M. Schlueter, M. Baerns, D. Linke and M. Holena, Catal. Sci. Technol., 2015, 5, 1668 CAS.
- M. Rothaemel and M. Baerns, Ind. Eng. Chem. Res., 1996, 35, 1556 CrossRef CAS.
- M. Soick, D. Wolf and M. Baerns, Chem. Eng. Sci., 2000, 55, 2875 CrossRef CAS.
- G. Yablonsky, E. Redekop, D. Constales, J. T. Gleaves and G. B. Marin, Int. J. Chem. Kinet., 2016, 48, 304 CrossRef CAS.
- D. Constales, G. S. Yablonsky and G. B. Marin, Math. Modell. Nat. Phenom., 2015, 10, 119 CrossRef.
- D. Constales, G. S. Yablonsky, P. Phanawadee, N. Pongboutr, J. Limtrakul and G. B. Marin, AIChE J., 2015, 61, 31 CrossRef CAS.
- C. Breitkopf and U. Sénéchal, Heat Mass Transfer, 2014, 50, 393 CrossRef.
- P. Phanawadee, N. Pongboutr, G. S. Yablonsky, D. Constales, C. Jarungmanorom, W. Soikham and J. Limtrakul, AIChE J., 2013, 59, 3574 CrossRef CAS.
- G. S. Yablonsky, S. O. Shekhtman, P. Phanawadee and J. T. Gleaves, Catal. Today, 2001, 64, 227 CrossRef CAS.
- D. Constales, G. S. Yablonsky, G. B. Marin and J. T. Gleaves, Chem. Eng. Sci., 2001, 56, 133 CrossRef CAS.
- D. Constales, G. S. Yablonsky, G. B. Marin and J. T. Gleaves, Chem. Eng. Sci., 2001, 56, 1913 CrossRef CAS.
- D. Constales, G. S. Yablonsky, G. B. Marin and J. T. Gleaves, Chem. Eng. Sci., 2004, 59, 3725 CrossRef CAS.
- D. Constales, S. O. Shekhtman, G. S. Yablonsky, G. B. Marin and J. T. Gleaves, Chem. Eng. Sci., 2006, 61, 1878 CrossRef CAS.
- R. Feres and G. S. Yablonsky, Chem. Eng. Sci., 2004, 59, 1541 CrossRef CAS.
- R. Feres and G. S. Yablonsky, Chem. Eng. Sci., 2006, 61, 7864 CrossRef CAS.
- G. S. Yablonsky, D. Constales, S. Shekhtman and J. Gleaves, Chem. Eng. Sci., 2007, 62, 6754 CrossRef CAS.
- E. A. Redekop, G. S. Yablonsky, D. Constales, P. A. Ramachandran, C. Pherigo and J. T. Gleaves, Chem. Eng. Sci., 2011, 66, 6441 CrossRef CAS.
- M. Filez, E. A. Redekop, V. V. Galvita, H. Poelman, M. Meledina, S. Turner, G. van Tendeloo, A. T. Bell and G. B. Marin, Phys. Chem. Chem. Phys., 2016, 18, 3234 RSC.
- E. A. Redekop, G. S. Yablonsky, D. Constales, P. A. Ramachandran, J. T. Gleaves and G. B. Marin, Chem. Eng. Sci., 2014, 110, 20 CrossRef CAS.
- A. Goguet, C. Hardacre, B. Inceesungvorn, K. Morgan and S. O. Shekhtman, Catal. Sci. Technol., 2011, 1, 760 Search PubMed.
- E. A. Redekop, G. S. Yablonsky, V. V. Galvita, D. Constales, R. Fushimi, J. T. Gleaves and G. B. Marin, Ind. Eng. Chem. Res., 2013, 52, 15417 CrossRef CAS.
- B. C. Gates, Catalysis on Surfaces in Catalytic Chemistry, John Wiley and Sons, Inc., New York, USA, 1992, pp. 310–421 Search PubMed.
- F. H. Ribeiro, A. E. S. von Wittenau, C. H. Bartolomew and G. A. Somorjai, Catal. Rev.: Sci. Eng., 1997, 39, 49 CAS.
- J. Happel, Chem. Eng. Sci., 1978, 33, 1567 CrossRef CAS.
- J. Happel, H. Y. Chen, M. Otarod, S. Otaya, A. J. Severdia, T. Yoshida and V. Fthenakis, J. Catal., 1982, 75, 314 CrossRef CAS.
- C. O. Bennett, Understanding heterogeneous catalysis through the transient method in Catalysis Under Transient Conditions, ed. A. T. Bell, L. Hegedus and M. J. Comstock, American Chemical Society, Washington D.C., Series edn, 1982, vol. 178, pp. 1–32 Search PubMed.
- P. Biloen, J. Mol. Catal., 1983, 21, 17 CrossRef CAS.
- J. G. Goodwin Jr., S. Kim and W. D. Rhodes, Turnover frequencies in metal catalysis: Meanings, functionalities and relationships in Catalysis: Volume 17, ed. J. J. Spivey and G. W. Roberts, The Royal Society of Chemistry, Cambridge, UK, 2004, pp. 320–347 Search PubMed.
- K. Morgan, A. Goguet, C. Hardacre, E. V. Kondratenko, C. McManus and S. O. Shekhtman, Catal. Sci. Technol., 2014, 4, 3665 CAS.
- N. E. McGuire, N. P. Sullivan, O. Deutschmann, H. Zhu and R. J. Kee, Appl. Catal., A, 2011, 394, 257 CrossRef CAS.
- W. P. Partridge, J. M. E. Storey, S. A. Lewis, R. W. Smithwick, G. L. DeVault, M. J. Cunningham, N. V. Currier and T. M. Yonushonis, SAE Technical Paper, 2000, 2000-01-2952 Search PubMed.
- J. Sá, D. L. Fernandes, F. Aiouache, A. Goguet, C. Hardacre, D. Lundie, W. Naeem, W. P. Partridge and C. Stere, Analyst, 2010, 135, 2260 RSC.
- G. S. Bugosh, V. G. Easterling, I. A. Rusakova and M. P. Harold, Appl. Catal., B, 2015, 165, 68 CrossRef CAS.
- J. Touitou, K. Morgan, R. Burch, C. Hardacre and A. Goguet, Catal. Sci. Technol., 2012, 2, 1811 CAS.
- J. Touitou, R. Burch, C. Hardacre, C. McManus, K. Morgan, J. Sá and A. Goguet, Analyst, 2013, 138, 2858 RSC.
- J. Touitou, F. Aiouache, R. Burch, R. Douglas, C. Hardacre, K. Morgan, J. Sá, C. Stewart, J. Stewart and A. Goguet, J. Catal., 2014, 319, 239 CrossRef CAS.
- D. Farrusseng, C. Daniel, C. Gaudillère, U. Ravon, Y. Schuurman, C. Mirodatos, D. Dubbeldam, H. Frost and R. Q. Snurr, Langmuir, 2009, 25, 7383 CrossRef CAS PubMed.
- M. Kuniavsky, Introduction: The middle of Moore’s Law in Smart Things, Elsevier, Burlington, MA 01803, USA, 2010, pp. 3–11 Search PubMed.
- D. Constales, G. S. Yablonsky, L. Wang, W. Diao, V. V. Galvita and R. Fushimi, Catal. Today, 2017 DOI:10.1016/j.cattod.2017.04.036.
- S. P. Thompson, personal communication to AG, Scientific Analysis Instruments Ltd, Manchester, UK, 2016 Search PubMed.
- C. Freitag, S. Besselmann, E. Löffler, W. Grünert, F. Rosowski and M. Muhler, Catal. Today, 2004, 91–92, 143 CrossRef CAS.
- D. J. Statman, J. T. Gleaves, D. McNamara, P. L. Mills, G. Fornasari and J. R. H. Ross, Appl. Catal., 1991, 77, 45 CrossRef CAS.
- D. R. Coulson, P. L. Mills, K. Kourtakis, P. W. J. G. Wijnen, J. J. Lerou and L. E. Manzer, Stud. Surf. Sci. Catal., 1993, 75, 2015 CrossRef CAS.
- G. D. Svoboda, J. T. Gleaves and P. L. Mills, Stud. Surf. Sci. Catal., 1994, 82, 481 CrossRef CAS.
- B. S. Zou, M. P. Dudukovic and P. L. Mills, J. Catal., 1994, 148, 683 CrossRef CAS.
- R. Y. Brogaard, R. Henry, Y. Schuurman, A. J. Medford, P. G. Moses, P. Beato, S. Svelle, J. K. Nørskov and U. Olsbye, J. Catal., 2014, 314, 159 CrossRef CAS.
- G. P. Ansell, A. F. Diwell, S. E. Golunski, J. W. Hayes, R. R. Rajaram, T. J. Truex and A. P. Walker, Appl. Catal., B, 1993, 2, 81 CrossRef CAS.
- R. Burch, P. J. Millington and A. P. Walker, Appl. Catal., B, 1994, 4, 65 CrossRef CAS.
- G. P. Ansell, S. E. Golunski, J. W. Hayes, A. P. Walker, R. Burch and P. J. Millington, Stud. Surf. Sci. Catal., 1995, 96, 577 CrossRef CAS.
- A. N. J. van Keulen, K. Seshan, J. H. B. J. Hoebink and J. R. H. Ross, J. Catal., 1997, 166, 306 CrossRef CAS.
- G. Centi, F. Trifirò, G. Busca, J. Ebner and J. Gleaves, Faraday Discuss. Chem. Soc., 1989, 87, 215 RSC.
- J. T. Gleaves, A. G. Sault, R. J. Madix and J. R. Ebner, J. Catal., 1990, 121, 202 CrossRef CAS.
- W. R. Moser, G. A. Rossetti Jr., J. T. Gleaves and J. R. Ebner, J. Catal., 1991, 127, 190 CrossRef CAS.
- J. P. Huinink, J. H. B. J. Hoebink and G. B. Marin, Can. J. Chem. Eng., 1996, 74, 580 CrossRef CAS.
- J. H. B. J. Hoebink, J. P. Huinink and G. B. Marin, Appl. Catal., A, 1997, 160, 139 CrossRef CAS.
- Y. Sakamoto, S. Matsunaga, K. Okumura, T. Kayama, K. Yamazaki, N. Takahashi, T. Tanaka, Y. Kizaki, T. Motohiro and H. Shinjoh, Chem. Eng. Sci., 2008, 63, 5028–5034 CrossRef CAS.
- Y. Sakamoto, S. Matsunaga, K. Okumura, T. Kayama, K. Yamazaki, N. Takahashi, T. Tanaka, Y. Kizaki, T. Motohiro and H. Shinjoh, Appl. Catal., A, 2012, 445–446, 133 CrossRef CAS.
- Y. Wang, J. Posthuma de Boer, F. Kapteijn and M. Makkee, ChemCatChem, 2016, 8, 102 CrossRef CAS.
- Y. Wang, J. Posthuma de Boer, F. Kapteijn and M. Makkee, Top. Catal., 2016, 59, 854 CrossRef CAS.
- Y. Renème, S. Pietrzyk, F. Dhainaut, M. Chaar, A. C. van Veen and P. Granger, Front. Chem., 2016, 4, 7 Search PubMed.
- R. B. Duarte, M. Olea, E. Iro, T. Sasaki, K. Itako and J. A. van Bokhoven, ChemCatChem, 2014, 6, 2898 CrossRef CAS.
- P. Granger and S. Pietrzyk, C. R. Chim., 2014, 17, 656 CrossRef CAS.
- S. Roy and A. Baiker, Chem. Rev., 2009, 109, 4054 CrossRef CAS PubMed.
- J. T. Gleaves, G. S. Yablonskii, P. Phanawadee and Y. Schuurman, Stud. Surf. Sci. Catal., 1997, 109, 333 CrossRef CAS.
- A. Akram, S. J. Freakley, C. Reece, M. Piccinini, G. Shaw, J. K. Edwards, F. Desmedt, P. Miquel, E. Seuna, D. J. Willock, J. A. Moulijn and G. J. Hutchings, Chem. Sci., 2016, 7, 5833 RSC.
- A. Goguet, W. P. Partridge, F. Aiouache, C. Hardacre, K. Morgan, J. Sá and C. Stere, Catal. Today, 2014, 236, 206 CrossRef CAS.
- U. Menon, V. V. Galvita, D. Constales, K. Alexopoulos, G. Yablonsky and G. B. Marin, Catal. Today, 2015, 258, 214 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2017 |