Hydrogenolysis of alkanes: reactions of n-butane on Ru/zeolite catalysts
Abstract
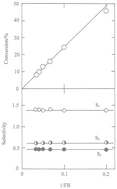
Ru/13X zeolite catalysts containing 0.6, 2 and 5.7% Ru prepared by reduction or decomposition of the hexammine complex are active and stable for n-butane hydrogenolysis between 400 and 460 K, and show similar activation energies (150–160 kJ mol−1) and orders of reaction (−1.5 to −2 in H2; 0.5–0.65 in n-butane); product selectivities show weak dependence on temperature and H2 pressure, with preference for terminal bond scission. Oxidising either the decomposed or the reduced catalysts gave a marked increase in activity, a lower activation energy (120–130 kJ mol−1), higher orders of reaction in H2 (∼−0.9), lower orders in n-butane (∼0.2) and product selectivities that showed greater change with temperature and H2 pressure; terminal bond scission was >90%. The change in character with oxidation was attributed to weaker H2 chemisorption and a higher concentration of partially dehydrogenated C4 species; the active phase may consist of very small particles of RuO2 confined within the supercages of the zeolite.
- This article is part of the themed collection: Catalytic reactivity of surfaces: in recognition of François Gault

 Please wait while we load your content...
Please wait while we load your content...