Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Addressing stability challenges of using bimetallic electrocatalysts: the case of gold–palladium nanoalloys†
Enrico
Pizzutilo
 *a,
Simon J.
Freakley
b,
Simon
Geiger
a,
Claudio
Baldizzone
a,
Andrea
Mingers
a,
Graham J.
Hutchings
*a,
Simon J.
Freakley
b,
Simon
Geiger
a,
Claudio
Baldizzone
a,
Andrea
Mingers
a,
Graham J.
Hutchings
 b,
Karl J. J.
Mayrhofer
acd and
Serhiy
Cherevko
*ac
b,
Karl J. J.
Mayrhofer
acd and
Serhiy
Cherevko
*ac
aDepartment of Interface Chemistry and Surface Engineering, Max-Planck-Institut für Eisenforschung GmbH, Max-Planck-Strasse 1, 40237 Düsseldorf, Germany. E-mail: pizzutilo@mpie.de; Fax: +49 211 6792 218; Tel: +49 211 6792 160
bCardiff Catalysis Institute, School of Chemistry, Cardiff University, Main Building, Park Place, Cardiff, CF10 3AT, UK
cForschungszentrum Jülich GmbH, Helmholtz Institute Erlangen-Nürnberg for Renewable Energy (IEK-11), Egerlandstr. 3, 91058 Erlangen, Germany. E-mail: s.cherevko@fz-juelich.de
dDepartment of Chemical and Biological Engineering, Friedrich-Alexander-Universität Erlangen-Nürnberg, Egerlandstr. 3, 91058 Erlangen, Germany
First published on 22nd March 2017
Abstract
Bimetallic catalysts are known to often provide enhanced activity compared to pure metals, due to their electronic, geometric and ensemble effects. However, applied catalytic reaction conditions may induce re-structuring, metal diffusion and dealloying. This gives rise to a drastic change in surface composition, thus limiting the application of bimetallic catalysts in real systems. Here, we report a study on dealloying using an AuPd bimetallic nanocatalyst (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 molar ratio) as a model system. The changes in surface composition over time are monitored in situ by cyclic voltammetry, and dissolution is studied in parallel using online inductively coupled plasma mass spectrometry (ICP-MS). It is demonstrated how experimental conditions such as different acidic media (0.1 M HClO4 and H2SO4), different gases (Ar and O2), upper potential limit and scan rate significantly affect the partial dissolution rates and consequently the surface composition. The understanding of these alterations is crucial for the determination of fundamental catalyst activity, and plays an essential role for real applications, where long-term stability is a key parameter. In particular, the findings can be utilized for the development of catalysts with enhanced activity and/or selectivity.
1 molar ratio) as a model system. The changes in surface composition over time are monitored in situ by cyclic voltammetry, and dissolution is studied in parallel using online inductively coupled plasma mass spectrometry (ICP-MS). It is demonstrated how experimental conditions such as different acidic media (0.1 M HClO4 and H2SO4), different gases (Ar and O2), upper potential limit and scan rate significantly affect the partial dissolution rates and consequently the surface composition. The understanding of these alterations is crucial for the determination of fundamental catalyst activity, and plays an essential role for real applications, where long-term stability is a key parameter. In particular, the findings can be utilized for the development of catalysts with enhanced activity and/or selectivity.
1 Introduction
Since its discovery, gold catalysis has received ever-increasing interest and recently was proven to be a very successful tool for organic synthesis.1–5 In electrochemistry, gold has been commonly used as an electrode for various applications and fundamental studies thanks to its chemical inertness in the stability potential window of water and resistance to oxide formation. The “revival” of gold has attracted attention in the electrocatalysis community, as it reveals interesting activity for carbon monoxide oxidation, alcohol oxidation and oxygen reduction reaction.6 In most of its applications, gold is typically considered to be completely stable, however dissolution cannot always be neglected.7Recent work on heterogeneous catalysis showed that the addition of palladium to gold leads to activity or selectivity enhancement in several reactions1,8–12 (alcohol oxidation, H2O2 synthesis, toluene oxidation to benzoyl benzoate, methane oxidation with H2O2), and led to new exciting catalyst developments based on bimetallic nanoparticle catalysts. Over the last few years, gold–palladium alloys have also been commonly studied in electrocatalysis, i.e. as catalysts for the oxygen reduction reaction,13–16 hydrogen peroxide synthesis and reduction,17–19 ethanol oxidation20–22 and methanol oxidation.23 In homogeneous catalysis, the transmetalation from gold to palladium, in order to combine the typical gold-catalyzed cycloisomerization with additional C–C cross-coupling,8,24–26 has also been studied computationally in great detail.27
It is known that bimetallic catalysts often provide enhanced activity compared to their pure counterparts and many recent studies have focused particularly on this topic. The superior activity can result from three different effects. (I) The electronic or ligand effect causes changes in the band structure, thus influencing the strength of binding between the metal surface and adsorbate molecules.28–30 (II) The geometric effect produces surface strain as a consequence of the atomic arrangement of surface atoms to reduce the lattice mismatch.31,32 (III) An ensemble effect arises when individual or small groups (ensembles) of different metal atoms on the surface act as preferential active sites available to adsorbates.33,34 Indeed, the co-presence of both metals impacts the reaction rates and kinetics. Among others, this is particularly relevant for applications such as hydrogen peroxide synthesis (AuPd,1,17,18,35 PtHg,36 PdHg37), CO oxidation (AuPd38), ethanol oxidation (AuPd39), methanol oxidation (Pt–M40) and formic acid oxidation (Pt–M41,42).
The surface compositions along with the surface atomic arrangement in bimetallic nanoparticles play an extremely important role and are often crucial for high reactivity.17,22,43,44 However, despite the great excitement around these catalysts, it is a great challenge to control activity over extended times only by tuning the composition and structure during synthesis. Indeed, the reaction environment and the applied conditions45–47 play a key role in the stability and thus the success and future application of bimetallic catalysts. Metal migration and surface segregation,39 as well as dissolution and dealloying,48–50 can induce alterations in the surface composition and consequently in the activity over time.
Particularly, dissolution is an important factor that needs to be considered in studies of solid–liquid interfaces, although typical rates of noble-metal dissolution are relatively low. However, they can be relevant over long periods (years) that these catalysts are in operation and as a consequence in economic considerations.51 Moreover, one needs to be aware of the extent of dissolution during short-term kinetic studies, as even minor surface changes can have severe impact.
The development of a unique experimental technique that combines online inductively coupled plasma mass spectrometry (ICP-MS) with an analytics electrochemical scanning flow cell (SFC)52,53 has permitted the time-resolved quantification of low amounts of dissolved elements during catalytic studies, and thus significantly contributed to fundamental understanding of dissolution/degradation processes, like the dissolution of bulk (foil or disk) noble metals,54 including different studies on gold7,55 and palladium.56 While polycrystalline bulk materials constitute model systems for understanding the fundamental dissolution mechanisms, the stability of real-application high surface area catalysts has not been comprehensively investigated.57 Furthermore, due to the complexity of the alloy interface, the number of studies on bimetallic nanoparticle dissolution is limited.48,58,59
In this work, we report a time-resolved dissolution study on gold–palladium bimetallic nanoparticles supported directly onto an electrode. These were originally designed and synthesized for hydrogen peroxide production for which, as mentioned above, the ensemble effect is of crucial importance. In particular, the dissolution onset potential, the effect of the upper potential limit, the scan rate and the influence of the reaction environment (different acidic media and gases) will be presented and discussed.
2 Experimental
2.1 Nanoparticle synthesis and characterization
Au–Pd colloidal materials (Au, AuPd and Pd) were prepared following ref. 35. Initially, aqueous solutions of the desired concentration of NaBH4 (0.1 M), poly(vinyl alcohol) (PVA) (1 wt% aqueous solution, Aldrich, MW = 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000, 80% hydrolyzed), aqueous solutions of HAuCl4 (12.25 mg Au/ml, Johnson Matthey) and PdCl2 (6 mg Pd/ml, Johnson Matthey) were prepared. The PVA solution (1 wt%) was added with the following required amount (PVA/(Au + Pd) (w/w) = 1.2). Finally, the freshly prepared NaBH4 solution was added (0.1 M, NaBH4/(Au + Pd) (mol/mol) = 5) yielding, after 30 min of reaction, a dark-brown sol. The obtained solutions were concentrated using a rotary evaporator obtaining the Au, Pd and AuPd solutions with a concentration of 0.1 mg ml−1.
000, 80% hydrolyzed), aqueous solutions of HAuCl4 (12.25 mg Au/ml, Johnson Matthey) and PdCl2 (6 mg Pd/ml, Johnson Matthey) were prepared. The PVA solution (1 wt%) was added with the following required amount (PVA/(Au + Pd) (w/w) = 1.2). Finally, the freshly prepared NaBH4 solution was added (0.1 M, NaBH4/(Au + Pd) (mol/mol) = 5) yielding, after 30 min of reaction, a dark-brown sol. The obtained solutions were concentrated using a rotary evaporator obtaining the Au, Pd and AuPd solutions with a concentration of 0.1 mg ml−1.
The molar ratio of the AuPd sample was evaluated by ICP-MS before and after electrochemical measurements. The as-prepared or degraded catalysts were first dissolved in aqua regia (HNO3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) HCl (1
HCl (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3)) and then the obtained solutions were diluted in ultrapure water (UPW) in order to be measured using ICP-MS.
3)) and then the obtained solutions were diluted in ultrapure water (UPW) in order to be measured using ICP-MS.
Samples of the three different catalysts were prepared for examination by transmission electron microscopy (TEM) by dispersing the as-prepared sol gel solutions onto a lacey carbon film supported by a gold TEM grid (PLANO). To determine their particle sizes and composition, the prepared samples were then subjected to bright field contrast imaging and X-ray energy-dispersive spectrometry (XEDS) experiments using a JEOL 2200FS TEM operating at 200 kV.
The electrode used for the scanning flow cell (SFC) consisted of circular spots of catalyst that were printed onto glassy carbon plates starting from colloidal ink using a drop-on-demand printer (Nano-PlotterTM 2.0, GeSim). Each layer consisted of 200 drops. Single drops (volume = 150–200 pl) were dropped in rapid succession using a piezoelectric pipette. Only one layer was used for all experiments, apart from the estimation of the dissolution onset potential where 4 layers were used.
2.2 Electrochemical characterization
All electrochemical dissolution experiments were performed in an SFC similar to the one used in our previous work.52 The electrolytes were gas (Ar or O2)-purged 0.1 M H2SO4 and 0.1 M HClO4, prepared by dilution of concentrated acid (Suprapur®, Merck) in UPW (PureLab Plus system, Elga, 18 MΩ). The prepared catalyst films, a graphite rod and Ag/AgCl were used as the working (WE), counter (CE) and reference electrode (RE), respectively. Experimental parameters were controlled with homemade LabVIEW software. The flow rate of the electrolyte was 193 μl min−1. The quantitative analysis of the electrolyte for the dissolved 197Au and for 106Pd was performed with an ICP-MS (NexION 300X, Perkin Elmer), using as internal standards 187Re and 103Rh, respectively.The influence of degradation on the oxide reduction peaks was studied with a rotating disk electrode (RDE) method in the two considered electrolytes. A home-built three electrode separate compartment electrochemical cell made of Teflon® was employed. The working electrode consisted of 2 μg of catalyst deposited onto a polished home-made Teflon tip with a glassy carbon disk (5 mm from MaTecK). A graphite rod and Ag/AgCl were used as the CE and RE, respectively.
All experiments were carried out at room temperature (approximately 24 °C) and all the potentials reported in this work are referred to the reversible hydrogen electrode (RHE), which was measured for every experiment.
3 Results and discussion
A sol-immobilization method commonly employed in recent works35 was used to prepare colloidal solutions of unsupported Au, Pd and AuPd (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 molar ratio) catalysts. The latter consists of a bimetallic random homogeneous gold–palladium alloy with a face-centered cubic (fcc) structure as described in a previous publication.35
1 molar ratio) catalysts. The latter consists of a bimetallic random homogeneous gold–palladium alloy with a face-centered cubic (fcc) structure as described in a previous publication.35
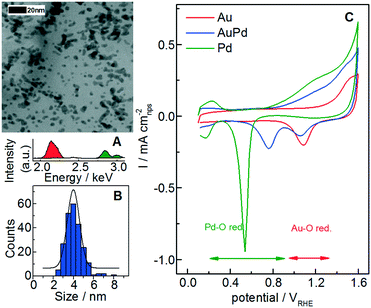
Representative bright field STEM micrographs (AuPd in Fig. 1A) of nanoparticles deposited onto a lacey carbon gold-coated TEM grid were acquired, in order to measure the average particle size and the size distribution (Fig. 1B and summary in Table 1). The AuPd alloy composition was furthermore qualitatively confirmed by energy-dispersive X-ray spectrometry (Fig. 1A) and by ICP-MS analysis of the as-synthesized AuPd catalyst.
| Median/nm | Mean/nm | St. dev. | ECSAa/m2 g−1 | A t (1l)b/mm2 | |
|---|---|---|---|---|---|
| a ECSA refers to the catalyst specific surface area, which was calculated from the particle mean size (for more information, see S2). b A t refers to the total surface area per deposited layer (≈2 ng). | |||||
| Au | 4.2 | 4.6 | ±2.1 | 68 | 0.14 |
| AuPd | 4.1 | 4.1 | ±0.8 | 92 | 0.18 |
| Pd | 3.1 | 3.2 | ±1.1 | 150 | 0.31 |
The prepared catalyst colloidal ink is printed on a glassy carbon plate, resulting in an array of samples that can be measured using a scanning flow cell (SFC) with an opening of around 1 mm in diameter. The loading of a single printed layer is estimated from the droplet size and is approximately 2 ng. From the statistical average particle size and loading, the total surface area per deposited layer is calculated (At in Table 1; see calculation in S1 and S2 of the ESI†).
Prior to dissolution studies, argon background CVs are measured up to 1.6 VRHE with a scan rate of 200 mV s−1 in 0.1 M HClO4 (perchloric acid) to characterize the freshly prepared samples (Fig. 1C). High potentials (1.6 VRHE) are used here and in other measurements of this work due to the Au oxide reduction peak that is only accessible at high upper limit potentials (ULP > 1.5 VRHE).55 The peak potential of the Pd oxide reduction shifts to higher potentials when Pd is alloyed with Au, in accordance with previous works on AuPd alloys.17,60–62 A shift to lower potentials is also observed for the Au oxide reduction and this depends on the composition;17 however, according to the literature, this shift is less pronounced compared to that for the Pd oxide reduction.62 Analyzing these features, it might be possible to derive the real electroactive surface areas of Au and Pd separately, i.e. by using (I) the charge under the oxide reduction peak,62 (II) the charge under the oxide formation peak or (III) the charge of the hydrogen underpotential deposition (HUPD).63 However, the estimation of the reduction peak for palladium, where different oxidized states are formed,61 and in general for alloys is challenging.60,62 Furthermore, the presence of gold is reported to hinder the hydrogen bulk absorption and surface adsorption/desorption features17 as well as the Pd-oxide reduction.60 Finally, in both cases, the integration of the charge could be affected by systematic errors related to the definition of the baseline. Therefore, we consider for these catalysts only the total surface area At calculated from the statistical particle size and loading (Table 1) as carried out also for Au–Pd catalysts in ref. 17. For AuPd, this value is in the same order of magnitude (within the error) with the initial surface area estimated from the double layer capacity (see Fig. S2 in the ESI†).
3.1 Dissolution onset potential
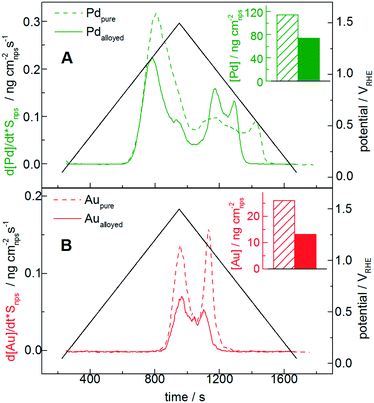
The transient dissolution of Au, Pd and AuPd alloy is studied by utilizing SFC-ICP-MS (Fig. 2). For this measurement, 4 printed catalyst layers are used to better identify the dissolution onset potentials, since the deviation from the background signal is easier to be observed when more catalyst is used. Note that the number of layers can influence the specific dissolution,64 whereas it does not influence the onset potential. The Au and Pd dissolutions during dynamic potential operation are initiated by the formation of the respective surface oxides as confirmed from the first CV of a freshly printed catalyst (Fig. 1). Only the first cycle is reported here, and for this measurement the dissolution is normalized to the surface area (At in Table 1); note that for the following Fig. 3 and 4 the dissolution is not normalized, since during a degradation measurement the nanoparticle surface area and its composition are steadily changing.For a better comparison with the pure metal counterparts in Fig. 2A and B, Au and Pd dissolutions are shown separately: the full and the dotted lines represent the alloy and the pure metal, respectively. The measured dissolution onset potentials are defined as the deviation from the background signal in the positive scan (see section S3 in the ESI†). Their values are ≈0.78 VRHE for pure Pd and ≈1.3 VRHE for pure Au. The value for pure Pd is in accordance with measurements on the polycrystalline bulk metal, while a previous study on polycrystalline Au in perchloric acid showed values slightly higher than those for our Au nanoparticles.54 In Fig. 2B, the gold profile presents the two typical peaks corresponding to dissolution during the anodic and cathodic scans. Several mechanisms of gold oxide formation and dissolution have been already thoroughly described, although the exact reaction pathway is still not clarified.7,55
As already observed for polycrystalline material, the Pd dissolution per cycle (≈117 ng cm−2) is more extensive than those of gold and other noble metals.56,65 Moreover, instead of two separate peaks resulting from oxidation and reduction, the presence of a third and sometimes fourth peak indicates that additional processes, recently clarified,56 play an important role. These can be related to the complex structure of Pd oxides, the oxidation state of Pd and the chemical composition of the oxide. Contradicting reports suggest, on the basis of CV measurements, that the formation of the first monolayer of Pd(II)-oxide occurs either in the 1.45–1.50 VRHE potential range or between 1.1–1.3 VRHE.61 At higher anodic potentials (>1.4 VRHE), a further oxidation occurs on the surface leading to the formation of Pd(IV)-oxide.61,66 Our experimental results confirm a change in the oxide composition due to the reduction of surface Pds(IV)-oxide to Pd(II)-oxide and Pd-metal followed by transient dissolution (first cathodic peak in Fig. 2), which occurs at 1.1–1.2 VRHE. The second cathodic peak corresponds to the reduction of the remaining bulk Pdb(IV) oxide layer in a non-reversible process which occurs in parallel with Pd(II)-oxide reduction to Pd-metal and dissolution of Pd-metal.56
Concerning the behavior of the alloyed metals, controversial results regarding increased stability of metals in alloyed nanoparticles compared to the pure metals are reported.67–71 In fact, some theoretical DFT calculations claim that the presence of an alloying element would induce a shift in the oxidation and dissolution potential, thus leading to stabilization of the alloy. This is possibly related to delayed coverage of O* and OH* intermediates. Often, the doping of Au is reported to have a positive effect on the stabilization of other noble metals such as Pt.72 Recently, however, Cherevko et al. showed that a Pt sub-monolayer on bulk Au is not stable, but rather shows significant dissolution of both Au and Pt similar to the pure polycrystalline elements.73 In our case, the Au and Pd dissolved masses in the alloy normalized by the nanoparticle total surface area (insets in Fig. 2A and B) are in absolute terms approximately half of those for the pure metals (for Pd ≈ 60%, for Au ≈ 50%). Considering that the nominal stoichiometry is 50% Au and 50% Pd, and assuming that the initial surface composition does not differ significantly, this suggests that the dissolution normalized by the respective nanoparticle surface area in the alloyed nanoparticles is approximately in line with that of the pure metals. Nevertheless, a possible non-homogeneity of the alloys and the difficulty in estimating the real surface composition make the interpretation of the results rather challenging. A study on a model surface would be therefore recommended to confirm/exclude the effect of gold on the overall dissolution per cycle.
Interestingly, however, the dissolution onset potential of Pd in the alloyed catalyst (see Fig. S3.2 in the ESI†) is slightly higher (approximately 30 mV higher, around 0.81 VRHE) compared to that of pure Pd. Similarly, Cherevko et al. showed that the onset of Pt dissolution after intermixing shift to slightly higher potential than those of the pure elements.73 Furthermore, in line with the oxide reduction peak shift (Fig. 1), the cathodic Pd dissolution of the alloyed material ends significantly earlier, one more time confirming a correlation between Pd-oxide reduction and cathodic dissolution processes. Therefore, alloying clearly influences the dissolution onset and final potentials, whereas no significant effect on the quantitative dissolution is observed.
Changing the upper potential limit (UPL) or the scan rate has no significant influence on the dissolution onset potentials. Nevertheless, as shown for polycrystalline metals, the rate of dissolution and the shape of the dissolution peaks and profiles for the AuPd alloy are strictly related to the UPL (see Fig. S4 in the ESI†) and scan rate. At higher scan rates, it is for example not possible to distinguish the two cathodic peaks even at higher UPL, as can be seen already from the cycles at 10 mV s−1 in Fig. 3. The overlap between dissolution peaks at higher scan rates was previously observed for polycrystalline Pt and related to the technical limitations of the setup.74
In conclusion, considering the dissolution onset potentials, it is possible to define a stability window for bimetallic nanoparticles like the AuPd catalyst: below the Pd dissolution onset potential (≈0.8 VRHE), virtually no metal is leached out from the catalyst surface, so that the composition remains unchanged. Above 0.8 VRHE, severe dissolution of Pd and Au (above 1.3 VRHE) occurs, which leads to changes in surface composition and long-term degradation of the catalyst. These considerations of course do not take into account surface restructuring and metal migration, which might occur at low potentials.
3.2 Influence of the acidic medium in dealloying
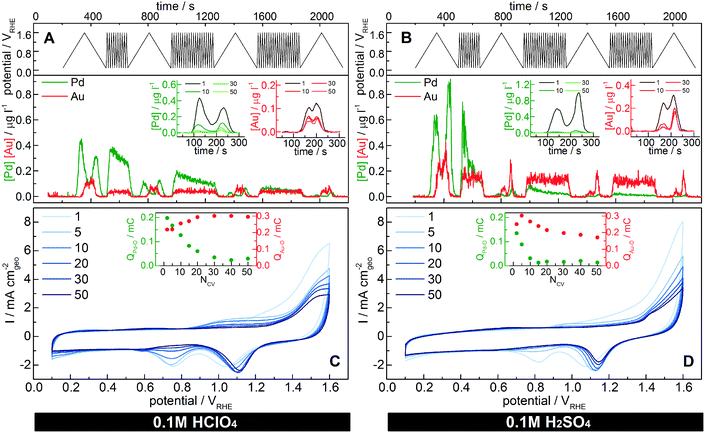
Online dissolution and voltammetric profiles [0.1–1.6 VRHE] are recorded in Ar-purged 0.1 M HClO4 and H2SO4 (Fig. 3) to characterize the changes in dissolution rate and surface composition of the particles over time. Such a high overpotential is chosen in order to (I) accelerate the degradation and (II) monitor the gold reduction peak that is visible only with scans to high potentials. In Fig. 3, the dissolution is not normalized to the surface area, since the total area and the surface composition change during the measurement due to dissolution and dealloying. For the sake of comparison, the same measurement has been performed also with the pure metal counterparts (see Fig. S5.3 in the ESI†). The charges associated with the two characteristic reduction peaks in the profile are proportional to the Au and Pd surface areas, respectively. However, as previously discussed, the extrapolation of surface area in alloys is ambiguous, therefore we simply report the associated reduction charges (insets in Fig. 3C and D), which in any case are intended to be proportional to the Pd and Au surface areas.50 cycle profiles (1, 5, 10, 20, 30 and 50) with a scan rate of 200 mV s−1 are shown in Fig. 3C and D. The surface and its composition change rapidly as confirmed by the reduction charges: the Pd-oxide reduction peak decreases, while that of the Au-oxide increases in magnitude during the first cycles. At the same time, the amount of dissolved Pd constantly drops as a consequence of the decrease in surface Pd. As described in earlier reports,39,60,62,75,76 the voltammograms of the Au–Pd alloys show a significant shift during continuous potential cycling in acidic media to sufficiently high potentials. In the literature, this was attributed to (I) Au migration to the surface,39 (II) potential-dependent Pd surface segregation18 or (III) selective Pd removal.62 Our results show that the main reason for surface Au enrichment is dealloying/dissolution. Of course, the other two, especially surface diffusion of gold atoms,77 cannot be completely excluded, however their role in this process is considered minor compared to dissolution. Indeed, Pd dissolves at a much higher rate than Au during the first cycles; thus, Au is increasingly exposed to the surface, hence forming a gold “skin” (Fig. 4). While this might be positive for materials like Pt based alloys (PtM) used for ORR leading to an enhanced Pt surface area, in applications where the surface metal composition is crucial for activity and selectivity, dealloying needs to be avoided to retain the desired initial properties. Detailed information about these applications is therefore required and needs to be compared to the bimetallic stability window. Nevertheless, dealloying can cause the formation of a porous bimetallic structure (as shown for the dealloyed PtNi nanocatalyst78) that can lead to a new interesting perspective as shown for the gold nanoporous catalyst.79–81
Interestingly, the palladium dissolution throughout the measurement does not simply decrease quantitatively, but also the profile changes as shown in the comparison of the cycles with slower scan rates (insets in Fig. 3A and B). Indeed, the anodic dissolution onset potential shifts positively from 0.9 VRHE of the first cycle to approximately 1.0 VRHE. A similar positive shift was observed for the sub-monolayer of Pt@Au dissolution.73 During the cathodic scan, the dissolution maxima (only one peak is distinguishable at this scan rate) as well as the dissolution final potential slightly shift to higher potentials. This is correlated to the decrease in Pd content with dissolution, which produces a more “intimate” mixed alloy with finely dispersed palladium in the gold matrix. Indeed, the Pd–O reduction peak potential in AuPd alloys is strictly correlated to the Pd content (Fig. 1): the less palladium that is present in the alloy, the higher the potential for Pd–O reduction,17 which explains the change in dissolution maximum potentials.
The catalyst dissolution behavior is here studied also in a different acidic medium (sulfuric acid). The dissolution onset potential for alloyed Au (see Fig. S5.2 in the ESI†) is shifted by approximately 50 mV (≈1.25 VRHE in sulfuric acid and ≈1.3 VRHE in perchloric acid). This change is in accordance with measurements on polycrystalline gold electrodes,7 where a shift of about 100 mV was observed (≈1.3 VRHE in sulfuric acid and ≈1.4 VRHE in perchloric acid). On the other hand, the alloyed Pd behaves more like Pt: its dissolution onset potential does not change, in accordance with other studies on polycrystalline Pt.7 Instead, the amount of dissolved palladium per cycle changes significantly with the acid. Indeed, during the first cycle, Pd is dissolved more in sulfuric acid (≈0.24 ng) compared to perchloric acid (≈0.13 ng). This difference in Pd removal is mirrored in the recorded CVs (Fig. 3C and D) by a faster decrease of the Pd-oxide reduction peak intensity:39 in H2SO4, Pd disappears after 10 CV cycles, whereas in HClO4, it is still detectable after 50 CV cycles. Therefore, the enhanced electrodissolution of Pd depends on the nature of anions present in the electrolyte, as they facilitate the formation of products and/or intermediates.56,61 In particular, based on the results reported in the literature, sulfuric acid promotes Pd electrodissolution more than perchloric acid.56
In both cases, the last CVs (Fig. 3C and D after 50 cycles) indicate the presence of a gold-enriched catalyst with probably a core–shell configuration, even though some isolated Pd atoms might still be present on the catalyst surface. Indeed, ICP-MS measurements of the degraded catalyst show a final Pd/Au ratio of 30/70 mol% after 50 CV cycles to 1.6 VRHE in perchloric acid, thus confirming the presence of Pd in the core even after the degradation measurement.
3.3 Influence of gas
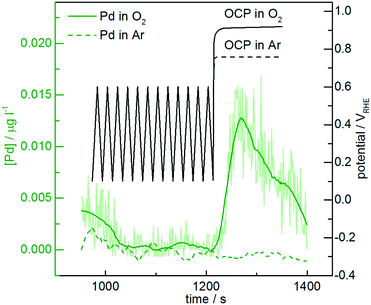
Online dissolution of AuPd nanoparticles is recorded in O2-purged 0.1 M HClO4 (Fig. 5). While no significant differences with the Ar-purged electrolyte are observed during potential cycling below the dissolution onset, the presence of oxygen leads to a shift in the open circuit potential (OCP). Namely, the OCP in the oxygen-purged electrolyte reaches approximately 0.9 VRHE, slightly above the measured dissolution onset potential, while in the argon-purged electrolyte it remains below 0.8 VRHE. Therefore, Pd is dissolved at the OCP in the presence of oxygen. Gas-induced changes in alloy surface composition have already been reported in the heterogeneous catalysis literature,39,82 which are commonly attributed to metal migration. According to our results, however, we suggest that selective dissolution in the presence of different gases also plays an important role in determining the surface composition. This is particularly relevant for the long-term stability of bimetallic nanoparticles in reactions that require gases such as O2, CO and O3 which can cause high OCP values, or in reactors that are shut down frequently and air is able to diffuse in. Therefore, gas-induced dealloying/dissolution has also to be taken into consideration in heterogeneous catalysis, where no potential control is applied.4 Conclusions
In summary, in this work we showed an extensive dissolution study on alloyed AuPd nanoparticles supported directly on an electrode. Using a unique technique that combines electrochemical measurements with online mass spectroscopy, we showed how the reaction environment strongly influences metal dissolution and dealloying. In particular, different electrolytes cause a significant variation in the dissolution rate depending on the nature of anions and/or cations present in the solution, and dissolved oxygen gas plays a key role in enhancing the dissolution rates by shifting the open circuit potential.Even though the interpretation of the results is challenging due to the difficulty in estimation of the precise surface composition in the alloyed catalyst, the quantitative normalized dissolution indicates that the dissolution of Au and Pd in the alloy is approximately half of the normalized dissolution of the metal counterparts. Considering the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 molar ratio of the synthesized alloy, no major stabilization of Pd was therefore observed. On the other hand, the measured Pd dissolution profiles are different for alloyed Pd compared to the pure metal: the anodic onset and cathodic final dissolution potentials are shifted.
1 molar ratio of the synthesized alloy, no major stabilization of Pd was therefore observed. On the other hand, the measured Pd dissolution profiles are different for alloyed Pd compared to the pure metal: the anodic onset and cathodic final dissolution potentials are shifted.
A well-defined stability window can be deduced from the presented results below ≈0.8 VRHE and in the presence of a gas that causes low OCP, where no dissolution/dealloying of Pd occurs. In such cases, changes in surface composition are only assignable to metal migration or segregation, which were not addressed here. In contrast with other work in the literature, we have shown that the main contribution to changes in surface composition comes from selective dissolution rather than metal migration above potentials of 0.8 VRHE. The faster dissolution rate of palladium compared to gold induces a gold surface enrichment. Indeed, the palladium dissolution decreases to almost zero and its profile continuously changes throughout the degradation.
The AuPd catalyst was used here as a model system for dissolution and selective dealloying. However, the results and implications can be extended to any bimetallic system. With this study, it was shown that the catalyst structure, surface composition, and thus activity can change over time under reaction environments and conditions due to selective dissolution. In turn, dealloying could be also exploited positively with selective dissolution by subjecting particles to electrochemical conditions, in order to control and tune the catalyst surface composition. With this “activation”, the bimetallic effects could be optimized to achieve and maintain enhanced catalytic activity.
Our results imply that by defining the experimental conditions and thus influencing the dissolution, it might be possible to control the surface composition precisely. On the other hand, in real applications, where a determined surface composition is required to achieve an optimum in activity and selectivity, it is difficult to avoid dissolution and thus to control the bimetallic surface composition over long reaction times. In fact, in fuel cells, it is likely to have potential spikes which exceed the stability window during start and stop conditions, while in heterogeneous catalysis, mixtures of gases might lead to dealloying through changes in the potential of the system. In both cases, this is detrimental for application based on reactions, where the coexistence of both metals on the surface is necessary (i.e. peroxide synthesis, alcohol oxidation, formic acid oxidation).
In conclusion, having exhaustive dissolution/dealloying data combined with precise information about the reaction environment is of crucial importance to guarantee the performance and stability of all materials that rely on ensemble effects. Indeed, if potential fluctuations occur, the resulting dealloying can dramatically change in a short time their surface composition and therefore their activity.
Acknowledgements
E. P. acknowledges financial support from the IMPRS-SurMat doctoral program. We thank The MAXNET Energy for financial support. S. G. acknowledges financial support from BASF. Open Access funding provided by the Max Planck Society.References
- S. J. Freakley, Q. He, C. J. Kiely and G. J. Hutchings, Catal. Lett., 2015, 145, 71–79 CrossRef CAS.
- M. Haruta, T. Kobayashi, H. Sano and N. Yamada, Chem. Lett., 1987, 405–408, DOI:10.1246/Cl.1987.405.
- A. S. K. Hashmi, Chem. Rev., 2007, 107, 3180–3211 CrossRef CAS PubMed.
- A. S. K. Hashmi, Angew. Chem., Int. Ed., 2010, 49, 5232–5241 CrossRef CAS PubMed.
- A. S. K. Hashmi and G. J. Hutchings, Angew. Chem., Int. Ed., 2006, 45, 7896–7936 CrossRef PubMed.
- P. Rodriguez and M. T. M. Koper, Phys. Chem. Chem. Phys., 2014, 16, 13583–13594 RSC.
- S. Cherevko, A. R. Zeradjanin, G. P. Keeley and K. J. J. Mayrhofer, J. Electrochem. Soc., 2014, 161, H822–H830 CrossRef.
- A. S. K. Hashmi, C. Lothschutz, R. Dopp, M. Ackermann, J. D. Becker, M. Rudolph, C. Scholz and F. Rominger, Adv. Synth. Catal., 2012, 354, 133–147 CrossRef CAS.
- D. I. Enache, J. K. Edwards, P. Landon, B. Solsona-Espriu, A. F. Carley, A. A. Herzing, M. Watanabe, C. J. Kiely, D. W. Knight and G. J. Hutchings, Science, 2006, 311, 362–365 CrossRef CAS PubMed.
- J. K. Edwards, B. Solsona, E. Ntainjua N, A. F. Carley, A. A. Herzing, C. J. Kiely and G. J. Hutchings, Science, 2009, 323, 1037–1041 CrossRef CAS PubMed.
- L. Kesavan, R. Tiruvalam, M. H. Ab Rahim, M. I. bin Saiman, D. I. Enache, R. L. Jenkins, N. Dimitratos, J. A. Lopez-Sanchez, S. H. Taylor, D. W. Knight, C. J. Kiely and G. J. Hutchings, Science, 2011, 331, 195–199 CrossRef CAS PubMed.
- M. H. Ab Rahim, M. M. Forde, R. L. Jenkins, C. Hammond, Q. He, N. Dimitratos, J. A. Lopez-Sanchez, A. F. Carley, S. H. Taylor, D. J. Willock, D. M. Murphy, C. J. Kiely and G. J. Hutchings, Angew. Chem., Int. Ed., 2013, 52, 1280–1284 CrossRef CAS PubMed.
- S. T. Bliznakov, M. B. Vukmirovic, L. Yang, E. A. Sutter and R. R. Adzic, J. Electrochem. Soc., 2012, 159, F501–F506 CrossRef CAS.
- J. L. Fernandez, V. Raghuveer, A. Manthiram and A. J. Bard, J. Am. Chem. Soc., 2005, 127, 13100–13101 CrossRef CAS PubMed.
- K. A. Kuttiyiel, K. Sasaki, D. Su, L. J. Wu, Y. M. Zhu and R. R. Adzic, Nat. Commun., 2014, 5, 5185 CrossRef CAS PubMed.
- Y. C. Xing, Y. Cai, M. B. Vukmirovic, W. P. Zhou, H. Karan, J. X. Wang and R. R. Adzic, J. Phys. Chem. Lett., 2010, 1, 3238–3242 CrossRef CAS.
- J. S. Jirkovsky, I. Panas, E. Ahlberg, M. Halasa, S. Romani and D. J. Schiffrin, J. Am. Chem. Soc., 2011, 133, 19432–19441 CrossRef CAS PubMed.
- J. S. Jirkovsky, I. Panas, S. Romani, E. Ahlberg and D. J. Schiffrin, J. Phys. Chem. Lett., 2012, 3, 315–321 CrossRef CAS.
- F. Yang, K. Cheng, T. H. Wu, Y. Zhang, J. L. Yin, G. L. Wang and D. X. Cao, J. Power Sources, 2013, 233, 252–258 CrossRef CAS.
- M. Nie, H. L. Tang, Z. D. Wei, S. P. Jiang and P. K. Shen, Electrochem. Commun., 2007, 9, 2375–2379 CrossRef CAS.
- Y. W. Lee, M. Kim, Y. Kim, S. W. Kang, J. H. Lee and S. W. Han, J. Phys. Chem. C, 2010, 114, 7689–7693 CAS.
- C. H. Cui, J. W. Yu, H. H. Li, M. R. Gao, H. W. Liang and S. H. Yu, ACS Nano, 2011, 5, 4211–4218 CrossRef CAS PubMed.
- X. Y. Lang, H. Guo, L. Y. Chen, A. Kudo, J. S. Yu, W. Zhang, A. Inoue and M. W. Chen, J. Phys. Chem. C, 2010, 114, 2600–2603 CAS.
- A. S. K. Hashmi, R. Döpp, C. Lothschütz, M. Rudolph, D. Riedel and F. Rominger, Adv. Synth. Catal., 2010, 352, 1307–1314 CrossRef CAS.
- A. S. K. Hashmi, M. Ghanbari, M. Rudolph and F. Rominger, Chem. – Eur. J., 2012, 18, 8113–8119 CrossRef CAS PubMed.
- A. S. K. Hashmi, C. Lothschütz, R. Döpp, M. Rudolph, T. D. Ramamurthi and F. Rominger, Angew. Chem., Int. Ed., 2009, 48, 8243–8246 CrossRef CAS PubMed.
- M. M. Hansmann, M. Pernpointner, R. Döpp and A. S. K. Hashmi, Chem. – Eur. J., 2013, 19, 15290–15303 CrossRef CAS PubMed.
- J. R. Kitchin, J. K. Norskov, M. A. Barteau and J. G. Chen, Phys. Rev. Lett., 2004, 93, 156801 CrossRef CAS PubMed.
- J. A. Rodriguez and D. W. Goodman, Science, 1992, 257, 897–903 CAS.
- V. Stamenkovic, B. S. Mun, K. J. J. Mayrhofer, P. N. Ross, N. M. Markovic, J. Rossmeisl, J. Greeley and J. K. Norskov, Angew. Chem., Int. Ed., 2006, 45, 2897–2901 CrossRef CAS PubMed.
- M. Mavrikakis, B. Hammer and J. K. Norskov, Phys. Rev. Lett., 1998, 81, 2819–2822 CrossRef.
- L. A. Kibler, A. M. El-Aziz, R. Hoyer and D. M. Kolb, Angew. Chem., Int. Ed., 2005, 44, 2080–2084 CrossRef CAS PubMed.
- M. S. Chen, D. Kumar, C. W. Yi and D. W. Goodman, Science, 2005, 310, 291–293 CrossRef CAS PubMed.
- F. Maroun, F. Ozanam, O. M. Magnussen and R. J. Behm, Science, 2001, 293, 1811–1814 CrossRef CAS PubMed.
- J. Pritchard, L. Kesavan, M. Piccinini, Q. He, R. Tiruvalam, N. Dimitratos, J. A. Lopez-Sanchez, A. F. Carley, J. K. Edwards, C. J. Kiely and G. J. Hutchings, Langmuir, 2010, 26, 16568–16577 CrossRef CAS PubMed.
- S. Siahrostami, A. Verdaguer-Casadevall, M. Karamad, D. Deiana, P. Malacrida, B. Wickman, M. Escudero-Escribano, E. A. Paoli, R. Frydendal, T. W. Hansen, I. Chorkendorff, I. E. L. Stephens and J. Rossmeisl, Nat. Mater., 2013, 12, 1137–1143 CrossRef CAS PubMed.
- A. Verdaguer-Casadevall, D. Deiana, M. Karamad, S. Siahrostami, P. Malacrida, T. W. Hansen, J. Rossmeisl, I. Chorkendorff and I. E. L. Stephens, Nano Lett., 2014, 14, 1603–1608 CrossRef CAS PubMed.
- P. Liu and J. K. Norskov, Phys. Chem. Chem. Phys., 2001, 3, 3814–3818 RSC.
- C. N. Brodsky, A. P. Young, K. C. Ng, C. H. Kuo and C. K. Tsung, ACS Nano, 2014, 8, 9368–9378 CrossRef CAS PubMed.
- S. Suzuki, T. Onodera, J. Kawaji, T. Mizukami, Y. Takamori, H. Daimon and M. Morishima, ECS Trans., 2010, 33, 321–332 CAS.
- T. Ghosh, B. M. Leonard, Q. Zhou and F. J. DiSalvo, Chem. Mater., 2010, 22, 2190–2202 CrossRef CAS.
- B. M. Leonard, Q. Zhou, D. N. Wu and F. J. DiSalvo, Chem. Mater., 2011, 23, 1136–1146 CrossRef CAS.
- V. R. Stamenkovic, B. S. Mun, K. J. J. Mayrhofer, P. N. Ross and N. M. Markovic, J. Am. Chem. Soc., 2006, 128, 8813–8819 CrossRef CAS PubMed.
- J. W. Hong, D. Kim, Y. W. Lee, M. Kim, S. W. Kang and S. W. Han, Angew. Chem., Int. Ed., 2011, 50, 8876–8880 CrossRef CAS PubMed.
- I. W. C. E. Arends and R. A. Sheldon, Appl. Catal., A, 2001, 212, 175–187 CrossRef CAS.
- R. Borup, J. Meyers, B. Pivovar, Y. S. Kim, R. Mukundan, N. Garland, D. Myers, M. Wilson, F. Garzon, D. Wood, P. Zelenay, K. More, K. Stroh, T. Zawodzinski, J. Boncella, J. E. McGrath, M. Inaba, K. Miyatake, M. Hori, K. Ota, Z. Ogumi, S. Miyata, A. Nishikata, Z. Siroma, Y. Uchimoto, K. Yasuda, K. I. Kimijima and N. Iwashita, Chem. Rev., 2007, 107, 3904–3951 CrossRef CAS PubMed.
- F. Tao, M. E. Grass, Y. W. Zhang, D. R. Butcher, F. Aksoy, S. Aloni, V. Altoe, S. Alayoglu, J. R. Renzas, C. K. Tsung, Z. W. Zhu, Z. Liu, M. Salmeron and G. A. Somorjai, J. Am. Chem. Soc., 2010, 132, 8697–8703 CrossRef CAS PubMed.
- S. Mezzavilla, C. Baldizzone, A.-C. Swertz, N. Hodnik, E. Pizzutilo, G. Polymeros, G. P. Keeley, J. Knossalla, M. Heggen, K. J. J. Mayrhofer and F. Schüth, ACS Catal., 2016, 6, 8058–8068 CrossRef CAS.
- S. Koh and P. Strasser, J. Am. Chem. Soc., 2007, 129, 12624–12625 CrossRef CAS PubMed.
- S. Rudi, L. Gan, C. H. Cui, M. Gliech and P. Strasser, J. Electrochem. Soc., 2015, 162, F403–F409 CrossRef CAS.
- U. DoE, Hydrogen, Fuel Cells and Infrastructure Technologies Program: Multiyear Research, Development and Demonstration Plan, 2011 Search PubMed.
- S. O. Klemm, A. A. Topalov, C. A. Laska and K. J. J. Mayrhofer, Electrochem. Commun., 2011, 13, 1533–1535 CrossRef CAS.
- S. Mezzavilla, S. Cherevko, C. Baldizzone, E. Pizzutilo, G. Polymeros and K. J. J. Mayrhofer, ChemElectroChem, 2016, 3, 1524–1536 CrossRef CAS.
- S. Cherevko, A. R. Zeradjanin, A. A. Topalov, N. Kulyk, I. Katsounaros and K. J. J. Mayrhofer, ChemCatChem, 2014, 6, 2219–2223 CrossRef CAS.
- S. Cherevko, A. A. Topalov, A. R. Zeradjanin, I. Katsounaros and K. J. J. Mayrhofer, RSC Adv., 2013, 3, 16516–16527 RSC.
- E. Pizzutilo, S. Geiger, S. J. Freakley, A. Mingers, S. Cherevko, G. J. Hutchings and K. J. J. Mayrhofer, Electrochim. Acta, 2017, 229, 467–477 CrossRef CAS.
- E. Pizzutilo, S. Geiger, J.-P. Grote, A. Mingers, K. J. J. Mayrhofer, M. Arenz and S. Cherevko, J. Electrochem. Soc., 2016, 163, F1510–F1514 CrossRef CAS.
- A. Pareek, G. N. Ankah, S. Cherevko, P. Ebbinghaus, K. J. J. Mayrhofer, A. Erbe and F. U. Renner, RSC Adv., 2013, 3, 6586–6595 RSC.
- P. Jovanovic, A. Pavlisic, V. S. Selih, M. Sala, N. Hodnik, M. Bele, S. Hocevar and M. Gaberscek, ChemCatChem, 2014, 6, 449–453 CrossRef CAS.
- H. Erikson, A. Sarapuu, J. Kozlova, L. Matisen, V. Sammelselg and K. Tammeveski, Electrocatalysis, 2015, 6, 77–85 CrossRef CAS.
- M. Grdeń, M. Łukaszewski, G. Jerkiewicz and A. Czerwiński, Electrochim. Acta, 2008, 53, 7583–7598 CrossRef.
- M. Lukaszewski and A. Czerwinski, Electrochim. Acta, 2003, 48, 2435–2445 CrossRef CAS.
- S. Henning, J. Herranz and H. A. Gasteiger, J. Electrochem. Soc., 2015, 162, F178–F189 CrossRef CAS.
- G. P. Keeley, S. Cherevko and K. J. Mayrhofer, ChemElectroChem, 2016, 3, 51–54 CrossRef CAS PubMed.
- D. A. J. Rand and R. Woods, J. Electroanal. Chem., 1972, 35, 209–218 CrossRef CAS.
- A. N. Correia, L. H. Mascaro, S. A. S. Machado and L. A. Avaca, Electrochim. Acta, 1997, 42, 493–495 CrossRef CAS.
- V. R. Stamenkovic, B. S. Mun, M. Arenz, K. J. J. Mayrhofer, C. A. Lucas, G. F. Wang, P. N. Ross and N. M. Markovic, Nat. Mater., 2007, 6, 241–247 CrossRef CAS PubMed.
- G. E. Ramirez-Caballero, Y. G. Ma, R. Callejas-Tovar and P. B. Balbuena, Phys. Chem. Chem. Phys., 2010, 12, 2209–2218 RSC.
- K. Sasaki, H. Naohara, Y. Cai, Y. M. Choi, P. Liu, M. B. Vukmirovic, J. X. Wang and R. R. Adzic, Angew. Chem., Int. Ed., 2010, 49, 8602–8607 CrossRef CAS PubMed.
- K. Sasaki, H. Naohara, Y. M. Choi, Y. Cai, W. F. Chen, P. Liu and R. R. Adzic, Nat. Commun., 2012, 3, 1115 CrossRef PubMed.
- J. Greeley and J. K. Norskov, Electrochim. Acta, 2007, 52, 5829–5836 CrossRef CAS.
- M. Gatalo, P. Jovanovič, G. Polymeros, J.-P. Grote, A. Pavlišič, F. Ruiz-Zepeda, V. S. Šelih, M. Šala, S. Hočevar, M. Bele, K. J. J. Mayrhofer, N. Hodnik and M. Gaberšček, ACS Catal., 2016, 6, 1630–1634 CrossRef CAS.
- S. Cherevko, G. P. Keeley, N. Kulyk and K. J. J. Mayrhofer, J. Electrochem. Soc., 2016, 163, H228–H233 CrossRef CAS.
- A. A. Topalov, S. Cherevko, A. R. Zeradjanin, J. C. Meier, I. Katsounaros and K. J. J. Mayrhofer, Chem. Sci., 2014, 5, 631–638 RSC.
- D. A. J. Rand and R. Woods, J. Electroanal. Chem., 1972, 36, 57–69 CrossRef CAS.
- R. Woods, Electrochim. Acta, 1969, 14, 632–635 CrossRef CAS.
- J. M. Dona and J. Gonzalezvelasco, J. Phys. Chem., 1993, 97, 4714–4719 CrossRef CAS.
- C. Baldizzone, L. Gan, N. Hodnik, G. P. Keeley, A. Kostka, M. Heggen, P. Strasser and K. J. J. Mayrhofer, ACS Catal., 2015, 5, 5000–5007 CrossRef CAS.
- T. Fujita, P. Guan, K. McKenna, X. Lang, A. Hirata, L. Zhang, T. Tokunaga, S. Arai, Y. Yamamoto, N. Tanaka, Y. Ishikawa, N. Asao, Y. Yamamoto, J. Erlebacher and M. Chen, Nat. Mater., 2012, 11, 775–780 CrossRef CAS PubMed.
- N. Asao, Y. Ishikawa, N. Hatakeyama, Menggenbateer, Y. Yamamoto, M. Chen, W. Zhang and A. Inoue, Angew. Chem., Int. Ed., 2010, 49, 10093–10095 CrossRef CAS PubMed.
- J. Biener, M. M. Biener, R. J. Madix and C. M. Friend, ACS Catal., 2015, 5, 6263–6270 CrossRef CAS.
- S. Alayoglu, F. Tao, V. Altoe, C. Specht, Z. W. Zhu, F. Aksoy, D. R. Butcher, R. J. Renzas, Z. Liu and G. A. Somorjai, Catal. Lett., 2011, 141, 633–640 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c7cy00291b |
| This journal is © The Royal Society of Chemistry 2017 |