Theories and simulations of roaming
Abstract
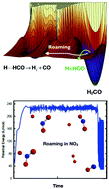
The phenomenon of roaming in chemical reactions has now become both commonly observed in experiment and extensively supported by theory and simulations. Roaming occurs in highly-excited molecules when the trajectories of atomic motion often bypass the minimum energy pathway and produce reaction in unexpected ways from unlikely geometries. The prototypical example is the unimolecular dissociation of formaldehyde (H2CO), in which the “normal” reaction proceeds through a tight transition state to yield H2 + CO but for which a high fraction of dissociations take place via a “roaming” mechanism in which one H atom moves far from the HCO, almost to dissociation, and then returns to abstract the second H atom. We review below the theories and simulations that have recently been developed to address and understand this new reaction phenomenon.
- This article is part of the themed collection: Chemical reaction dynamics


 Please wait while we load your content...
Please wait while we load your content...