Two-dimensional boron: structures, properties and applications
Abstract
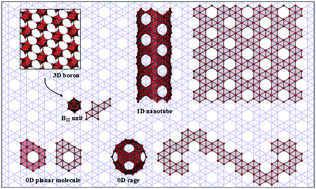
Situated between metals and non-metals in the periodic table, boron is one of the most chemically versatile elements, forming at least sixteen bulk polymorphs composed of interlinked boron polyhedra. In low-dimensionality, boron chemistry remains or becomes even more intriguing since boron clusters with several to tens of atoms favor planar or cage-like structures, which are similar to their carbon counterparts in terms of conformation and electronic structure. The similarity between boron and carbon has raised a question of whether there exists stable two-dimensional (2D) boron, as a conceptual precursor, from which other boron nanostructures may be built. Here, we review the current theoretical and experimental progress in realizing boron atomic layers. Starting by describing a decade-long effort towards understanding the size-dependent structures of boron clusters, we present how theory plays a role in extrapolating boron clusters into 2D form, from a freestanding state to that on substrates, as well as in exploring practical routes for their synthesis that recently culminated in experimental realization. While 2D boron has been revealed to have unusual mechanical, electronic and chemical properties, materializing its potential in practical applications remains largely impeded by lack of routes towards transfer from substrates and controlled synthesis of quality samples.


 Please wait while we load your content...
Please wait while we load your content...