Theory of 2D crystals: graphene and beyond
Abstract
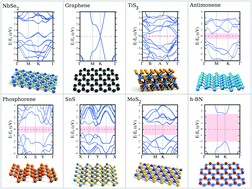
This tutorial review presents an overview of the basic theoretical aspects of two-dimensional (2D) crystals. We revise essential aspects of graphene and the new families of semiconducting 2D materials, like transition metal dichalcogenides or black phosphorus. Minimal theoretical models for various materials are presented. Some of the exciting new possibilities offered by 2D crystals are discussed, such as manipulation and control of quantum degrees of freedom (spin and pseudospin), confinement of excitons, control of the electronic and optical properties with strain engineering, or unconventional superconducting phases.
- This article is part of the themed collections: Graphene Chemistry and Primer


 Please wait while we load your content...
Please wait while we load your content...