State-to-state mode specificity in H + DOH(ν_OH = 1) → HD + OH(ν₂ = 0) reaction: vibrational non-adiabaticity or local-mode excitation?

Abstract

It is well established that chemical reactions often involve only a small number of atoms near the reaction site, and the remainder of the reactant molecules are mostly spectators. It is thus of great importance to understand the role played by the active as well as spectator modes in chemical dynamics. In this work, we examine in great detail the influence of reactant modes on the reactivity and product state distribution, using a four-atom prototypical reaction as the example. State-of-the-art full-dimensional state-to-state quantum dynamics reveal a startling observation in which the DOH(ν_OH = 1) molecule reacts with a H atom to produce a vibrationless OH product. This is surprising because OH is considered as a spectator in this reaction and its internal energy should be sequestered throughout the reaction. By careful analysis within the local-mode regime, we demonstrate that the surprising reactivity is not due to vibrational non-adiabaticity during the reaction. Rather, it can be attributed to a small OD excited local-mode component in the reactant wavefunction. The quantum state-resolved dissection of this prototype reaction helps to advance our understanding of larger reactive systems.

---

Introduction

Recently, there has been increasing attention paid to quantum dynamical studies of bimolecular reactions beyond the atom–diatom paradigm that has dominated the field of reaction dynamics for a long time.^1–4 Reactions with polyatomic reactants are of course more challenging, but also provide a much wider spectrum of interesting phenomena, which have attracted strong experimental interest.^5–7 Taking the example of mode specificity, which is of great importance in reaction dynamics,⁸ a polyatomic molecule with 3N – 6 vibrational modes (N being the number of atoms in the molecule) presents a much richer variety of possibilities, especially when comparing with the single vibrational mode in a diatom. Quantum dynamical studies of such reactions at the state-to-state level is extremely challenging, but much progress has recently been made thanks to the availability of high-quality reactive potential energy surfaces (PESs)^9–11 and advances in quantum reactive scattering algorithms.¹²

Our ability to unravel the state-to-state quantum dynamics is not only important for specific prototypical systems, but may also lead to general principles that can be applied to larger systems that are not currently amenable to quantum treatments. It is well established that chemical reactions often occur locally, involving only a small number of active modes. The other modes do not participate chemically. It is thus vital to understand the roles of the active as well as spectator modes in chemical dynamics. In this work, we focus on an atom–triatom system, which is a representative of four-atom reactions.¹³ We examine by detailed analysis of the state-to-state quantum dynamics of this system the influence of various reactant modes on reactivity and product energy disposal.

The specific isotopologue of the hydrogen abstraction reaction of water by a hydrogen atom is given below:

H + DOH → HD + OH, (R1)

which competes with

H + DOH → H₂ + OD. (R1′)

Thanks to the importance in combustion, these and other isotopologues of the reaction and their reverse have been studied experimentally by several groups.^14–21 A few accurate versions of the PES for this reaction are available.^22–25 The reaction dynamics of the forward and reverse reactions has been investigated quantum mechanically in full dimensionality by many,^26–48 but only a few have reported state-to-state differential cross sections.^{20,21,49–53} Since the PES for the ground electronic state of this reaction is highly reliable, full-dimensional quantum dynamical calculations with exact kinetic energy operators should yield accurate predictions. Indeed, excellent agreement has recently been demonstrated between such calculations and experimental measurements,^20,21 underscoring the full trustworthiness and predictive power of converged theoretical results.

The mode specificity and bond selectivity of the reaction has also been thoroughly investigated,^{33,34,44,46,48,50,53} which highlights the dominant role played by the transition state.^54,55 It is now well established that the mode specificity can be readily understood in terms of the coupling of the reactant vibrational normal modes with the reaction coordinate at the transition state. This coupling can be readily mapped out by projecting the reactant normal mode vectors on to the reaction coordinate vector, as suggested by the Sudden Vector Projection (SVP) model.⁵⁶ Very recently, the local-mode nature of the reaction has been addressed in several full-dimensional quantum dynamical studies,^50,57 which elucidated the mode specificity in this reaction.

These theoretical studies have greatly advanced our understanding of this prototypical reactive system. It is now commonly accepted that the non-reacting OH mode serves as a spectator mode,^14,16,50 which is nearly orthogonal to the reaction coordinate at the transition state.⁵⁸ As a result, exciting this mode has almost no effect on the reactivity for (R1). (Note that DOH, with the excited OH mode, proceeds largely via (R1′), in which the OH mode is almost perfectly aligned with the corresponding reaction coordinate,⁵⁸ but that is not the focus of this work.) In addition, energy deposited in the reactant OH mode is expected to stay in the mode throughout the reaction (R1), resulting in vibrationally excited OH. However, as shown below based on state-of-the-art full-dimensional state-to-state quantum calculations, a small amount of the OH product produced from reaction between the OH excited DOH and H atom is found in its ground vibrational state, especially at low collision energies. This surprising result might have two possible explanations. One is vibrational non-adiabaticity, which helps to transfer energy in the excited OH mode to other modes during the reaction, giving rise to the OH(ν₂ = 0) product. An alternative, and correct reason as we demonstrate here, is that the “de-excitation” of OH is caused by a minor local-mode component of the excited OD mode in the initial reactant wavefunction, in which the OH local-mode is not excited. Indeed, the localization of the OH and OD vibrations in the excited vibrational eigenstates of the DOH molecule is not complete, which leads to the surprising reactivity. As a result, the mode mixing is already present in the initial state, rather than during the reaction. The results and analysis help to shed light on the behavior of spectator modes in polyatomic reactions.

Theory

Results presented here were obtained using a reactant-coordinate based (RCB) method for state-to-state quantum reactive scattering of four-atom systems. Since this method has been discussed extensively in a recent publication,⁵³ no detail is given here. Briefly, the initial wave packet is launched in the reactant asymptote and propagated in time using an exact kinetic energy operator in the A + BCD reactant Jacobi coordinates, and the S-matrix elements were computed in the product channel via a series of transformations of the six-dimensional time-dependent wave packet. Some calculations were also performed with the potential averaged five-dimensional (PA5D) approximation with the non-reacting OH bond excluded from the dynamical calculations.²⁶ All partial waves were included. The neural network potential energy surface (PES) of the H₃O system developed by Chen et al.²⁵ was used. Parameters of the calculation are listed in Table S-I in the ESI.†

Results

A. Vibrational mode specificity in total reactivity

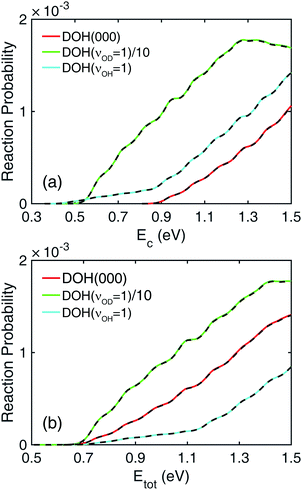
In Fig. 1, total reaction probabilities (J_tot = 0) of the H + DOH → HD + OH reaction are shown with the DOH reactant in three different vibrational states, labeled by (ν_OD, ν_b, ν_OH), which denote the quantum numbers of the OD stretching, bending, and OH stretching modes, respectively. To make different vibrational states of the DOH reactant more explicit, the (100) and (001) states are denoted below as DOH(ν_OD = 1) and DOH(ν_OH = 1), respectively. In panel (a), the reaction probabilities are plotted with respect to collision energy. The reaction probability from DOH(ν_OD = 1) is much larger than the ones from the other two modes by a factor of more than 20. This indicates that the energy deposited in the OD stretching mode is facilely utilized to promote the reaction, which is consistent with the active nature of this mode predicted by the SVP model.⁵⁸ On the other hand, it is quite interesting to note the unexpected behavior of the reaction probability from DOH(ν_OH = 1). If the OH bond can truly be considered as a spectator, the total reaction probability from DOH(ν_OH = 1) should be similar to the one from DOH(000) as the reactivity should not be affected by the vibrational excitation of the non-reacting OH bond. Surprisingly, the total reaction probability from DOH(ν_OH = 1) is substantially higher than the DOH(000) one and has a lower energy threshold. This behavior was also seen in recent work of Fu and Zhang on the same PES,⁴⁶ but without an explanation. Specifically, the reaction threshold is lowered to about 0.45 eV, which corresponds to the excitation energy of the DOH(ν_OH = 1) mode. It thus appears that the energy in the excited OH mode can somehow be used to promote the reaction, despite the fact that it is a spectator. Another distinct feature, regarding the energy dependence of the reaction probability from DOH(ν_OH = 1), are the apparently two different slopes in the probability with a kink near the threshold energy of the DOH(000) state at around 0.85 eV, as if there are more than one channels that contribute.

Fig. 1 Total reaction probabilities (J_tot = 0) of the H + DOH → HD + OH reaction with DOH reactant in three vibrational states, DOH(000), DOH(ν_OD = 1), and DOH(ν_OH = 1), respectively. The reaction probabilities are plotted with respect to collision energy in (a) and total energy in (b). Energy zero is set to the classical minimum energy at the H + DOH asymptote. Reaction probabilities obtained by sum of state-to-state reaction probabilities (black dashed lines) are compared with the ones calculated with flux operator (colored solid lines).

Before going to the analysis at the state-to-state level, it is worthwhile to plot the same total reaction probabilities with respect to total energy, namely the sum of collision and internal energies. Shown in panel (b) of Fig. 1 where the energy zero is set at the classical minimum energy in the H + DOH asymptote, it is interesting to note the reaction probabilities of the three modes all have roughly the same threshold in total energy, implying the comparable ability of translational energy and stretching vibration in initiating the reaction. It should be noted here that the DOH(ν_OH = 1) level has roughly 0.1 eV higher internal energy than the DOH(ν_OD = 1) level. To have the same threshold in total energy as for the DOH(ν_OH = 1) level, an extra of 0.1 eV translational energy is required for the DOH(ν_OD = 1) level.

B. Vibrational mode specificity in product state distributions

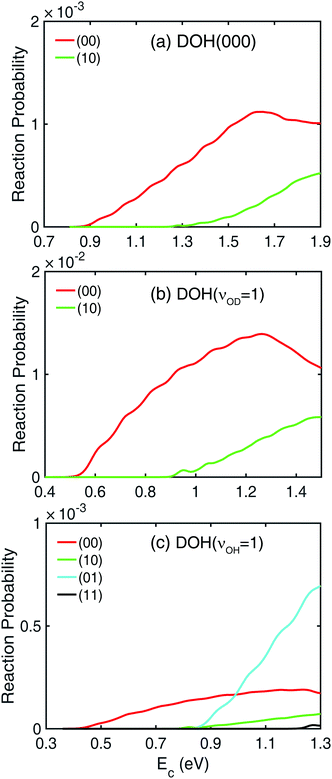
In Fig. 1, J_tot = 0 reaction probabilities obtained by sum of state-to-state reaction probabilities (black dashed lines) and the ones calculated with a flux operator (colored solid lines) agree pretty well with each other, which indicates the convergence of the state-to-state reaction probabilities. The final product vibrational state-revolved state-to-state reaction probabilities can be used to decompose the total reaction probabilities into contributions from different vibrational states of the HD and OH products, as shown in Fig. 2 for the three modes of the DOH reactant. In panel (a) for reaction from DOH(000), both the (00) and (10) product vibrational states are present. Here, the two numbers in the bracket (ν₁, ν₂) denote the vibrational quantum numbers of the HD and OH products, respectively. Near the threshold energy of 0.85 eV, the HD and OH products are both in their vibrational ground states. When the collision energy increases by 0.45 eV above the threshold, the (10) product channel starts to appear due to the available energy to access the vibrationally excited HD state. This vibrationally excited HD product can be rationalized by the large coupling of the HD vibration to the reaction coordinate at the transition-state.⁵⁸ Similarly for DOH(ν_OD = 1) in panel (b), the same two branches are present but with a lower threshold energy. However, no noticeable (01) state population is observed from the two initial states throughout the energy range shown in the figure despite the fact that it is energetically accessible.

Fig. 2 Product vibrational state-resolved state-to-state reaction probabilities (J_tot = 0) of the H + DOH → HD + OH reaction with the DOH reactant in three different vibrational states: (a) DOH(000), (b) DOH(ν_OD = 1), and (c) DOH(ν_OH = 1). All the rotational states of the two products are summed. The bracket with two numbers (ν₁, ν₂) denotes the vibrational quantum numbers of the HD and OH products, respectively.

The decomposition of the total reaction probability from DOH(ν_OH = 1) is more interesting, as shown in Fig. 2(c). As expected for an OH spectator, both the (01) and (11) product vibrational states are populated starting from the same threshold as from DOH(000). Surprisingly, also present are the (00) and (10) product states, both with the OH product in its ground vibrational state, thus contradicting the spectator assumption for this mode. This accounts for the contribution to the total reaction probability in Fig. 1 at lower collision energies with a threshold of 0.4 eV. Furthermore, the feature in the total reaction probability from DOH(ν_OH = 1) is clearly why two segments with different slopes are present because they are contributed by different vibrational states of the OH product.

C. Vibrational mode specificity in differential cross sections

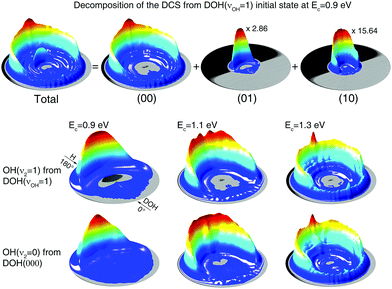
The differential cross section (DCS) represents the most detailed measurement of reaction dynamics, which resolves the angular distribution of the product ro-vibrational states, as shown in Fig. 3 as three-dimensional polar plots. The scattering angle is defined as the outgoing direction of the HD product relative to the direction of incoming H reactant. The radius in the plot represents the translational energy of the HD product in the center of mass frame, correlating to different ro-vibrational states of the HD and OH products by the laws of energy and momentum conservation.

Fig. 3 Three-dimensional polar plots of the DCS at three different collision energies for DOH(ν_OH = 1) and DOH(000). (Upper panel) Decomposition of the overall DCS to the contributions of different product vibrational channels. (Lower panel) DCSs of OH(ν₂ = 1) product from DOH(ν_OH = 1) reactant and OH(ν₂ = 0) product from DOH(000) reactant at the collision energies of 0.9, 1.1 and 1.3 eV.

Similar to the decomposition of the total reaction probability, the DCS can also be decomposed into contributions from different vibrational states of the HD and OH products, as shown in the upper panel of Fig. 3 for the DCS from DOH(ν_OH = 1) at the collision energy of 0.9 eV. At this collision energy, only the (00), (10), and (01) product states are energetically accessible, as shown in Fig. 2(c), so that the DCS at this energy is decomposed into the contributions from these three product states. It is clearly seen that the DCS is dominated by the (00) vibrational branch while the (01) state population is ∼3 times smaller, and that from the (10) state is ∼15 times smaller and is obscured by the contribution from the (01) state close in energy. Among them, the (01) product is expected from the spectator model. Since we are mostly interested in the spectator character of the non-reacting OH bond, we will focus on the (01) contribution. In the lower panel of Fig. 3, individual contributions of the (01) product channel from DOH(ν_OH = 1) and the (00) product channel from DOH(000) are compared at three collision energies. Generally, DCSs at the same collision energy are similar. At E_c = 0.9 eV, they are both peaked at the backward direction, which is consistent with the direct abstraction reaction mechanism. With the increase of collision energy, broader angular distributions start to appear but they are all backward centered. At E_c = 1.3 eV, noticeable forward distributions are both clearly seen from the two initial states. These results suggest that the non-reacting OH bond is well behaved as a spectator above 0.9 eV, as it not only sequesters the original vibrational energy but also shows nearly identical angular distributions in both cases.⁵²

The interesting discovery in Fig. 2(c) indicates that the OH(ν₂ = 0) product is produced from DOH(ν_OH = 1). This apparently contradicts the well-accepted OH spectator picture because the vibrational excitation of the OH mode in the DOH reactant is not carried over to the OH product. This surprising observation is worth some further investigation.

As can be seen in Fig. 2, at the energy within 0.4 eV above the threshold, only the (00) product vibrational state is produced for all the three initial states. This energy range is between 0.7 and 1.1 eV in total energy. To gain further insights, we compare in Fig. 4 DCSs from the three initial states at three total energies in this range. Surprisingly, at the same total energy, the DCSs show similar angular distributions even though the initial states have quite different vibrational features. The resemblance of DCSs between the DOH(000) and DOH(ν_OD = 1) states is understandable, as the reaction proceeds by channeling either translational or vibrational energy into the reaction coordinate. Since the OD stretching mode is an active mode with strong coupling with the reaction coordinate, the energy initially deposited into the OD stretching mode is efficiently used to promote the reaction by channeling its energy into the reaction coordinate and thus the memory of initial excitation is lost during the reaction.⁵⁵ This is the well-known ‘loss of memory’ effect of an active mode.⁵⁹ With the same threshold but different reaction probabilities between the DOH(000) and DOH(ν_OD = 1) states, as shown in Fig. 1(b), the reaction can be understood in such a picture that the same amount of translational and the OD vibrational energies can both facilitate the reaction but they differ by their efficacy in promoting the reaction, i.e., different amounts of incoming reactant flux that can pass the barrier. For the reactive flux that passed the barrier, the final state distribution is determined largely by the coupling between the product modes and the reaction coordinate at the transition state.^52,57,60,61 Due to the loss of initial state memory, it is not surprising to see similar angular distributions of product states in the DCSs from the two initial states.

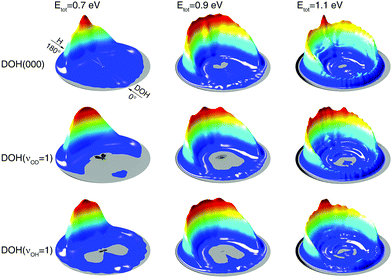Fig. 4 Three-dimensional polar plot of the DCSs from the DOH(000), DOH(ν_OD = 1), and DOH(ν_OH = 1) initial vibrational states at three total energies of 0.7, 0.9, and 1.1 eV.

On the other hand, the close resemblance of DCSs between the DOH(ν_OD = 1) and DOH(ν_OH = 1) initial states in Fig. 4 cannot be explained by the ‘loss of memory’ effect mentioned above, as the non-reacting OH bond is not an active mode. As shown in Fig. 2 the non-reacting OH bond does not behave as a spectator mode at the three total energies shown. To this end, it is interesting to see the angular distributions of the DCSs from DOH(ν_OH = 1) and DOH(ν_OD = 1) resemble each other, although the initial vibrational excitations are distinctly different.

Discussion

The above results display two seemingly conflicting behaviors of the non-reacting OH bond in reaction from the DOH(ν_OH = 1) initial state. At high energies, the non-reacting OH bond is shown to behave largely as a spectator by preserving the original vibrational excitation and showing almost same angular distribution in the DCS of OH(ν₂ = 1) from the DOH(ν_OH = 1) as the OH(ν₂ = 0) one from DOH(000). However, there also exists an unexpected channel evidently at low energies that the OH vibrational excitation is ‘quenched’ to form OH(ν₂ = 0) product from DOH(ν_OH = 1).

One straightforward and possible explanation of the surprising result of the OH(ν₂ = 0) product from DOH(ν_OH = 1) reactant is vibrational non-adiabaticity.^62–66 To this end, the coupling of the non-reacting mode with active ones allows energy flow between them in the entrance channel, resulting in energy loss in the former. For instance, the 100% threshold reduction in the theoretical investigation of the H + HCN(ν_CN = 1) → H₂ + CN reaction was attributed to vibrational non-adiabaticity.⁶³ In Fig. 1, all the vibrational excitation energy of DOH(ν_OH = 1) is used to reduce the threshold. In addition, the similar vibrational excitation of the CN product from HCN(004) and HCN(302) reacting with Cl atom was explained by vibrational non-adiabaticity as well.⁶⁷ Here in Fig. 4, the angular distribution of the DCS of DOH(ν_OH = 1) resembles the one from DOH(ν_OH = 1). These two observations both suggest the vibrational non-adiabaticity as the mechanism of the surprising result. According to this mechanism, the energy initially deposited in the OH stretching mode of the DOH reactant leaks out as H approaches, and the energy is used to overcome the reaction barrier. This results in the loss of vibrational excitation in the OH stretching mode, and subsequently the OH product in the ground vibrational state. This mechanism also predicts a lower reaction threshold. The OH stretching mode has a higher internal energy than the OD stretching mode by about 0.1 eV. After transferring the OH stretching energy to the OD stretching mode, there is an extra of 0.1 eV energy behaving as the translational energy. However, there is no direct evidence indicating energy leakage from DOH(ν_OH = 1).

To further investigate this issue, it is helpful to work in the local-mode regime,⁶⁸ which provides a natural paradigm for describing the vibrations in DOH and studying vibrational non-adiabaticity. Specifically, the three DOH vibrational states studied here are projected on to six local-mode stretching bases with the assumption that the bending is decoupled, and their weights are listed in Table 1. The two numbers in the local-mode states |(nm)〉 denote the stretching vibrational quantum numbers of the OD and OH bonds, respectively. It is shown in Table 1 that the (000) eigenstate is almost purely represented by the |(00)〉 local-mode state. Surprisingly, however, the DOH(ν_OD = 1) and DOH(ν_OH = 1) eigenstates are not solely represented by the |(10)〉 and |(01)〉, i.e., OD and OH stretching local-mode states, respectively. For example, the DOH(ν_OD = 1) eigenstate has a 11.37% contribution from the |(00)〉 local-mode state, while the DOH(ν_OH = 1) eigenstate has a contribution of 0.96% from the |(10)〉 local-mode state. It should be noted here that albeit small the |(10)〉 local-mode component might contribute remarkably due to its large reactivity.

Table 1 Weights of local-mode bases in the three vibrational eigenstates of the DOH reactant. The initial state ψ_i is written as a linear combination of the local-mode bases, i.e.

(νOD, νb, νOH)	|Cnm|^2
	|(00)〉	|(10)〉	|(01)〉	|(20)〉	|(02)〉	|(11)〉
(000)	99.66	0.18	0.15	0.00	0.00	0.00
(100)	11.37	87.54	0.58	0.36	0.00	0.15
(001)	0.22	0.96	98.32	0.02	0.32	0.15

---

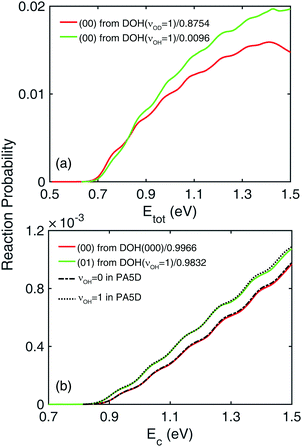
This interesting observation suggests that the small OD stretching (|(10)〉) local-mode component of the DOH(ν_OH = 1) state might actually contribute to the reactivity. In other words, the OD excited local-mode component (|(10)〉) in the DOH(ν_OH = 1) eigenstate will proceed to generate HD + OH with OH necessarily in the ground vibrational state. To demonstrate this possibility, the (00) product vibrational state-resolved reaction probabilities from the DOH(ν_OD = 1) and DOH(ν_OH = 1) initial states are plotted in Fig. 5(a), with normalization factors chosen as the weights of the |(10)〉 local-mode component in these two initial wavefunctions. These two curves are indeed quite similar, indicating that the contributing OD stretching is originated from the component already in the initial wave function, rather than from energy transferred from the OH stretching through vibrational non-adiabaticity. The contribution of the |(00)〉 and |(01)〉 local-mode components are negligible due to their small reactivity. At higher total energy above 1.0 eV, the difference between the two can be attributed to the fact that the |(20)〉 local-mode component also contributes to the forming of the (00) product states. This analysis argues against the vibrational non-adiabatic model, and attributes the additional reactivity to the local-mode excitation in the initial wavefunction.

Fig. 5 Product vibrational state-resolved state-to-state reaction probabilities (J_tot = 0) of the H + DOH → HD + OH reaction normalized by the weights of the corresponding local-mode components in the initial eigenstates. All the rotational states of the two products are summed. (a) The (00) product vibrational state-resolved reaction probabilities from the contribution of |(10)〉 local-mode component in the DOH(ν_OD = 1) and DOH(ν_OH = 1) initial states; (b) comparison of the state-to-state reaction probabilities in the spectator channel between full-dimensional and potential averaged five-dimensional (PA5D) calculations.

Another piece of evidence against vibrational non-adiabaticity is from the missing of the OH(ν₂ = 1) product from the DOH(ν_OD = 1) initial state, as shown in Fig. 2(b). If the vibrational non-adiabaticity were operative, energy initially deposited in the OD stretching mode could also flow into the OH stretching mode through non-adiabatic coupling. After passing the transition state, the excited OH stretching mode would result in the OH(ν₂ = 1) product.

To further provide evidence against vibrational non-adiabaticity, we take advantage of a reduced-dimensional model in which the non-reacting OH bond is excluded from the dynamical model, but its effect is considered as mean-field contribution through potential averaging by the one-dimensional ν_OH = 0 or 1 stretching vibrational wavefunction. In this way, the OH stretching mode in DOH is purely a local mode and fixed at one of the vibrational states throughout the reaction. This PA5D method has been shown to be quite accurate for this reaction when the reactant is in its ground vibrational state.²⁶ If vibrational non-adiabaticity were present, the PA5D results should be different from those obtained in full-dimensionality, because the former disallows energy flow into or out of the OH mode. To make a meaningful comparison, the reaction probabilities from the DOH(ν_OD = 1) and DOH(ν_OH = 1) initial states are again normalized with the weights of the appropriate local-mode components. In addition, a small energy shift of 0.003 eV is added, because the eigenstate of DOH reactant in the PA5D approximation is about 0.003 eV higher than the full-dimensional one. As shown in Fig. 5(b), the agreement between full- and reduced-dimensional results is excellent for both ν_OH = 0 and 1, ruling out vibrational non-adiabaticity as a possible mechanism for the H + DOH(ν_OH = 1) → HD + OH(ν₂ = 0) reaction.

It should be noted that the PA5D total reaction probability from the DOH(ν_OH = 1) initial state is quite different from the one shown in Fig. 1. The discrepancy is not due to the failure of this approximation but to the inaccuracy in representing the initial vibrational state of the DOH reactant, i.e., the missing of |(10)〉 and (|(00)〉) local-mode components. On the other hand, the total reaction probabilities from the DOH(000) initial state are similar between the full-dimensional calculation and the PA5D approximation. This is because the DOH(000) eigenstate is well represented in both cases due to the negligible vibrational excitation in the OH bond. Up to now, the PA5D approximation has only applied to the case when the spectator OH is in the ground vibrational state.²⁶ There is no limitation in applying this model to vibrationally excited OH spectator, but extra care should be taken to account for the initial eigenstate in full dimensionality.

In summary, the analysis above rules out vibrational non-adiabaticity as the origin of the OH(ν₂ = 0) production from the H + DOH(ν_OH = 1) → HD + OH(ν₂ = 0) reaction. Instead, it originates from a small component of the OD excited local-mode in the DOH(ν_OH = 1) initial wavefunction. The small weight of this local-mode component is compensated by its large reactivity.

Conclusions

In this work, we report a detailed analysis of the unexpected discovery of the OH(ν₂ = 0) product from the DOH(ν_OH = 1) initial state in the title reaction, using a state-to-state full-dimensional quantum dynamical method on an accurate PES. By taking advantage of the local-mode analysis and the decomposition of both the reaction probability and differential cross sections in terms of the product vibrational states, we identify correlations between initial and final states of the reaction. Two possible mechanisms are explored. One envisions non-adiabatic energy leakage from the spectator OH mode during the reaction, while the other assumes some OD excitation in the initial state. Our extensive analysis leads us to rule out the former mechanism of vibrational non-adiabaticity as the main cause of the surprising reactivity. Instead, we demonstrate that the phenomenon is due to small OD stretching (|(10)〉) local-mode component in the DOH(ν_OH = 1) initial state. The large reactivity of the OD excited initial state compensates its small weight, rendering a substantial contribution. In other words, the mixing of states exists in the initial state rather than during the reaction.

These results reaffirm that the non-reacting OH bond in the DOH reactant behaves perfectly as a spectator no matter it is initially prepared in the vibrational ground or first excited state. This lends support to the commonly accepted notion that for reactions involving larger molecules, the site of reaction only contains a small number of active modes and the remaining ones are all behaved largely as spectators.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

Z. B. thanks Alexander von Humboldt-Stiftung for a Fellowship and Prof. Uwe Manthe for useful discussions. This work was supported by the US Department of Energy (Grant No. DE-SC0015997 to H. G.) and by the National Natural Science Foundation of China (Grant No. 21222308, 21133006 and 21433009 to Z. S.). Part of the calculations were performed at the Center for Advance Research Computing (CARC) at University of New Mexico.

References

1. S. C. Althorpe and D. C. Clary, Annu. Rev. Phys. Chem., 2003, 54, 493–529.
2. W. Hu and G. C. Schatz, J. Chem. Phys., 2006, 125, 132301.
3. D. C. Clary, Proc. Natl. Acad. Sci. U. S. A., 2008, 105, 12649.
4. D. H. Zhang and H. Guo, Annu. Rev. Phys. Chem., 2016, 67, 135–158.
5. K. Liu, Adv. Chem. Phys., 2012, 149, 1–46.
6. B. Joalland, Y. Shi, A. D. Estillore, A. Kamasah, A. M. Mebel and A. G. Suits, J. Phys. Chem. A, 2014, 118, 9281–9295.
7. K. Liu, Annu. Rev. Phys. Chem., 2016, 67, 91–111.
8. F. F. Crim, Acc. Chem. Res., 1999, 32, 877–884.
9. M. A. Collins, Theor. Chem. Acc., 2002, 108, 313–324.
10. J. M. Bowman, G. Czakó and B. Fu, Phys. Chem. Chem. Phys., 2011, 13, 8094–8111.
11. B. Jiang, J. Li and H. Guo, Int. Rev. Phys. Chem., 2016, 35, 479–506.
12. B. Zhao and H. Guo, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2017, 7, e1301.
13. J. Li, B. Jiang, H. Song, J. Ma, B. Zhao, R. Dawes and H. Guo, J. Phys. Chem. A, 2015, 119, 4667–4687.
14. A. Sinha, M. C. Hsiao and F. F. Crim, J. Chem. Phys., 1991, 94, 4928–4935.
15. A. Sinha, J. D. Thoemke and F. F. Crim, J. Chem. Phys., 1992, 96, 372–376.
16. M. J. Bronikowski, W. R. Simpson and R. N. Zare, J. Phys. Chem., 1993, 97, 2194–2203.
17. M. J. Bronikowski, W. R. Simpson and R. N. Zare, J. Phys. Chem., 1993, 97, 2204–2208.
18. B. R. Strazisar, C. Lin and H. F. Davis, Science, 2000, 290, 958–961.
19. I. W. M. Smith and F. F. Crim, Phys. Chem. Chem. Phys., 2002, 4, 3543.
20. C. Xiao, X. Xu, S. Liu, T. Wang, W. Dong, T. Yang, Z. Sun, D. Dai, X. Xu, D. H. Zhang and X. Yang, Science, 2011, 333, 440–442.
21. S. Liu, C. Xiao, T. Wang, J. Chen, T. Yang, X. Xu, D. H. Zhang and X. Yang, Faraday Discuss., 2012, 157, 101–111.
22. R. P. A. Bettens, M. A. Collins, M. J. T. Jordan and D. H. Zhang, J. Chem. Phys., 2000, 112, 10162.
23. G.-S. Wu, G. C. Schatz, G. Lendvay, D. C. Fang and L. B. Harding, J. Chem. Phys., 2000, 113, 3150–3161.
24. M. Yang, D. H. Zhang, M. A. Collins and S.-Y. Lee, J. Chem. Phys., 2001, 115, 174–178.
25. J. Chen, X. Xu, X. Xu and D. H. Zhang, J. Chem. Phys., 2013, 138, 154301.
26. D. H. Zhang and J. Z. H. Zhang, J. Chem. Phys., 1994, 101, 1146–1156.
27. D. Neuhauser, J. Chem. Phys., 1994, 100, 9272–9275.
28. U. Manthe, T. Seideman and W. H. Miller, J. Chem. Phys., 1993, 99, 10078–10081.
29. J. Dai, W. Zhu and J. Z. H. Zhang, J. Phys. Chem., 1996, 100, 13901–13903.
30. W. Zhu, J. Dai, J. Z. H. Zhang and D. H. Zhang, J. Chem. Phys., 1996, 105, 4881–4884.
31. D. H. Zhang and J. C. Light, J. Chem. Phys., 1996, 104, 4544–4553.
32. D. H. Zhang and J. C. Light, J. Chem. Phys., 1996, 105, 1291–1294.
33. D. H. Zhang and J. C. Light, J. Chem. Soc., Faraday Trans., 1997, 93, 691–697.
34. D. H. Zhang, M. A. Collins and S.-Y. Lee, Science, 2000, 290, 961–963.
35. D. H. Zhang, M. Yang and S.-Y. Lee, J. Chem. Phys., 2001, 114, 8733.
36. D. H. Zhang, D. Xie and M. Yang, Phys. Rev. Lett., 2002, 89, 283203.
37. E. M. Goldfield and S. K. Gray, J. Chem. Phys., 2002, 117, 1604.
38. P. Defazio and S. K. Gray, J. Phys. Chem. A, 2003, 107, 7132–7137.
39. J. Mayneris, M. Gonzalez and S. K. Gray, Comput. Phys. Commun., 2008, 179, 741–747.
40. M. T. Cvitaš and S. C. Althorpe, J. Phys. Chem. A, 2009, 113, 4557.
41. M. T. Cvitaš and S. C. Althorpe, J. Chem. Phys., 2011, 134, 024309.
42. B. Jiang, D. Xie and H. Guo, J. Chem. Phys., 2011, 135, 084112.
43. M. T. Cvitaš and S. C. Althorpe, J. Chem. Phys., 2013, 139, 064307.
44. B. Fu and D. H. Zhang, J. Chem. Phys., 2013, 138, 184308.
45. B. Zhao, Z. Sun and H. Guo, J. Chem. Phys., 2014, 141, 154112.
46. B. Fu and D. H. Zhang, J. Chem. Phys., 2015, 142, 064314.
47. B. Zhao, Z. Sun and H. Guo, J. Chem. Phys., 2016, 144, 064104.
48. B. Zhao, Z. Sun and H. Guo, J. Chem. Phys., 2016, 144, 214303.
49. S. Liu, X. Xu and D. H. Zhang, J. Chem. Phys., 2012, 136, 144302.
50. S. Liu and D. H. Zhang, Chem. Sci., 2016, 7, 261–265.
51. Z. Zhao, S. Liu and D. H. Zhang, J. Chem. Phys., 2016, 145, 134301.
52. B. Zhao, Z. Sun and H. Guo, J. Chem. Phys., 2016, 145, 134308.
53. B. Zhao, Z. Sun and H. Guo, J. Chem. Phys., 2016, 145, 184106.
54. J. C. Polanyi, Science, 1987, 236, 680–690.
55. H. Guo and K. Liu, Chem. Sci., 2016, 7, 3992–4003.
56. H. Guo and B. Jiang, Acc. Chem. Res., 2014, 47, 3679–3685.
57. B. Zhao, Z. Sun and H. Guo, J. Am. Chem. Soc., 2015, 137, 15964–15970.
58. B. Jiang and H. Guo, J. Am. Chem. Soc., 2013, 135, 15251–15256.
59. R. Welsch and U. Manthe, J. Phys. Chem. Lett., 2015, 6, 338–342.
60. B. Zhao, Z. Sun and H. Guo, J. Chem. Phys., 2015, 142, 241101.
61. C. Xie, B. Jiang, M. Yang and H. Guo, J. Phys. Chem. A, 2016, 120, 6521–6528.
62. W. T. Duncan and T. N. Truong, J. Chem. Phys., 1995, 103, 9642–9652.
63. T. Takayanagi and G. C. Schatz, J. Chem. Phys., 1997, 106, 3227–3236.
64. L. Halonen, S. L. Bernasek and D. J. Nesbitt, J. Chem. Phys., 2001, 115, 5611–5620.
65. S. Yoon, S. Henton, A. N. Zivkovic and F. F. Crim, J. Chem. Phys., 2002, 116, 10744–10752.
66. S. Yan, Y.-T. Wu and K. Liu, Proc. Natl. Acad. Sci. U. S. A., 2008, 105, 12667–12672.
67. J. M. Pfeiffer, R. B. Metz, J. D. Thoemke, E. Woods and F. F. Crim, J. Chem. Phys., 1996, 104, 4490–4501.
68. M. S. Child and L. Halonen, Adv. Chem. Phys., 1984, 57, 1–58.

---

Footnotes

† Electronic supplementary information (ESI) available: Parameters used in the calculations and additional results. See DOI: 10.1039/c7cp07199j

‡ Present address: Theoretische Chemie, Fakultät für Chemie, Universität Bielefeld, Universitätsstr. 25, D-33615 Bielefeld, Germany.

---