Detection of the electronic structure of iron-(III)-oxo oligomers forming in aqueous solutions

Abstract

The nature of the small iron-oxo oligomers in iron-(III) aqueous solutions has a determining effect on the chemical processes that govern the formation of nanoparticles in aqueous phase. Here we report on a liquid-jet photoelectron-spectroscopy experiment for the investigation of the electronic structure of the occurring iron-oxo oligomers in FeCl₃ aqueous solutions. The only iron species in the as-prepared 0.75 M solution are Fe³⁺ monomers. Addition of NaOH initiates Fe³⁺ hydrolysis which is followed by the formation of iron-oxo oligomers. At small enough NaOH concentrations, corresponding to approximately [OH]/[Fe] = 0.2–0.25 ratio, the iron oligomers can be stabilized for several hours without engaging in further aggregation. Here, we apply a combination of non-resonant as well as iron 2p and oxygen 1s resonant photoelectron spectroscopy from a liquid microjet to detect the electronic structure of the occurring species. Specifically, the oxygen 1s partial electron yield X-ray absorption (PEY-XA) spectra are found to exhibit a peak well below the onset of liquid water and OH⁻ (aq) absorption. The iron 2p absorption gives rise to signal centered between the main absorption bands typical for aqueous Fe³⁺. Absorption bands in both PEY-XA spectra are found to correlate with an enhanced photoelectron peak near 20 eV binding energy, which demonstrates the sensitivity of resonant photoelectron (RPE) spectroscopy to mixing between iron and ligand orbitals. These various signals from the iron-oxo oligomers exhibit maximum intensity at [OH]/[Fe] = 0.25 ratio. For the same ratio, we observe changes in the pH as well as in complementary Raman spectra, which can be assigned to the transition from monomeric to oligomeric species. At approximately [OH]/[Fe] = 0.3 we begin to observe particles larger than 1 nm in radius, detected by small-angle X-ray scattering.

---

1. Introduction

Iron-(III)-based oxides, oxohydroxides, and hydroxides (short iron-(III) oxides) are among the most important environmental metal compounds, playing a major role in biological processes and technology. In nature, these metal oxides assist in controlling the pH of surface-, ground-, and sea water, and also influence microbiological activity or sorption of nutrients and trace elements.^1–6 Technological applications are diverse, and include utilization in medicine,⁷ magnetic storage,^8,9 sensing,^10–12 as well as catalysis.^13,14 Given their wide impact iron oxides have been intensively studied experimentally and theoretically, with focus on both the transformation of atomic Fe³⁺ into Fe_nO_xH_y oligomers (here referred to as seeds) in aqueous solution, and on the characterization of the solid-phase aggregates and crystals (referred to as particles) which form upon subsequent agglomeration. At very low pH the dominant iron complex in FeCl₃ aqueous solution is (Fe[H₂O]₅OH)²⁺, followed by (Fe[H₂O]₆)³⁺ and other monomeric iron complexes including the anions of the salt that is being used, mostly FeCl₃ or Fe(NO₃)₃. Nucleation is initiated by neutralization upon addition of OH⁻ molecules that bind with Fe³⁺ ions. The thus formed iron-hydroxyl monomers diffuse, and form dimers and probably larger oligomers, which at large enough OH⁻ concentration aggregate into iron-polymeric seeds.^15–18 Any of these processes can be controlled by the [OH]/[Fe] ratio (=h, following the notation in ref. 19), which depends on the base that is used, typically NaOH or the weaker base NaHCO₃, and on the concentration of the iron salt.

The solid-phase products, forming for h > 0.5 in iron aqueous solutions, have been exhaustively studied to explore structure, size, and morphology.^{15,16,18–25} Experimental methods applied include titration, UV-vis spectroscopy,^26,27 wide- and small-angle X-ray scattering (WAXS and SAXS),^19,28,29 X-ray absorption (XA) spectroscopy,^{19,20,23,24,26,29–32} and electron microscopy.³³ In the case of FeCl₃ aqueous solutions, the different experiments find that akaganeite (β-FeOOH) forms, for h > 0.5.^1,25,34 Chloride ions were concluded to have a structure-driving effect during formation of akaganeite,^20,35–38 and yet the exact mechanism remains to be resolved. One likely scenario is that the Cl⁻ ion is incorporated into the structure at the stage of polynuclear complex formation, and is released when larger aggregates form.³⁸ Another work assigns Cl⁻ to defined positions in the mono- and polynuclear complexes.^20,24,39 With further polymerization edge- and corner-sharing clusters, stabilized by Cl⁻, were proposed. Eventually, cylindrically-shaped akaganeite seeds form, possibly stabilized by Cl⁻ in the inner coordination spheres. At yet further advanced aggregation more complex shapes are adopted, with only little amount of Cl⁻ in the very vicinity of iron. These observations are in agreement with very recent molecular dynamics simulations exploring counter-ion specific effects.¹⁸ Cl⁻ is suggested to accommodate in the first solvation shell, thereby favoring a chain-like polymeric structure during condensation reactions. In the absence of Cl⁻–iron interactions, on the other hand, ring-like structures are favored.

Unlike the formation of particles, our understanding of the transformation of monomeric Fe-oxohydroxy species in FeCl₃ aqueous solution, occurring for h < 0.5, is surprisingly poor. In fact, there is not even an unequivocal experimental evidence for the existence of iron oligomers larger than the dimer, although the occurrence of trimers has been suggested.^{16,18,20,31,32} The uncertainty regarding the existence of the larger oligomers is due to the different experimental conditions that have been applied to probing the liquid solutions. Early X-ray absorption spectroscopy measurements were conducted from freeze-dried FeCl₃ aqueous solutions, 0 < h < 2.8.^20,24,39 In those studies monomeric iron species, FeCl₂(H₂O)₄, have been identified, and the subsequent elimination of Cl⁻ from the first solvation shell was observed for increased polymerization. The authors further concluded that the monomeric species condense into iron dimers as well as trimers.²⁰ A very recent in situ XA spectroscopy study combined with density functional theory (DFT) electronic structure calculations suggests that Fe μ-oxo bridged dimers form in the case of Cl⁻ as well as for NO₃⁻ and ClO₄⁻, not though for SO₄²⁻, in a pH range of 1.0–2.2.³¹ Based on their computations the authors speculate that there could be also a significant concentration of iron trimers during hydrolysis, but as noted above there is no unambiguous experimental evidence. A similar conclusion has been drawn from a combined X-ray (again in situ), UV-vis, and Mössbauer-spectroscopy study on the precipitation pathways for ferrihydrite formation in acidic solution from iron nitrate.¹⁹ The authors have shown that iron exists mainly as monomer, μ-oxo aqua dimers, and the solid ferrihydrite. Again, no larger iron-oxo oligomers were detected, suggesting the reconfiguration of the μ-oxo dimer structure prior to further nucleation.

Up to this point we have not accounted for the lifetimes of the iron-oxo oligomers which may be too short for these species to be detected with the aforementioned experimental techniques that probe minutes or hours after solution preparation. In a theoretical molecular dynamics simulation of iron solutions the reactions beyond dimer formation were indeed found to happen in just tens of picoseconds.¹⁸ Also, experiments on iron perchlorate solutions report fast rate constants for dimer formation of 400 M⁻¹ s⁻¹ implying that the larger oligomers form rapidly as well.^1,40 Such fast kinetics will affect the subsequent nucleation and aggregation reactions, and suggests that small iron oligomers, dimers, trimers, tetramers, and perhaps even larger ones, are too short-lived to be detected. We note that unlike for other metal ions, such as Cr³⁺, Al³⁺, or Rh³⁺, reactions are particularly fast for Fe³⁺.^41,42

In the present study, we measured soft-X-ray photoelectron (PE) spectra from a liquid microjet to determine the electronic structure of the iron-oxo species in FeCl₃ aqueous solution, for h < 0.5. That is, unlike most previous X-ray studies, experiments are conducted directly from the aqueous solution rather than from dried phase. Furthermore, we here detect emitted electrons rather than transmitted or scattered X-rays. This is also the first X-ray (photoemission) study detecting signal from iron-oxo oligomers at the oxygen 1s edge.

Measurements were performed for non-resonant and resonant photon energies, where the latter refers to excitations at the oxygen 1s (near 530 eV photon energy) and Fe 2p (near 705 eV) edges, respectively. This is also different from any previous works, reporting Fe 1s-edge transmission XA spectra, and more importantly, in measuring photoelectron spectra also from oxygen complementary important spectroscopic information is obtained. By integration of the signal of the resonant photoelectron (RPE) spectra we generate the so-called partial-electron-yield X-ray absorption (PEY-XA) spectra. To first approximation these spectra are a good representation of the actual X-ray absorption which would be accurately measured in X-ray transmission,⁴³ and the assumption is that the absorption is proportional to the number of emitted Auger electrons.⁴³ By comparing PEY-XA spectra from the partially hydrolyzed solutions with the spectrum from Fe³⁺ (aq), obtained from the FeCl₃ solution with no OH⁻ added, we unequivocally determine the X-ray absorption of the iron-oxo oligomers. Yet, more important, from the respective RPE spectra we directly identify the valence orbitals, and their mixed iron–oxygen character, which are responsible for the absorption. To support our interpretation of the PE and the PEY-XA spectra we also conducted Raman and small-angle X-ray scattering (SAXS) measurements from the same aqueous solutions. Raman spectra are compared with reported spectra from well characterized iron–oxide phases to identify and assign structure motifs of the oligomers. SAXS, on the other hand is used to detect particles, and most important for this study the h ratio at which small particles begin to form can be determined.

2. Experimental

2.1. Preparation of iron aqueous solutions

Stock solutions of 1.9 M FeCl₃·6H₂O and 3.8 M NaOH were prepared from FeCl₃·6H₂O (purity ≥ 99%; Sigma Aldrich) powder and NaOH pellets (purity ≥ 98%; Sigma Aldrich) without further purification. Water (Millipore; 18.2 MΩ cm⁻¹) was flushed with nitrogen for >12 h before being used. The final concentration of the FeCl₃·6H₂O solution studied here was 0.75 M. [OH]/[Fe] (=h) ratios, from 0–2.5, were adjusted by addition of a defined amount of NaOH solution to water, and this solution is then added to a constant fraction of FeCl₃·6H₂O under vigorous stirring. A scheme of the preparation procedure is shown in Fig. SI-1 (ESI†), and the mixing ratios of the different solutions are presented in Table SI-1 (ESI†). For the photoelectron-spectroscopy experiments 100 ml solutions were prepared, whereas for Raman and SAXS measurements 5 ml were sufficient.

For each aqueous solution, i.e., for each h, the pH was measured for different (aging) times, 15 min, 1 h, and 24 h, after preparation. We used an InLab Semi-Micro-L pH electrode (Mettler Toledo, Gießen, Germany) which was calibrated with buffer solutions of pH 2.00, 4.01 and 7.00.

2.2. Photoelectron spectroscopy measurements

Photoelectron spectroscopy measurements were performed at the U49/2-PGM-1 soft-X-ray undulator beamline at the synchrotron radiation facility BESSY II in Berlin, Germany. The liquid microjet with a diameter of 24 μm was injected into the vacuum chamber from a fused-silica nozzle. The jet velocity was approximately 40 ms⁻¹, and the jet temperature was kept at 8 °C. Details of the liquid microjet technique and of the experimental setup have been described previously.^44–46 The energy resolution of the U49/2-PGM-1 beamline was better than 250 meV at 530 eV photon energy used for the oxygen O 1s resonant valence PE measurements, and ∼380 meV at 710 eV photon energy needed for the PE measurements at the Fe 2p_3/2 absorption edge. This beamline provides a suitably small focal size of 20 × 80 μm² at high photon flux, assuring that the (water) gas-phase signal contribution to the total (photo)electron signal is much smaller than the signal from aqueous phase. The energy resolution of the hemispherical electron analyzer, ∼250 meV at 30 eV pass energy, was constant with kinetic energy (KE). Oxygen 1s resonant spectra were calibrated with reference to the water valence 1b₁ peak, which is 11.31 eV binding energy, and Fe 2p_3/2 resonant spectra were calibrated against the O 1s binding energy of water, which is 538.1 eV.^47,48

2.3 Raman spectroscopy measurements

Raman spectra were collected for aqueous solutions in the range of 0.0 ≤ h ≤ 2.5. Measurements were performed with a LabRam HR800 spectrometer (Horiba Jobin Yvon, Bensheim, Germany), equipped with a 633 nm HeNe laser (Horiba Jobin Yvon, Bensheim, Germany), a 300 lines per mm grating, and a BX41 microscope (Olympus, Hamburg, Germany). The back-scattered Raman light was collected by a liquid nitrogen-cooled CCD detector (1024 × 256 pixels, Horiba). Using a 60× immersion objective, the laser intensity at the liquid sample was 5.09 × 10⁵ W cm⁻². Reported Raman spectra are averages of five sweeps, each recorded with an acquisition time of 10 s. All measurements were performed 1 h after solution preparation.

2.4 Small-angle X-ray scattering measurements

Scattering curves were measured for 0.05 ≤ h ≤ 1 using a laboratory SAXS instrument (SAXSess, Anton Paar, Graz, Austria), equipped with a sealed X-ray tube (Cu anode target, λ = 1.5406 Å). A flow-quartz capillary with a thickness of 1 mm was used as sample holder. SAXS data from the hydrolyzed solutions are presented with the spectrum measured for h = 0 subtracted and were corrected for the slit smearing effect. Data were fitted to scattering curves within a cylinder model and a Schulz distribution for the radius, using the SANS Analysis_v3.00 tool implemented in the software package IGOR PRO.⁴⁹ More information about the fitting model can be found in the ESI.†

3. Results and discussion

We first present the evolution of pH as function of both h and time. This is followed by a presentation and discussion of the various photoemission spectra, i.e., on- and off-resonant valence PE spectra, and the resulting PEY-XA spectra. We then show results from Raman and SAXS measurements, and discuss the complementary information one obtains on the structure of the iron-oxo oligomers and their aggregation.

3.1 pH dependence on h and aging time

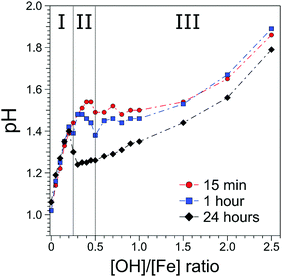
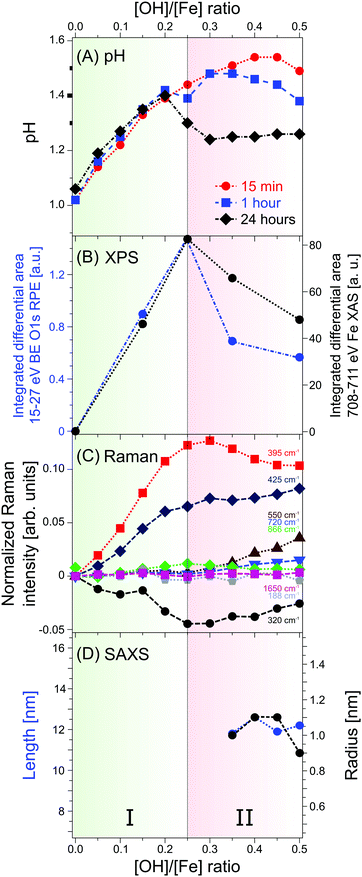
The [OH]/[Fe] = h ratios and pH are directly connected, and the quantitative relation provides a first qualitative hint at the role OH⁻ plays in the nucleation and aggregation processes. Results are shown in Fig. 1, where we present pHs for 0 < h < 2.5, measured for different aging times, from 15 min to 24 h. For all aging times studied pH rises steeply from 1.0 to 1.4 for a very small initial increase of h, from 0 to 0.2, marked as region I in the figure. Time depending aging effects set in at h > 0.2 as will be discussed below. The solutions measured 15 min after preparation exhibit a continuous steady increase of pH in the region of 0.25 < h < 0.5; this is region II in the figure. For h > 0.5 the pH stays rather constant (near 1.5) up to h = 1.5, upon further addition of NaOH, corresponding to h > 1.5 pH rises again. We call this region III, explored here up to h = 2.5. The behavior of the 60 min solutions is rather similar, but the plateau (region II) appears to set in somewhat earlier, at h = 0.3, and pH is slightly smaller (≈1.45) than for the 15 min solution. More prominent differences occur for the 24 hour solutions, where the pH suddenly drops from 1.4 to approximately 1.2, right at the border between regions I and II, and then steadily rises through regions II–III, but the solutions stay always more acidic than for the shorter aging times. The observed time-independent pH increase (region I) implies that not all OH⁻ molecules are being consumed in the formation of iron-hydroxide complexes, but rather neutralize protons (H₃O⁺ (aq)) to form water. The time independent behavior further suggests that stable compounds, most likely monomeric iron-(III) complexes exist in region I. The time-dependent pHs (regions II–III), on the other hand must be assigned to an increasing consumption of OH⁻ the longer the reaction proceeds, which we tentatively attribute to the formation of iron-oxide hydroxide polynuclear compounds (transition region I–II) and particles (region II–III). The SAXS measurements indicate that particles begin to form in region II. The constant and reduced pH (region III) can be explained by an exchange of Cl⁻ and H₂O in the complexes for OH⁻ from solution. Alternatively, one can envision an indirect process where added OH⁻ are neutralized by protons stemming from condensation reactions of iron monomers or from deprotonation reactions of the clusters. From our discussion of the pH behavior we then expect to detect iron-oxo oligomers at the transition from region I to II, i.e., in a regime where particles are yet absent, and the concentration of the seeds being probably largest.

Fig. 1 Evolution of pH of 0.75 M FeCl₃ solutions as a function of h = [OH]/[Fe] ratio. Regions I–III correspond to the transitions from monomeric iron species to iron-oxo oligomers, and finally iron-oxo solid particles. Region I: oligomers with <1 nm diameter. Region II: cylindrical particles. Region III: cylindrical particles and akaganeite formation.

3.2 Photoemission spectra from solutions

Oxygen-1s resonant PE spectra and PEY-XA spectra. Fig. 2A presents partial electron yield X-ray absorption (PEY-XA) spectra at the oxygen 1s edge, covering the 527–547 eV photon energy range, from 0.75 M FeCl₃ solutions for h = 0, 0.15, 0.25, 0.35, and 0.5. For comparison, PEY-XA spectra are also shown from neat liquid water as well as from 35% NaOH aqueous solution. The spectra are obtained by integration of the respective valence resonant photoemission signal intensities in the 470–530 eV kinetic-energy range; a given PEY-XA spectrum thus results from the intensity changes among the RPE spectra.⁵⁰ More precisely, the signal due to emission of Auger electrons that overlaps with the valence photoelectron spectrum (at resonance) is approximately proportional to the X-ray absorption.⁴³ But more interesting is the fact that the intensity of photoelectron peaks that correspond to the ionization of a given orbital can get enhanced due to the interference of Auger electron and direct photoelectron channels. By such a signal enhancement we can then identify the overlap of orbitals (or electron delocalization)^50,51 from the oligomers and water, and obtain valuable insight into electronic-structure interactions.

Fig. 2 (A) Oxygen 1s PEY-XA spectra from FeCl₃ solutions for h = 0, 0.15, 0.25, 0.35, 0.5. For comparison, spectra from neat water (in blue) and from a 35 wt% NaOH aqueous solution (in green) are also presented. The low-energy shoulder on the 535 eV pre-peak visible in all spectra is due to gas-phase water. The inset shows an enlarged view of the spectral region of a centered at 529.5 eV photon energy. (B) Resonant valence PE spectra measured at 529.5 eV from the same 0.75 M FeCl₃ aqueous solutions, 0 ≤ h ≤ 0.5, as in (A). Spectra were energy-calibrated with the help of the 1b₁ energy of water, and intensities are displayed such that the height of the Cl⁻ 3p peak at 9.6 eV binding energy is the same. The reference spectrum from the h = 0 solution (in blue at bottom) is reproduced in all traces to highlight the spectral differences as a function of h (blue-shaded areas). The sketch at left indicates the formation of the iron-oxo oligomers with increasing h.

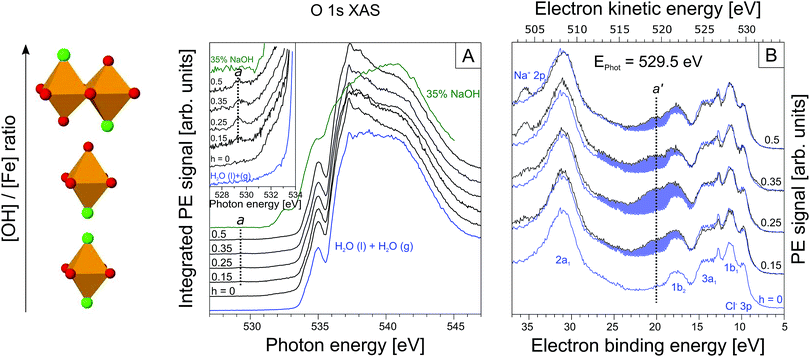
From Fig. 2A we see that the PEY-XA spectra from the iron aqueous solutions are very similar to the neat-water XA spectrum with its characteristic pre-edge at 535.0 eV, main edge (538.0 eV), and post-edge (541.0 eV).⁵² The most important, although very small spectral difference though is the intensity growing in near 529.5 eV (referred to as peak a), which is well below the water XA onset; an enlarged view of this spectral region is presented in the inset of Fig. 2A. Absorption a clearly arises from some iron-oxide species. Spectral contribution from OH⁻ (aq) can be ruled out; the lowest-energy absorption for the NaOH aqueous solution (in green) is at 532.5 eV. We also note that the first-hydration-shell water molecules in (Fe(H₂O)₆)³⁺ (aq) absorb at considerably larger energy than a, at 531.0 eV.⁵³ Another important observation from the inset in Fig. 2A is that peak a only exists in a small h window, exhibiting maximum intensity at h = 0.25. With reference to Fig. 1, this is exactly the ratio at which the transition from time-independent to time-dependent behavior of pH (going from I to II) is observed. In Section 3.1 we have argued that this is the region where the oxo-oligomers have not yet aggregated to form particles.

Up to this point we have solely evaluated the O 1s PEY-XA spectra without aid of the respective RPE spectra. As aforementioned the PEY-XA spectra are proportional to the emitted Auger-electron intensities at resonance, but there is an additional signal contribution which manifests in an intensity increase of certain binding energy features in the RPE spectra. These are fingerprints of oxygen–iron orbital mixing⁴³ which we will explain when presenting the RPE spectra measured at the photon energy 529.5 eV, corresponding to absorption a. Results are shown in Fig. 2B for the same solutions, i.e. same h ratios, as in Fig. 2A. The bottom spectrum (in blue) is essentially the valence PE spectrum of neat liquid water with its four valence orbitals, 1b₁ (11.31 eV binding energy), 3a₁ (13.5 eV BE), 1b₂ (17.5 eV BE), and 2a₁ (30.5 eV BE).^47,54 Contributions from FeCl₃ are small; the only noticeable signal is the Cl⁻ 3p doublet at 9.6 eV.^55–58 The small electron signal from Fe³⁺ 3d ionization is partially hidden underneath the 1b₁ peak of water.^59,60 When increasing the OH⁻ concentration to yield h = 0.15 one observes the appearance of a broad spectral feature in the 17–27 eV BE range. The largest intensity increase occurs at 21 eV BE, labeled a′ in the figure. This spectral region can be assigned to O 1s spectator Auger decay, and refers to the promotion of an O 1s electron (at 529.5 eV excitation energy) of an iron-oxo oligomer to an unoccupied molecular state below the vacuum level. The O 1s core-hole is subsequently refilled by a valence electron within the few-femtoseconds lifetime, and the released energy is used to eject another valence electron into vacuum.^61,62 To further characterize the iron-oxide oligomers that give rise to XA-peak a, and which are also responsible for PE peak a′ we need to also investigate the iron resonances. Here, we are particularly interested in a signature of a′, associated with oxygen–iron mixed orbitals.

Iron-2p resonant PE spectra and PEY-XA spectra. Fig. 3A presents PEY-XA spectra at the iron 2p edge (only 2p_3/2 was measured) from the same solutions for which O 1s spectra (Fig. 2A and B) have been recorded. The spectrum from the h = 0 solution (in blue) is reproduced in each tier so that the spectral changes become more visible. Spectra were obtained by signal integration of the (valence) resonant PE spectrum measured at the respective photon energy, varied here from 706.5 to 717.0 eV. The integration range of the RPE spectra was 6–43 eV BE (equivalent to ∼660–700 eV KE) which covers the region of the 2p–3d3d Auger-electron emission. All XA spectra exhibit the double-peak structure characteristic of Fe³⁺, i.e., a smaller pre-peak near 708.9 eV and main peak at 710.7 eV photon energy. These absorptions result from the excitation of an Fe 2p_3/2 electron into the t_2g and e_g valence levels, respectively, of the octahedrally coordinated iron cation.^50,63,64 The intensity giving rise to the asymmetric shoulder near 712 eV photon energy is commonly attributed to charge-transfer states between the iron and the ligand;^50,65 for h = 0 the ligands are the hydration water molecules. As seen in Fig. 3A, the most noticeable spectral change as a function of h is a signal increase occurring between 709.0 and 710.4 eV excitation energy. The difference spectrum, h = 0.25 solution minus h = 0 solution, presented in the inset of Fig. 3A, reveals an absorption band (labeled b) with a maximum at 709.6 eV. Absorption b is largest for h = 0.25–0.35 which is the same range where we find the O 1s absorption, a, suggesting that iron absorption b originates from the same species. To demonstrate that this is indeed the case we next explore the iron 2p RPE spectra. Fig. 3B presents the 709.6 eV (absorption b′) RPE spectra for h = 0.25 and h = 0, respectively. The important observation is a slightly larger signal intensity near 20 eV BE for the former solution. This feature is similarly broad and is also located at the very similar binding energy as a′ in the O 1s RPE spectra which not only confirms that O 1s and Fe 2p spectroscopies probe the same iron-oxo species, it also reveals the hybridization between iron and oxygen orbitals. Structure information is revealed from our Raman measurements discussed next.

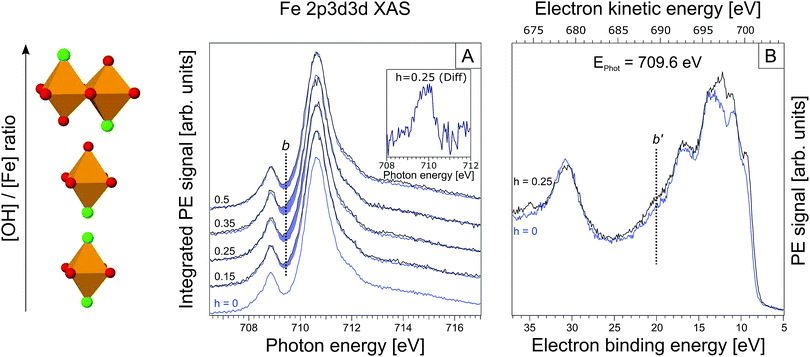Fig. 3 (A) Partial electron yield X-ray absorption spectra at the iron 2p_3/2. The h = 0 XA spectrum is reproduced in each tier for h ≠ 0. Again, spectral differences are highlighted in blue. The inset displays the actual differential spectrum for h = 0.25; b is the maximum of this absorption band. (B) RPE spectrum for h = 0.25 solution, measured at 709.6 eV excitation photon energy (maximum of the main absorption band in Fig. 3A). In blue the RPE spectrum for h = 0 is shown.

3.3 Raman measurements

Raman spectra, recorded for 0.75 M FeCl₃ with 0 < h < 2.5, are shown in Fig. SI-2 (ESI†). Fig. SI-2A (ESI†) presents the measured spectra from which a linear background, determined from extrapolation of the linear slope between 1100 cm⁻¹ and 1550 cm⁻¹, has been subtracted. The spectra are also displayed to yield the same peak height at 188 cm⁻¹; Fig. SI-2B (ESI†) shows the same spectra but with the h = 0 reference spectrum subtracted. The spectra of FeCl₃ (aq) with no NaOH added (h = 0) in Fig. SI-2A (ESI†) exhibit the Raman bands characteristic for ferric chloride, at 188 cm⁻¹, 320 cm⁻¹, 480 cm⁻¹, and 1650 cm⁻¹.⁶⁶ Bands below 200 cm⁻¹ are the translational vibrations of hydrogen bonded H₂O–H₂O or Cl–H₂O motifs.^66,67 The 320 cm⁻¹ band is generally assigned to Fe–Cl stretching vibrations,^66,68,69 and the shoulder at 440–480 cm⁻¹ is due to the Fe–OH₂ stretch.⁶⁶ The broad band at 1650 cm⁻¹ corresponds to the water ν₂ bending vibration.^67,70 In contrast, Raman spectra measured at the large ratio h = 2.5 exhibit additional bands characteristic for akaganeite, at 395 (Fe–OH), 550 and 720 cm⁻¹ (FeOOH).⁶⁹ Furthermore, the occurrence of a band at 866 cm⁻¹ with maximum intensity near h = 0.25 can be probably assigned to Fe–O–Fe motifs in dinuclear complexes.^68,71 A compilation of the significant Raman bands observed here, and their assignments are given in Table SI-2 (ESI†).

To quantify the spectral changes, we plot in Fig. SI-3 (ESI†) the evolution of the relative intensities of the experimental Raman shifts as a function of h. In region I (0 < h < 0.25; compare Fig. 1) one observes a decrease of the 320 cm⁻¹ (Fe–Cl) band, indicative of bound Cl⁻ being replaced by OH⁻ from solution. Such ligand exchange is corroborated by the rising 395 cm⁻¹ (Fe–OH) band intensity, accompanied by an increase of the 866 cm⁻¹ (Fe–O–Fe) band. This may be an indication of the existence of dinuclear iron species linked by oxygen. But structure details cannot be inferred from the spectra. The 188 cm⁻¹ (H₂O–H₂O, H₂O–Cl vibrations) and 1650 cm⁻¹ (H₂O) solvent band intensities are seen to stay unaffected by the iron complexation which can be explained by the much larger number of solvent molecules than iron complexes. Finally, one notices that akaganeite-related vibrations (550 cm⁻¹ and 720 cm⁻¹) are not observed in region I, exactly as expected from our conclusions drawn in Sections 3.1 and 3.2 whereupon particles occur in region II (0.25 < h < 0.5). Indeed the 395 cm⁻¹ (Fe–OH) and the 866 cm⁻¹ (Fe–O–Fe) band intensities in region II decrease, and both the 550 cm⁻¹ and 720 cm⁻¹ akaganeite signals emerge. These observations indicate the formation of larger aggregates, consistent with our qualitative conclusions drawn from the pH changes (Fig. 1). Another important observation from Fig. SI-3 (ESI†) is the intensity increase of the 320 cm⁻¹ (Fe–Cl) band, indicating that the larger oligomers arrange around Cl, which is in accord with the structure-driving nature of Cl⁻ in the formation of akaganeite. Finally, region III (0.5 < h < 1.5) reveals a simultaneous increase of the 395 cm⁻¹, 550 cm⁻¹ and 720 cm⁻¹ bands, which are the signatures of akaganeite. The constant intensities of the solvent vibrational bands (188 cm⁻¹ and 1650 cm⁻¹) in region III indicates that the properties of the solvent vibrations do not change. The Fe–Cl band (320 cm⁻¹) is seen to decrease in region III suggesting that Cl⁻ is partially expelled in later stages of the akaganeite formation, a conclusion that has been also drawn from ref. 38 as mentioned in the introduction.

3.4 SAXS measurements

To evaluate the onset of particle formation SAXS measurements were performed for 0.05 < h < 1.5. Results are shown exemplary for h = 0.25, 0.3, 0.5 and 1.0 in Fig. SI-4 (ESI†), where the scattering intensities are presented with the h = 0 scattering intensities subtracted. As can be seen, for h ≤ 0.25 (region I) only noise is being detected implying that no particles are present in the solutions; zero signal is exactly what we expect based on the pH changes and on the photoemission data. Scattering from particles sets in at h = 0.3 (mid-range region II); see the red curve in Fig. SI-4 (ESI†). This is also consistent with both our photoemission and Raman data. For larger h the scattering intensity increases. Scattering curves for the solutions, shown by the solid lines, are the best fits based on a cylinder model (compare Section 2.3). This is an appropriate assumption since akaganeite tends to form by aggregation of rod-like crystals under the present experimental conditions.¹ From the fit parameters we can determine, for each h, the radius and length of the particles. Both quantities are presented in Fig. SI-5A (ESI†) as a function of h. Note that scattering intensities for h = 0.3 are too noisy to extract a reliable length and radius. The cylindrical particles in the range of h = 0.35–1.5 (region II and III) solutions are found to have a length of 9.5–12.6 nm and radius of ∼1 nm. The increasing scattering intensities can be attributed to an increasing relative number of the particles rather than to further growth of the particles. The quantitative relation between the relative number of particles and h is shown in Fig. SI-5B (ESI†).

4. Conclusions

We have reported the very first photoelectron spectra from iron-oxo oligomers that form upon hydrolysis in iron aqueous solutions, demonstrated here for FeCl₃ (aq) with various amounts of NaOH added. The main experimental advances of the present work compared to previous X-ray studies are: (i) iron-oxo species are directly probed in aqueous solutions, for the most relevant [OH]/[Fe] ratios h = 0–0.5, using the liquid-microjet technique; (ii) valence electron binding energies have been determined, both the lowest-ionization energy of the aqueous-phase iron-oxo species, and of deeper valence energies; (iii) from a combination of non-resonant and resonant photoelectron spectroscopy, and by probing both the oxygen (1s) and the iron (2p) edges mixed iron–oxygen orbital characters are identified; (iv) X-ray absorption spectra based on partial-electron-yield detection reveal distinct absorptions of the iron-oxo oligomers, at 529 eV for O 1s, and at 709 eV for the Fe 2p resonance. An important future step would be to perform theoretical calculations of the h = 0.25 XA spectrum for several appropriately guessed oligomeric structures, and find the best match between experiment and theory. Furthermore, to narrow down the search for structures we are preparing to apply ion mobility-mass spectrometry in conjunction with soft-condition electrospray.⁷²

In addition to the electronic-structure determination of the iron-oxo oligomers we have conducted complementary Raman and SAXS measurements. We summarize our results with Fig. 4 which presents the main and most important trends, revealed from the different experimental methods; here we also include pH measurements. Our focus stays on the [OH]/[Fe] = h = 0–0.5 which covers the range where the iron-oxo oligomers are stabilized without engaging in further aggregation. One can immediately see from Fig. 4 that a given observable exhibits a discontinuous behavior at h = 0.25, which in all cases can be attributed to the occurrence of the oligomers. The photoelectron signal (B), of both oxygen and iron, exists only within a small range of h, implying that at larger OH⁻ concentrations the oligomers are consumed by aggregation. This is fully confirmed by the pH (A), Raman (C), and SAXS (D) data. Briefly, the linear behavior of pH near h = 0.25 is an indication of continuous hydrolysis and hence formation of iron-oxo oligomers. Departure from linearity is due to OH⁻ molecules reacting with H₂O molecules, and for large enough h pH trends can be explained by aggregation. The oligomer-to-particle transition is nicely corroborated by the Raman spectra which exhibit Fe–O and Fe–O–Fe bands characteristic for the small oligomers. At h > 0.25, the intensity of these bands decreases on the expense of bands typical for akaganeite. Furthermore, the exclusive existence of small oligomers, i.e., the absence of particles in the h < 0.3 solutions is confirmed by our SAXS measurements.

Fig. 4 Summary of trends from the different spectroscopic data as a function of the h = 0–0.5 (A) pH. (B) Intensities of a and b PEY-XA bands for the O 1s and the Fe 2p edges, respectively. (C) Raman lines. (D) Particle lengths and radii from SAXS measurements.

The present study demonstrates the large potential of liquid-microjet photoelectron spectroscopy for detecting the electronic structure of the initial hydrolysis products that govern subsequent nucleation and aggregation processes. Our work lays the ground for similar experiments to characterize the growth processes in other solutions, for instance Al³⁺ (aq). Equally important, we expect that the newly accessible experimental information initiates theoretical calculations, particularly of the X-ray spectra from small metal-oxo oligomers in water.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

R. S., K. K., A. K., R. K., F. E., and B. W. gratefully acknowledge financial support from the Deutsche Forschungsgemeinschaft (DFG) within the Collaborative Research Center 1109 ‘Understanding of metal oxide/water systems at the molecular scale: structural evolution, interfaces, and dissolution’. R. S. gratefully acknowledges an Emmy Noether Young Investigator stipend through the DFG (project SE 2253/3-1). R. K. is thankful for financial support from the German Cluster of Excellence in Catalysis (UNICAT) funded by the German National Science Foundation (DFG) and managed by the Technical University of Berlin (TU Berlin). The authors thank the staff at the Helmholtz-Zentrum Berlin and BESSY II for assistance during the beamtimes. Open Access funding provided by the Max Planck Society.

References

1. R. M. Cornell and U. Schwertmann, The Iron Oxides - Structure, Properties, Reactions, Occurences and Uses, Weinheim, 2003.
2. J. F. Banfield, S. A. Welch, H. Zhang, T. T. Ebert and R. L. Penn, Science, 2000, 289(5480), 751–754.
3. T. Borch, R. Kretzschmar, A. Kappler, P. V. Cappellen, M. Ginder-Vogel, A. Voegelin and K. Campbell, Environ. Sci. Technol., 2010, 44(1), 15–23.
4. S. Dixit and J. G. Hering, Environ. Sci. Technol., 2003, 37(18), 4182–4189.
5. R. Chitrakar, S. Tezuka, A. Sonoda, K. Sakane, K. Ooi and T. Hirotsu, J. Colloid Interface Sci., 2006, 298(2), 602–608.
6. A. L. Rose and T. D. Waite, Environ. Sci. Technol., 2003, 37(17), 3897–3903.
7. A. Marcu, S. Pop, F. Dumitrache, M. Mocanu, C. M. Niculite, M. Gherghiceanu, C. P. Lungu, C. Fleaca, R. Ianchis, A. Barbut, C. Grigoriu and I. Morjan, Appl. Surf. Sci., 2013, 281, 60–65.
8. M. P. Sharrock and R. E. Bodnar, J. Appl. Phys., 1985, 57(8), 3919–3924.
9. R. Dronskowski, Adv. Funct. Mater., 2001, 11(1), 27–29.
10. E. Comini, V. Guidi, C. Frigeri, I. Riccò and G. Sberveglieri, Sens. Actuators, B, 2001, 77(1–2), 16–21.
11. G. Neri, A. Bonavita, S. Galvagno, P. Siciliano and S. Capone, Sens. Actuators, B, 2002, 82(1), 40–47.
12. P. Das, B. Mondal and K. Y. Mukherjee, RSC Adv., 2014,(60), 31879.
13. A. Valdes, J. Brillet, M. Gratzel, H. Gudmundsdottir, H. A. Hansen, H. Jonsson, P. Klupfel, G.-J. Kroes, F. Le Formal, I. C. Man, R. S. Martins, J. K. Norskov, J. Rossmeisl, K. Sivula, A. Vojvodic and M. Zach, Phys. Chem. Chem. Phys., 2012, 14(1), 49–70.
14. P. Li, D. E. Miser, S. Rabiei, R. T. Yadav and M. R. Hajaligol, Appl. Catal., B, 2003, 43(2), 151–162.
15. J.-P. Jolivet, C. Chaneac and E. Tronc, Chem. Commun., 2004,(5), 481–483.
16. U. Schwertmann, J. Friedl and H. Stanjek, J. Colloid Interface Sci., 1999, 209(1), 215–223.
17. D. Gebauer, M. Kellermeier, J. D. Gale, L. Bergström and H. Cölfen, Chem. Soc. Rev., 2014, 43(7), 2348–2371.
18. H. Zhang, G. A. Waychunas and J. F. Banfield, J. Phys. Chem. B, 2015, 119(33), 10630–10642.
19. M. Zhu, C. Frandsen, A. F. Wallace, B. Legg, S. Khalid, H. Zhang, S. Mørup, J. F. Banfield and G. A. Waychunas, Geochim. Cosmochim. Acta, 2016, 172, 247–264.
20. J. Y. Bottero, A. Manceau, F. Villieras and D. Tchoubar, Langmuir, 1994, 10(1), 316–319.
21. D. Tchoubar, J. Y. Bottero, P. Quienne and M. Arnaud, Langmuir, 1991, 7(2), 398–402.
22. M. Zhu, B. Legg, H. Zhang, B. Gilbert, Y. Ren, J. F. Banfield and G. A. Waychunas, Environ. Sci. Technol., 2012, 46(15), 8140–8147.
23. J. Combes, A. Manceau and G. Calas, Geochim. Cosmochim. Acta, 1990, 54(4), 1083–1091.
24. J. M. Combes, A. Manceau, G. Calas and J. Y. Bottero, Geochim. Cosmochim. Acta, 1989, 53(3), 583–594.
25. C. M. Flynn, Chem. Rev., 1984, 84(1), 31–41.
26. W. Liu, B. Etschmann, J. Brugger, L. Spiccia, G. Foran and B. McInnes, Chem. Geol., 2006, 231(4), 326–349.
27. A. Stefánsson and T. M. Seward, Chem. Geol., 2008, 249(1), 227–235.
28. A. Kabelitz, A. Guilherme, M. Joester, U. Reinholz, M. Radtke, R. Bienert, K. Schulz, R. Schmack, R. Kraehnert and F. Emmerling, CrystEngComm, 2015, 17(44), 8463–8470.
29. J. Y. Bottero, D. Tchoubar, M. Arnaud and P. Quienne, Langmuir, 1991, 7(7), 1365–1369.
30. J. Combes, A. Manceau and G. Calas, Phys. Rev. B: Condens. Matter Mater. Phys., 1989, 158(1–3), 419–420.
31. R. N. Collins, K. M. Rosso, A. L. Rose, C. J. Glover and T. David Waite, Geochim. Cosmochim. Acta, 2016, 177, 150–169.
32. M. Zhu, B. W. Puls, C. Frandsen, J. D. Kubicki, H. Zhang and G. A. Waychunas, Inorg. Chem., 2013, 52(12), 6788–6797.
33. M. Zhu, Y. Wang, D. Meng, X. Qin and G. Diao, J. Phys. Chem. C, 2012, 116(30), 16276–16285.
34. J.-P. Jolivet, E. Tronc and C. Chanéac, C. R. Geosci., 2006, 338(6–7), 488–497.
35. J. Scheck, T. Lemke and D. Gebauer, Minerals, 2015, 5(4), 778–787.
36. J. Scheck, B. Wu, M. Drechsler, R. Rosenberg, A. E. S. Van Driessche, T. M. Stawski and D. Gebauer, J. Phys. Lett., 2016, 7(16), 3123–3130.
37. A. Manceau, Environ. Sci. Technol., 2012, 46(12), 6882–6884.
38. J. Dousma, T. Van den Hoven and P. L. De Bruyn, J. Inorg. Nucl. Chem., 1978, 40(6), 1089–1093.
39. A. Manceau and V. Drits, Clay Miner., 1993, 28, 165.
40. B. Lutz and H. Wendt, Berichte der Bunsengesellschaft für physikalische Chemie, 1970, 74(4), 372–380.
41. L. Spiccia, Inorg. Chim. Acta, 2004, 357(10), 2799–2817.
42. W. H. Casey, J. R. Rustad and L. Spiccia, Chem. – Eur. J., 2009, 15(18), 4496–4515.
43. R. Golnak, S. I. Bokarev, R. Seidel, J. Xiao, G. Grell, K. Atak, I. Unger, S. Thürmer, S. G. Aziz and O. Kühn, Sci. Rep., 2016, 6, 24659.
44. R. Seidel, S. Thürmer and B. Winter, J. Phys. Lett., 2011, 2(6), 633–641.
45. B. Winter and M. Faubel, Chem. Rev., 2006, 106(4), 1176–1211.
46. B. Winter, Nucl. Instrum. Methods Phys. Res., Sect. A, 2009, 601(1), 139–150.
47. N. Kurahashi, S. Karashima, Y. Tang, T. Horio, B. Abulimiti, Y.-I. Suzuki, Y. Ogi, M. Oura and T. Suzuki, J. Chem. Phys., 2014, 140(17), 174506.
48. B. Winter, E. F. Aziz, U. Hergenhahn, M. Faubel and I. V. Hertel, J. Chem. Phys., 2007, 126(12), 124504.
49. S. Kline, J. Appl. Crystallogr., 2006, 39(6), 895–900.
50. S. Thürmer, R. Seidel, W. Eberhardt, S. E. Bradforth and B. Winter, J. Am. Chem. Soc., 2011, 133(32), 12528–12535.
51. R. Seidel, K. Atak, S. Thürmer, E. F. Aziz and B. Winter, J. Phys. Chem. B, 2015, 119(33), 10607–10615.
52. P. Wernet, D. Nordlund, U. Bergmann, M. Cavalleri, M. Odelius, H. Ogasawara, L.-Å. Näslund, T. Hirsch, L. Ojamäe and P. Glatzel, Science, 2004, 304(5673), 995–999.
53. S. Thürmer, R. Seidel, W. Eberhardt, S. E. Bradforth and B. Winter, J. Am. Chem. Soc., 2011, 133(32), 12528–12535.
54. B. Winter, R. Weber, W. Widdra, M. Dittmar, M. Faubel and I. Hertel, J. Phys. Chem. A, 2004, 108(14), 2625–2632.
55. B. Winter, R. Weber, I. V. Hertel, M. Faubel, P. Jungwirth, E. C. Brown and S. E. Bradforth, J. Am. Chem. Soc., 2005, 127(19), 7203–7214.
56. B. Winter, M. Faubel, I. V. Hertel, C. Pettenkofer, S. E. Bradforth, B. Jagoda-Cwiklik, L. Cwiklik and P. Jungwirth, J. Am. Chem. Soc., 2006, 128(12), 3864–3865.
57. R. Seidel, B. Winter and S. E. Bradforth, Annu. Rev. Phys. Chem., 2016, 67, 283–305.
58. A. P. Gaiduk, M. Govoni, R. Seidel, J. H. Skone, B. Winter and G. Galli, J. Am. Chem. Soc., 2016, 138(22), 6912–6915.
59. R. Seidel, S. Thürmer, J. Moens, P. Geerlings, J. Blumberger and B. Winter, J. Phys. Chem. B, 2011, 115(40), 11671–11677.
60. D. Yepes, R. Seidel, B. Winter, J. Blumberger and P. Jaque, J. Phys. Chem. B, 2014, 118(24), 6850–6863.
61. S. Thürmer, M. Ončák, N. Ottosson, R. Seidel, U. Hergenhahn, S. E. Bradforth, P. Slavíček and B. Winter, Nat. Chem., 2013, 5(7), 590–596.
62. I. Hjelte, M. Piancastelli, R. Fink, O. Björneholm, M. Bässler, R. Feifel, A. Giertz, H. Wang, K. Wiesner and A. Ausmees, Chem. Phys. Lett., 2001, 334(1), 151–158.
63. R. Golnak, J. Xiao, K. Atak, I. Unger, R. Seidel, B. Winter and E. F. Aziz, J. Phys. Chem. A, 2016, 120(18), 2808–2814.
64. S. Hüfner, Photoelectron Spectroscopy: Principles and Applications, Springer-Verlag, Berlin, Heidelberg, New York, London, Paris, Tokyo, Hong Kong, Barcelona, Budapest, 1995.
65. F. De Groot and A. Kotani, Core level spectroscopy of solids, CRC press, 2008.
66. H. Kanno and J. Hiraishi, J. Raman Spectrosc., 1982, 12(3), 224–227.
67. I. Pernoll, U. Maier, R. Janoschek and G. Zundel, J. Chem. Soc., Faraday Trans. 2, 1975, 71, 201–206.
68. R. Solbrig, L. Duff, D. Shriver and I. Klotz, J. Inorg. Biochem., 1982, 17(1), 69–74.
69. S. J. Oh, D. Cook and H. Townsend, Hyperfine Interact., 1998, 112(1-4), 59–66.
70. D. M. Carey and G. M. Korenowski, J. Chem. Phys., 1998, 108(7), 2669–2675.
71. A. K. Shiemke, T. M. Loehr and J. Sanders-Loehr, J. Am. Chem. Soc., 1984, 106(17), 4951–4956.
72. J. Seo, J. Jang, S. Warnke, S. Gewinner, W. Schöllkopf and G. von Helden, J. Am. Chem. Soc., 2016, 138(50), 16315–16321.

---

Footnotes

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c7cp06945f

‡ These authors contributed equally.

---