The bond rupture force for sulfur chains calculated from quantum chemistry simulations and its relevance to the tensile strength of vulcanized rubber
Abstract
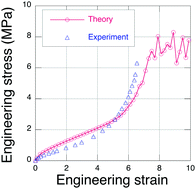
From quantum chemistry simulations using density functional theory, we obtain the total electronic energy of an eight-atom sulfur chain as its end-to-end distance is extended until S–S bond rupture occurs. We find that a sulfur chain can be extended by about 40% beyond its nominally straight conformation, where it experiences rupture at an end-to-end tension of about 1.5 nN. Using this rupture force as the chain failure limit in an explicit polymer network simulation model (EPnet), we predict the tensile failure stress for sulfur crosslinked (vulcanized) natural rubber. Quantitative agreement with published experimental data for the failure stress is obtained in these simulations if we assume that only about 30% of the sulfur chains produce viable network crosslinks. Surprisingly, we also find that the failure stress of a rubber network does not scale linearly with the chain failure force limit.


 Please wait while we load your content...
Please wait while we load your content...