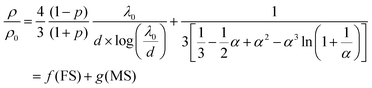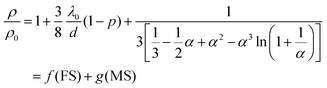Platinum for hydrogen sensing: surface and grain boundary scattering antagonistic effects in Pt@Au core–shell nanoparticle assemblies prepared using a Langmuir–Blodgett method†
K.
Rajouâ
 *,
L.
Baklouti
and
F.
Favier
*,
L.
Baklouti
and
F.
Favier
 *
*
Institut Charles Gerhardt Montpellier UMR 5253 CNRS, University of Montpellier, Campus Triolet, cc1502, 34095 Montpellier cedex 05, France. E-mail: khalil.rajoua@umontpellier.fr; frederic.favier@umontpellier.fr; Tel: +33467143332
First published on 23rd November 2017
Abstract
Hydrogen resistive sensors are fabricated through the synthesis of a series of Pt@Au core–shell nanoparticles showing various Pt shell thicknesses. Resulting colloids are assembled as hexagonal close-packed 2D monolayers of various dimension characteristics using a simple Langmuir–Blodgett method. The fabricated sensors show attractive hydrogen sensing performances with reversible responses in extended sensing ranges, a good specificity towards H2, short response and recovery times… Sensing measurements and data analyses allow the demonstration of the associated sensing mechanisms. The dissociative chemisorption of H2 and O2 on the Pt surface through a Langmuir–Hinshelwood mechanism leads to the formation of chemisorbed hydrogen and hydroxyl groups. This surface nature change induces the modification of the scattering of the conduction electrons at both the grain surface and intercontacts, tuned by the extent of hydrogen and hydroxyl group coverages. In assemblies made of particles showing thin Pt shells, the predominance of the surface scattering described by the Fuchs–Sondheimer model accounts for the observed conductive responses as the number of involved grain boundaries is limited. In contrast, in assemblies made of particles with thick Pt shells, the scattering at the grain boundaries described by the Mayadas–Shatzkes model mostly contributes to the observed resistive responses. The sensor behavior is balanced by these two antagonistic effects.
Introduction
Replacing fossil fuels as energy carriers by hydrogen is a promising alternative because of the efficient and non-polluting behaviour of hydrogen.1–3 However, hydrogen is a very explosive gas in an extended concentration range, from 4% to 75% in air. Hydrogen sensors are among the most appropriate devices to prevent associated hazards because of the odourless and tasteless characters of hydrogen. In the cycle life of hydrogen used as an energy carrier, sensors could be used at various stages:1,3,4 during production (by electrolysis, steam reforming…), storage (metal hydrides, pressurized tanks…) and conversion (fuel cells, combustion engines…). There are many kinds of hydrogen sensors:5,6 resistance based, electrochemical, catalytic, optical… Those showing the most attractive sensing performances such as the extended sensing range concentration, high sensitivity, specificity, fast response and recovery times, a small size, low power consumption, etc. are definitively resistive based sensors. They are typically composed of metal (Pd, Pt, Ag…) or semiconductors (SnO2, ZnO, WO3…) as sensing materials. However, metal-based sensors are preferred because of their specificity towards hydrogen and their low temperature of operation. The sensing layers constituted of Pd have already been extensively studied and various morphologies have been considered: films, fibres, arrays, (nano-)particles, (nano-)wires…6–16 In contrast, despite the well-known surface reactivity of Pt towards H2, reports on resistive hydrogen sensors based on Pt sensing materials remain scarce.6,12–15,17 Both Pt and Pd metals can be used for the fabrication of H2 sensors with attractive performances. However, Pd sensing layers are more versatile as their use is not restricted to oxygen containing atmospheres, in contrast with Pt based sensors. This latter point is accountable for the lower attractiveness of H2 Pt-based sensors, research-wise. On the other hand, we have recently developed an approach allowing the fabrication of well organised self-assembled arrays of Pd@Au core–shell nanoparticles.18 Gold core nanoparticles (AuNPs) were prepared using the water-based Turkevich–Frens method19,20 and decorated by a dense layer of Pd obtained by surface chemical reduction of a PdCl2 salt resulting in Pd@Au core–shell nanoparticles. The self-assembly of these core–shell particles leads to discontinuous hexagonal closed-packed monolayers showing attractive resistive H2 sensing performances. The sensing mechanism involves a balanced contribution of two electronic and mechanical antagonist effects promoted by the palladium conversion as palladium hydride under hydrogenated atmospheres. As such, the resistive electronic effect observed as the Pd metal converted as a PdHx semi-metal is counterbalanced by a conductive mechanical effect as the reversible volume increase accompanying the hydride conversion causes the closing of interparticle gaps and contacts in the 2D array.18In the present work, Pt@Au counterparts were prepared using a similar approach, for the comparison of their particulate morphologies, assembly characteristics, sensing performances and mechanisms. AuNPs were used as homogeneous seed nucleation sites for Pt nanoparticles and as building blocks for the Pt@Au core–shell nanoparticle assembly through a simple Langmuir–Blodgett method.21,22 Au cores also play the role of current collectors or nano-electrodes in the sensing layer while particle interconnections involve the Pt shell. The layers fabricated from the assembly of Pt@Au particles with various Pt shell thicknesses show attractive performances for resistive hydrogen sensing. The present paper also aims at demonstrating the drastic discrepancy in the sensing mechanism, as compared to that for Pd@Au based sensors, originating from the specificity of the reactivity of Pt towards hydrogen.18 Indeed, the dissociative chemisorption of H2 and O2 at the Pt surface following the Langmuir–Hinshelwood mechanism leads to the formation of adsorbed hydrogen and hydroxyl groups that accounts for the observed resistivity changes in the assembly. Moreover, sensing measurements are presently discussed for the demonstration of the transduction mechanism which is controlled by a combination of two antagonistic contributions originating from the modulation of the scattering of conduction electrons both at the surface and at grain boundaries upon hydrogen exposure. As the Pt thickness of the particle shell controls the number of grain boundaries involved in the layer conduction pathway, the prepared sensors show different sensing behaviours. These are modelled by a combination of the Fuchs–Sondheimer and Mayadas–Shatzkes models for a full mechanistic description.
Experimental
Gold colloid preparation
Before use, glassware was well cleaned for one hour with “aqua regia” fresh solution (3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 HCl
1 HCl![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) HNO3) followed by an additional hour of extra cleaning with “piranha solution” (7
HNO3) followed by an additional hour of extra cleaning with “piranha solution” (7![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 H2SO4
3 H2SO4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) H2O2). The glassware was then rinsed thoroughly with H2O. All solutions were prepared with distilled water (Elga H2O purification system, σ ≥ 18.2 MΩ cm−1). Gold nanoparticles were synthesized using the Turkevich–Frens's method.19,20 The typical experiment consisted of heating 50 mL of NaAuCl4, 2H2O solution (1 × 10−3 mol L−1, 99.99%, Alfa Aesar) with rapid stirring until boiling. 5 mL of sodium citrate tribasic dihydrate solution (38.8 × 10−3 mol L−1, C6H5Na3O7, 2H2O, Sigma-Aldrich) was then added. The yellow solution of NaAuCl4 became instantly transparent and then turned gradually to dark blue and to red at the end. Meanwhile, the stirring was kept for 20 min. The resulting solution was allowed to cool down to room temperature under stirring.
H2O2). The glassware was then rinsed thoroughly with H2O. All solutions were prepared with distilled water (Elga H2O purification system, σ ≥ 18.2 MΩ cm−1). Gold nanoparticles were synthesized using the Turkevich–Frens's method.19,20 The typical experiment consisted of heating 50 mL of NaAuCl4, 2H2O solution (1 × 10−3 mol L−1, 99.99%, Alfa Aesar) with rapid stirring until boiling. 5 mL of sodium citrate tribasic dihydrate solution (38.8 × 10−3 mol L−1, C6H5Na3O7, 2H2O, Sigma-Aldrich) was then added. The yellow solution of NaAuCl4 became instantly transparent and then turned gradually to dark blue and to red at the end. Meanwhile, the stirring was kept for 20 min. The resulting solution was allowed to cool down to room temperature under stirring.
Synthesis of Pt@Au core–shell nanoparticles
The Pt@Au nanoparticles were prepared using an almost identical synthetic method to that described previously.18,23–25 The initial Au colloid solution was heated and stirred to 60 °C in a water bath. 20 min later, 1.5 mL of 0.1 mol L−1 aqueous solution of L-ascorbic acid (C6H8O6, 99%, Sigma-Aldrich) freshly prepared was added to 5 mL of hot Au colloid solution under vigorous stirring. Immediately, 10 mL of an aqueous solution of dihydrogen hexachloroplatinate(IV) hexahydrate, H2PtCl6·6H2O (99.9%, Alfa Aesar) at 1.0, 5.0 or 10.0 × 10−3 mol L−1 was added to the mixture (to let the volume ratios of VAu![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) VPt reach 1
VPt reach 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2). The resulting solution had a brown colour. The stirring was extended by 20 min.
2). The resulting solution had a brown colour. The stirring was extended by 20 min.
Preparation of hydrogen sensors by interfacial assembly with the Langmuir–Blodgett technique
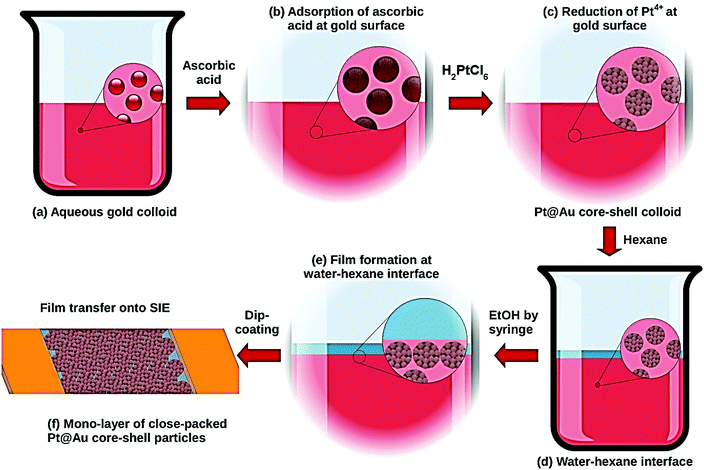
A 50 mL glass beaker was used as a simplified Langmuir–Blodgett trough for the nanoparticle assembly as shown in Fig. 1. 20 mL of Pt@Au nanoparticles were placed in a 50 mL glass beaker followed by the slow addition of 10 mL of hexane to the aqueous phase. The very slow and gentle addition with a syringe of a 5 to 10 mL volume of ethanol (p.a. 99.8%, Normapur VWR) to the aqueous phase led to the migration of the core–shell nanoparticles at the water/hexane interface and a 2D close-packed nanoparticle monolayer was gradually formed. Finally, a syringe was used to remove the excess of hexane. Glass slides with interdigitated electrodes prepared by Pt deposition through conventional photolithography techniques were used as sensor substrates allowing electrical measurements. They were cleaned in a bath of piranha solution at 100 °C and rinsed thoroughly in H2O prior to transferring the nanoparticles. The glass substrate was immersed into the aqueous phase at a certain inclined angle, and the nanoparticle monolayer was transferred by a gentle dip-coating onto the electrode side of the chip.Sensor testing
Sensing tests were carried out on fabricated sensors using a specially designed test line which allows the generation of controlled flows of various humidified hydrogenated gas mixtures in the concentration range from 0.1% to 100% of H2 in air used as a carrying gas. To prevent any interferences because of some potential cross-sensitivity toward water, the relative humidity RH is kept at 100% by bubbling the gas flow in a water vial upstream the sensor testing cell. Control measurements performed using dry gaseous mixtures did however not show any difference with those done under humidified gases. Moreover, the absence of a sensing response when using N2 as a carrying gas instead of air confirms the role of oxygen in the sensing mechanism of hydrogen by a platinum-based sensing layer. The mixing box is composed of a set of four mass-flow controllers from Bronkhorst High-Tech. Sensing measurements were performed in a Plexiglas flow cell equipped with a gas inlet and outlet, and copper cable connectors for electrical measurements. Electrical measurements were performed using a potentiostat–galvanostat PGSTAT100 from Metrohm Autolab B.V. controlled by the software General Purpose Electrochemical System GPES from Eco Chemie B.V. A 0.5 V potential bias was applied between the interdigited electrodes and consequently through the nanoparticle sensing layer. The current in the layer was recorded as a function of time. The distance between the microelectrodes was kept at 100 μm. These are made of a dense platinum layer (100 μm thick) deposited by sputtering. The resistivity of such a thick layer of platinum is not sensitive towards hydrogen.Characterisation techniques
UV-visible spectroscopy measurements were performed with a JASCO V-670 UV-VIS-NIR device using 10 mm quartz cells. Transmission electron microscopy (TEM) imaging was done using a transmission FEG JEOL 1200 EXII microscope operated at 120 kV. Sampling was carried out by depositing a drop containing the particle layer on one side of a carbon on copper grids from Agar Scientific. Scanning electron microscopy (SEM) imaging was done with a Hitachi S4800 microscope using an acceleration voltage at 15 kV. Maximum magnification was 800k at a 1 nm resolution. Samples were coated prior to imaging with a platinum layer (SC7620 Mini Sputter Coater at 30 mA for 30 s) from Quorum Technologies before imaging. The chemical composition of the films was measured using a scanning electron microscope with an energy dispersive X-ray spectrometer (SEM-EDX) Quanta FEG 200 from FEI. The temperature programmed desorption TPD measurements were performed using an Autochem 2910 device from Micromeritics.Results and discussion
2D close-packed assemblies of Pt@Au nanoparticles as sensing layers
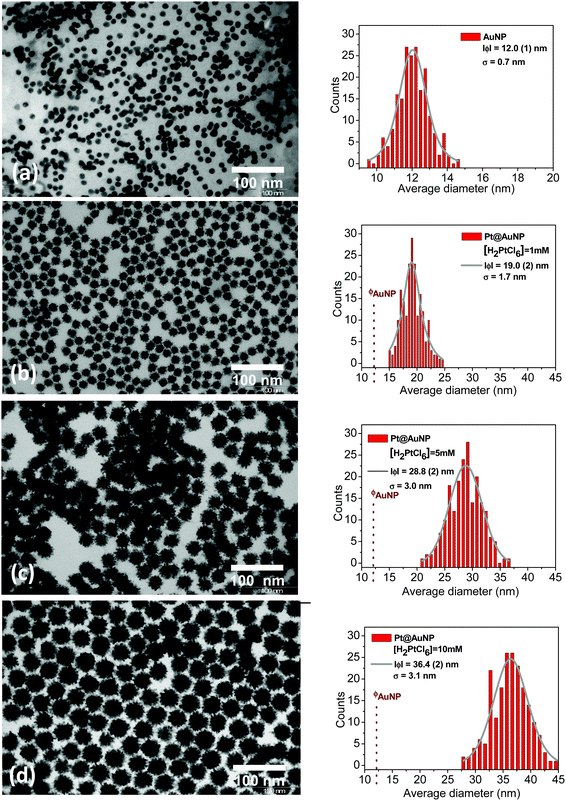
The sensing specificity toward H2 of the prepared sensors is based on the presence of a Pt shell at the surface of the Au colloids and the synthetic route presented in the present paper was developed to ensure the efficient decoration of the Au surface by Pt (Fig. 1a–c). The various steps of the Pt@Au nanoparticle synthesis were followed using UV-visible spectroscopy (Fig. S1 of the ESI†). The band at 520 nm, characteristic of the surface plasmonic resonance of gold colloids (Fig. S1, ESI† and Fig. 1a) in the visible range,26 remains after adsorption of ascorbic acid (Fig. S1, ESI† and Fig. 1b) but disappears after addition of the aqueous solution of H2PtCl6. This disappearance is a first proof of the synthesis of Pt@Au nanoparticles (Fig. S1, ESI† and Fig. 1c) since the formation of a platinum shell at the gold surface prevents the surface plasmonic resonance phenomenon. Moreover, in the spectrum of the H2PtCl6 solution (Fig. S1, ESI†), the absorption peak from the d–d transition of Pt4+, at 448 nm, is no longer observed for Pt@Au nanoparticle suspension as a proof of the complete consumption of the Pt4+ precursor salt reduced as Pt0 particles at the gold surface. As shown by TEM micrographs in Fig. 2a, the gold nanoparticles have a spherical shape with an average diameter of 12 nm. TEM was also used to evaluate the effect of the concentration of the platinum precursor on the morphology of the resulting Pt@Au core–shell nanoparticles. TEM images corresponding to the 1 mM, 5 mM and 10 mM H2PtCl6 concentrations are shown in Fig. 2b, c and d, respectively. They clearly show particles with a typical core–shell structure in which the gold core remains at a diameter of 12.0 (1) nm, whereas the diameters of the Pt@Au nanoparticles gradually increase from 19.0 (0) nm for the 1 mM H2PtCl6 precursor concentration and 28.8 (2) nm for the 5 mM precursor concentration and finally to 36.4 (2) nm for the 10 mM precursor concentration. Moreover, the particle size distributions measured over 200 individual nanoparticles for each particle set are quite narrow but were slightly broadened as the Pt precursor concentration was increased. Considering that the diameter of the gold core nanoparticles is 12.0 (1) nm, the thickness of the Pt shells can be estimated at 3.5 nm, 8.4 nm and 12.2 nm for [H2PtCl6] = 1 mM, 5 mM and 10 mM, respectively. The use of various quantities of ascorbic acid, from 0.5 mL to 6 mL keeping the same volume of the Pt precursor (10 mM) leads to Pt@Au nanoparticles with a Pt thickness shell layer close to 12 nm. It is then concluded that the Pt shell thickness depends only on the Pt precursor concentration, for a given gold colloid concentration. Moreover, TEM pictures show that the Pt growth is promoted at the surface of Au nanoparticles (i.e. no growth in solution) thanks to the efficient adsorption of the ascorbic acid at the Au surface. Unlike Pd@Au core–shell nanoparticles for which the shell is composed of a dense Pd layer,17 Pt shells are composed of small spherical nanoparticles as shown in Fig. 2 and Fig. S2, ESI.† Their average diameters were measured to be 2.5 (0.1) nm, 3.5 (0.1) nm and 3.7 (0.1) nm depending on the Pt precursor concentration at 1 mM, 5 mM and 10 mM, respectively.The core–shell particles were confirmed by XRD as composed of pure gold and platinum whatever the platinum precursor concentration at 1 mM, 5 mM and 10 mM (Fig. S3, ESI†). The corresponding diffraction peaks appear quite broad, suggesting small and/or defective crystallites. The average diameter of gold and platinum crystallites and the corresponding lattice strains were obtained using two different methods of XRD data analysis. The first one consisted in the use of the Scherrer relationship to determine the crystallite size, and the Stokes–Wilson equation for the lattice strains.27–30 The “FullProf” software was also used to extract by XRD pattern refinement the average crystallite size Lv and average maximum strain ε for each component (Pt and Au). The crystallite size Lv and the lattice strains ε calculated by the two different methods are depicted in Fig. S3e and listed in Table S1 (ESI†). The gold core crystallite size is estimated to be 11.7 (0.1) nm by Rietveld refinements, which is in good agreement with the nanoparticle size of 12.0 nm measured by TEM (Fig. 2a) confirming these as single crystals. For the platinum shells, crystallite sizes obtained from XRD data are also given in Table S1 and plotted in Fig. S3e (ESI†). They increase with the platinum precursor concentration at Lv ≈ 4, 6 and 7 nm for [H2PtCl6] at 1, 5 and 10 mM, respectively. As measured by TEM, they were found to increase in a similar way to the platinum precursor concentration but corresponding sizes are approximately half those extracted from the XRD data. This point suggests the roughly spherical platinum particles observed by TEM to be fused crystallite pairs with a limited grain boundary (similar to Janus particles or conjoined twins). Since the crystallite sizes are directly linked to the number of grain boundaries in the different sensing layers, these parameters are critical for the understanding of the sensing mechanism as discussed later in this paper.
The Pt/Au ratio in the core–shell particles was estimated in various ways, either from EDX atomic%, TEM size measurements or EDX weight% and metal densities (Table S3 and Fig. S4, ESI†). In the latter ratio, the shell is hypothetically considered as a dense layer of Pt. In all cases, the Pt/Au ratio linearly increases with the Pt precursor concentration. However, the volume ratio extracted from TEM (RTEM in Table S3 and Fig. S4, ESI†) is approximately 1.5 times larger than those from EDX measurements (REDX and RVol). Since the Au core remains, this discrepancy confirms that, as shown by TEM (Fig. 2), Pt shells are hollow volumes made of primary Pt nanoparticles.
From these observations, a few statements can be made about the growth mechanism of the platinum particles at the gold surface. First, since any unsupported Pt particles can be found by microscopy imaging, the reduction of H2PtCl6 as metallic Pt is promoted only at the surface of the gold colloids, either kinetically or thermodynamically. Second, as the Pt shell thickness varies quasi-linearly with the precursor concentration, the reducer (the ascorbic acid) in excess in the solution is dynamically adsorbed and consumed at the Au surface and subsequently, at the growing Pt surface. Finally, the particulate morphology of the Pt shells suggests that, unlike the growth of a dense Pd shell using similar conditions,18 the nucleation step is here promoted/favoured towards the growth step. Kinetics of the particle nucleation step actually depend on many parameters such as the precursor concentration, temperature, pressure, surface nature, presence of absorbents… but also on the redox potential of the cation/metal couple with respect to the reducing agent.31 In the present paper as in ref. 17 on Pd@Au, the same ascorbic acid was used as a mild reducing agent and discrepancies in the particle growth behaviour, and therefore morphology, cannot simply be explained by comparing the lower redox potential of the Pt4+/Pt0 couple at 0.758 V (vs. NHE) with that of Pd2+/Pd0 at 0.915 V.32,33 However, Pt4+ reduction to Pt0 usually proceeds in two successive steps. The first one consists in the reduction of Pt4+ to Pt2+ (the redox couple at 0.726 V). During the second step, Pt2+ is reduced as Pt0 but the redox potential is substantially greater at 1.188 V. Thermodynamically, the reduction of Pt2+ by ascorbic acid is favoured when compared to Pd2+. Similar discrepancies in the nucleation and growth of supported Pt and Pd particles have also been observed when using carbon or SiO2 substrates as deposited from the gas phase as it leads to a higher surface density of smaller Pt particles and a lower density of larger Pd particles.34 On the other hand, the narrow size distributions of the Pt@Au core–shell nanoparticles suggest a slow particle growth, certainly controlled by the diffusion of Pt2+ in the liquid state.
Different film morphologies were obtained depending on the volume of ethanol introduced during the L.B. process (Fig. S5, ESI†). For less than 5 mL of introduced EtOH, i.e. 3 mL, a grey metallic but discontinuous film is clearly visible to the naked eye at the water–hexane interface. With 5 mL (Fig. S5a, ESI†), a dense monolayer is formed with a quasi-perfect hexagonal close packed 2D arrangement of Pt@Au nanoparticles. When the added volume of ethanol reaches 7.5 mL (Fig. S5b, ESI†) and more (Fig. S5c, ESI†), resulting thick films are formed by several particle layers.
Fig. 3 shows the organisation of the Pt@Au core–shell nanoparticle assemblies organised by the Langmuir–Blodgett method. The SEM micrographs correspond to particles prepared from the platinum precursor concentration at [H2PtCl6] = 10 mM and for a volume of ethanol, VEtOH = 5 mL. Moreover, by introducing 5 mL of EtOH during the L.B. step, similar dense monolayers of close-packed and hexagonal assemblies of Pt@Au nanoparticles were obtained for Pt@Au particles with thinner shells prepared from precursor concentrations of 1 mM and 5 mM. These sensing layers were used for the sensing measurements.
Sensing measurements
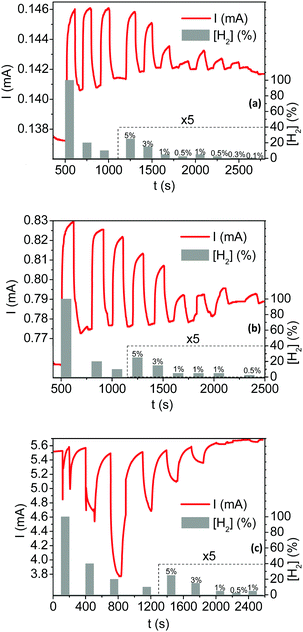
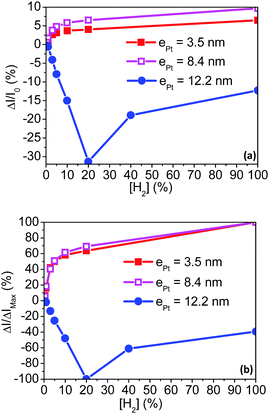
Fig. 4 depicts the current responses of the fabricated sensing layers under various hydrogenated flows, in the concentration range from 0.1% to 100% hydrogen in air. Tested sensors are successively exposed to hydrogenated atmospheres for 100 s (on state) and flushed by H2-free synthetic air for at least 200 s (off state). Switching from the on to off state promotes drastic and reversible changes in the measured current. Moreover, a clear response dependence toward the H2 concentration ([H2]) is observed over the whole sensing range. Two different types of current responses are however observed depending on the shell Pt thickness. The current increases (i.e. for a resistance decrease of the sensing layer made of Pt@Au nanoparticles) under hydrogenated gas mixtures for sensors based on the thinner Pt shells 3.5 and 8.4 nm thick (Fig. 4a and b). These responses are referred to “conductive responses” and, although not linearly, the greater the H2 concentration the larger the current amplitude. The other way around, the current decreases (i.e. the resistance of the sensitive layer increases) under hydrogenated gas mixtures using sensors based on Pt shells 12.2 nm thick (Fig. 4c): responses are then referred to “resistive responses”. For H2 concentrations below 20% in air, the greater the H2 concentration, the larger the current amplitude of these “thick shell” sensors. In contrast, for concentrations above 20%, the greater the concentration, the smaller the current response.When relative to the baseline current, the response amplitudes ΔI/I0 with I0 the current under H2-free air flow (see ESI† for calculation details) are up to five times smaller for the sensors based on thin platinum shells compared to that based on the thicker Pt shell as shown in Fig. 5a. However, the sensing range is limited for the latter sensor as it saturates at concentrations greater than 20% of H2 in air. In the whole series of fabricated sensors, the signal amplitudes are proportional to the hydrogen concentration. When depicted relative to the maximum amplitude (ΔI/IMax in Fig. 5b), the signal proportionality follows the same power law for the sensors based on the thin Pt shells (ePt = 3.5 and 8.4 nm). In contrast, for the thick Pt shell at ePt = 12.2 nm, the amplitude of the responses increases linearly with the hydrogen concentration up to 20% H2/air. These discrepancies in terms of proportionality and sensor responses either conductive or resistive demonstrate that the sensing mechanisms drastically depend on the Pt shell thickness.
The response time t90 and the recovery time trec are key technological parameters for a sensor. They correspond to the time needed for the response signal to reach 90% of the full signal amplitude at the on state and to lose 90% of the full signal amplitude at the off state, respectively. They are both depicted in Fig. S6 (ESI†) with the signal profile when exposed to a flow of 20% of hydrogen in air for the Pt@Au sensing layer with a conductive response (ePt = 8.4 nm in Fig. S6a, ESI†) and with a resistive response (ePt = 12.2 nm Fig. S6b, ESI†). Response times are measured at 50 s and 36 s for the sensors with thick and thin Pt shells, respectively. However, the recovery times are longer in both cases as they are measured at 104 s and 84 s for the sensors with thick and thin Pt shells, respectively. The effects of the operation temperature on the sensor response and recovery times have also been evaluated (Table 2 and Fig. S7, ESI†). A detailed signal analysis is given in the ESI† but, to summarize: (i) for the thin shell based sensors, the t90 response time and trec recovery time decrease with temperature. These shorter times correspond to an increase of the adsorption kinetics of H2 and/or O2 on the Pt surface; (ii) for the thick Pt shell based sensor, both the response and recovery times remain with the temperature. This discrepancy suggests that the sensing mechanism is not kinetically limited by the gas adsorption in the latter case.
Sensing mechanisms
H2 is known to chemisorb at the Pt surface in the presence of O2 through the Langmuir–Hinshelwood mechanism.35–40 This is a heterogeneous catalytic mechanism involving the dissociative adsorption of H2 and O2 to produce chemisorbed –H and hydroxyl groups –OH at the Pt surface.35–40 This catalyzed step occurs via various reactions but the route in eqn (1) is considered as dominant:37,41–44| H2(g) + 1/2O2(g) = H(ad) + OH(ad) = H2O(g) | (1) |
During the exposure of the Pt@Au based sensors under H2/O2 mixtures, the coverage rate of –H and –OH species (and H2O) depends on the hydrogen and oxygen concentrations and induces a change in the scattering of the conduction electrons at the Pt surface. Thomson was the first to correlate, back in 1901, the electrical resistivity changes with the scattering of electrons at the surface of metallic thin films.63 Later, Fuchs in 1938 and Sondheimer in 1952 established a relationship between the resistivity and the nature of the electron scattering at the metal surface of thin films.64,65 In 1969, Mayadas and Shatzkes included in the model, the electron scattering by the material defects (including grain boundaries) and bulk.66 An analogy between the Matthiessen's rule and the electronic resistivity67–72via the electron mobilities and the relaxing times allows expressing the overall variation of resistivity of a metallic thin film by the combination of the Fuchs–Sondheimer (FS) and Mayadas–Shatzkes (MS) relationships.
Depending on the film thickness (d), FS and MS combination can be written according to eqn (2) or (3):
| If d ≪ λ0 | (2) |
| If d ≫ λ0 | (3) |
with
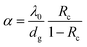 | (4) |
This combination of the Fuchs–Sondheimer and Mayadas–Shatzkes models (eqn (2) and (3)) can be used in the present case and the scattering of the conduction electrons at the surface of the Pt nanoparticles and at the inter-particle grain boundaries be considered individually to express the overall changes in resistivity during H2 sensing. As depicted in Fig. S11 (ESI†), these changes, induced by the dissociative chemisorption of H2 and O2 at the Pt surface and grain boundaries of Pt@Au particles and assembly, are expressed by p and Rc parameter values, respectively. If the sensing layers are operated under a pure air flow, the specular parameter p and the reflection coefficient Rc tend to zero, corresponding to a diffuse scattering at the surface and a total diffusion at the grain boundaries, respectively. Conversely, if the sensing layers are exposed to a hydrogen rich mixture with oxygen, p and Rc parameters tend to one, corresponding to a specular scattering and full backscattering, respectively. As shown in Fig. 4, thin Pt shell based sensing layers lead to conductive responses (Fig. 4a and b) under hydrogen exposure while thick Pt shell based sensors lead to resistive responses (Fig. 4c). Considering that the measured resistivity of the sensing layers results from these two antagonist effects, a first qualitative analysis suggests that the surface scattering contribution is dominant in the behaviour of the sensors based on thin Pt shells whereas the grain boundary contribution is dominant for thick Pt shell based sensors. More precisely, the larger the number of grain boundaries involved in the conduction path (the larger the core–shell particle size), the greater the scattering contribution directed by the M.S. model. Generally speaking, the number of grain boundaries involved impacts the balance between the F.S. and M.S. contributions to the overall resistivity. For a more quantitative analysis, the number of grain boundaries was calculated for the shortest conduction route for a 2D hexagonal arrangement of core–shell nanoparticles. It obviously depends on the particle size and dimension of the sensing layer built on the particle assembly (Fig. S12, ESI†). For thick Pt shell based sensors, the number of grain boundaries was estimated at about 24![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 700 in the shortest conduction path for an electrode span of 100 μm. Conversely, they are about 10
700 in the shortest conduction path for an electrode span of 100 μm. Conversely, they are about 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500 and 13
500 and 13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 900 grain boundaries for sensors based on thinner Pt shells, at 3.5 nm and 8.4 nm, respectively. p and Rc parameter ranges were obtained by comparing the resistivity variations measured for the fabricated sensors at various hydrogen concentrations in air with those calculated by the combination of F.S. and M.S. models from eqn (2) or (3). For these calculations, the following parameters were used: d corresponds to the thickness of the Pt shell (ePt as measured by TEM) and dg to the average diameters of the Pt crystallites (θPtNPs from XRD refinements), as given in Table 1.
900 grain boundaries for sensors based on thinner Pt shells, at 3.5 nm and 8.4 nm, respectively. p and Rc parameter ranges were obtained by comparing the resistivity variations measured for the fabricated sensors at various hydrogen concentrations in air with those calculated by the combination of F.S. and M.S. models from eqn (2) or (3). For these calculations, the following parameters were used: d corresponds to the thickness of the Pt shell (ePt as measured by TEM) and dg to the average diameters of the Pt crystallites (θPtNPs from XRD refinements), as given in Table 1.
| [H2PtCl6] (mM) | 1 | 5 | 10 |
| e Pt = d (nm) | 3.5 | 8.4 | 12.2 |
| θ PtNPs= dg (nm) | 4.3 | 6.5 | 7.9 |
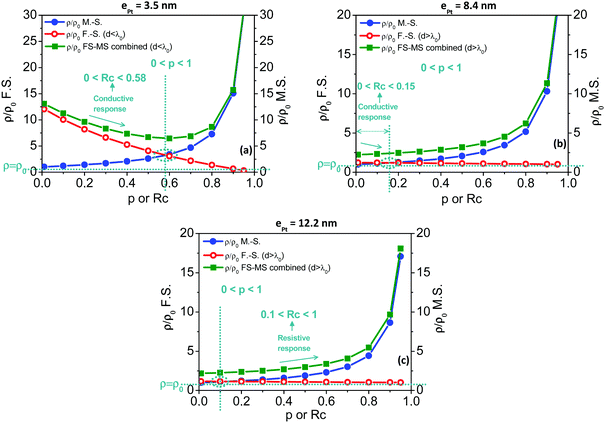
Fig. 7 depicts the resistivity changes with p or Rc as calculated using the F.S. model (red open circles), the M.S model (blue closed circles) and the combination of both F.S. and M.S. models (green closed squares). Before to comment on the resulting curves and by referring to the calculations commented in the ESI† (see Fig. S13, ESI† and corresponding comments), some specific points should be emphasized including (i) p and Rc parameters increase with the hydrogen concentration in air flows as the coverage of chemisorbed species increases, (ii) the Fuchs–Sondheimer contribution to the resistivity linearly decreases with p while the Mayadas–Shatzkes contribution hyperbolically increases with Rc, and (iii) curve portions of combined curves with negative slopes correspond to conductive sensing responses and, conversely, positive slopes to resistive responses. For the sensors based on the thinnest Pt shells at 3.5 nm, the conductive responses observed during sensing measurements under H2/O2 mixtures (Fig. 4a) can be modelled with the F.S.–M.S. combined model (Fig. 7a, green closed squares) only if Rc ranges from 0 to 0.58 since the resulting slope is positive for Rc greater than 0.58. Below Rc = 0.58, the conductive behaviour is mostly governed by the surface scattering as modelled by the F.S. model (Fig. 7a, red open circles). Meantime, the specular parameter p increases in the range 0 < p < 1 as the hydrogen concentration is increased in the gaseous mixture. The observed conductive behavior, governed by the surface scattering, is consistent with the (relatively) small number of grain boundaries in the conduction paths for this sensing nanoparticle assembly (Fig. S12, ESI†), the smallest in the series. For sensors built on particles with a 8.5 nm thick Pt shell, the resistivity behavior is depicted in Fig. 7b. The observed conductive responses under H2/air mixtures (Fig. 4b) are consistent with a resistivity behaviour mostly governed by the surface scattering, thus modelled by the F.S. model. However, the Rc parameter range for the expected negative slope is from 0 to 0.15. This expresses that, in this sensing layer, the backscattering at the grain boundaries of the conduction electrons is at most 15%. In comparison with the sensor built on particles with the thinner Pt shells, this shift towards lower Rc originates from the increase of the number of grain boundaries involved in the conduction paths as the Pt thickness increases. For the thickest Pt shells in the series (12.2 nm thick Pt shell), the resistive behaviour of the observed responses (Fig. 4c) is characterized by a positive slope of the ρ/ρ0vs. Rc curve in Fig. 7c and is mostly governed by the backscattering of the conduction electrons at the grain boundaries (M.S. model) rather than at the grain surface. This behavior is consistent only for values of the Rc coefficient reflection above 0.1. Since the sensing amplitudes are proportional to the hydrogen concentration, the reflection coefficient Rc increases in the range 0.1 < Rc < 1 as the concentration of H2 increases in the sensing atmosphere. This point is consistent with an increase of the backscattering of conduction electrons at the grain boundaries with the hydrogen concentration. From sensors of thinner to thicker Pt shells, this inversion in the contribution balance from conductive to resistive responses, from the surface governed (F.S. model) to the grain boundary governed (M.S. model), is consistent with the increase of the number of grain boundaries involved in the conduction path as the Pt shell thickness increases. The various characteristics of the fabricated sensors and calculated values for p and Rc parameters are summarized in Table 2.
| Pt@AuNPs | Thin Pt shells | Thick Pt shells | |
|---|---|---|---|
| Pt shell thickness (nm) | 3.5 | 8.4 | 12.2 |
| Sensing response | Conductive | Resistive | |
| Number of grain boundaries in conduction paths | 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 530 530 |
13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 890 890 |
24![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 730 730 |
|
t
90/[H2] = 20% T = 25 °C
t 90/[H2] = 20% T = 80 °C |
28 s
8 s |
36 s
26 s |
50 s
42 s |
|
t
rec/[H2] = 20% T = 25 °C
t rec/[H2] = 20% T = 80 °C |
42 s
10 s |
84 s
36 s |
104 s
54 s |
| Dominant contribution | Fuchs–Sondheimer | Mayadas–Shatzkes | |
| p | 0 < p < 1 | 0 < p < 1 | 0 < p < 1 |
| R c | 0 < Rc < 0.58 | 0 < Rc < 0.15 | 0.1 < Rc < 1 |
Conclusion
The synthesis of spherical Pt@Au core–shell nanoparticles is achieved with a very good control of the Pt shell thickness. Monolayers of close-packed 2D hexagonal assemblies are obtained using a Langmuir–Blodgett method and deposited on glass substrates with interdigited microelectrodes allowing hydrogen sensing measurements. Fabricated sensors show efficient sensing performances, including a good specificity towards hydrogen, high amplitude responses in the extended hydrogen concentration range from 0.1% to 100% in air, a short response and recovery times… The comprehensive study of this sensing layers based on nanoparticle assemblies allows describing and demonstrating the transduction mechanisms as occurring in two steps. A first chemical step consists in the dissociative chemisorption of H2 and O2 through the Langmuir–Hinshelwood mechanism leading to hydroxyl groups –OH and –H coverage at the Pt particle surface and grain boundaries. Then, the physical step consists in the scattering of the conduction electrons at the Pt–gas interface (either at the grain surface and boundaries). Depending on the Pt shell thickness, two kinds of sensor responses are observed. For the thinnest Pt shell based devices, the limited number of grain boundaries involved in the conduction path leads to conductive responses governed by the surface scattering as modelled by the Fuchs–Sondheimer model. Conversely, sensors based on thickest Pt shells show resistive responses. The larger number of grain boundaries involved in the conduction path leads to a sensing mechanism governed by the grain-boundary scattering, as modelled using the Mayadas–Shatzkes model.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors acknowledge the “Université de Montpellier” and “Centre National de la Recherche Scientifique” for financial support.Notes and references
- A. Züttel, A. Remhof, A. Borgschulte and O. Friedrichs, Philos. Trans. R. Soc., A, 2010, 368, 3329–3342 CrossRef PubMed.
- W. J. Buttner, M. B. Post, R. Burgess and C. Rivkin, Int. J. Hydrogen Energy, 2011, 36, 2462–2470 CrossRef CAS.
- A. Züttel, A. Borgschulte and L. Schlapbach, Hydrogen as a future energy carrier, John Wiley & Sons, 2011 Search PubMed.
- L. Schlapbach and A. Züttel, Nature, 2001, 414, 353–358 CrossRef CAS PubMed.
- V. Aroutiounian, Int. Sci. J. Altern. Energy Ecol., 2005, 23, 21–31 Search PubMed.
- T. Hübert, L. Boon-Brett, G. Black and U. Banach, Sens. Actuators, B, 2011, 157, 329–352 CrossRef.
- F. Favier, E. C. Walter, M. P. Zach, T. Benter and R. M. Penner, Science, 2001, 293, 2227–2231 CrossRef CAS PubMed.
- E. Walter, F. Favier and R. Penner, Anal. Chem., 2002, 74, 1546–1553 CrossRef CAS PubMed.
- T. Xu, M. Zach, Z. Xiao, D. Rosenmann, U. Welp, W. Kwok and G. Crabtree, Appl. Phys. Lett., 2005, 86, 203104 CrossRef.
- L. G. Villanueva, F. Fargier, T. Kiefer, M. Ramonda, J. Brugger and F. Favier, Nanoscale, 2012, 4, 1964–1967 RSC.
- C. Fournier, K. Rajoua, M.-L. Doublet and F. Favier, ACS Appl. Mater. Interfaces, 2013, 5, 310–318 CAS.
- X. Li, Y. Liu, J. C. Hemminger and R. M. Penner, ACS Nano, 2015, 9, 3215–3225 CrossRef CAS PubMed.
- K. Hassan, A. S. M. Iftekhar Uddin and G.-S. Chung, Sens. Actuators, B, 2016, 234, 435–445 CrossRef CAS.
- E. Şennik, Ş. Ürdem, M. Erkovan and N. Kılınç, Mater. Lett., 2016, 177, 104–107 CrossRef.
- A. S. M. I. Uddin, U. Yaqoob, K. Hassan and G.-S. Chung, Int. J. Hydrogen Energy, 2016, 41, 15399–15410 CrossRef CAS.
- Y. K. Mishra, G. Modi, V. Cretu, V. Postica, O. Lupan, T. Reimer, I. Paulowicz, V. Hrkac, W. Benecke and L. Kienle, ACS Appl. Mater. Interfaces, 2015, 7, 14303–14316 CAS.
- F. Yang, K. C. Donavan, S.-C. Kung and R. M. Penner, Nano Lett., 2012, 12, 2924–2930 CrossRef CAS PubMed.
- K. Rajoua, L. Baklouti and F. Favier, J. Phys. Chem. C, 2015, 119, 10130–10139 CAS.
- J. Turkevich, P. C. Stevenson and J. Hillier, Discuss. Faraday Soc., 1951, 11, 55–75 RSC.
- G. Frens, Nature, 1973, 241, 20–22 CAS.
- J. Zasadzinski, R. Viswanathan, L. Madsen, J. Garnaes and D. Schwartz, Science, 1994, 263, 1726–1738 CAS.
- I. A. Greene, F. Wu, J. Z. Zhang and S. Chen, J. Phys. Chem. B, 2003, 107, 5733–5739 CrossRef CAS.
- S. Park, P. Yang, P. Corredor and M. J. Weaver, J. Am. Chem. Soc., 2002, 124, 2428–2429 CrossRef CAS PubMed.
- L. Lu, G. Sun, H. Zhang, H. Wang, S. Xi, J. Hu, Z. Tian and R. Chen, J. Mater. Chem., 2004, 14, 1005–1009 RSC.
- J.-F. Li, Z.-L. Yang, B. Ren, G.-K. Liu, P.-P. Fang, Y.-X. Jiang, D.-Y. Wu and Z.-Q. Tian, Langmuir, 2006, 22, 10372–10379 CrossRef CAS PubMed.
- S. K. Ghosh and T. Pal, Chem. Rev., 2007, 107, 4797–4862 CrossRef CAS PubMed.
- P. Scherrer, Nachr. Ges. Wiss. Gottingen, Math.-Phys. Kl., 1918, 98–100 Search PubMed.
- A. Stokes and A. Wilson, Proc. Phys. Soc., 1944, 56, 174 CrossRef CAS.
- K. Venkateswarlu, A. Chandra Bose and N. Rameshbabu, Phys. B, 2010, 405, 4256–4261 CrossRef CAS.
- A. Monshi, M. R. Foroughi and M. R. Monshi, World J. Nanosci. Eng., 2012, 2, 154 CrossRef.
- D. V. Goia and E. Matijević, New J. Chem., 1998, 22, 1203–1215 RSC.
- M. Pourbaix, Atlas of Electrochemical Equilibria in Aqeous Solutions, 1974, 358–383 Search PubMed.
- A. J. Bard and L. R. Faulkner, Electrochemical Methods: Fundamentals and Applications, 2nd edn, 2001 Search PubMed.
- A. Schmidt, H. Eggers, K. Herwig and R. Anton, Surf. Sci., 1996, 349, 301–316 CrossRef CAS.
- I. Langmuir, J. Am. Chem. Soc., 1918, 40, 1361–1403 CrossRef CAS.
- S. Völkening, K. Bedürftig, K. Jacobi, J. Wintterlin and G. Ertl, Phys. Rev. Lett., 1999, 83, 2672 CrossRef.
- G. B. Fisher and B. A. Sexton, Phys. Rev. Lett., 1980, 44, 683 CrossRef CAS.
- R. Lewis and R. Gomer, Surf. Sci., 1969, 17, 333–345 CrossRef CAS.
- S. Tsuchiya, Y. Amenomiya and R. Cvetanović, J. Catal., 1970, 19, 245–255 CrossRef CAS.
- M. Fadoni and L. Lucarelli, Stud. Surf. Sci. Catal., 1999, 120, 177–225 CrossRef.
- B. Hellsing, B. Kasemo and V. Zhdanov, J. Catal., 1991, 132, 210–228 CrossRef CAS.
- W. Williams, C. Marks and L. Schmidt, J. Phys. Chem., 1992, 96, 5922–5931 CrossRef CAS.
- A. Michaelides and P. Hu, J. Am. Chem. Soc., 2001, 123, 4235–4242 CrossRef CAS PubMed.
- M. Matsumoto, T. Miyazaki and H. Imai, J. Phys. Chem. C, 2011, 115, 11163–11169 CAS.
- J. Freel, J. Catal., 1972, 25, 149–160 CrossRef CAS.
- G. R. Wilson and W. K. Hall, J. Catal., 1970, 17, 190–206 CrossRef CAS.
- G. R. Wilson and W. K. Hall, J. Catal., 1972, 24, 306–314 CrossRef CAS.
- J. L. Gland, G. B. Fisher and E. B. Kollin, J. Catal., 1982, 77, 263–278 CrossRef CAS.
- J. Miller, B. Meyers, F. Modica, G. Lane, M. Vaarkamp and D. Koningsberger, J. Catal., 1993, 143, 395–408 CrossRef CAS.
- A. Dedieu, Chem. Rev., 2000, 100, 543–600 CrossRef CAS PubMed.
- Y. Dong, G. Hu, X. Hu, G. Xie, J. Lu and M. Luo, J. Phys. Chem. C, 2013, 117, 12537–12543 CAS.
- W. H. Weinberg and R. P. Merrill, Surf. Sci., 1972, 33, 493–515 CrossRef CAS.
- W. H. Weinberg and R. P. Merrill, Surf. Sci., 1973, 39, 206–236 CrossRef CAS.
- W. H. Weinberg and R. P. Merrill, J. Catal., 1975, 40, 268–280 CrossRef CAS.
- D. C. Koningsberger, M. K. Oudenhuijzen, J. de Graaf, J. A. van Bokhoven and D. E. Ramaker, J. Catal., 2003, 216, 178–191 CrossRef CAS.
- M. K. Oudenhuijzen, J. A. van Bokhoven, J. T. Miller, D. E. Ramaker and D. C. Koningsberger, J. Am. Chem. Soc., 2005, 127, 1530–1540 CrossRef CAS PubMed.
- Y. Ji, V. Koot, A. M. J. van der Eerden, B. M. Weckhuysen, D. C. Koningsberger and D. E. Ramaker, J. Catal., 2007, 245, 415–427 CrossRef CAS.
- M. Keppeler and E. Roduner, Phys. Chem. Chem. Phys., 2014, 16, 26613–26616 RSC.
- N. Markovic, T. Schmidt, B. Grgur, H. Gasteiger, R. Behm and P. Ross, J. Phys. Chem. B, 1999, 103, 8568–8577 CrossRef CAS.
- H. Ogasawara, B. Brena, D. Nordlund, M. Nyberg, A. Pelmenschikov, L. Pettersson and A. Nilsson, Phys. Rev. Lett., 2002, 89, 276102 CrossRef CAS PubMed.
- D. C. Ford, Y. Xu and M. Mavrikakis, Surf. Sci., 2005, 587, 159–174 CrossRef CAS.
- L. K. Verheij, M. B. Hugenschmidt, B. Poelsema and G. Comsa, Chem. Phys. Lett., 1990, 174, 449–454 CrossRef CAS.
- J. Thomson, Proc. Cambridge Philos. Soc., 1901, 11, 120–123 Search PubMed.
- K. Fuchs, Proc. Cambridge Philos. Soc., 1938, 34, 100–108 CrossRef CAS.
- E. H. Sondheimer, Adv. Phys., 1952, 1, 1–42 CrossRef.
- A. Mayadas and M. Shatzkes, Phys. Rev. B: Solid State, 1970, 1, 1382 CrossRef.
- E. Broitman, P. Alonso and R. Zimmerman, Thin Solid Films, 1996, 277, 192–195 CrossRef CAS.
- W. Steinhögl, G. Schindler, G. Steinlesberger and M. Engelhardt, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 66, 075414 CrossRef.
- W. Steinhogl, G. Schindler, G. Steinlesberger, M. Traving and M. Engelhardt, J. Appl. Phys., 2005, 97, 023706 CrossRef.
- J. Vancea, H. Hoffmann and K. Kastner, Thin Solid Films, 1984, 121, 201–216 CrossRef CAS.
- P. Wissmann, Surf. Phys., 1975, 1–96 CAS.
- W. Steinhögl, G. Schindler, G. Steinlesberger, M. Traving and M. Engelhardt, J. Appl. Phys., 2004, 97, 023706 CrossRef.
- G. Fischer, H. Hoffmann and J. Vancea, Phys. Rev. B: Condens. Matter Mater. Phys., 1980, 22, 6065 CrossRef CAS.
Footnote |
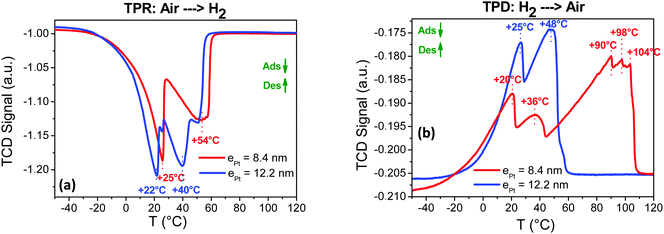
| † Electronic supplementary information (ESI) available: UV-visible spectroscopy of nanoparticle suspensions. SEM, SEM coupled EDX of the different sensing layers. XRD diffractograms and details of calculation of crystallite sizes and strains for the prepared nanoparticles. Response and recovery times and the sensing performances with the temperature for the prepared sensors. TPR and TPD of H2 with N2. Electron conduction routes in Pt@Au sensing layers and representation of the parameters p and Rc. See DOI: 10.1039/c7cp06645g |
| This journal is © the Owner Societies 2018 |