Nonadiabatic rotational states of the hydrogen molecule
Received
22nd September 2017
, Accepted 24th November 2017
First published on 24th November 2017
Abstract
We present a new computational method for the determination of energy levels in four-particle systems like H2, HD, and HeH+ using explicitly correlated exponential basis functions and analytic integration formulas. In solving the Schrödinger equation, no adiabatic separation of the nuclear and electronic degrees of freedom is introduced. We provide formulas for the coupling between the rotational and electronic angular momenta, which enable calculations of arbitrary rotationally excited energy levels. To illustrate the high numerical efficiency of the method, we present the results for various states of the hydrogen molecule. The relative accuracy to which we determined the nonrelativistic energy reached the level of 10−12–10−13, which corresponds to an uncertainty of 10−7–10−8 cm−1.
1 Introduction
The hydrogen molecule gives an opportunity to test the foundations of quantum chemistry, which are based on quantum electrodynamic theory. In principle, there are no limits to the theoretical precision of the determination of molecular levels, apart from the limited accuracy of fundamental constants, such as the electron-proton mass ratio, the Rydberg constant, or the nuclear mean square charge radii. This opens up the possibility to determine these fundamental constants from molecular spectroscopic data, or alternatively to look for any discrepancies between theoretical predictions and experimental results to search for as yet unknown interactions.1 In fact, in recent years we have observed significant progress in the accuracy of molecular spectroscopy.2–10 In the particular case of the hydrogen molecule, contemporary measurements have reached the accuracy of 10−5 cm−1 (relative 10−9) for selected transitions.11–13 On the theoretical side, various relativistic and quantum electrodynamic corrections have recently been calculated,14,15 but the principal problem up to now has been the insufficient accuracy of nonrelativistic energy levels. In a general multiparticle case, the complexity of the Schrödinger equation prevents its accurate solution and enforces approximations to be made. The most common one is the adiabatic approximation, which assumes the separation of the electronic and nuclear dynamics. Only a few attempts to solve directly, i.e. without the adiabatic approximation, the four-body Schrödinger equation for H2 have been published. The first successful method was developed by Kołos and Wolniewicz over 50 years ago.16,17 They employed a nonadiabatic expansion of a trial wave function in products of electronic James–Coolidge basis functions18 and the vibrational functions of the form hn(R) = R−3e−x2/2![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) n(x) with x = β|R − Re|, where β and Re are variational parameters, and
n(x) with x = β|R − Re|, where β and Re are variational parameters, and ![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) n denotes the n-th Hermite polynomial. The expansion was composed of 54 electronic terms and six hn functions yielding 147-terms in total. Because of this relatively short expansion, the obtained nonrelativistic dissociation energy D0 = 36114.7 cm−1 differed by ca. 3 cm−1 from the exact value. Nevertheless, the pioneering work by Kołos and Wolniewicz has set the foundations of the theoretical techniques for accurate calculations and, regarding the then available computing capabilities, should be considered as a great success of theory. Fifteen years later, using the same type of wave functions with significantly larger (1070-term) and carefully optimized expansion, a refined integration method, and much more powerful computers, Bishop and Cheung19 reduced the error to 0.2 cm−1. Quite a different approach, based on the quantum Monte Carlo method, was presented by Traynor et al.20 in 1991 and improved later by Chen and Anderson.21 Their trial wave function was a product of four terms ψi. The first two terms were a combination of one-electron functions centered on nuclei A and B, ψi = e−ariA + e−ariB. The third term was the Jastrow factor responsible for interparticle correlation and cusps
n denotes the n-th Hermite polynomial. The expansion was composed of 54 electronic terms and six hn functions yielding 147-terms in total. Because of this relatively short expansion, the obtained nonrelativistic dissociation energy D0 = 36114.7 cm−1 differed by ca. 3 cm−1 from the exact value. Nevertheless, the pioneering work by Kołos and Wolniewicz has set the foundations of the theoretical techniques for accurate calculations and, regarding the then available computing capabilities, should be considered as a great success of theory. Fifteen years later, using the same type of wave functions with significantly larger (1070-term) and carefully optimized expansion, a refined integration method, and much more powerful computers, Bishop and Cheung19 reduced the error to 0.2 cm−1. Quite a different approach, based on the quantum Monte Carlo method, was presented by Traynor et al.20 in 1991 and improved later by Chen and Anderson.21 Their trial wave function was a product of four terms ψi. The first two terms were a combination of one-electron functions centered on nuclei A and B, ψi = e−ariA + e−ariB. The third term was the Jastrow factor responsible for interparticle correlation and cusps 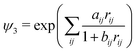 and the last term accounted for nuclear vibration and was of the Gaussian form ψ4 = e−d(R−c)2. The quantum Monte Carlo method allowed the finite basis set error to be eliminated but introduced instead a statistical (sampling) error, which in the latter calculations was of about ±0.2 cm−1. A breakthrough result has been published by Kinghorn and Adamowicz.22,23 Using a 512-term basis of explicitly correlated Gaussian functions, they have diminished the error in the nonrelativistic D0 to 1.7 × 10−3 cm−1. Later on, successively improving the optimization technique and expanding the basis set size to 10
and the last term accounted for nuclear vibration and was of the Gaussian form ψ4 = e−d(R−c)2. The quantum Monte Carlo method allowed the finite basis set error to be eliminated but introduced instead a statistical (sampling) error, which in the latter calculations was of about ±0.2 cm−1. A breakthrough result has been published by Kinghorn and Adamowicz.22,23 Using a 512-term basis of explicitly correlated Gaussian functions, they have diminished the error in the nonrelativistic D0 to 1.7 × 10−3 cm−1. Later on, successively improving the optimization technique and expanding the basis set size to 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 terms, Bubin and Adamowicz24–26 arrived at an extremely accurate solution of the four-particle Schrödinger equation to obtain D0 = 36118.79774(1)cm−1.
000 terms, Bubin and Adamowicz24–26 arrived at an extremely accurate solution of the four-particle Schrödinger equation to obtain D0 = 36118.79774(1)cm−1.
All these calculations have been limited to the nonrotational state of the molecule (J = 0). In this work, we show how to incorporate the coupling between the rotational and electronic angular momentum in a straightforward manner and increase the accuracy of the nonrelativistic dissociation energy up to the level of 10−7–10−8 cm−1 for the ground as well as for the rotationally and vibrationally excited energy levels of the electronic X1Σ+g state. This project comprises one of the stages heading toward the prediction of the total energies of the hydrogen molecule with the accuracy of 10−6 cm−1. The other contributions are relativistic O(α2), leading quantum electrodynamics O(α3), and higher order O(α4) which are known only within the adiabatic approximation.15 The knowledge of nonadiabatic wave functions obtained here, is essential for the calculation of these contributions.
2 Method
2.1 From a general exponential to the nonadiabatic James–Coolidge basis function
The method described here is relevant to a molecule consisting of two electrons, labeled 1 and 2, and two nuclei, labeled A and B, with masses MA and MB and charges ZA and ZB. The nonrelativistic Hamiltonian for this system is| | 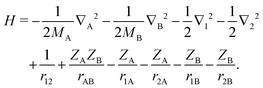 | (1) |
We start the description of the method with a general exponential basis function of the following translationally invariant form
| | 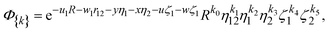 | (2) |
where
u1,
w1,
y,
x,
u, and
w are real numbers, whereas
ki are nonnegative integers, and where
| | 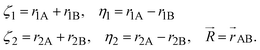 | (3) |
By setting u1 ≡ α, w1 = 0, y = 0, x = 0, and u = w = β we arrive at simplified basis functions
| | 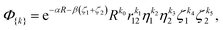 | (4) |
which still form a complete basis set. We call this function the nonadiabatic James–Coolidge (naJC) function due to its resemblance to the original James–Coolidge (JC) basis function used in fixed-nuclei calculations. The difference between our nonadiabatic function and the JC function is in the internuclear correlation factor as well as in the meaning of the
ζ and
η variables.
2.2 The variational nonadiabatic wave function for an arbitrary rotational angular momentum
The rotational angular momentum of nuclei couples to the electronic angular momentum, ![[L with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_004c_20d1.gif) , and gives the total angular momentum
, and gives the total angular momentum ![[J with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_004a_20d1.gif) of a molecule. For this reason, the wave function ΨJ,M of a rotational level J (formally depending also on the projection of
of a molecule. For this reason, the wave function ΨJ,M of a rotational level J (formally depending also on the projection of ![[J with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_004a_20d1.gif) on the Z axis in the laboratory frame) must contain components that describe the electronic Σ, Π, and Δ,… states. In the following set of formulas we construct such a wave function and we introduce a necessary notation. The total wave function is a sum of the components with growing Λ—the eigenvalue of the
on the Z axis in the laboratory frame) must contain components that describe the electronic Σ, Π, and Δ,… states. In the following set of formulas we construct such a wave function and we introduce a necessary notation. The total wave function is a sum of the components with growing Λ—the eigenvalue of the ![[n with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006e_20d1.gif) ·
·![[L with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_004c_20d1.gif) operator
operator| | | ΨJ,M = ΨJ,MΣ + ΨJ,MΠ + ΨJ,MΔ+… | (5) |
where| | ΨJ,MΣ = YJMΦJΣ, for ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) J ≥ 0 J ≥ 0 | (6) |
| | 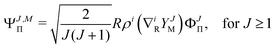 | (7) |
| | 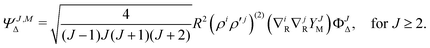 | (8) |
The particular form of functions in eqn (6)–(8) is convenient for the calculation of matrix elements as for example, the overlap matrix is block diagonal. In the above equations we use the following notation
| | 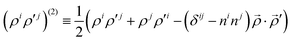 | (9) |
| | 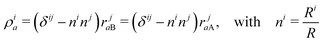 | (11) |
and we assume the Einstein summation convention,
i.e. an implicit sum over all values of a repeated Cartesian index. The symbol
YJM =
YJM(
![[n with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006e_20d1.gif)
) denotes the spherical harmonic. The functions
ΦJΛ represent linear expansions in the above-defined naJC basis functions
(4)| | 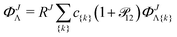 | (12) |
for Λ = Σ, Π, Δ,…. For each pair
J and Λ, the function
ΦJΛ has its own set of nonlinear parameters, therefore we distinguish
Φ{k} of
eqn (4) by indices
J and Λ. In the equation above, the symbol
![[scr P, script letter P]](https://www.rsc.org/images/entities/char_e52f.gif) 12
12 means the electron permutation operator and the linear coefficients
c{k} are determined variationally.
The nuclear rotation in the wave function ΨJ,M is described by the spherical harmonics YJM(![[n with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006e_20d1.gif) ), whereas the electronic angular contribution is represented in the form of the expansion (5) in Cartesian coordinates ρi. Each term of this expansion represents a function with a well-defined projection of the electronic angular momentum Λ. Moreover, the product of
), whereas the electronic angular contribution is represented in the form of the expansion (5) in Cartesian coordinates ρi. Each term of this expansion represents a function with a well-defined projection of the electronic angular momentum Λ. Moreover, the product of 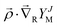 commutes with the total angular momentum operator
commutes with the total angular momentum operator ![[J with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_004a_20d1.gif) so that it preserves the correct J and M quantum numbers. Finally, this expansion is complete. In practice, though, it can be cut due to the rapidly decreasing contribution from the subsequent terms.
so that it preserves the correct J and M quantum numbers. Finally, this expansion is complete. In practice, though, it can be cut due to the rapidly decreasing contribution from the subsequent terms.
A note concerning a linear dependence and a completeness of the basis set is in place here. To ensure the completeness, the function ΨJ,MΔ appears in two variants. The one in which both ρ and ρ′ point at the same electron, and the other, in which they point at different electrons. Certain combinations of these two variants are linearly dependent, which originates from the following identity
| | 2![[small rho, Greek, vector]](https://www.rsc.org/images/entities/i_char_e137.gif) 1 1![[small rho, Greek, vector]](https://www.rsc.org/images/entities/i_char_e137.gif) 2(ρi1ρj2)(2) = 2(ρi1ρj2)(2) = ![[small rho, Greek, vector]](https://www.rsc.org/images/entities/i_char_e137.gif) 22(ρi1ρj1)(2) + 22(ρi1ρj1)(2) + ![[small rho, Greek, vector]](https://www.rsc.org/images/entities/i_char_e137.gif) 12(ρi2ρj2)(2). 12(ρi2ρj2)(2). | (13) |
This linear dependence can be avoided by, for example, using the second variant basis functions with at least one
ki = 0, for
i = 2,…,5.
2.3 Symmetry of the wave function
The nonrelativistic Hamiltonian (1) is invariant under translation, rotation, and spatial inversion ![[P with combining circumflex]](https://www.rsc.org/images/entities/i_char_0050_0302.gif) . The inversion
. The inversion ![[P with combining circumflex]](https://www.rsc.org/images/entities/i_char_0050_0302.gif) reverses the sign of spatial coordinates of all particles leaving their spin unchanged, and the wave function is an eigenstate of
reverses the sign of spatial coordinates of all particles leaving their spin unchanged, and the wave function is an eigenstate of ![[P with combining circumflex]](https://www.rsc.org/images/entities/i_char_0050_0302.gif) with eigenvalues ±1. The wave function has also a definite symmetry with respect to the exchange of electrons—it is either symmetric or antisymmetric for the total electronic spin S = 0 or 1, respectively. In practice, this symmetry is enforced by acting on the spatial wave function with the
with eigenvalues ±1. The wave function has also a definite symmetry with respect to the exchange of electrons—it is either symmetric or antisymmetric for the total electronic spin S = 0 or 1, respectively. In practice, this symmetry is enforced by acting on the spatial wave function with the 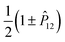 operator, where
operator, where ![[P with combining circumflex]](https://www.rsc.org/images/entities/i_char_0050_0302.gif) 12 exchanges the electron labels.
12 exchanges the electron labels.
For a homonuclear molecule, additional symmetries arise. The gerade/ungerade inversion symmetry is the inversion of all electronic coordinates with respect to the geometric center of a molecule. Recalling how the inversion operator î acts on the electronic variables îζi = ζi, îηi = −ηi, and îr12 = r12, one finds that îΦ{k}= (−1)k2+k3Φ{k} and hence
| | 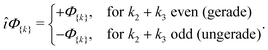 | (14) |
A wave function of a homonuclear molecule also has a symmetry due to the exchange of the nuclei. For a specified gerade/ungerade inversion symmetry and the total nuclear spin, only even or odd J levels are allowed depending on the statistics (boson or fermion) of the nuclei. For example, if we restrict our considerations to the electronic ground state (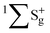 ) of H2, we observe that the subsequent rotational levels assume alternate nuclear spins. As a result, the even J levels correspond to the nuclear singlet (para-hydrogen) and the odd J levels to the triplet state (ortho-hydrogen).
) of H2, we observe that the subsequent rotational levels assume alternate nuclear spins. As a result, the even J levels correspond to the nuclear singlet (para-hydrogen) and the odd J levels to the triplet state (ortho-hydrogen).
2.4 Reduction of the angular factor
An important step in the analytic evaluation of the matrix elements with functions ΨJ,MΛ is the integration over the nuclear angular variables. In this section, we supply formulas for the reduction of the general matrix elements by performing the integration 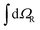 . Let us first note, that for an arbitrary scalar operator Q we have
. Let us first note, that for an arbitrary scalar operator Q we have 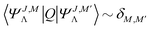 . In the simplest case of matrix elements with a scalar electronic (i.e. containing no differentiation over R) operator Qel we have
. In the simplest case of matrix elements with a scalar electronic (i.e. containing no differentiation over R) operator Qel we have| | | 〈ΨJ,MΣ|Qel|ΨJ,MΣ〉 = 〈ΦJΣ|Qel|ΦJΣ〉 | (15) |
| | | 〈ΨJ,MΠ|Qel|ΨJ,MΠ〉 = 〈ρiΦJΠ|Qel|ρiΦJΠ〉 | (16) |
| | | 〈ΨJ,MΔ|Qel|ΨJ,MΔ〉 = 〈(ρiρ′j)(2)ΦJΔ|Qel|(ρiρ′j)(2)ΦJΔ〉 | (17) |
and all the off-diagonal matrix elements vanish. The next set of formulas applies to the diagonal matrix elements with the nuclear kinetic energy operator| | 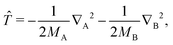 | (18) |
namely| | | 〈ΨJ,MΣ|∇X2|ΨJ,MΣ〉 = 〈ΦJΣ|∇X2 − J(J + 1)R−2|ΦJΣ〉 | (19) |
| | | 〈ΨJ,MΠ|∇X2|ΨJ,MΠ〉 = 〈ρiΦJΠ|∇X2 − [J(J + 1) − 2]R−2|ρiΦJΠ〉 | (20) |
| | | 〈ΨJ,MΔ|∇X2|ΨJ,MΔ〉 = 〈(ρiρ′j)(2)ΦJΔ|∇X2 − [J(J + 1) − 6]R−2|(ρiρ′j)(2)ΦJΔ〉 | (21) |
with X = A or B. Finally, the nondiagonal matrix elements read| | 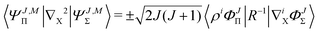 | (22) |
| | 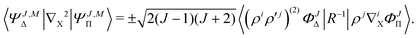 | (23) |
where + and − is for X = A and B, correspondingly, with ![[R with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0052_20d1.gif) =
= ![[R with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0052_20d1.gif) A −
A − ![[R with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0052_20d1.gif) B. All the remaining matrix elements vanish, so that the overlap and Hamiltonian matrices have the following block-band structure
B. All the remaining matrix elements vanish, so that the overlap and Hamiltonian matrices have the following block-band structure| | 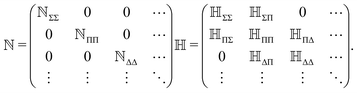 | (24) |
2.5 Integrals with the exponential function
The previous section dealt with matrix elements without any reference to a specific shape of the spatial part of the basis function. Therefore, the above formulas can be utilized also with types of basis functions other than that presented in this article, e.g. with explicitly correlated Gaussian functions.26 The present section, in turn, is devoted to the exponential basis functions, in particular to the naJC functions of eqn (4). We start, however, with the most general integral for a four-body system| | 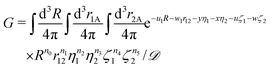 | (25) |
where| | 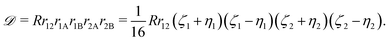 | (26) |
The matrix elements of the Hamiltonian evaluated in the exponential basis (2) can be expressed by a combination of integrals belonging to the class defined in eqn (25). All of these integrals can be obtained through a recurrence relation starting from the so called master integral| | 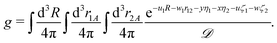 | (27) |
The analytical form of the integral (27) was obtained by Fromm and Hill27 in 1987. Their result, although terribly troublesome for a numerical evaluation, was a milestone in the evaluation of the four-body exponential integrals. A special case of this integral was evaluated analytically by Remiddi,28 who expressed his result in terms of the logarithmic and the Euler dilogarithmic functions. In 1997 a significant simplification of the result obtained by Fromm and Hill was achieved by Harris,29 who managed to eliminate the original singularities and arrive at a much more computationally friendly formulation. Another significant step in this field was made in 2009 when the effective recurrence relations were discovered30 enabling evaluation of an arbitrary integral out of the whole class given by eqn (25).
The master integral g and its derivatives satisfy the following differential equations30
| | 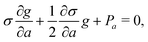 | (28) |
where
a is one of the parameters
u1 ≡
t,
w1,
y,
x,
u, or
w, and where
| | | σ = σ0 + t2σ2 + t4σ4, | (29) |
| σ0 = w12(u + w − x − y)(u − w + x − y)(u − w − x + y)(u + w + x + y) + 16(wx − uy)(ux − wy)(uw − xy), |
| σ2 = w14 − 2w12(u2 + w2 + x2 + y2) + 16uwxy, |
The inhomogeneous term Pa is a combination of several logarithmic functions and is presented explicitly in Appendix A of ref. 31.
The most general integral of eqn (25) can be obtained by successive, multiple differentiation of the master integral g
| | 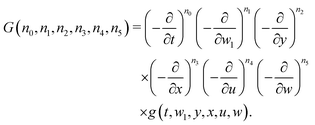 | (30) |
Each differentiation increases by one the power of the associated variable in the pre-exponential factor of the integrand in
eqn (27). However, from the practical point of view, it is much more convenient to use recursion relations for increasing the powers
ni. Let us briefly overview the steps leading to these recurrence relations. First, in
eqn (28) we set
a =
y and generate the pertinent inhomogeneous term
Py. Next, we differentiate
Eqn (28)n2 times with respect to
y and then set
y = 0. We proceed analogously with the variables
x and
w1, and obtain the relation connecting different integrals of the
G-class. From this equation we extract
G(
n0,
n1,
n2,
n3,
n4,
n5) and obtain the recurrence relation which, starting from
G(0,0,0,0,0,0), enables the integrals
G to be obtained for an arbitrary combination of non-negative integers
ni, expressed in terms of derivatives of
Py. The multiple derivatives of
Py are combinations of rational and logarithmic functions, and are numerically stable for
t − 2
u sufficiently far from zero. This condition can be easily satisfied and does not introduce limitations in practical calculations. Setting
w1,
y, and
x to zero simplifies significantly the analytic expressions for integrals in the naJC basis; in particular the
σ from
eqn (29) vanishes.
A small sample of explicit expressions for G and Py is given below (for w = u). Note that the master integral (27) for the naJC basis is represented explicitly by G(0,0,0,0,0,0).
| | | G(0,0,0,0,0,0) = Py(0,0,1,0,0,0)/(16u4) | (31) |
| | | G(0,0,0,0,0,1) =Py(0,0,1,0,0,0)/(8u5) + Py(0,0,1,0,0,1)/(16u4) | (32) |
| | | G(0,0,0,0,1,0) = G(0,0,0,0,0,1) | (33) |
| | | G(0,1,0,0,0,0) = Py(0,1,1,0,0,0)/(16u4) | (36) |
where
| | 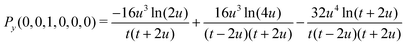 | (37) |
| | 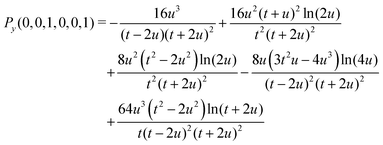 | (38) |
| | 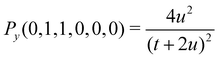 | (39) |
We note that, by symmetry, the integrals G with n2 + n3 odd vanish, as do Py with n2 + n3 even. The procedure sketched above allows the whole G-class of integrals to be evaluated analytically in a simple form.
3 Numerical approach
3.1 A perturbative solution of the eigenvalue problem
The solution of the Schrödinger equation in terms of the basis functions (4) is now reformulated into the generalized eigenvalue problem with the Hamiltonian ![[Doublestruck H]](https://www.rsc.org/images/entities/char_e16b.gif) and overlap
and overlap ![[Doublestruck N]](https://www.rsc.org/images/entities/char_e171.gif) matriceswhere
matriceswhere ![[Doublestruck C]](https://www.rsc.org/images/entities/char_e166.gif) is a vector of linear coefficients from eqn (12). For all states this equation can be solved directly, e.g. by the inverse iteration method. However, due to the large size of the matrices
is a vector of linear coefficients from eqn (12). For all states this equation can be solved directly, e.g. by the inverse iteration method. However, due to the large size of the matrices ![[Doublestruck H]](https://www.rsc.org/images/entities/char_e16b.gif) and
and ![[Doublestruck N]](https://www.rsc.org/images/entities/char_e171.gif) for rotational states, it is more economical to apply the inverse iteration method only for the Σ component, and obtain the Π and Δ components from the standard perturbation theory. In other words, when J > 0, the wavefunction ΨJ,M, as defined in Section 2.2, is composed of mutually orthogonal Λ-segments. The orthogonality is manifested in the block-diagonal structure of the overlap matrix, eqn (24). The small block-off-diagonal terms of matrix
for rotational states, it is more economical to apply the inverse iteration method only for the Σ component, and obtain the Π and Δ components from the standard perturbation theory. In other words, when J > 0, the wavefunction ΨJ,M, as defined in Section 2.2, is composed of mutually orthogonal Λ-segments. The orthogonality is manifested in the block-diagonal structure of the overlap matrix, eqn (24). The small block-off-diagonal terms of matrix ![[Doublestruck H]](https://www.rsc.org/images/entities/char_e16b.gif) enable rapidly converging perturbative expansion. In this section, we supply explicit formulas for the subsequent perturbational corrections.
enable rapidly converging perturbative expansion. In this section, we supply explicit formulas for the subsequent perturbational corrections.
Let us first consider the approximated energy level E(0) = EΣ obtained from the unperturbed wavefunction ΨJ,M = ΨJ,MΣ. The Rayleigh–Schrödinger perturbation theory yields the second order (with respect to the power of the off-diagonal parts of the Hamiltonian) energy shift E(2)Π
| | 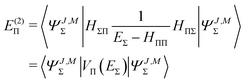 | (41) |
where
| | 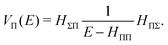 | (42) |
The fourth order correction E(4)Π + E(4)Δ can be evaluated from
| | 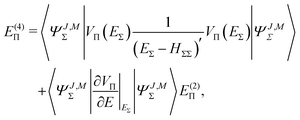 | (43) |
| | 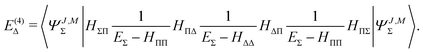 | (44) |
Each HΛ′Λ Hamiltonian contains the m/μ factor of the order of 10−3, which makes the perturbation series converge very rapidly. In particular, the E(6)Δ correction would be approximately 5–6 orders of magnitude smaller than E(4)Δ. Therefore, taking into account just the first four terms of the perturbative expansion is sufficient for our purposes
| | | E ≈ EΣ + E(2)Π + E(4)Π + E(4)Δ. | (45) |
A similar perturbation expansion holds for the wave function, namely
| | 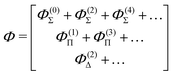 | (46) |
where
| | | Φ(0)Σ is the unperturbed function | (47) |
| | 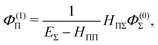 | (48) |
| | 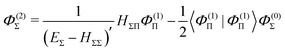 | (49) |
| | 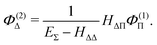 | (50) |
3.2 Technical details
Each naJC basis function Φ{k}, apart from the set of integers ki, depends on two real positive parameters αk and βk. The set of the basis functions with a common pair αk and βk will be called the sector. Such a sector contains all basis functions with integer powers of R ranging from kmin0 to kmax0. The total wave function can be composed of a number of such sectors. The optimal value kmax0 was determined through numerical experiments for each state separately. The kmin0 in turn was set to Λ. The ‘electronic’ integer parameters k1…,k5 are used to organize the basis functions in ‘shells’. The given basis function Φ{k} belongs to the shell number 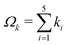 . To describe a sector of basis functions for given J and Λ values, we use a four parameter symbol (kmax0,Ω,α,β). Such a sector involves basis functions with the nonlinear parameters α and β, and with the integer powers ki fulfilling kmin0 ≤ k0 ≤ kmax0 and 0 ≤ Ωk ≤ Ω. By increasing Ω we can systematically add new basis functions to the expansion and observe the convergence of energy with an increasing total size of the basis set K.
. To describe a sector of basis functions for given J and Λ values, we use a four parameter symbol (kmax0,Ω,α,β). Such a sector involves basis functions with the nonlinear parameters α and β, and with the integer powers ki fulfilling kmin0 ≤ k0 ≤ kmax0 and 0 ≤ Ωk ≤ Ω. By increasing Ω we can systematically add new basis functions to the expansion and observe the convergence of energy with an increasing total size of the basis set K.
To solve the eigenproblem (41) we employed the inverse iteration method, which consists of the ![[Doublestruck M]](https://www.rsc.org/images/entities/char_e170.gif)
![[Doublestruck D]](https://www.rsc.org/images/entities/char_e167.gif)
![[Doublestruck M]](https://www.rsc.org/images/entities/char_e170.gif) T decomposition of the
T decomposition of the ![[Doublestruck H]](https://www.rsc.org/images/entities/char_e16b.gif) − E
− E![[Doublestruck N]](https://www.rsc.org/images/entities/char_e171.gif) matrix followed by a solution of the linear equations set performed several times up to the assumed convergence. The matrix
matrix followed by a solution of the linear equations set performed several times up to the assumed convergence. The matrix ![[Doublestruck D]](https://www.rsc.org/images/entities/char_e167.gif) is block diagonal with blocks of the order 1 or 2, and
is block diagonal with blocks of the order 1 or 2, and ![[Doublestruck M]](https://www.rsc.org/images/entities/char_e170.gif) is unit lower triangular. The workload of the decomposition step grows with the basis size like K3 whereas that of the remainder steps like K2; therefore, for large matrices the decomposition step determines the timing of all of the computations. The linear algebra calculations, as well as the evaluation of matrix elements, were performed using extended precision arithmetics implemented with the help of the QD library.32 It enables nearly octuple precision (212 bit, 62 digits), which is sufficient to obtain the required accuracy of the energy levels considered in this work.
is unit lower triangular. The workload of the decomposition step grows with the basis size like K3 whereas that of the remainder steps like K2; therefore, for large matrices the decomposition step determines the timing of all of the computations. The linear algebra calculations, as well as the evaluation of matrix elements, were performed using extended precision arithmetics implemented with the help of the QD library.32 It enables nearly octuple precision (212 bit, 62 digits), which is sufficient to obtain the required accuracy of the energy levels considered in this work.
We consider H2 in its electronic ground state X1Σ+g and, due to limited space for tables, we restrict the presentation of numerical results to the ground vibrational level v = 0. This restriction, however, is not related to limitations of the method.
3.3
J = 0 level
We consider here the ground rotational level J = 0, which requires no coupling to the electronic states with higher angular momentum to be involved, that is ΨJ,M = ΨJ,MΣ. We used a two-sector basis of Σ-functions: (30,Ω,α,β(1)) and (30,Ω-2,α,β(2)). The parameters α, β(1), and β(2) were optimized variationally with respect to the energy of the level separately for each Ω. The optimal parameters, the total size of the basis, and the resulting energy are listed in Table 1. Extrapolation of the energy to an infinite basis set size enables determination of the recommended energy value and its estimated numerical uncertainty. For this particular level, we assess the accuracy of the energy as 3 × 10−13 hartree. By subtracting the energy E0,0 from the exactly known sum of the energy of two hydrogen atoms, 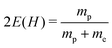 hartree, we calculated the dissociation energy D0,0 listed in the last column of the table. The numerical accuracy of D0,0 is estimated to be 3 × 10−8 cm−1. This estimation, however, does not account for the uncertainty originating from determination of the fundamental physical constants. All calculations reported in this work were performed with the best currently available values of the proton-to-electron mass ratio mp/me = 1836.15267389(17) and of the Rydberg constant R∞ = 109737.31568508(65) cm−1 obtained from the 2014 CODATA compilation.33 The uncertainties of both physical constants limit the accuracy of our final results. On the other hand, the problem can be reversed and future high-accuracy relativistic calculations, in connection with high-accuracy measurements, can be applied to refine these physical constants. At present, however, the accuracy of the final value for the dissociation energy of the ground level of H2 is restricted by the lack of the relativistic nuclear recoil contribution and the limited accuracy of the leading QED correction.
hartree, we calculated the dissociation energy D0,0 listed in the last column of the table. The numerical accuracy of D0,0 is estimated to be 3 × 10−8 cm−1. This estimation, however, does not account for the uncertainty originating from determination of the fundamental physical constants. All calculations reported in this work were performed with the best currently available values of the proton-to-electron mass ratio mp/me = 1836.15267389(17) and of the Rydberg constant R∞ = 109737.31568508(65) cm−1 obtained from the 2014 CODATA compilation.33 The uncertainties of both physical constants limit the accuracy of our final results. On the other hand, the problem can be reversed and future high-accuracy relativistic calculations, in connection with high-accuracy measurements, can be applied to refine these physical constants. At present, however, the accuracy of the final value for the dissociation energy of the ground level of H2 is restricted by the lack of the relativistic nuclear recoil contribution and the limited accuracy of the leading QED correction.
Table 1 Convergence of the lowest eigenvalue E0,0 (in a.u.) and of the corresponding dissociation energy D0,0 (in cm−1) for H2 with the basis set size K. A two-sector wave function was employed: (30,Ω,19.19,β(1)) and (30,Ω-2,19.19,β(2))
|
Ω
|
β
(1)
|
β
(2)
|
K
|
E
0,0
|
D
0,0
|
| 10 |
0.9304 |
2.664 |
36![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 642 642 |
−1.16402503082208 |
36118.797732723 |
| 11 |
0.953 |
3.041 |
53![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 599 599 |
−1.16402503087090 |
36118.797743437 |
| 12 |
0.978 |
3.45 |
76![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 601 601 |
−1.16402503088047 |
36118.797745538 |
| 13 |
1.011 |
3.20 |
106![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 764 764 |
−1.16402503088236 |
36118.797745953 |
| 14 |
1.039 |
2.80 |
146![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 072 072 |
−1.16402503088287 |
36118.797746064 |
| ∞ |
|
|
∞ |
−1.1640250308831(3) |
36118.79774610(3) |
3.4
J > 0 levels
We consider here rotationally excited states of the ground vibrational level (v = 0, J = 1–9). In this case the admixture of states with non-zero electronic angular momentum has to be taken into account in forming the wave function (see Section 2.2 and 3.1). However, still a vast contribution of energy comes from the Σ wave function and the main effort in the calculations has to be focused in the convergence of the energy within the space formed by the Σ basis functions. For this purpose, in analogy with the J = 0 case described above, we composed the Σ wave function of two sectors of basis functions with a common α parameter: (30,Ω,α,β(1)) and (20,Ω,α,β(2)). By increasing the shell parameter Ω we determined the extrapolated energy value and its uncertainty. Sample data illustrating the energy convergence for a selection of states are given in Table 2. A general observation made from this table is that the convergence does not deteriorate significantly with the increasing angular momentum J, so that for the highest state considered (J = 9), the uncertainty is about the same as that for J = 1, amounting to 10−13 hartree. In each case, the attained accuracy in dissociation energy is better than 5 × 10−8 cm−1.
Table 2 Convergence of the Σ-component of selected eigenvalues Ev,J (in a.u.) with the increasing size of the basis set. Two-sector wave functions have been employed: (30,Ω,α,β(1)) and (20,Ω,α,β(2)). K is the total size of the basis set and Dv,J – the dissociation energy in cm−1
|
J = 1 |
|
Ω
|
α
|
β
(1)
|
β
(2)
|
K
|
E
0,1
|
D
0,1
|
| 9 |
16.92 |
0.866 |
2.183 |
27![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 650 650 |
−1.1634851395410 |
36000.30529283 |
| 10 |
16.93 |
0.912 |
2.487 |
40![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 950 950 |
−1.1634851395785 |
36000.30530106 |
| 11 |
16.99 |
0.929 |
3.064 |
61![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 152 152 |
−1.1634851395847 |
36000.30530243 |
| 12 |
16.93 |
0.968 |
3.265 |
82![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 600 600 |
−1.1634851395863 |
36000.30530277 |
| 13 |
16.93 |
1.05 |
3.4776 |
117![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 936 936 |
−1.1634851395866 |
36000.30530283 |
| ∞ |
|
|
|
∞ |
−1.1634851395867(1) |
36000.30530285(2) |
|
J = 5 |
|
Ω
|
α
|
β
(1)
|
β
(2)
|
K
|
E
0,5
|
D
0,5
|
| 9 |
16.69 |
0.8599 |
2.282 |
28![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 756 756 |
−1.1560957546635 |
34378.52277078 |
| 10 |
15.62 |
0.8998 |
2.659 |
42![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 588 588 |
−1.1560957547011 |
34378.52277904 |
| 11 |
15.62 |
0.9225 |
3.026 |
61![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 152 152 |
−1.1560957547073 |
34378.52278040 |
| 12 |
15.62 |
0.974 |
3.300 |
85![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 904 904 |
−1.1560957547088 |
34378.52278073 |
| 13 |
15.62 |
1.013 |
3.350 |
117![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 936 936 |
−1.1560957547091 |
34378.52278079 |
| ∞ |
|
|
|
∞ |
−1.1560957547092(1) |
34378.52278082(3) |
|
J = 9 |
|
Ω
|
α
|
β
(1)
|
β
(2)
|
K
|
E
0,9
|
D
0,9
|
| 9 |
16.45 |
0.847 |
2.265 |
28![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 756 756 |
−1.1412332183826 |
31116.57309932 |
| 10 |
16.29 |
0.888 |
2.641 |
42![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 588 588 |
−1.1412332184218 |
31116.57310791 |
| 11 |
15.39 |
0.913 |
3.041 |
61![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 152 152 |
−1.1412332184285 |
31116.57310938 |
| 12 |
15.39 |
0.955 |
2.750 |
85![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 904 904 |
−1.1412332184298 |
31116.57310966 |
| 13 |
15.39 |
0.988 |
3.425 |
117![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 936 936 |
−1.1412332184301 |
31116.57310974 |
| ∞ |
|
|
|
∞ |
−1.1412332184302(1) |
31116.57310976(3) |
To evaluate the perturbational corrections E(2)Π, E(4)Π, and E(4)Δ we employed one-sector wave functions of proper symmetry. This time, the sector formally depends on a single α and three β (βΣ, βΠ, βΔ) parameters. However, numerical experiments have shown that the optimal βΔ is very close to the optimal βΣ, and for convenience it was fixed at the value of the latter, βΔ = βΣ. Table 3 contains sample results of our convergence study of the three energy corrections computed according to the formulas presented in Section 3.1. An inspection of the last three columns of the table gives a view on the rate of convergence and the estimated uncertainties of particular corrections. It also informs how fast the particular corrections grow with increasing J.
Table 3 Convergence of the Σ-, Π-, and Δ-components of selected rotational energy levels (in a.u.) with the increasing size of the basis set. One-sector wave functions have been employed: (30,Ω,α,βΣ,βΠ,βΔ). K is the total size of the basis set
|
Ω
|
α
|
β
Σ = βΔ |
β
Π
|
K
|
E
Σ
|
E
(2)Π·108 |
E
(4)Π·1013 |
E
(4)Δ·1013 |
|
J = 1 |
| 9 |
19.84 |
0.930 |
0.875 |
37![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 429 429 |
−1.163485134761 |
−3.27271900 |
−0.492866 |
0.0 |
| 10 |
19.82 |
0.973 |
0.904 |
55![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 965 965 |
−1.163485138021 |
−3.27272362 |
−0.492887 |
0.0 |
| 11 |
19.83 |
1.008 |
0.940 |
81![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 144 144 |
−1.163485138961 |
−3.27272388 |
−0.492892 |
0.0 |
| 12 |
19.84 |
1.049 |
0.968 |
114![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 716 716 |
−1.163485139347 |
−3.27272431 |
−0.492894 |
0.0 |
| ∞ |
|
|
|
∞ |
−1.1634851403(3) |
−3.272725(1) |
−0.492896(2) |
0.0 |
|
|
|
J = 5 |
| 9 |
22.19 |
0.923 |
0.873 |
58![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 669 669 |
−1.156095749888 |
−48.9145866 |
−104.5339 |
−31.0603 |
| 10 |
22.19 |
0.964 |
0.893 |
87![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 342 342 |
−1.156095753145 |
−48.9146524 |
−104.5382 |
−31.0614 |
| 11 |
22.20 |
0.999 |
0.936 |
126![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 120 120 |
−1.156095754085 |
−48.9146553 |
−104.5390 |
−31.0616 |
| 12 |
22.20 |
1.044 |
0.964 |
177![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 644 644 |
−1.156095754471 |
−48.9146609 |
−104.5395 |
−31.0618 |
| ∞ |
|
|
|
∞ |
−1.1560957548(4) |
−48.91467(1) |
−104.541(2) |
−31.0622(4) |
|
|
|
J = 9 |
| 9 |
23.90 |
0.915 |
0.860 |
58![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 669 669 |
−1.141233213617 |
−145.750039 |
−836.830 |
−259.851 |
| 10 |
23.91 |
0.958 |
0.889 |
87![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 342 342 |
−1.141233216875 |
−145.750228 |
−836.864 |
−259.857 |
| 11 |
23.91 |
0.994 |
0.926 |
126![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 120 120 |
−1.141233217812 |
−145.750240 |
−836.871 |
−259.857 |
| 12 |
23.92 |
1.034 |
0.953 |
177![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 644 644 |
−1.141233218194 |
−145.750258 |
−836.875 |
−259.858 |
| ∞ |
|
|
|
∞ |
−1.1412332186(4) |
−145.75028(2) |
−836.880(5) |
−259.859(1) |
We would like to emphasize that the perturbational approach described in Section 3.1 is numerically, within the assumed goal of accuracy, totally equivalent to the variational one. The perturbational approach requires three decompositions of pertinent chunks (![[Doublestruck H]](https://www.rsc.org/images/entities/char_e16b.gif) ΣΣ,
ΣΣ, ![[Doublestruck H]](https://www.rsc.org/images/entities/char_e16b.gif) ΠΠ, and
ΠΠ, and ![[Doublestruck H]](https://www.rsc.org/images/entities/char_e16b.gif) ΔΔ) of the Hamiltonian matrix, whereas in the variational approach the matrix must be decomposed as a whole. Because the decomposition effort is proportional to the cubic size of the matrix (∼K3), the perturbational approach is, for large matrices, significantly more effective than the variational one. We have confronted the results obtained for D0,J in both ways and obtained agreement better than 10−10 cm−1. This numerical agreement shows also that consideration of only those three corrections (E(2)Π,E(4)Π,E(4)Δ) is totally sufficient for our purposes.
ΔΔ) of the Hamiltonian matrix, whereas in the variational approach the matrix must be decomposed as a whole. Because the decomposition effort is proportional to the cubic size of the matrix (∼K3), the perturbational approach is, for large matrices, significantly more effective than the variational one. We have confronted the results obtained for D0,J in both ways and obtained agreement better than 10−10 cm−1. This numerical agreement shows also that consideration of only those three corrections (E(2)Π,E(4)Π,E(4)Δ) is totally sufficient for our purposes.
The final dissociation energies obtained for the lowest nine rotational levels J = 1,…,9 of the ground vibrational state are presented in Table 4. The total energy was composed of the EΣ energy evaluated using a two-sector wave function and the subsequent perturbational corrections E(2)Π,E(4)Π,E(4)Δ obtained from a one-sector wave function. It can be seen that the final accuracy is determined mainly by the accuracy achieved for the EΣ term. For higher J though, the uncertainty originating from E(2)Π becomes significant. The second-order correction resulting from the coupling of the nuclear rotational angular momentum with the electronic Π-state is indispensable for accurate calculations, even for the J = 1 level. This correction increases with growing J proportionally to J(J + 1) and for J = 9 contributes to the dissociation energy as much as 0.3 cm−1. The fourth-order Π-states correction and the Δ-states correction are much smaller but grow even more rapidly (∼[J(J + 1)]2) and become important when higher-J states or still higher accuracy is of interest.
Table 4 Nonadiabatic dissociation energy (D0,J) of the lowest rotational energy levels of the ground vibrational state of H2. The total as well as the Σ-, Π-, and Δ-components are given (in cm−1). For comparison, the results from the second order nonadiabatic perturbation theory (NAPT)34 are also given. The difference total-NAPT reflects the value of the higher order terms missing in the NAPT calculations
| Component |
J = 1 |
J = 2 |
J = 3 |
|
E
Σ
|
36000.30530285(2) |
35764.40769523(2) |
35413.24498004(2) |
|
E
(2)Π
|
0.00718280 |
0.02153694 |
0.04304002 |
|
E
(4)Π
|
0.00000001 |
0.00000010 |
0.00000038 |
|
E
(4)Δ
|
0.00000000 |
0.00000002 |
0.00000010 |
| Total |
36000.31248566(2) |
35764.42923228(2) |
35413.28802054(2) |
| NAPT |
36000.312413 |
35764.429157 |
35413.287941 |
|
|
| Component |
J = 4 |
J = 5 |
J = 6 |
|
E
Σ
|
34949.94357900(2) |
34378.52278082(3) |
33703.78059609(3) |
|
E
(2)Π
|
0.07165975(1) |
0.10735529(1) |
0.15007908(2) |
|
E
(4)Π
|
0.00000104 |
0.00000229 |
0.00000439 |
|
E
(4)Δ
|
0.00000030 |
0.00000068 |
0.00000133 |
| Total |
34950.01524009(2) |
34378.63013908(3) |
33703.93068089(4) |
| NAPT |
34950.015154 |
34378.630045 |
33703.930576 |
|
|
| Component |
J = 7 |
J = 8 |
J = 9 |
|
E
Σ
|
32931.16623829(3) |
32066.64655399(3) |
31116.57310976(3) |
|
E
(2)Π
|
0.19977878(3) |
0.25639928(3) |
0.31988489(4) |
|
E
(4)Π
|
0.00000759 |
0.00001216 |
0.00001837 |
|
E
(4)Δ
|
0.00000233 |
0.00000376 |
0.00000570 |
| Total |
32931.36602699(4) |
32066.90296919(4) |
31116.89301872(5) |
| NAPT |
32931.365910 |
32066.902838 |
31116.892871 |
In Table 4 we compared the total nonadiabatic dissociation energy with the energy obtained from the second order nonadiabatic perturbation theory (NAPT).34 The difference between these two numbers comes from the higher order ![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) (me/M)3 terms not included in the perturbational calculations of ref. 34.
(me/M)3 terms not included in the perturbational calculations of ref. 34.
4 Summary and outlook
The numerical results presented in this work concern only the hydrogen molecule, but the method described is applicable to any four-particle Coulomb system. The achieved accuracy surpasses that available to date for such systems. Until now, such an accuracy was available only for systems with three or fewer particles. Apart from the high accuracy, the main advantage of this method is in the formalism that enables straightforward calculations for non-zero rotational angular momentum. This feature opens up a window for accurate prediction of nonrelativistic energy for all bound levels in such systems.
The numerical results presented here constitute an introductory but indispensable part of a larger project aimed at predicting the energy levels of H2 with an accuracy of 10−6 cm−1. This part must be followed by accurate (at least 1 ppm) calculations of the leading relativistic (∼α2) and QED (∼α3) corrections as well as corrections resulting from higher-order (∼α4 and α5) contributions and other tiny effects like the finite size of the nucleus or gerade–ungerade mixing.35 We have recently evaluated the relativistic correction and the higher-order QED corrections in the Born–Oppenheimer regime.14,15 The new nonadiabatic wave functions will enable us to take into account also the finite nuclear mass effects in the corrections mentioned above.
Conflicts of interest
There are no conflicts to declare.
Acknowledgements
This research was supported by NCN Grants No. 2012/04/A/ST2/00105 (K. P.) and 2017/25/B/ST4/01024 (J. K.), as well as by a computing grant from the Poznan Supercomputing and Networking Center, and by PL-Grid Infrastructure.
References
- W. Ubachs, J. Koelemeij, K. Eikema and E. Salumbides, J. Mol. Spectrosc., 2016, 320, 1–12 CrossRef CAS.
- J. Liu, E. J. Salumbides, U. Hollenstein, J. C. J. Koelemeij, K. S. E. Eikema, W. Ubachs and F. Merkt, J. Chem. Phys., 2009, 130, 174306 CrossRef PubMed.
- J. Liu, D. Sprecher, C. Jungen, W. Ubachs and F. Merkt, J. Chem. Phys., 2010, 132, 154301 CrossRef PubMed.
- D. Sprecher, J. Liu, C. Jungen, W. Ubachs and F. Merkt, J. Chem. Phys., 2010, 133, 111102 CrossRef PubMed.
- D. Sprecher, C. Jungen, W. Ubachs and F. Merkt, Faraday Discuss., 2011, 150, 51 RSC.
- S. Kassi and A. Campargue, J. Chem. Phys., 2012, 137, 234201 CrossRef PubMed.
- D. Sprecher, M. Beyer and F. Merkt, Chimia, 2013, 67, 257–261 CrossRef CAS PubMed.
- M. Niu, E. Salumbides, G. Dickenson, K. Eikema and W. Ubachs, J. Mol. Spectrosc., 2014, 300, 44–54 CrossRef CAS.
- M. L. Niu, E. J. Salumbides and W. Ubachs, J. Chem. Phys., 2015, 143, 081102 CrossRef CAS PubMed.
- P. Wcisło, I. Gordon, H. Tran, Y. Tan, S.-M. Hu, A. Campargue, S. Kassi, D. Romanini, C. Hill, R. Kochanov and L. Rothman, J. Quant. Spectrosc. Radiat. Transfer, 2016, 177, 75–91 CrossRef.
- C.-F. Cheng, Y. R. Sun, H. Pan, J. Wang, A.-W. Liu, A. Campargue and S.-M. Hu, Phys. Rev. A: At., Mol., Opt. Phys., 2012, 85, 024501 CrossRef.
- D. Mondelain, S. Kassi, T. Sala, D. Romanini, D. Gatti and A. Campargue, J. Mol. Spectrosc., 2016, 326, 5–8 CrossRef CAS.
- J. Biesheuvel, J.-P. Karr, L. Hilico, K. S. E. Eikema, W. Ubachs and J. C. J. Koelemeij, Appl. Phys. B: Lasers Opt., 2016, 123, 23 CrossRef.
- M. Puchalski, J. Komasa and K. Pachucki, Phys. Rev. A, 2017, 95, 052506 CrossRef.
- M. Puchalski, J. Komasa, P. Czachorowski and K. Pachucki, Phys. Rev. Lett., 2016, 117, 263002 CrossRef PubMed.
- W. Kołos and L. Wolniewicz, Rev. Mod. Phys., 1963, 35, 473 CrossRef.
- W. Kołos and L. Wolniewicz, J. Chem. Phys., 1964, 41, 3674 CrossRef.
- H. M. James and A. S. Coolidge, J. Chem. Phys., 1933, 1, 825 CrossRef CAS.
- D. M. Bishop and L. M. Cheung, Phys. Rev. A: At., Mol., Opt. Phys., 1978, 18, 1846–1852 CrossRef CAS.
- C. A. Traynor, J. B. Anderson and B. M. Boghosian, J. Chem. Phys., 1991, 94, 3657–3664 CrossRef CAS.
- B. Chen and J. B. Anderson, J. Chem. Phys., 1995, 102, 2802–2805 CrossRef CAS.
- D. B. Kinghorn and L. Adamowicz, Phys. Rev. Lett., 1999, 83, 2541–2543 CrossRef CAS.
- D. B. Kinghorn and L. Adamowicz, J. Chem. Phys., 2000, 113, 4203–4205 CrossRef CAS.
- S. Bubin and L. Adamowicz, J. Chem. Phys., 2003, 118, 3079–3082 CrossRef CAS.
- S. Bubin, F. Leonarski, M. Stanke and L. Adamowicz, Chem. Phys. Lett., 2009, 477, 12–16 CrossRef CAS.
- J. Mitroy, S. Bubin, W. Horiuchi, Y. Suzuki, L. Adamowicz, W. Cencek, K. Szalewicz, J. Komasa, D. Blume and K. Varga, Rev. Mod. Phys., 2013, 85, 693–749 CrossRef.
- D. M. Fromm and R. N. Hill, Phys. Rev. A: At., Mol., Opt. Phys., 1987, 36, 1013–1044 CrossRef.
- E. Remiddi, Phys. Rev. A: At., Mol., Opt. Phys., 1991, 44, 5492–5502 CrossRef CAS.
- F. E. Harris, Phys. Rev. A: At., Mol., Opt. Phys., 1997, 55, 1820–1831 CrossRef CAS.
- K. Pachucki, Phys. Rev. A: At., Mol., Opt. Phys., 2009, 80, 032520 CrossRef.
- K. Pachucki, Phys. Rev. A: At., Mol., Opt. Phys., 2012, 86, 052514 CrossRef.
-
Y. Hida, X. S. Li and D. H. Bailey, Quad-Double Arithmetic: Algorithms, Implementation, and Application, Lbl-46996, lawrence berkeley national laboratory technical report, 2000.
- P. J. Mohr, D. B. Newell and B. N. Taylor, Rev. Mod. Phys., 2016, 88, 035009 CrossRef.
- K. Pachucki and J. Komasa, J. Chem. Phys., 2015, 143, 034111 CrossRef PubMed.
- K. Pachucki and J. Komasa, Phys. Rev. A: At., Mol., Opt. Phys., 2011, 83, 042510 CrossRef.
|
| This journal is © the Owner Societies 2018 |
Click here to see how this site uses Cookies. View our privacy policy here.  b
b
![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) n(x) with x = β|R − Re|, where β and Re are variational parameters, and
n(x) with x = β|R − Re|, where β and Re are variational parameters, and ![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) n denotes the n-th Hermite polynomial. The expansion was composed of 54 electronic terms and six hn functions yielding 147-terms in total. Because of this relatively short expansion, the obtained nonrelativistic dissociation energy D0 = 36114.7 cm−1 differed by ca. 3 cm−1 from the exact value. Nevertheless, the pioneering work by Kołos and Wolniewicz has set the foundations of the theoretical techniques for accurate calculations and, regarding the then available computing capabilities, should be considered as a great success of theory. Fifteen years later, using the same type of wave functions with significantly larger (1070-term) and carefully optimized expansion, a refined integration method, and much more powerful computers, Bishop and Cheung19 reduced the error to 0.2 cm−1. Quite a different approach, based on the quantum Monte Carlo method, was presented by Traynor et al.20 in 1991 and improved later by Chen and Anderson.21 Their trial wave function was a product of four terms ψi. The first two terms were a combination of one-electron functions centered on nuclei A and B, ψi = e−ariA + e−ariB. The third term was the Jastrow factor responsible for interparticle correlation and cusps
n denotes the n-th Hermite polynomial. The expansion was composed of 54 electronic terms and six hn functions yielding 147-terms in total. Because of this relatively short expansion, the obtained nonrelativistic dissociation energy D0 = 36114.7 cm−1 differed by ca. 3 cm−1 from the exact value. Nevertheless, the pioneering work by Kołos and Wolniewicz has set the foundations of the theoretical techniques for accurate calculations and, regarding the then available computing capabilities, should be considered as a great success of theory. Fifteen years later, using the same type of wave functions with significantly larger (1070-term) and carefully optimized expansion, a refined integration method, and much more powerful computers, Bishop and Cheung19 reduced the error to 0.2 cm−1. Quite a different approach, based on the quantum Monte Carlo method, was presented by Traynor et al.20 in 1991 and improved later by Chen and Anderson.21 Their trial wave function was a product of four terms ψi. The first two terms were a combination of one-electron functions centered on nuclei A and B, ψi = e−ariA + e−ariB. The third term was the Jastrow factor responsible for interparticle correlation and cusps 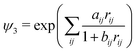 and the last term accounted for nuclear vibration and was of the Gaussian form ψ4 = e−d(R−c)2. The quantum Monte Carlo method allowed the finite basis set error to be eliminated but introduced instead a statistical (sampling) error, which in the latter calculations was of about ±0.2 cm−1. A breakthrough result has been published by Kinghorn and Adamowicz.22,23 Using a 512-term basis of explicitly correlated Gaussian functions, they have diminished the error in the nonrelativistic D0 to 1.7 × 10−3 cm−1. Later on, successively improving the optimization technique and expanding the basis set size to 10
and the last term accounted for nuclear vibration and was of the Gaussian form ψ4 = e−d(R−c)2. The quantum Monte Carlo method allowed the finite basis set error to be eliminated but introduced instead a statistical (sampling) error, which in the latter calculations was of about ±0.2 cm−1. A breakthrough result has been published by Kinghorn and Adamowicz.22,23 Using a 512-term basis of explicitly correlated Gaussian functions, they have diminished the error in the nonrelativistic D0 to 1.7 × 10−3 cm−1. Later on, successively improving the optimization technique and expanding the basis set size to 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 terms, Bubin and Adamowicz24–26 arrived at an extremely accurate solution of the four-particle Schrödinger equation to obtain D0 = 36118.79774(1)cm−1.
000 terms, Bubin and Adamowicz24–26 arrived at an extremely accurate solution of the four-particle Schrödinger equation to obtain D0 = 36118.79774(1)cm−1.
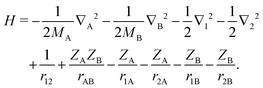
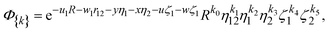
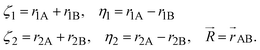
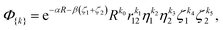
![[L with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_004c_20d1.gif) , and gives the total angular momentum
, and gives the total angular momentum ![[J with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_004a_20d1.gif) of a molecule. For this reason, the wave function ΨJ,M of a rotational level J (formally depending also on the projection of
of a molecule. For this reason, the wave function ΨJ,M of a rotational level J (formally depending also on the projection of ![[J with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_004a_20d1.gif) on the Z axis in the laboratory frame) must contain components that describe the electronic Σ, Π, and Δ,… states. In the following set of formulas we construct such a wave function and we introduce a necessary notation. The total wave function is a sum of the components with growing Λ—the eigenvalue of the
on the Z axis in the laboratory frame) must contain components that describe the electronic Σ, Π, and Δ,… states. In the following set of formulas we construct such a wave function and we introduce a necessary notation. The total wave function is a sum of the components with growing Λ—the eigenvalue of the ![[n with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006e_20d1.gif) ·
·![[L with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_004c_20d1.gif) operator
operator![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) J ≥ 0
J ≥ 0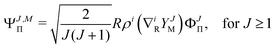
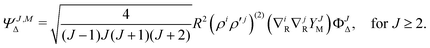
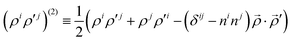
![[small rho, Greek, vector]](https://www.rsc.org/images/entities/i_char_e137.gif) ,
, ![[small rho, Greek, vector]](https://www.rsc.org/images/entities/i_char_e137.gif) ′ ≡
′ ≡ ![[small rho, Greek, vector]](https://www.rsc.org/images/entities/i_char_e137.gif) 1 or
1 or ![[small rho, Greek, vector]](https://www.rsc.org/images/entities/i_char_e137.gif) 2
2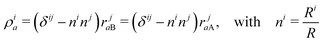
![[n with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006e_20d1.gif) ) denotes the spherical harmonic. The functions ΦJΛ represent linear expansions in the above-defined naJC basis functions (4)
) denotes the spherical harmonic. The functions ΦJΛ represent linear expansions in the above-defined naJC basis functions (4)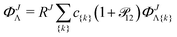
![[scr P, script letter P]](https://www.rsc.org/images/entities/char_e52f.gif) 12 means the electron permutation operator and the linear coefficients c{k} are determined variationally.
12 means the electron permutation operator and the linear coefficients c{k} are determined variationally.
![[n with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006e_20d1.gif) ), whereas the electronic angular contribution is represented in the form of the expansion (5) in Cartesian coordinates ρi. Each term of this expansion represents a function with a well-defined projection of the electronic angular momentum Λ. Moreover, the product of
), whereas the electronic angular contribution is represented in the form of the expansion (5) in Cartesian coordinates ρi. Each term of this expansion represents a function with a well-defined projection of the electronic angular momentum Λ. Moreover, the product of 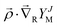 commutes with the total angular momentum operator
commutes with the total angular momentum operator ![[J with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_004a_20d1.gif) so that it preserves the correct J and M quantum numbers. Finally, this expansion is complete. In practice, though, it can be cut due to the rapidly decreasing contribution from the subsequent terms.
so that it preserves the correct J and M quantum numbers. Finally, this expansion is complete. In practice, though, it can be cut due to the rapidly decreasing contribution from the subsequent terms.![[small rho, Greek, vector]](https://www.rsc.org/images/entities/i_char_e137.gif) 1
1![[small rho, Greek, vector]](https://www.rsc.org/images/entities/i_char_e137.gif) 2(ρi1ρj2)(2) =
2(ρi1ρj2)(2) = ![[small rho, Greek, vector]](https://www.rsc.org/images/entities/i_char_e137.gif) 22(ρi1ρj1)(2) +
22(ρi1ρj1)(2) + ![[small rho, Greek, vector]](https://www.rsc.org/images/entities/i_char_e137.gif) 12(ρi2ρj2)(2).
12(ρi2ρj2)(2).![[P with combining circumflex]](https://www.rsc.org/images/entities/i_char_0050_0302.gif) . The inversion
. The inversion ![[P with combining circumflex]](https://www.rsc.org/images/entities/i_char_0050_0302.gif) reverses the sign of spatial coordinates of all particles leaving their spin unchanged, and the wave function is an eigenstate of
reverses the sign of spatial coordinates of all particles leaving their spin unchanged, and the wave function is an eigenstate of ![[P with combining circumflex]](https://www.rsc.org/images/entities/i_char_0050_0302.gif) with eigenvalues ±1. The wave function has also a definite symmetry with respect to the exchange of electrons—it is either symmetric or antisymmetric for the total electronic spin S = 0 or 1, respectively. In practice, this symmetry is enforced by acting on the spatial wave function with the
with eigenvalues ±1. The wave function has also a definite symmetry with respect to the exchange of electrons—it is either symmetric or antisymmetric for the total electronic spin S = 0 or 1, respectively. In practice, this symmetry is enforced by acting on the spatial wave function with the 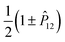 operator, where
operator, where ![[P with combining circumflex]](https://www.rsc.org/images/entities/i_char_0050_0302.gif) 12 exchanges the electron labels.
12 exchanges the electron labels.
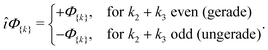
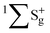 ) of H2, we observe that the subsequent rotational levels assume alternate nuclear spins. As a result, the even J levels correspond to the nuclear singlet (para-hydrogen) and the odd J levels to the triplet state (ortho-hydrogen).
) of H2, we observe that the subsequent rotational levels assume alternate nuclear spins. As a result, the even J levels correspond to the nuclear singlet (para-hydrogen) and the odd J levels to the triplet state (ortho-hydrogen).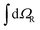 . Let us first note, that for an arbitrary scalar operator Q we have
. Let us first note, that for an arbitrary scalar operator Q we have 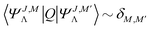 . In the simplest case of matrix elements with a scalar electronic (i.e. containing no differentiation over R) operator Qel we have
. In the simplest case of matrix elements with a scalar electronic (i.e. containing no differentiation over R) operator Qel we have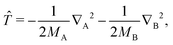
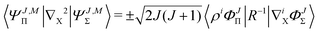
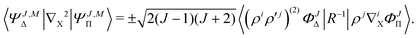
![[R with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0052_20d1.gif) =
= ![[R with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0052_20d1.gif) A −
A − ![[R with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0052_20d1.gif) B. All the remaining matrix elements vanish, so that the overlap and Hamiltonian matrices have the following block-band structure
B. All the remaining matrix elements vanish, so that the overlap and Hamiltonian matrices have the following block-band structure
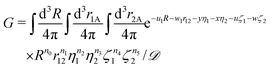
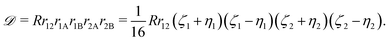
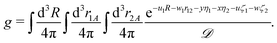
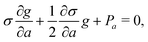
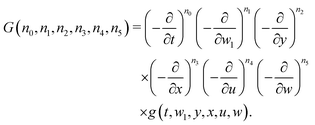
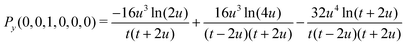
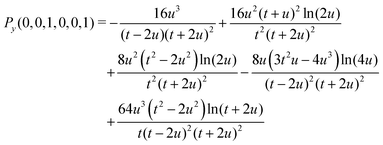
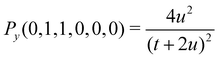
![[Doublestruck H]](https://www.rsc.org/images/entities/char_e16b.gif) and overlap
and overlap ![[Doublestruck N]](https://www.rsc.org/images/entities/char_e171.gif) matrices
matrices![[Doublestruck H]](https://www.rsc.org/images/entities/char_e16b.gif) − E
− E![[Doublestruck N]](https://www.rsc.org/images/entities/char_e171.gif) )
)![[Doublestruck C]](https://www.rsc.org/images/entities/char_e166.gif) = 0,
= 0,![[Doublestruck C]](https://www.rsc.org/images/entities/char_e166.gif) is a vector of linear coefficients from eqn (12). For all states this equation can be solved directly, e.g. by the inverse iteration method. However, due to the large size of the matrices
is a vector of linear coefficients from eqn (12). For all states this equation can be solved directly, e.g. by the inverse iteration method. However, due to the large size of the matrices ![[Doublestruck H]](https://www.rsc.org/images/entities/char_e16b.gif) and
and ![[Doublestruck N]](https://www.rsc.org/images/entities/char_e171.gif) for rotational states, it is more economical to apply the inverse iteration method only for the Σ component, and obtain the Π and Δ components from the standard perturbation theory. In other words, when J > 0, the wavefunction ΨJ,M, as defined in Section 2.2, is composed of mutually orthogonal Λ-segments. The orthogonality is manifested in the block-diagonal structure of the overlap matrix, eqn (24). The small block-off-diagonal terms of matrix
for rotational states, it is more economical to apply the inverse iteration method only for the Σ component, and obtain the Π and Δ components from the standard perturbation theory. In other words, when J > 0, the wavefunction ΨJ,M, as defined in Section 2.2, is composed of mutually orthogonal Λ-segments. The orthogonality is manifested in the block-diagonal structure of the overlap matrix, eqn (24). The small block-off-diagonal terms of matrix ![[Doublestruck H]](https://www.rsc.org/images/entities/char_e16b.gif) enable rapidly converging perturbative expansion. In this section, we supply explicit formulas for the subsequent perturbational corrections.
enable rapidly converging perturbative expansion. In this section, we supply explicit formulas for the subsequent perturbational corrections.
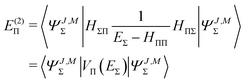
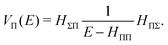
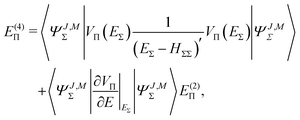
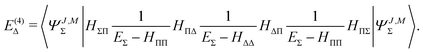
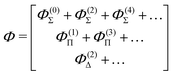
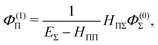
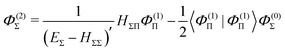
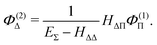
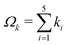 . To describe a sector of basis functions for given J and Λ values, we use a four parameter symbol (kmax0,Ω,α,β). Such a sector involves basis functions with the nonlinear parameters α and β, and with the integer powers ki fulfilling kmin0 ≤ k0 ≤ kmax0 and 0 ≤ Ωk ≤ Ω. By increasing Ω we can systematically add new basis functions to the expansion and observe the convergence of energy with an increasing total size of the basis set K.
. To describe a sector of basis functions for given J and Λ values, we use a four parameter symbol (kmax0,Ω,α,β). Such a sector involves basis functions with the nonlinear parameters α and β, and with the integer powers ki fulfilling kmin0 ≤ k0 ≤ kmax0 and 0 ≤ Ωk ≤ Ω. By increasing Ω we can systematically add new basis functions to the expansion and observe the convergence of energy with an increasing total size of the basis set K.
![[Doublestruck M]](https://www.rsc.org/images/entities/char_e170.gif)
![[Doublestruck D]](https://www.rsc.org/images/entities/char_e167.gif)
![[Doublestruck M]](https://www.rsc.org/images/entities/char_e170.gif) T decomposition of the
T decomposition of the ![[Doublestruck H]](https://www.rsc.org/images/entities/char_e16b.gif) − E
− E![[Doublestruck N]](https://www.rsc.org/images/entities/char_e171.gif) matrix followed by a solution of the linear equations set performed several times up to the assumed convergence. The matrix
matrix followed by a solution of the linear equations set performed several times up to the assumed convergence. The matrix ![[Doublestruck D]](https://www.rsc.org/images/entities/char_e167.gif) is block diagonal with blocks of the order 1 or 2, and
is block diagonal with blocks of the order 1 or 2, and ![[Doublestruck M]](https://www.rsc.org/images/entities/char_e170.gif) is unit lower triangular. The workload of the decomposition step grows with the basis size like K3 whereas that of the remainder steps like K2; therefore, for large matrices the decomposition step determines the timing of all of the computations. The linear algebra calculations, as well as the evaluation of matrix elements, were performed using extended precision arithmetics implemented with the help of the QD library.32 It enables nearly octuple precision (212 bit, 62 digits), which is sufficient to obtain the required accuracy of the energy levels considered in this work.
is unit lower triangular. The workload of the decomposition step grows with the basis size like K3 whereas that of the remainder steps like K2; therefore, for large matrices the decomposition step determines the timing of all of the computations. The linear algebra calculations, as well as the evaluation of matrix elements, were performed using extended precision arithmetics implemented with the help of the QD library.32 It enables nearly octuple precision (212 bit, 62 digits), which is sufficient to obtain the required accuracy of the energy levels considered in this work.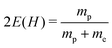 hartree, we calculated the dissociation energy D0,0 listed in the last column of the table. The numerical accuracy of D0,0 is estimated to be 3 × 10−8 cm−1. This estimation, however, does not account for the uncertainty originating from determination of the fundamental physical constants. All calculations reported in this work were performed with the best currently available values of the proton-to-electron mass ratio mp/me = 1836.15267389(17) and of the Rydberg constant R∞ = 109737.31568508(65) cm−1 obtained from the 2014 CODATA compilation.33 The uncertainties of both physical constants limit the accuracy of our final results. On the other hand, the problem can be reversed and future high-accuracy relativistic calculations, in connection with high-accuracy measurements, can be applied to refine these physical constants. At present, however, the accuracy of the final value for the dissociation energy of the ground level of H2 is restricted by the lack of the relativistic nuclear recoil contribution and the limited accuracy of the leading QED correction.
hartree, we calculated the dissociation energy D0,0 listed in the last column of the table. The numerical accuracy of D0,0 is estimated to be 3 × 10−8 cm−1. This estimation, however, does not account for the uncertainty originating from determination of the fundamental physical constants. All calculations reported in this work were performed with the best currently available values of the proton-to-electron mass ratio mp/me = 1836.15267389(17) and of the Rydberg constant R∞ = 109737.31568508(65) cm−1 obtained from the 2014 CODATA compilation.33 The uncertainties of both physical constants limit the accuracy of our final results. On the other hand, the problem can be reversed and future high-accuracy relativistic calculations, in connection with high-accuracy measurements, can be applied to refine these physical constants. At present, however, the accuracy of the final value for the dissociation energy of the ground level of H2 is restricted by the lack of the relativistic nuclear recoil contribution and the limited accuracy of the leading QED correction.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 642
642![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 599
599![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 601
601![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 764
764![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 072
072![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 650
650![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 950
950![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 152
152![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 600
600![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 936
936![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 756
756![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 588
588![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 152
152![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 904
904![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 936
936![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 756
756![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 588
588![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 152
152![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 904
904![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 936
936![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 429
429![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 965
965![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 144
144![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 716
716![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 669
669![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 342
342![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 120
120![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 644
644![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 669
669![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 342
342![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 120
120![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 644
644![[Doublestruck H]](https://www.rsc.org/images/entities/char_e16b.gif) ΣΣ,
ΣΣ, ![[Doublestruck H]](https://www.rsc.org/images/entities/char_e16b.gif) ΠΠ, and
ΠΠ, and ![[Doublestruck H]](https://www.rsc.org/images/entities/char_e16b.gif) ΔΔ) of the Hamiltonian matrix, whereas in the variational approach the matrix must be decomposed as a whole. Because the decomposition effort is proportional to the cubic size of the matrix (∼K3), the perturbational approach is, for large matrices, significantly more effective than the variational one. We have confronted the results obtained for D0,J in both ways and obtained agreement better than 10−10 cm−1. This numerical agreement shows also that consideration of only those three corrections (E(2)Π,E(4)Π,E(4)Δ) is totally sufficient for our purposes.
ΔΔ) of the Hamiltonian matrix, whereas in the variational approach the matrix must be decomposed as a whole. Because the decomposition effort is proportional to the cubic size of the matrix (∼K3), the perturbational approach is, for large matrices, significantly more effective than the variational one. We have confronted the results obtained for D0,J in both ways and obtained agreement better than 10−10 cm−1. This numerical agreement shows also that consideration of only those three corrections (E(2)Π,E(4)Π,E(4)Δ) is totally sufficient for our purposes.![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) (me/M)3 terms not included in the perturbational calculations of ref. 34.
(me/M)3 terms not included in the perturbational calculations of ref. 34.