Reconciling the valence state with magnetism in mixed-valent polyoxometalates: the case of a {VO₂F₂@V₂₂O₅₄} cluster

Abstract

The electronic structure and magnetism of the recently synthesised mixed-valent {V^VO₂F₂@V^IV/V₂₂O₅₄} (1) host–guest polyoxovanadate envisaged as a potential building block of a molecule-based quantum computer are analysed using density functional theory (DFT) and effective Hamiltonian calculations. The form of the t–J like effective Hamiltonian has been inspired by the acquired DFT data, and the valence state used in DFT calculations has been suggested by the fits to the experimental magnetic data with the effective Hamiltonian. This self-consistent approach breaks through the magnetochemical limitations of vanadium-oxo cluster 1, giving results fully concordant with the experiment and allowing us to determine the valence state of 1, which contrary to other members of this host–guest family appears to feature 9 valence electrons.

---

The use of polyoxometalates¹ (POMs) in the next-generation information technology^2–4 requires control of their electronic charge and spin states at the molecular-to-nanoscale level.⁵ One of the fields currently being pursued in POM science is the development of molecular spin qubits based on reduced metal-oxo cluster units with magnetic ground states.^6–10 Besides the exploration of the possibilities for a long quantum coherence lifetime¹¹ and scalability to a number of qubits, the development of magnetochemical methodologies to gain all-necessary insights into the potential single molecule-based quantum system before its attachment at a solid surface is mandatory.

Mixed-valent polyoxovanadates^12,13 (POVs) feature a unique interplay between molecular charge on one side and the redox (3d¹-V^IV/3d⁰-V^V) and magnetic states on the other, and as such they emerge as promising candidates for engineering molecular qubit functionality. In sufficiently symmetric mixed-valent POVs some of the valence electrons are (partially) delocalised over the cage, giving rise to magnetic effects induced by hopping of the electrons.¹⁴ In particular, a spherical POV magnetically functionalised in the void with a metal-based species through weak host–guest interactions represents an interesting prototype of a supramolecular quantum system where the distinct magnetochemical effects of the host and their operation by external stimuli will be implemented by the guest entity. The distant predecessor of such an endo-functionalised POV spin capsule is a synthetically accessible, all-inorganic {V^VO₂F₂@V^IV/V₂₂O₅₄} (1) self-assembly with isotropic quantum spin 1/2 vanadyl {V^IVO}²⁺ groups.‡ The difluorovanadate guest anion has been shown to cause drastic effects on the experimental magnetic characteristics of the vanadium-oxo host-shell.¹⁵ For such POMs it is, however, difficult to find magneto-structural relations, such as for dimers,¹⁶ and to determine precisely the valence state which is crucial for the design, modelling and optimisation of potential POM-based spin qubits. Modelling the electronic structure of POMs as 1 with delocalised electrons is challenging since the dynamics of hopping electrons must be taken into account, which leads to more complex and often computationally inaccessible effective Hamiltonians. Even if a simplified semi-classical version of a Hamiltonian is used it is often problematic to perform calculations for a full-size POM.¹⁴

Herein we have described for the first time the results of the effective Hamiltonian calculations of an aforementioned large, mixed-valent POV (1) taking into account the dynamics of the delocalised electrons. These calculations could be efficiently performed due to the use of a massively parallel computing and evolutionary algorithm. The particular form of the effective Hamiltonian was inspired by the results of DFT calculations that were introduced to shed light on the geometric and electronic peculiarities of this polyoxoanion. The self-consistent use of these two complementary theoretical techniques allows us to determine the valence state and microscopic parameters that lead to the full agreement with the experimentally measured magnetic properties of 1.

Due to similar electrochemical properties, it has been hypothesised¹⁵ that the valence state of 1 is the same as those of other {X@V₂₂O₅₄} family members (X = SCN⁻, ClO₄⁻) and features 8 valence electrons. This means that one gets a POV anion, [V^VO₂F₂@HV^IV₈V^V₁₄O₅₄]⁶⁻ (1a), with a guest monoanion, V^VO₂F₂⁻, and one proton to maintain the total charge balance. The total number of unpaired electrons cannot be determined from the susceptibility measured at high temperature since the χT curve is not saturating at room temperature. Direct redox titration was impossible due to the low solubility of the compound.¹⁵ Moreover, the simplified calculations made for 8 valence electrons did not give good fits to the magnetic field dependence of magnetisation at low temperature.¹⁵ Thus, it cannot be excluded that the valence state of 1a is different from that of SCN⁻- and ClO₄⁻-based family members and that the limited success of modelling 1a in ref. 15 is caused not only by the use of an over-simplified model but also by the wrong valence state considered. Therefore, in this paper we additionally apply our modelling to 1 in two other valence states which are the closest to 1a: [V^VO₂F₂@V^IV₇V^V₁₅O₅₄]⁶⁻ (1b) and [V^VO₂F₂@H₂V^IV₉V^V₁₃O₅₄]⁶⁻ (1c).

DFT calculations were performed for the hydrogen-free species based on 1a–1c (see technical details in the ESI†). The idealised maximal D_2d symmetry of the empty {V₂₂O₅₄} cage decreases to C_2v by inclusion of the guest VO₂F₂⁻ moiety. The optimised 1a–1c structures have slightly different geometrical parameters, but in all the cases we identified several large imaginary vibrational frequencies, revealing that the C_2v structures are not real minima. In general, V^IV/V^V mixed-valent POVs feature small gaps between the highest singly occupied and the lowest unoccupied molecular orbitals (SOMO–LUMO gaps). The C_2v structures reveal narrow gaps ranging from 0.98 eV (1a) to 0.48 eV (1c) (Fig. 1). Removing the C_2v symmetry restrictions, we re-optimised the structures with associated stabilisation energies of 0.14 eV (1a), 0.12 eV (1b) and 0.11 eV (1c). The resulting absolute (C₁) minima present significantly larger SOMO–LUMO gaps of 1.13 eV (1a) and 0.73 eV (1c). Such variations and the C_2v → C₁ energy stabilisations denote a pseudo-Jahn–Teller (PJT) effect previously described theoretically for other POMs.¹⁷ The energies and occupations of relevant MOs in Fig. 1 illustrate facts associated with the PJT effect. Furthermore, molecular reduction 1b → 1a → 1c gives a concomitant destabilisation of the occupied MOs of ∼0.15 eV per unit charge. As such, species 1a and 1c have the highest doubly occupied MOs at −7.93 and −7.75 eV and the highest SOMOs at −5.53 and −5.38 eV, respectively.

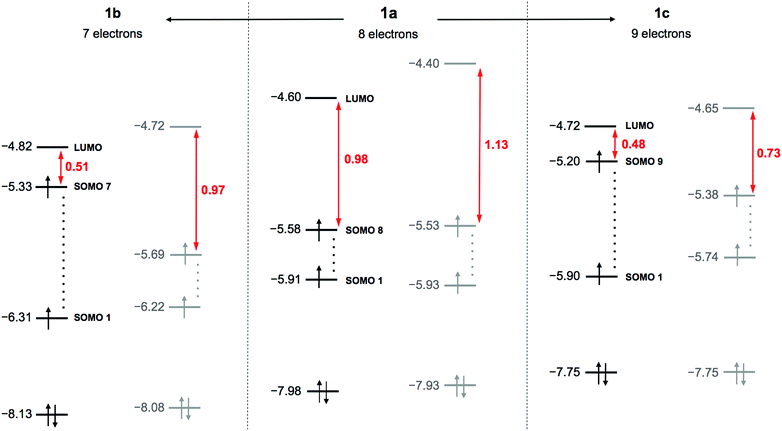Fig. 1 Electronic structure of 1, highlighting orbital energies for 1a–1c in the C_2v (black) and C₁ (grey) forms, and SOMO–LUMO energy gaps (red). Values are given in eV.

The atomic spin densities (ASDs) of 1c are nearly identical for the C_2v and C₁ minima (Table S1 and Fig. S1 in the ESI†). The apical V centres have ASDs close to 1.0 (i.e. V^IV). Neighbouring each apical site are two fully-oxidised V^V sites (ASDs 0.04–0.17). The rest of the metal centres are partially populated by unpaired electrons (ASDs 0.34–0.64) in the C_2v and C₁ minima, sharing the remaining 7 unpaired electrons of the molecule. Most unpaired electrons are delocalised over the major part of the V₂₂ framework (16 mixed-valent V atoms, see Table 1). The removal of one electron from the high symmetry structure (1c → 1a) leads to electron density loss from the central V₈ ring, but if the C₁ structure is considered, in addition to electron loss from the central ring, the two apical electrons partially delocalize over the outer V₆ rings, and the apical V^IV centres become V^IV/V. The MOs show that pure apical-like orbitals in 1c (Fig. S2, ESI,† right) delocalize over a neighbouring site in 1a, thus reducing the spin on apical sites to half (Fig. S2, ESI,† left), partially explaining that both V₆ rings gain electron density. Remarkably, the central V₈ ring has four V^V centres. Comparing this electronic distribution with that of the less stable C_2v form of 1a shows that the apical sites would be V^IV and two V^V sites would appear in each V₆ ring. No V^V atoms are found in the central ring. Another electron removal (1a to 1b) in the C_2v structure results in a net loss of one electron in both outer V₆ rings combined with an increment of one electron in the central V₈ ring, the apical centres remaining as V^IV. The electron distribution of its C₁ form is identical to that of 1a except for one electron removed from the V₆ ring situated in the proximity of the internal oxygens. Table S1 in the ESI† summarizes the relevant data discussed here.

Table 1 Numbers of V^IV, V^V and V^IV/V centres in structures 1a–1c with high (C_2v) and low (C₁) symmetry, estimated from DFT calculations

		1b (7e)	1a (8e)	1c (9e)
C 2v	V^IV	2	2	2
	V^V	8	4	4
	V^IV/V	12	16	16
C 1	V^IV	0	0	2
	V^V	8	6	4
	V^IV/V	14	16	16

---

The internal fragment orientation has some effect on the electron distribution. In the C_2v forms, 1a–1c invariably feature one electron more in the hemisphere closer to F and the C₁ form of 1b also concentrates more unpaired electrons in the F-hemisphere, likely due to the electrostatic effect of the VO₂F₂⁻ unit. However, in the more electron-rich species 1a and 1c in C₁, both hemispheres carry the same spin density. Apparently, structural distortion distributes the electron density in a more equitable way.

Species 1a–1c can be electrochemically interconverted. Taking 1a as the resting species, 1b and 1c can be obtained by oxidation or reduction with computed energies:

Oxidation: 1a → 1b + e⁻E = 5.13 eV

Reduction: 1a + e⁻ → 1cE = −4.85 eV

These theoretical values correspond to 0.37 and 0.65 eV vs. Ag/AgCl, respectively, in qualitative agreement with the measured values of 0.171 and 0.557 V.¹⁵ Considering that the reported resting potential for species 1a is close to 0.3 V vs. Ag/AgCl, reduction and oxidation can be considered to be highly accessible in terms of energy, and all three species 1a–1c could coexist in some ratio in the same medium. From the perspective of DFT calculations, species 1c can be considered to be stable: (i) This is because of its highly negative reduction energy. Taking as the reference the well-known oxidised POM structure [P₂W₁₇MoO₆₂]⁶⁻,¹⁸ the presently computed reduction of 1a to produce 1c is 0.25 eV more exothermic. This fact suggests that, in comparison, species 1c can be obtained at even lower potentials. (ii) The stability of 1c is also due to the very low energy of the highest SOMO, −5.38 eV. Although this absolute value is not self-explanatory, it can be compared to that of another member of the POV family as an indicator of the relative stability of the system. For the previously reported stable species [V₁₈O₄₂(I)]⁵⁻,^19,20 a member of the same family of compounds, we computed the HOMO as high as −4.79 eV (unpublished value). Hence, these computed electronic structures point out considerable electrochemical stability for 1c.

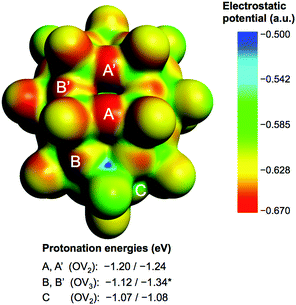
Fig. 2 shows the molecular electrostatic potential (MEP) of the hydrogen-free species 1c (see 1a and 1b in Fig S3 in the ESI†) and relevant protonation energies at bridging oxygens (red), with computed values in the −1.07 to −1.34 eV range (−24.7 to −30.9 kcal mol⁻¹). The most basic oxygen is B-type (OV₃), as expected.²¹ The energy range associated with the most nucleophilic positions, A and B (8 in total), suggests that attached protons might be itinerant within this set of oxygen atoms. See text and Fig. S4 in the ESI† for more details about the protonation of 1c.

Fig. 2 Nucleophilicity of 1c. Computed MEP and protonation energies at bridging oxygens (OV_x), labelled A–C by their location in the cage and the number, x, of linked V atoms. Energy ranges arise from the non-equivalence of oxygens of the same type due to the internal VO₂F₂ fragment. B-type positions are the most affected (*) by the relative orientation of the internal ion. The same molecular orientation is adopted in all figures.

To account for the magnetic properties of 1 and to exploit fully the results of DFT calculations concerning the distribution of valence electrons, a semi-classical t–J model has been used:¹⁴

where δ_i are occupation numbers, n stands for a number of unpaired electrons and N is a number of vanadium sites that can host a valence electron. Thus, this Hamiltonian depends not only on spin states {S_i}, but also on spin distribution {δ_i}. The values of n and N in (1) depend on the considered species and their symmetry (see Table 1 and Table S1 in the ESI†). The first term in Hamiltonian (1) describes superexchange interactions between unpaired electrons/spins (S = 1/2). The second term accounts “classically” for electron hopping, and the last term describes the Zeeman energy in magnetic field B with gyromagnetic ratio g = 1.965 and Bohr magneton μ_B. 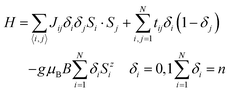The use of the fully quantum t–J model^22,23 is impossible because of the large size of Hamiltonian (1).

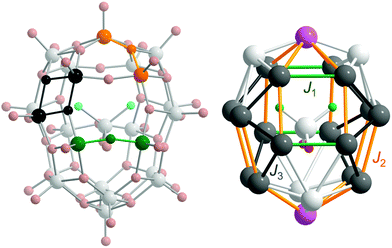
Superexchange interactions between 3d electrons at vanadium sites in 1 are mediated by three different oxo bridges: single, single-shared and double²⁴ (see Fig. 3, left). Thus, in the simplest model, at least three different exchange couplings (J_i) and also three different electron transfer couplings (t_i) must be introduced. It is possible to differentiate couplings further on the basis of distances, angles, and the neighbourhood, which gives rise to three coupling schemes (see details in the ESI†). In the idealised symmetry of 1 (C_2v), due to the inclusion of the guest anion, the number of parameters in all the coupling schemes should approximately double. For C₁ symmetry the number of parameters should be even larger. Therefore, we initially assume the symmetry of the empty cage (D_2d).

Fig. 3 Magnetic structure of 1. Left: Example of vanadium ions connected by three types of oxygen bridges: double (black), single (green), single-shared (orange). Remaining atoms: V (grey), O (light red), and F (light green). Right: Formal oxidation states of vanadium ions and exchange paths for 1a (C_2v) and 1c (C_2v and C₁) structures. Colour code (spheres): V^IV (purple), V^V (white), V^IV/V^V (grey), O (red), and F (green). Coloured sticks represent superexchange paths. Colouring of the exchange paths corresponds to coupling scheme I: J₁ (green), J₂ (orange), J₃ (black). Cage oxygens are omitted.

For 1a (C_2v) and 1c (C_2v and C₁), the distribution of formal oxidation states for V ions and exchange paths are presented in Fig. 3, right. It can be seen that this is a D_2d distribution – that of the empty cage. Unfortunately, all three coupling schemes give very poor fits (n = 8, N = 18 and δ₁₇ = δ₁₈ = 1 in eqn (1)) to the magnetic data for 1a (C_2v), as shown in Fig. S6 and Table S3 in the ESI.† Especially difficult is a proper modelling of the magnetisation. Even using the fully quantum t–J model it is impossible to model properly the magnetisation profile at low temperatures. System 1a has an even number of electrons, and hence, the ground state, which largely determines low temperature magnetism, possesses an integer total spin moment. This stands in contradiction to the experiment which suggests that magnetisation saturates at the value corresponding to the fractional total spin with S_tot = 3/2. Similarly, the same poor results can be expected for 1a in C₁ symmetry. The coupling scheme does not significantly influence the quality of the fit (see Table S3 in the ESI†). Since the same holds for 1b and 1c, in what follows we restrict our considerations only to simpler scheme I.

For 1b (C_2v), the fit (n = 7, N = 14 and δ₁₃ = δ₁₄ = 1 in eqn (1)) is still of poor quality (Fig. S7 and Table S3 in the ESI†); however, here the main problem is with a proper modelling of susceptibility at low temperatures. In C₁ symmetry the quality of the fit (n = 7, N = 14 in eqn (1)) improves, but it is impossible to model properly the minimum of the experimental susceptibility.

Finally, the best fit (n = 9, N = 18 and δ₁₇ = δ₁₈ = 1 in eqn (1)) has been obtained for 1c. Since the distribution of the formal oxidation states and the couplings follow the D_2d symmetry of the cage, it is not possible to reproduce precisely the distribution of the valence electrons in the ground state found using DFT (see Table S1, ESI†). The simplest way to break the symmetry (from D_2d to C_2v) is to assume that couplings J₁ and t₁ have different values in the F- and O-hemispheres. The best fit for such a setup (Fig. 4) has been obtained for two different parameter sets. However, only for one of them (Table 2) the probabilities to find an electron at a given V^IV/V^V site in the S_tot = 3/2 ground state resemble remarkably well the DFT atomic spin densities scaled to the number of unpaired electrons (Table 3). Yet, this distribution changes quickly at finite temperatures (see Fig. S8 in the ESI†).

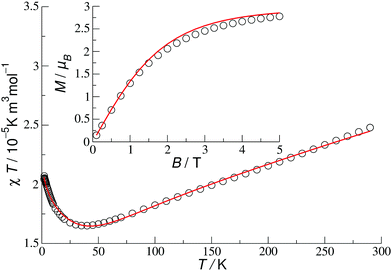Fig. 4 Molar susceptibility (B = 0.1 T) and magnetisation (T = 2 K) for 1c in coupling scheme I with asymmetric couplings J₁ and t₁ (Table 2). Circles indicate experimental data and solid lines indicate the best theoretical fit.

Table 2 Optimal Hamiltonian parameters for 1c in K

F-Hemisphere	J 1	581	t 1	1456
O-Hemisphere	J 1	385	t 1	2421
Both hemispheres	J 2	−185	t 2	3205
	J 3	609	t 3	1162

---

Table 3 Probability to find an electron (in the ground state) at V^IV/V^V sites from DFT and t–J Hamiltonian calculations for 1c in C_2v symmetry

Position in the cage	Rescaled ASD	t–J Hamiltonian
Upper ring – F-hemisphere	0.51	0.50
Inner ring	0.50–0.51	0.50
Lower ring – O-hemisphere	0.29	0.25

---

The values in Table 2 should be considered as examples since they depend on the details of the model, e.g. on the way the asymmetry of couplings is introduced, and in this sense they are not unique.§ It is important, however, that for other electronic states we were not able to obtain equally good fits.

In summary, using two complementary theoretical methods, DFT and effective Hamiltonian calculations, the magnetism and valence state of a host–guest POV {V^VO₂F₂@V^IV/V₂₂O₅₄} have been elucidated. We thus provide an example of the systematic magnetochemical treatment of a large POM with localised and delocalised electrons. Here, however, contrary to common practice,^14,25,26 the DFT technique is not used to estimate directly microscopic parameters. Our self-consistent method can indeed be applied to other nanosized, mixed-valent POMs and to mixtures of species with different valence states, which due to the easiness of the redox process cannot be excluded. The results of the application of our method to other members of the {X@V₂₂O₅₄} family and to mixtures will be published elsewhere.

Conflicts of interest

There are no conflicts of interest to declare.

Acknowledgements

K. Y. M. thanks the Deutsche Forschungsgemeinschaft (DFG) for an Emmy Noether fellowship. This work was supported by the Spanish government (Project No. CTQ2014-52774-P), the Generalitat de Catalunya (2014SGR-199 and XRQTC), and the COST Action CM1203 “Polyoxometalate Chemistry for Molecular Nanoscience” (PoCheMoN). Model Hamiltonian calculations were carried out at the Academic Computer Centre in Gdańsk and in the Poznań Supercomputing and Networking Centre, both in Poland.

Notes and references

1. U. Kortz, A. Müller, J. van Slageren, J. Schnack, N. S. Dalal and M. Dressel, Coord. Chem. Rev., 2009, 253, 2315–2327.
2. L. Vilà-Nadal, S. G. Mitchell, S. Markov, C. Busche, V. Georgiev, A. Asenov and L. Cronin, Chem. – Eur. J., 2013, 19, 16502–16511.
3. C. Busche, L. Vilà-Nadal, J. Yan, H. N. Miras, D.-L. Long, V. P. Georgiev, A. Asenov, R. H. Pedersen, N. Gadegaard, M. M. Mirza, D. J. Paul, J. M. Poblet and L. Cronin, Nature, 2014, 515, 545–549.
4. A. Balliou, G. Papadimitropoulos, G. Skoulatakis, S. Kennou, D. Davazoglou, S. Gardelis and N. Glezos, ACS Appl. Mater. Interfaces, 2016, 8, 7212–7220.
5. K. Y. Monakhov, M. Moors and P. Kögerler, Advances in Inorganic Chemistry, in Polyoxometalate Chemistry, ed. R. van Eldik and L. Cronin, Academic Press, Elsevier, Amsterdam, 2017, vol. 69, pp. 251–286.
6. J. Lehmann, A. Gaita-Ariño, E. Coronado and D. Loss, Nat. Nanotechnol., 2007, 2, 312–317.
7. J. R. Lehmann, A. Gaita-Ariño, E. Coronado and D. Loss, J. Mater. Chem., 2009, 19, 1672–1677.
8. J. M. Clemente-Juan, E. Coronado and A. Gaita-Ariño, Chem. Soc. Rev., 2012, 41, 7464.
9. S. Cardona-Serra, J. M. Clemente-Juan, E. Coronado, A. Gaita-Ariño, N. Suaud, O. Svoboda, R. Bastardis, N. Guihéry and J. J. Palacios, Chem. – Eur. J., 2015, 21, 763–769.
10. A. Palii, B. Tsukerblat, J. M. Clemente-Juan and E. Coronado, J. Phys. Chem. C, 2016, 120, 16994–17005.
11. A. Ardavan, O. Rival, J. Morton, S. Blundell, A. Tyryshkin, G. Timco and R. Winpenny, Phys. Rev. Lett., 2007, 98, 57201.
12. D. Gatteschi, L. Pardi, A. L. Barra and A. Müller, Mol. Eng., 1993, 3, 157–169.
13. K. Y. Monakhov, W. Bensch and P. Kögerler, Chem. Soc. Rev., 2015, 44, 8443–8483.
14. C. J. Calzado, J. M. Clemente-Juan, E. Coronado, A. Gaita-Ariño and N. Suaud, Inorg. Chem., 2008, 47, 5889–5901.
15. K. Y. Monakhov, O. Linnenberg, P. Kozłowski, J. van Leusen, C. Besson, T. Secker, A. Ellern, X. López, J. M. Poblet and P. Kögerler, Chem. – Eur. J., 2015, 21, 2387–2397.
16. W. Plass, Angew. Chem., Int. Ed. Engl., 1996, 35, 627–631.
17. L. Yan, X. López, J. J. Carbó, R. Sniatynsky, D. C. Duncan and J. M. Poblet, J. Am. Chem. Soc., 2008, 130, 8223–8233.
18. P. A. Aparicio, X. López and J. M. Poblet, J. Mol. Eng. Mater., 2014, 2, 1440004.
19. A. Müller, R. Sessoli, E. Krickemeyer, H. Bögge, J. Meyer, D. Gatteschi, L. Pardi, J. Westphal, K. Hovemeier, R. Rohlfing, J. Döring, F. Hellweg, C. Beugholt and M. Schmidtmann, Inorg. Chem., 1997, 36, 5239–5250.
20. O. Linnenberg, M. Moors, A. Solé-Daura, X. López, C. Bäumer, E. Kentzinger, W. Pyckhout-Hintzen and K. Y. Monakhov, J. Phys. Chem. C, 2017, 121, 10419–10429.
21. J. Y. Kempf, M. M. Rohmer, J. M. Poblet, C. Bo and M. Benard, J. Am. Chem. Soc., 1992, 114, 1136–1146.
22. J. M. Clemente-Juan, J. J. Borrás-Almenar, E. Coronado, A. V. Palii and B. S. Tsukerblat, Inorg. Chem., 2009, 48, 4557–4568.
23. J. J. Borrás-Almenar, S. Cardona-Serra, J. M. Clemente-Juan, E. Coronado, A. V. Palii and B. S. Tsukerblat, J. Comput. Chem., 2010, 31, 1321–1332.
24. O. Linnenberg, P. Kozłowski, C. Besson, J. van Leusen, U. Englert and K. Y. Monakhov, Cryst. Growth Des., 2017, 17, 2342–2350.
25. N. A. G. Bandeira, O. Sadeghi, T. J. Woods, Y.-Z. Zhang, J. Schnack, K. Dunbar, M. Nyman and C. Bo, J. Phys. Chem. A, 2017, 121, 1310–1318.
26. T. Gupta and G. Rajaraman, Chem. Commun., 2016, 52, 8972–9008.

---

Footnotes

† Electronic supplementary information (ESI) available: Details of DFT calculations and magnetochemical modelling. See DOI: 10.1039/c7cp06390c

‡ Details of the synthesis and magnetic measurements of the compound containing the title polyoxoanion can be found in our previous work (see ref. 15).

§ In all solutions which agree with DFT results there are large antiferromagnetic and smaller ferromagnetic exchange couplings in accord with a previous result.¹⁵ Moreover, such values correspond well to the experimental results: no saturation of χT at high temperature and a minimum at lower temperature (Fig. 4). Interpretation of transfer integrals is more difficult as due to their classical nature they can also comprise other effects (e.g. inter-site repulsion). However, a positive sign suggests a tendency of itinerant electrons to group together to minimize the border between occupied and unoccupied sites. For some coupling schemes also negative values appear, though they are not dominating. This is different from those in similar compounds¹⁴ where rather negative values dominate and requires further investigation.

---