The critical role of dimer formation in monosaccharides binding to human serum albumin†
Abstract
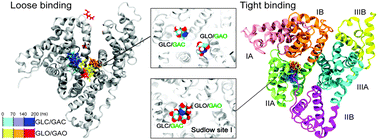
Human serum albumin (HSA) is the most abundant transport protein found in human blood. HSA is known to bind a wide range of drugs and monosaccharides, but where and how these molecules bind are largely unknown. Recently, a crystal structure of glycated HSA has been reported, and interestingly, in that structure two glucose molecules have been located in pyranose (GLC) and open chain (GLO) forms bound in the same binding pocket (Sudlow site I). Molecular simulations also proposed two binding modes of GLC and GLO (binding two ligands either in a distant location or in close contact). Yet, how HSA binds sugars in general is poorly understood. To this end, here we study the mechanism of binding glucose and its epimer galactose to HSA using alchemical free energy perturbation calculations and molecular dynamics simulations, and show why two sugar molecules appear in the bound state. We find that HSA does prefer glucose over galactose, in line with experiments, by binding glucose deeper in the pocket. Furthermore, out of the two possible binding modes suggested previously, the binding becomes tighter when the two sugars are in contact; this is achieved by a hydrogen bond connecting the two sugars and filling the large cavity of Sudlow site I as a dimer. We also find tight hydrogen bonds between open chain glucose/galactose and HSA, which includes the possible glycation site K199, while the pyranose form does not interact strongly with any characteristic residues. Thus the current result highlights the importance of dimeric structures of glucose/galactose for binding to HSA and triggering glycation/galactation.
- This article is part of the themed collection: Complex molecular systems: supramolecules, biomolecules and interfaces


 Please wait while we load your content...
Please wait while we load your content...