Well-ordered self-assembled nanostructures of block copolymer films via synergistic integration of chemoepitaxy and zone annealing†
Liangshun
Zhang
 *,
Lingling
Liu
and
Jiaping
Lin
*,
Lingling
Liu
and
Jiaping
Lin
 *
*
Shanghai Key Laboratory of Advanced Polymeric Materials, State Key Laboratory of Bioreactor Engineering, Key Laboratory for Ultrafine Materials of Ministry of Education, School of Materials Science and Engineering, East China University of Science and Technology, Shanghai 200237, China. E-mail: zhangls@ecust.edu.cn; jlin@ecust.edu.cn
First published on 28th November 2017
Abstract
It is an extremely challenging task to fabricate macroscopically well-ordered nanostructures of block copolymers in a limited annealing time. In this work, we propose a novel integrated strategy of chemoepitaxy and zone annealing to direct the self-assembly of lamella-forming block copolymers. Large-scale numerical simulations corroborate that the integrated strategy has the capability to generate well-aligned and well-oriented lamellae over a macroscopic area via the synergy between the alignment guidance of the chemical template and the defect annihilation of zone annealing, even though the guiding stripes of the chemical template are extremely sparse. It is further demonstrated that the effective annealing time to achieve the well-ordered nanostructures is strongly dependent upon the pitch of guiding stripes and the thickness of block copolymer films. This work provides an instructive example for boosting the directing efficiency of chemoepitaxy through the integrated strategy, and lays the groundwork for rapidly fabricating well-ordered nanostructures of block copolymer nanolithography.
Introduction
Self-assembly of block copolymer films into a diversity of periodically ordered structures with a length scale of 10–30 nm, beyond the resolution limits of conventional photolithography tools, renders them a cost-efficient alternative to electron beam lithography.1–8 However, conventional (‘untemplated’) self-assembly of block copolymer films is insufficient for the precise large-area nanofabrication in the semiconductor industry due to the inherent propensity of defective nanostructures. One of the most appealing proposals to yield the defect-free nanostructures is the directed self-assembly (DSA) of block copolymer films, which integrates the advantages of the conventional lithographic technique and the self-assembly natures of polymer molecules.9–22 Two types of directing methods are well developed on the basis of chemical (termed as chemoepitaxy) and topographical (graphoepitaxy) templates. In the chemoepitaxy, the patterns of block copolymer films are programmed by chemically guiding stripes, whose pitch is generally commensurate with the natural period of the self-assembled nanostructures.9,10One of the most concerned issues in DSA is the directing efficiency, which determines the manufacturing cost of the patterning technique. In the chemoepitaxy or other related methods, it is revealed that there exists a bottleneck in the directing efficiency, which is quantified by density multiplication abbreviated as DM (defined as the ratio of the density of self-assembled domains to that of guiding stripes).18,19,23,24 Specifically, an upper limit of the directing efficiency in the chemoepitaxy is restricted to a small integer multiple (i.e., DM ≤ 4), which is recorded in the experiments.19 On the basis of dynamic self-consistent field theory, this limit is also confirmed by the numerical simulations for the system of template-guided block copolymers.25 More importantly, the numerical simulations reveal the underlying mechanisms for the presence of an efficiency limit, which originates from the existence of kinetically arrested defects in the self-assembled nanostructures guided by the short-range fields.
In contrast to these short-range fields, several other methods including shear flows, thermal gradients and electric fields, are also proposed to achieve the perfectly ordered nanostructures through removal of long-lived defects or grain boundaries.26–39 Particularly, utilization of spatially and temporally variable fields (now designated as zone annealing) is a promising scheme for annihilating the kinetically arrested defects in a short time.29,32 In the course of zone annealing of block copolymers, the evolution of self-assembled nanostructures is restricted to a narrow region, resulting in faster ordering kinetics. Unfortunately, one major drawback of this method is that the zone annealing typically produces the self-assembled nanostructures with poorly registered orientation at a given location. As a consequence, it is difficult to fabricate organic materials of block copolymers satisfying specific application-determined requirements.
Although previous works successfully demonstrated an improvement of long-range order of nanostructures via the method of either chemoepitaxy or zone annealing, it is highly desirable to develop a protocol that integrates the advantages of both of these methods into one process.40,41 More recently, integration of the chemical template with the zone annealing was theoretically proposed in our group to program the alignment of self-assembled nanostructures.25 In that work, it was shown that the well-ordered nanostructures with a controllable alignment are produced in a short annealing time, even though the arrangement of guiding stripes is extremely sparse. In experiments, the combinations of various DSA processes are attracting interest due to the possible achievement of exceptionally defect-free, registered nanostructures in wide motifs.42–50 As a consequence, the strategy of synergistically integrating the directing methods reveals a novel route of directed self-assembly for fabricating the perfectly ordered nanostructures in a limited time.
It is worthwhile emphasizing that the numerical simulations of dynamic self-consistent field theory (DSCFT) for the DSA of block copolymers were performed in the two-dimensional space,25 which cannot properly capture the morphological evolution of nanostructures programmed by the chemically guiding stripes. In order to provide useful insights into the DSA of block copolymers, it is convenient to carry out the numerical simulations in the three-dimensional (3D) space. However, the recursive calculations of inverse problem of density fields in the DSCFT lead to hugely intensive computation in 3D space.51 To our knowledge, very few DSCFT simulations in the 3D space for the DSA of block copolymers have been reported. We herein utilize the acceleration technique via graphics-processing-units to address this challenge, which offers a large acceleration ratio for solving the field-theoretic equations of polymer fluids. Such a technique is an extension of our parallel algorithm of static self-consistent field theory.52
Beyond developing the parallel algorithm for solving the equations of DSCFT in the 3D space, we report the directed self-assembly of template-guided block copolymers in the presence of zone annealing. The more sophisticated method is able to reproduce the findings of two-dimensional simulations. More importantly, the 3D numerical simulations of DSCFT capture the effect of the film thickness on the programmed nanostructures and their formation process, which cannot be properly predicted by the two-dimensional simulations. We expect that the present work offers a rational understanding of the ordering behavior of nanostructures registered by the integrated method as well as some helpful information for designing the kinetic process of directed self-assembly.
Computational model
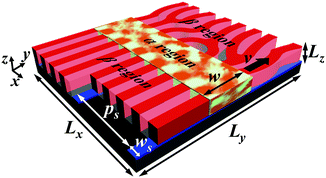
Full technical details of the dynamics self-consistent field theory for the directed self-assembly of block copolymers in the presence of dual fields can be found in Part A of the ESI.† In brief, the AB block copolymer films with dimension Lx × Ly × Lz are confined between two hard walls, which are schematically illustrated in Fig. 1. The substrate or the bottom wall (represented by black color) contains the chemically guiding stripes with pitch ps and width ws. The top wall is neutral and represented by a transparent color. The free energy functional is deduced from the standard Hamiltonian in the framework of the field-theoretic model.53 The evolution kinetics of block copolymers obeys the Cahn–Hilliard–Cook equations with local coupling approximation.51,54 For the model of zone annealing (Fig. 1),55–58 the Flory–Huggins interaction parameters of block copolymers in the α and β regions have the minimum value (χN)min and the maximum value (χN)max, respectively. The parameter w is used to indicate the zone width or the width of the α region, which is moved by velocity v.In the parameter settings, the maximum Flory–Huggins interaction parameter (χN)max of symmetric block copolymers has a value of 20.0. Under these conditions, the natural period of lamellae in the bulk is identified as L0 ∼ 4.0Rg, where Rg is the ideal gyration radius of polymer chains. The discrete time for the Cahn–Hilliard–Cook equations is Δt = 0.2τ, where τ is the time unit. We assume that the mobility coefficients in the different zones are invariable. The minimum Flory–Huggins interaction parameter (χN)min is chosen as 12.0, where the defects have the capability to be annihilated in a limited time. To efficiently achieve the well-ordered vertical lamellae, the width of guiding stripes is set as the optimal value ws ∼ 0.5L0 (i.e., ws = 1.8Rg).59,60 For the sake of simplicity, the pitch of stripes at each template is assumed to be an integer multiple of the natural period of lamellae.
We perform the numerical simulations in the three-dimensional boxes under the periodic boundary conditions in the x and y directions and the no-flux boundary condition in the z direction. In order to ensure that the simulation boxes are large enough, the dimensions of boxes in the x and y directions are set as ∼72.0Rg × 72.0Rg, which are discretized by the 288 × 288 lattices. The film thickness Lz is set in the range from 2.0Rg to 6.0Rg. Under these settings of box dimensions, the block copolymers self-assemble into 18 domains of lamellae. As far as we know, this is the first example of DSCFT simulations in super-large boxes for the directed self-assembly of block copolymers. To overcome the computational task, the GPGPU (General-Purpose Graphics Processing Unit) using the NVIDIA® CUDA™ architecture is adopted to accelerate the numerical solutions of DSCFT equations of polymeric fluids. The timing of GPGPU parallel computing is significantly shorter than that of calculations running on a single CPU core, which is demonstrated in Fig. S1 of the ESI.† For more details about the model please refer further to our previous works.58,61,62
Results and discussion
In a recent work, we have examined the ordering behavior of self-assembled nanostructures simultaneously subjected to the static field of the chemical template and the dynamic field of zone annealing in the two-dimensional space.25 It was demonstrated that the long-lived defects of lamellae registered by the sparse stripes are efficiently annihilated through incorporating a spatially and temporally dependent field. It should be pointed out that the two-dimensional simulations cannot appropriately evaluate the effect of the film thickness on the efficiency of the dual-field method in the ordering process of self-assembled nanostructures. In the present model, one remarkable improvement is incorporation of the film thickness (Fig. 1), which has an important effect on the ordering degree of programmed nanostructures in realistic experiments.63–65 In order to take the film thickness into account, we perform the large-scale simulations of DSCFT in the 3D space to probe into the ordering behavior of self-assembled nanostructures of symmetric block copolymers directed by the dual fields.The initial configurations of dual-field simulations are metastable states, which are obtained from the calculations of the chemical template alone. To obtain the metastable configurations of template-guided block copolymers, the calculations start from a disordered state but the zone annealing is switched off. Fig. S2 of the ESI† depicts the morphological evolution of symmetric block copolymers at various values of the stripe pitch and film thicknesses. In general, the disordered state quickly evolves into microphase-separated nanostructures. However, for a quenching system with a larger value of the stripe pitch or film thickness, the configurations of nanostructures still contain lots of imperfections even after a long-time running due to a kinetically slow process of defect annihilation. It is worth mentioning that the long-lived defects are maintained in the pattern in spite of further extension of the simulation time. These observations provide clear evidence that the chemical template with sparsely guiding stripes is insufficient to fabricate the defect-free nanostructures of block copolymers over a macroscopic area in a short time. Such defective nanostructures of template-guided block copolymers are selected as the initial states of dual-field simulations. Below, we will exemplify how integrating the chemical template with the zone annealing is able to achieve the defect-free nanostructures throughout the films in a limited time.
Given thickness of films
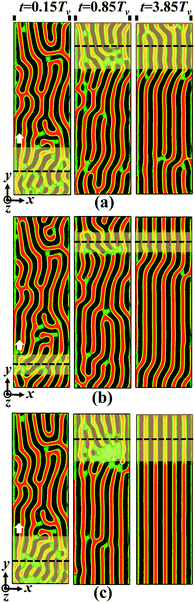
We first focus on the directing efficiency of the dual-field method for the ordering behavior of self-assembled nanostructures at a given film thickness. Fig. 2 shows the morphological evolution of template-guided block copolymers in conjunction with the zone annealing under the conditions of various zone widths and moving velocities. Fig. S3 of the ESI† also illustrates the three-dimensional view of programmed nanostructures. The stripe pitch and the film thickness are respectively set as ps = 6L0 and Lz = 0.75L0, where the natural period of lamellae has a value of L0 = 4.0Rg for the case of (χN)max = 20.0. The moving pathway of the α region is always parallel to the direction of guiding stripes. We utilize the characteristic time Tv (represents the period of zone annealing from the bottom to top of the sample at the moving velocity v) to normalize the simulation times, which are annotated at the top of images. In the initial configuration, the lamellar nanostructures guided by the sparse stripes have lots of long-lived defects (Fig. S2a of ESI†). As the spatially localized, mobile region is introduced into the pattern of defective lamellae, the defects in the α region become unstable and their annihilation is markedly accelerated.66 Subsequently, the long-lived defects in the α region are partially annihilated. The events of imperfection elimination sequentially arise through periodically moving the α region from bottom to top. Finally, the defective lamellae evolve into the highly ordered nanostructures. As a consequence, the ordering degree of lamellar patterns has a remarkable improvement due to the incorporation of zone annealing, in comparison with the initial configuration.Inspecting Fig. 2 for more details, one can also examine the directing efficiency of the integrated strategy by qualitatively comparing the morphological evolution of self-assembled nanostructures under the conditions of various zone widths and moving velocities. When the α region is moved quickly, lots of defects are annihilated but some of the grain boundaries are maintained in the lamellar pattern (Fig. 2a). Similarly, in the case of the narrower α region, the block copolymers remain the configuration of defective lamellae (Fig. 2b). As the zone width and the moving velocity are respectively set as w = 5L0 and v = 0.06![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) , the kinetically arrested defects are completely annihilated, and the block copolymers reach the configuration of defect-free standing lamellae, which are illustrated in Fig. 2c. These findings manifest the fact that the zone annealing has the capability to efficiently annihilate the long-lived defects and rapidly access the well-ordered nanostructures over a macroscopic area, in spite of the case of the chemical template with a sparse arrangement of guiding stripes.
, the kinetically arrested defects are completely annihilated, and the block copolymers reach the configuration of defect-free standing lamellae, which are illustrated in Fig. 2c. These findings manifest the fact that the zone annealing has the capability to efficiently annihilate the long-lived defects and rapidly access the well-ordered nanostructures over a macroscopic area, in spite of the case of the chemical template with a sparse arrangement of guiding stripes.
In order to quantify the ordering degree of lamellar nanostructures within the pattern, we calculate the order parameter Sα along the α direction given by67
| Sα(t) = 〈〈ϕ(r,t)〉α2/〈ϕ(r,t)2〉α〉β,γ |
Fig. 3 displays the temporal evolution of order parameters Sy and Sz of self-assembled nanostructures under the conditions of various zone widths and moving velocities. Each point represents an average over three independent runs. Note that the abscissa is normalized by the period Tv of zone annealing. A common feature of all the plots is that the ordering degree of lamellar nanostructures is increased through incorporation of zone annealing into the system of template-guided block copolymers due to the elimination of imperfections. Another common feature of all the examples is the fast growth of order parameters during the first passage of zone annealing. In each curve, the order parameters Sy and Sz reach their steady values at the fourth passage of zone annealing.
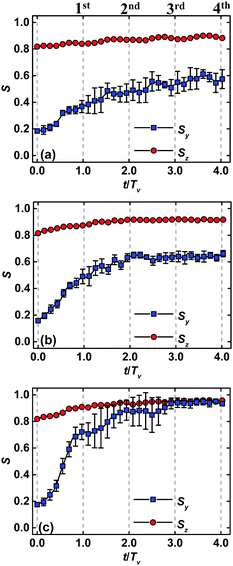 | ||
Fig. 3 Temporal evolution of order parameters Sy and Sz of lamellar nanostructures of template-guided block copolymers in conjunction with zone annealing. The zone width and the moving velocity are respectively (a) w = 5.0L0 and v = 0.12![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) , (b) w = 0.25L0 and v = 0.06 , (b) w = 0.25L0 and v = 0.06![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) and (c) w = 5.0L0 and v = 0.06 and (c) w = 5.0L0 and v = 0.06![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) . Other parameter settings of simulations are the same as those in Fig. 2. All the dual-field simulations start from the same initial configuration, but various random seeds. Each point represents an average over three independent runs. For the sake of clarity, the error bars standing for the standard deviations are only drawn for the case of Sy. . Other parameter settings of simulations are the same as those in Fig. 2. All the dual-field simulations start from the same initial configuration, but various random seeds. Each point represents an average over three independent runs. For the sake of clarity, the error bars standing for the standard deviations are only drawn for the case of Sy. | ||
In spite of the similarity mentioned above, there are also some remarkable differences among these plots in Fig. 3. In particular, the order parameter Sz remains a larger value, while the value of order parameter Sy is increased in the course of directed self-assembly of the dual fields. Under the circumstance of film thickness Lz = 0.75L0, the A-attractive stripes guide the polymer molecules to self-assemble into the standing lamellae, but lots of imperfections are also generated between the sparsely guiding stripes. These phenomena lead to a larger value of Sz but a smaller value of Sy for the initial configuration of dual-field simulations. As the zone annealing is incorporated into the system, the orientation of lamellar nanostructures is still maintained in the α region, suggesting that the annealed pattern remains a larger value of Sz along the z direction. The defect annihilation in the annealed zone has a chance to be realized and a higher ordering degree along the y direction can be achieved in the pattern. Another salient feature of the integrating method is that the ordering degree of final nanostructures is strongly dependent upon the zone width and the moving velocity. For instance, both the steady values of order parameters Sy and Sz approach one for the case of w = 5.0L0 and v = 0.06![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) , indicating the achievement of well-ordered nanostructures (Fig. 3c). Increasing the moving velocity or decreasing the zone width results in the lower value of Sy, implying that the long-lived defects are maintained in the pattern (Fig. 3a and 3b).
, indicating the achievement of well-ordered nanostructures (Fig. 3c). Increasing the moving velocity or decreasing the zone width results in the lower value of Sy, implying that the long-lived defects are maintained in the pattern (Fig. 3a and 3b).
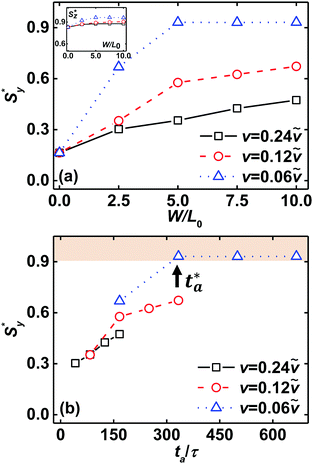
To explicitly estimate the directing efficiency of zone annealing for the nanostructures of template-guided block copolymers, we introduce steady values Sy* and Sz* of order parameters. These quantities are defined as the plateau values of order parameters at the later stage of zone annealing simulations. Fig. 4a plots the steady values Sy* and Sz* of order parameters in terms of the zone width w under various moving velocities. w = 0 corresponds to the case of the initial configuration of dual-field simulations. As the zone width becomes broad under the fixed moving velocity, the resident time of polymer molecules in the α region becomes longer to re-assemble themselves; thus, the kinetically arrested defects have an opportunity to be annihilated and a higher ordering degree of nanostructures is achieved. From Fig. 4a, it is also found that lowering the moving velocity leads to a higher ordering degree of lamellar nanostructures. These observations are similar to the case of Sz* (the inset of Fig. 4a). In other words, the introduction of zone annealing further encourages the lamellae to orient along the z direction, leading to an increase of Sz*. In particular, under the conditions of w ≥ 5.0L0 and v = 0.06![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) , the defect annihilation is completely realized in the spatially localized, mobile α region, and the steady order parameters Sy* and Sz* are both larger than 0.9, suggesting that the template-guided block copolymers in conjunction with the zone annealing self-assemble into the well-aligned and well-oriented structures under the condition of a short annealing time.
, the defect annihilation is completely realized in the spatially localized, mobile α region, and the steady order parameters Sy* and Sz* are both larger than 0.9, suggesting that the template-guided block copolymers in conjunction with the zone annealing self-assemble into the well-aligned and well-oriented structures under the condition of a short annealing time.
Unlike the oven annealing, the block copolymers reside in the α region over the effective annealing time ta, which provides a fundamental understanding about the effects of zone width and moving velocity on the change of order parameters. The quantity defined as ta ≡ w/v is tuned by the zone width and the moving velocity. As a typical example, Fig. 4b presents the steady order parameter Sy* as a function of the effective annealing time ta. When the moving velocity is high or the zone width is narrow, the effective annealing time is too short to eliminate a large number of imperfections, leading to the maintenance of defective lamellae. Increasing the effective annealing time (corresponds to a decrease of moving velocity or an increase of the zone width) eliminates the imperfections, resulting in the formation of well-ordered nanostructures over a large area. Especially, as the effective annealing time exceeds ∼333τ (i.e., w = 5.0L0 and v = 0.06![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) ), the template-guided block copolymers in conjunction with the zone annealing are directed into the defect-free structures. We herein define such a value as critical annealing time ta*.
), the template-guided block copolymers in conjunction with the zone annealing are directed into the defect-free structures. We herein define such a value as critical annealing time ta*.
It is worth mentioning that the zone annealing with various combinations of moving velocity v and zone width w has the same effective annealing time, but may produce different ordering degrees of nanostructures. For instance, the zone annealing with w = 10.0L0 and v = 0.12![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) or w = 5.0L0 and v = 0.06
or w = 5.0L0 and v = 0.06![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) has the effective annealing time ta ≈ 333τ. The former produces the defective lamellae, whereas the latter yields the defect-free lamellae. Even though the different ordering degrees of nanostructures are obtained, we choose ta* = 333τ as the critical annealing time under the condition of the pitch ps = 6L0 of guiding stripes.
has the effective annealing time ta ≈ 333τ. The former produces the defective lamellae, whereas the latter yields the defect-free lamellae. Even though the different ordering degrees of nanostructures are obtained, we choose ta* = 333τ as the critical annealing time under the condition of the pitch ps = 6L0 of guiding stripes.
Fig. 5 illustrates the relationship between the critical annealing time and the pitch of chemically guiding stripes at the film thickness Lz = 0.75L0. The critical annealing time is strongly dependent upon the pitch of guiding stripes. Specifically, when the guiding stripes are dense, the defective lamellae of block copolymers rapidly evolve into the defect-free nanostructures. In the meantime, the lamellae are aligned along the direction of guiding stripes, and are oriented along the normal of substrates. As the guiding stripes become sparse, the block copolymers require a longer annealing time to reorganize into the defect-free, standing lamellae. Thus, one can reach a conclusion that the formation of long-range ordered nanostructures with controlled orientation is strongly dependent upon the stripe pitch and the effective annealing time, which are the main factors to design the dual-field strategy of directed self-assembly for creating the macroscopically ordered materials. These examples also illustrate an instructive strategy that integration of the dual fields (e.g., the chemically guiding stripes dictate the overall orientation and alignment of lamellae and the zone annealing locally removes the imperfections) can significantly extend the process window of chemoepitaxy towards the defect-free patterns and accelerate the ordering kinetics of metastable configurations.
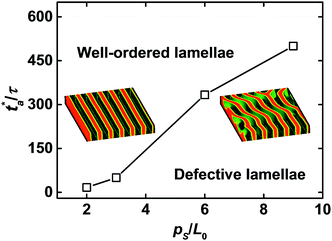 | ||
| Fig. 5 Critical value of the effective annealing time in terms of the pitch ps of guiding stripes. The definition of the critical value is depicted in Fig. 4b. The line indicates the approximate boundary between the well-ordered and defective lamellae. The film thickness is set as Lz = 0.75L0. Insets illustrate the typical configurations of well-ordered and defective lamellae. | ||
In our previous work, the numerical simulations of theoretical model were implemented in the two-dimensional space to explore the directed self-assembly of block copolymers in the presence of dual fields.25 It was highlighted that the dual-field method facilitates the annihilations of kinetically arrested defects and the formation of well-ordered nanostructures. For instance, the template-guided block copolymers in conjunction with the zone annealing with w = 8.0L0 and v = 0.75![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) (corresponds to the effective annealing time ta ≈ 43τ) are directed to form the well-aligned nanostructures, which is demonstrated in Fig. 7 of ref. 25. However, in the three-dimensional simulations of the dual-field method, the block copolymers at the film thickness Lz = 0.75L0 are guided to self-assemble into the defective lamellae under these parameter settings (Fig. 5, case of ps = 6L0). Fortunately, a decrease of moving velocity results in the achievement of long-range ordered structures. Comparison of the observations between the two- and three-dimensional simulations of DSCFT verifies the fact that the film thickness is a significant factor to affect the self-assembled nanostructures of block copolymers directed by the dual fields.
(corresponds to the effective annealing time ta ≈ 43τ) are directed to form the well-aligned nanostructures, which is demonstrated in Fig. 7 of ref. 25. However, in the three-dimensional simulations of the dual-field method, the block copolymers at the film thickness Lz = 0.75L0 are guided to self-assemble into the defective lamellae under these parameter settings (Fig. 5, case of ps = 6L0). Fortunately, a decrease of moving velocity results in the achievement of long-range ordered structures. Comparison of the observations between the two- and three-dimensional simulations of DSCFT verifies the fact that the film thickness is a significant factor to affect the self-assembled nanostructures of block copolymers directed by the dual fields.
Effect of the film thickness
Next, we investigate the effect of film thickness on the directed self-assembly of block copolymers in the presence of the dual fields of the chemical template and zone annealing. Fig. 6 shows the morphological evolution of assembled structures of symmetric block copolymers at the film thickness Lz = 1.00L0. The pitch of chemically guiding stripes has a value of ps = 3L0. The zone width and the moving velocity are chosen as w = 5.0L0 and v = 0.15![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) , respectively. In the initial configuration, the lamellar pattern is filled with lots of defects forming multiple bridges to the neighboring A-rich domains (Fig. S2b of the ESI†). The incorporation of zone annealing leads to the rearrangement of block copolymers and the annihilation of long-lived defects. As shown in Fig. 6a and b, the grains of lamellar nanostructures become large and a higher ordering degree is achieved. Through continuously moving the annealed zone, the block copolymers on the prepatterned substrate are directed to re-assemble into the well-oriented and well-aligned nanostructures, which are illustrated in Fig. 6c. The observations from Fig. 6 provide substantial evidence that the locally orientated and poorly aligned lamellae are re-organized into the well-ordered nanostructures via the introduction of an annealed zone with a lower Flory–Huggins interaction parameter. It should be mentioned that the block copolymers at the film thickness Lz = 1.25L0 cannot self-assemble into the defect-free nanostructures under the circumstances of w = 5.0L0 and v = 0.15
, respectively. In the initial configuration, the lamellar pattern is filled with lots of defects forming multiple bridges to the neighboring A-rich domains (Fig. S2b of the ESI†). The incorporation of zone annealing leads to the rearrangement of block copolymers and the annihilation of long-lived defects. As shown in Fig. 6a and b, the grains of lamellar nanostructures become large and a higher ordering degree is achieved. Through continuously moving the annealed zone, the block copolymers on the prepatterned substrate are directed to re-assemble into the well-oriented and well-aligned nanostructures, which are illustrated in Fig. 6c. The observations from Fig. 6 provide substantial evidence that the locally orientated and poorly aligned lamellae are re-organized into the well-ordered nanostructures via the introduction of an annealed zone with a lower Flory–Huggins interaction parameter. It should be mentioned that the block copolymers at the film thickness Lz = 1.25L0 cannot self-assemble into the defect-free nanostructures under the circumstances of w = 5.0L0 and v = 0.15![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) (Fig. S4 of ESI†), where the grain boundary is maintained in the system.
(Fig. S4 of ESI†), where the grain boundary is maintained in the system.
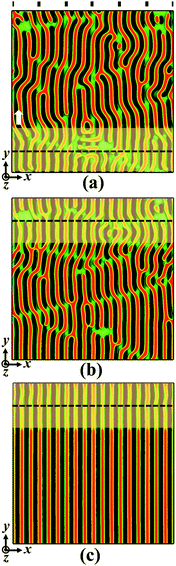 | ||
Fig. 6 Morphological evolution of self-assembled nanostructures programmed by the dual fields of the chemical template and zone annealing at film thickness Lz = 1.00L0. The zone width and the moving velocity are respectively set as w = 5.0L0 and v = 0.15![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) , where the period Tv of zone annealing has a value of 480τ. The simulation time is (a) t = 0.15Tv, (b) t = 0.85Tv and (c) t = 4.0Tv. The pitch of chemically guiding stripes is ps = 3L0. The representations of colors are the same as those in Fig. 2. , where the period Tv of zone annealing has a value of 480τ. The simulation time is (a) t = 0.15Tv, (b) t = 0.85Tv and (c) t = 4.0Tv. The pitch of chemically guiding stripes is ps = 3L0. The representations of colors are the same as those in Fig. 2. | ||
In comparison with the case of film thickness Lz = 0.75L0 as shown in Fig. 2, a salient feature of structural evolution of block copolymer films emerges (Fig. 6). To clearly monitor the process of defect annihilation, the bottom view of morphological evolution is depicted in Fig. S5 of the ESI.† As the film thickness is increased, the block copolymers guided by the chemical template alone do not form the vertically orientated lamellae throughout the film (Fig. S5a of the ESI†). In the intermediate stage of zone annealing, the block copolymers near the substrate achieve the highly aligned lamellae (Fig. S5b of the ESI†), whereas the nanostructures near the top wall retain the state of misaligned grains (Fig. 6b). Subsequently, the horizontal boundary separated the top and bottom grains gradually moves upwards, i.e., the highly aligned bottom grain grows in thickness whereas the misaligned top grains become thinner. Eventually, the block copolymers are guided to re-assemble into the vertically orientated lamellae throughout the film (Fig. 6c and Fig. S5c of the ESI†). Therefore, the integrated method of the chemical template and zone annealing not only helps the lamellae to align along the stripe direction, but also induces the regulation of lamellar orientation.
As stated above, the defect annihilation of nanostructures subjected to the dual fields is driven from the prepatterned substrate upward to the top neutral wall. Such a mechanism of defect annihilation is also identified in the system of block copolymers directed by the chemical template with a dense arrangement of chemical stripes.68,69 In the thin film, the block copolymers first wet the stripes with the correct blocks near the substrate, but form the fingerprint pattern farther away from the substrate. As the assembly time slips by, the defective structures eventually evolve into the well-ordered, standing lamellae via the movement of grain boundaries.
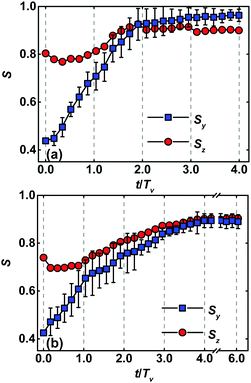
Fig. 7 depicts the temporal evolution of order parameters Sy and Sz of lamellar nanostructures registered by the integrated method at the film thickness Lz = 1.00L0 and 1.25L0. In the initial configuration of dual-field simulations, the order parameters of lamellar nanostructures have smaller values. In the first and second passages of zone annealing, the systems of template-guided block copolymers manage to get away the arrested configuration because of the acceleration of orientation rearrangement and defect removal. These facts result in a rapid increase of order parameters Sy and Sz. In the subsequent passages of zone annealing, the highly ordered lamellae are realized through further eliminating the imperfections. However, the temporal evolution of order parameters in these stages becomes slow, because of the existence of grain boundaries in the pattern. In particular, the grain boundaries of lamellar nanostructures at the film thickness Lz = 1.00L0 are successfully removed by the zone annealing with width w = 5.0L0 and moving velocity v = 0.15![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) . The grain boundary of lamellar nanostructures at the film thickness Lz = 1.25L0 is maintained in the pattern, resulting in the lower values of order parameters. It should be noted that the calculations for achievement of steady values of order parameters required a long time as the films become thick, which is demonstrated in Fig. 7b and Fig. S6 of the ESI.†
. The grain boundary of lamellar nanostructures at the film thickness Lz = 1.25L0 is maintained in the pattern, resulting in the lower values of order parameters. It should be noted that the calculations for achievement of steady values of order parameters required a long time as the films become thick, which is demonstrated in Fig. 7b and Fig. S6 of the ESI.†
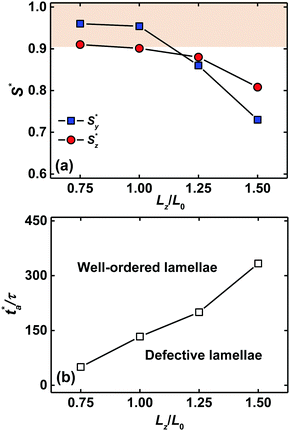
It is important to comprehend the role of the film thickness in the assembly behaviors of block copolymers in the presence of dual fields. Fig. 8a is the plot of steady order parameters Sy* and Sz* in terms of the film thickness at w = 5.0L0 and v = 0.15![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) . In the case of film thickness Lz ≤ 1.00L0, the steady order parameters are both larger than 0.9, implying that the initially defective nanostructures evolve into the well-orientated and well-aligned lamellae via the synergy between the alignment guidance of the chemical template and the imperfection removal of zone annealing. As the film thickness exceeds this range, the steady order parameters have a remarkable reduction, suggesting that the nanostructures of block copolymers retain the metastable configurations.
. In the case of film thickness Lz ≤ 1.00L0, the steady order parameters are both larger than 0.9, implying that the initially defective nanostructures evolve into the well-orientated and well-aligned lamellae via the synergy between the alignment guidance of the chemical template and the imperfection removal of zone annealing. As the film thickness exceeds this range, the steady order parameters have a remarkable reduction, suggesting that the nanostructures of block copolymers retain the metastable configurations.
From Fig. 8a, we can roughly estimate the critical annealing time. Under the condition of film thickness Lz = 1.00L0, the block copolymers are directed to self-assemble into the well-ordered lamellar nanostructures in the presence of zone annealing with width w = 5.0L0 and moving velocity v = 0.15![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) (corresponds to the effective annealing time ta = w/v ≈ 133τ). Decreasing the zone width or increasing the moving velocity leads to the defective nanostructures. Therefore, we can deduce the critical annealing time ta* = 133τ for the film thickness Lz = 1.00L0.
(corresponds to the effective annealing time ta = w/v ≈ 133τ). Decreasing the zone width or increasing the moving velocity leads to the defective nanostructures. Therefore, we can deduce the critical annealing time ta* = 133τ for the film thickness Lz = 1.00L0.
Fig. 8b presents the critical annealing time as a function of the film thickness. It should be mentioned that such a time is also confirmed by the estimated value through changing the parameter settings of zone annealing for a given film thickness (Fig. S7 of the ESI†). In general, the thicker the film of block copolymers is, the longer the effective annealing time becomes. Such a behavior can be understood as follows: in the case of a small value of the film thickness, the block copolymers at the A-attractive stripes are directed to self-assemble into the well-orientated lamellae; thus, these freshly formed nanostructures with a fixed orientation and position act as a soft confinement to program the organization of defective domains as the zone annealing is incorporated into the system. The defects in the soft confined environment are quickly annihilated, leading to the well-ordered nanostructures in a shorter annealing time. However, as the film thickness is increased, the template-guided block copolymers cannot produce the well-oriented lamellae throughout the film. The grain boundaries are observed in the process of zone annealing. To achieve the well-oriented and well-aligned nanostructures, the resident time of block copolymers becomes longer to rearrange themselves (i.e., the cases of lower moving velocity and/or a broader zone width).
Discussion
In previous study, we performed the numerical calculations of the theoretical model in the two-dimensional (2D) space to examine the self-assembly behavior of block copolymers subjected to the dual fields.25 The integrated method allows us to rapidly produce the well-aligned nanostructures under the condition of extremely sparse stripes. From Fig. 2, it is demonstrated that the template-guided block copolymers in conjunction with the zone annealing self-assemble into the well-aligned and well-oriented lamellae at the film thickness Lz = 0.75L0. To further boost the directing efficiency of chemoepitaxy, one can increase the effective annealing time (Fig. 5), which can be tuned by the moving velocity of zone annealing. Therefore, under the condition of ultrathin films of block copolymers, the 3D computational results are generally consistent with the findings of numerical simulations of DSCFT in the 2D space.It should be mentioned that the 2D simulations do not involve the factor of film thickness, which has an important effect on the directing efficiency of chemoepitaxy.63–65 In the present work, the sophisticated model considers the contribution of the film thickness and the corresponding simulations are performed in the 3D boxes with a super-large lateral size. In comparison to the case of 2D simulations, the numerical simulations of DSCFT in the 3D space predict several significant differences (Fig. 6 and 8). Specifically, in the case of ultrathin films, the zone annealing is introduced to align the lamellae along the direction of guiding stripes, which is depicted in Fig. 2. As the film thickness is increased, the zone annealing not only helps the lamellar nanostructures to align along the stripe direction, but also induces the modulation of lamellar orientation via the upward movement of horizontal grain boundaries (Fig. 6 and Fig. S5 of the ESI†). Another distinct difference between the 2D and 3D simulations is that both the film thickness and the effective annealing time have tight relations with the ordering degree of nanostructures. For instance, as the film thickness of block copolymers is increased, the annealing time to yield the well-ordered lamellae becomes long, which is depicted in Fig. 8.
From the experimental perspective, the chemical templates with a sparse arrangement of guiding stripes have an essential consequence for practical applications, because it is not necessary to utilize complicated facilities and techniques to fabricate the prepatterned substrates. As shown in Fig. 5, the extremely sparse stripes have the capability to yield the macroscopically well-ordered nanostructures of block copolymers with the help of zone annealing. The utilization of lower-spatial-frequency templates enhances the throughput of electron-beam lithography. Thus, the sparse stripes used in the integrated method dramatically shorten the electron-beam writing times and lower the fabrication cost of semiconductor devices. In addition, the integrated method is able to produce the well-ordered, standing nanostructures throughout the film in a shorter annealing time. As a consequence, the integrated chemical template/zone annealing method appears as a novel class of directed self-assembly strategy, which is able to rapidly and effectively fabricate the well-ordered nanostructures of block copolymers over a macroscopic area.
Unfortunately, using the synergy between the chemical template and the zone annealing to achieve the defect-free nanostructures has not yet been tested in experiments. However, there still exist some experimental observations regarding the highly ordered nanostructures of block copolymers directed by the dual fields in the literature to support our proposed strategy. For instance, Berry et al. developed a synergistic strategy (i.e., coupling the ordering of the dynamic thermal field with the alignment of the permanent boundary field) to register the alignment of cylindrical nanostructures.42 It was found that the programmable block copolymers inside the graphoepitaxy channels with a wide width are directed to self-assemble into the well-aligned cylinders in a short annealing time. Although the numerical simulations herein are carried out for the case of the integrated chemical template/zone annealing method, Fig. 2 and 6 show an analogous behavior that the defective lamellae guided by the sparse stripes can further evolve into the long-range ordered nanostructures with the help of zone annealing. Therefore, the concept of integrating various directing methods as a synergistic strategy brings us to produce the defect-free patterns over unlimited dimension, even though the templates with sparse motifs are employed.
Finally, it should be pointed out that the local coupling approximation is adopted to describe the collective dynamics of polymer chains in eqn (S4) of the ESI.† In other words, the mobility of polymer chains does not depend on the chain length, and the kinetic coupling between distinct beads is completely neglected. These assumptions may result in the improperly structural evolution of block copolymers. To suitably probe into the kinetics of directed self-assembly of block copolymers, a physically consistent model requires more sophisticated Onsager coefficients via considering the polymer configurations (e.g., the nonlocal coupling models such as Rouse and reptation dynamics consider the influence of chain connectivity).70 Nevertheless, the numerical implementation of collective Rouse or reptation dynamics requires a large sum of computational expense, because of the renewed calculations of the pair-correlation function at every time step. Fortunately, external potential dynamics (EPD) was developed to reduce the computational costs and possesses the essential physical features of nonlocal kinetic coupling.71,72 It was confirmed that the EPD model can capture the formation process of phase-separated structures, especially the case of block copolymers confined between the hard walls. Despite the advantages of EPD, there remains a need for considerable advancements in terms of the noise term through an inverse correlation function, which is difficult to be numerically calculated. After overcoming the challenges, the EPD will provide a feasible method for appropriately describing the directed self-assembly of block copolymers confined between the prepatterned substrate and the air–polymer interface.
Conclusions
In summary, we first report the graphics-processing-unit implementation of dynamic self-consistent field theory for the directed self-assembly of block copolymers in the presence of dual fields of the chemical template and zone annealing. The large-scale simulations enable us to analyze the ordering degree of nanostructures over a large area. Using the numerical simulations, we corroborate the results that the integrated chemical template/zone annealing method has the capability to rapidly fabricate the well-aligned and well-oriented nanostructures over a macroscopic area, even though the underlying stripes are extremely sparse or the film thickness becomes thick. Furthermore, the effective annealing time to achieve the well-ordered nanostructures has tight relationships with the pitch of the guiding stripes and the thickness of films.Conflicts of interest
We declare that we have no conflict of interest.Acknowledgements
This work was supported by the National Natural Science Foundation of China (21574040 and 21234002).References
- J. Y. Cheng, A. M. Mayes and C. A. Ross, Nat. Mater., 2004, 3, 823–828 CrossRef CAS PubMed.
- J. Y. Cheng, C. A. Ross, H. I. Smith and E. L. Thomas, Adv. Mater., 2006, 18, 2505–2521 CrossRef CAS.
- R. A. Segalman, Mater. Sci. Eng., R, 2005, 48, 191–226 CrossRef.
- M. Luo and T. H. Epps III, Macromolecules, 2013, 46, 7567–7579 CrossRef CAS.
- C. M. Bates, M. J. Maher, D. W. Janes, C. J. Ellison and C. G. Willson, Macromolecules, 2014, 47, 2–12 CrossRef CAS.
- T. R. Albrecht, H. Arora, V. Ayanoor-Vitikkate and E. Yang, IEEE Trans. Magn., 2015, 51, 0800342 CrossRef.
- J. Chai and J. M. Buriak, ACS Nano, 2008, 2, 489–501 CrossRef CAS PubMed.
- C. M. Bates and F. S. Bates, Macromolecules, 2017, 50, 3–22 CrossRef CAS.
- M. P. Stoykovich, M. Müller, S. O. Kim, H. H. Solak, E. W. Edwards, J. J. de Pablo and P. F. Nealey, Science, 2005, 308, 1442–1446 CrossRef CAS PubMed.
- R. Ruiz, H. Kang, F. A. Detcheverry, E. Dobisz, D. S. Kercher, T. R. Albrecht, J. J. de Pablo and P. F. Nealey, Science, 2008, 321, 936–939 CrossRef CAS PubMed.
- K. Koo, H. Ahn, S.-W. Kim, D. Y. Ryu and T. P. Russel, Soft Matter, 2013, 9, 9059–9071 RSC.
- C. G. Hardy and C. Tang, J. Polym. Sci., Part B: Polym. Phys., 2013, 51, 2–15 CrossRef CAS.
- K. G. A. Tavakkoli, K. W. Gotrik, A. F. Hannon, A. Alexander-Katz, C. A. Ross and K. K. Berggren, Science, 2012, 336, 1294–1298 CrossRef CAS PubMed.
- M. Fernández-Regúlez, L. Evangelio, M. Lorenzoni, J. Fraxedas and F. Pérez-Murano, ACS Appl. Mater. Interfaces, 2014, 6, 21596–21602 Search PubMed.
- S. P. Samant, C. A. Grabowski, K. Kisslinger, K. G. Yager, G. Yuan, S. K. Satija, M. F. Durstock, D. Raghavan and A. Karim, ACS Appl. Mater. Interfaces, 2016, 8, 7966–7976 CAS.
- L. Rockford, Y. Liu, P. Mansky, T. P. Russell, M. Yoon and S. G. J. Mochrie, Phys. Rev. Lett., 1999, 82, 2602–2605 CrossRef CAS.
- S. O. Kim, H. H. Solak, M. P. Stoykovich, N. J. Ferrier, J. J. de Pablo and P. F. Nealey, Nature, 2003, 424, 411–414 CrossRef CAS PubMed.
- E. W. Edwards, M. P. Stoykovich, H. H. Solak and P. F. Nealey, Macromolecules, 2006, 39, 3598–3607 CrossRef CAS.
- J. Y. Cheng, C. T. Rettner, D. P. Sanders, H.-C. Kim and W. D. Hinsberg, Adv. Mater., 2008, 20, 3155–3158 CrossRef CAS.
- Y. Tada, S. Akasaka, M. Takenaka, H. Yoshida, R. Ruiz, E. Dobisz and H. Hasegawa, Polymer, 2009, 50, 4250–4256 CrossRef CAS.
- M. J. Maher, C. T. Rettner, C. M. Bates, G. Blachut, M. C. Carlson, W. J. Durand, C. J. Ellison, D. P. Sanders, J. Y. Cheng and C. G. Willson, ACS Appl. Mater. Interfaces, 2015, 7, 3323–3328 CAS.
- H. S. Suh, D. H. Kim, P. Moni, S. Xiong, L. E. Ocola, N. J. Zaluzec, K. K. Gleason and P. F. Nealey, Nat. Nanotechnol., 2017, 12, 575–581 CrossRef CAS PubMed.
- W. Li, F. Qiu, Y. Yang and A.-C. Shi, Macromolecules, 2010, 43, 1644–1650 CrossRef CAS.
- H. Deng, N. Xie, W. Li, F. Qiu and A.-C. Shi, Macromolecules, 2015, 48, 4174–4182 CrossRef CAS.
- X. Wan, T. Gao, L. Zhang and J. Lin, Phys. Chem. Chem. Phys., 2017, 19, 6707–6720 RSC.
- Z. Qiang, L. Zhang, G. E. Stein, K. A. Cavicchi and B. D. Vogt, Macromolecules, 2014, 47, 1109–1116 CrossRef CAS.
- S. Y. Kim, A. Nunns, J. Gwyther, R. L. Davis, I. Manners, P. M. Chaikin and R. A. Register, Nano Lett., 2014, 14, 5698–5705 CrossRef CAS PubMed.
- C. Liedel, C. W. Pester, M. Ruppel, V. S. Urban and A. Böker, Macromol. Chem. Phys., 2012, 213, 259–269 CrossRef CAS.
- T. Hashimoto, J. Bodycomb, Y. Funaki and K. Kimishima, Macromolecules, 1999, 32, 952–954 CrossRef CAS.
- K. Mita, H. Tanaka, K. Saijo, M. Takenaka and T. Hashimoto, Macromolecules, 2007, 40, 5923–5933 CrossRef CAS.
- D. E. Angelescu, J. H. Waller, D. H. Adamson, R. A. Register and P. M. Chaikin, Adv. Mater., 2007, 19, 2687–2690 CrossRef CAS.
- B. C. Berry, A. W. Bosse, J. F. Douglas, R. L. Jones and A. Karim, Nano Lett., 2007, 7, 2789–2794 CrossRef CAS PubMed.
- G. Singh, K. G. Yager, B. Berry, H.-C. Kim and A. Karim, ACS Nano, 2012, 6, 10335–10342 CrossRef CAS PubMed.
- G. Singh, K. G. Yager, D.-M. Smilgies, M. M. Kulkarni, D. G. Bucknall and A. Karim, Macromolecules, 2012, 45, 7107–7117 CrossRef CAS.
- P. W. Majewski and K. G. Yager, ACS Nano, 2015, 9, 3896–3906 CrossRef CAS PubMed.
- P. W. Majewski and K. G. Yager, J. Phys.: Condens. Matter, 2016, 28, 403002 CrossRef PubMed.
- P. W. Majewski and K. G. Yager, Nano Lett., 2015, 15, 5221–5228 CrossRef CAS PubMed.
- A. G. Jacobs, C. Liedel, H. Peng, L. Wang, D.-M. Smilgies, C. K. Ober and M. O. Thompson, Macromolecules, 2016, 49, 6462–6470 CrossRef CAS.
- H. M. Jin, S. H. Lee, J. Y. Kim, S. W. Son, B. H. Kim, H. K. Lee, J. H. Mun, S. K. Cha, J. S. Kim and P. F. Nealey, ACS Nano, 2016, 10, 3435–3442 CrossRef CAS PubMed.
- U. Welling and M. Müller, Soft Matter, 2017, 13, 486–495 RSC.
- J. D. Hill and P. C. Millett, Sci. Rep., 2017, 7, 5250 CrossRef PubMed.
- B. C. Berry, G. Singh, H.-C. Kim and A. Karim, ACS Macro Lett., 2013, 2, 346–350 CrossRef CAS.
- C. C. Kathrein, W. Bai, J. A. Currivan-Incorvia, G. Liontos, K. Ntetsikas, A. Avgeropoulos, A. Böker, L. Tsarkova and C. A. Ross, Chem. Mater., 2015, 27, 6890–6898 CrossRef CAS.
- D. Borah, M. T. Shaw, J. D. Holmes and M. A. Morris, ACS Appl. Mater. Interfaces, 2013, 5, 2004–2012 CAS.
- X. Zhang, J. N. Murphy, N. L. Y. Wu, K. D. Harris and J. M. Buriak, Macromolecules, 2011, 44, 9752–9757 CrossRef CAS.
- L. Wan, S. Ji, C.-C. Liu, G. S. W. Craig and P. F. Nealey, Soft Matter, 2016, 12, 2914–2922 RSC.
- C. Simão, W. Khunsin, N. Kehagias, M. Salaun, M. Zelsmann, M. A. Morris and C. M. S. Torres, Nanotechnology, 2014, 25, 175703 CrossRef PubMed.
- Z. Qiang, Y. Zhang, J. A. Groff, K. A. Cavicchi and B. D. Vogt, Soft Matter, 2014, 10, 6068–6076 RSC.
- G. Blachut, S. M. Sirard, M. J. Maher, Y. Asano, Y. Someya, A. P. Lane, W. J. Durand, C. M. Bates, A. M. Dinhobl, R. Gronheid, D. Hymes, C. J. Ellison and C. G. Willson, Chem. Mater., 2016, 28, 8951–8961 CrossRef CAS.
- T. Segal-Peretz, J. Ren, S. Xiong, G. Khaira, A. Bowen, L. E. Ocola, R. Divan, M. Doxastakis, N. J. Ferrier, J. J. de Pablo and P. F. Nealey, ACS Nano, 2017, 11, 1307–1319 CrossRef CAS PubMed.
- J. G. E. M. Fraaije, B. A. C. van Vlimmeren, N. M. Maurits, M. Postma, O. A. Evers, C. Hoffmann, P. Altevogt and G. Goldbeck-Wood, J. Chem. Phys., 1997, 106, 4260–4269 CrossRef CAS.
- L. Zhang, L. Wang and J. Lin, ACS Macro Lett., 2014, 3, 712–716 CrossRef CAS.
- G. H. Fredrickson, The Equilibrium Theory of Inhomogeneous Polymers, Oxford University Press, Oxford, 2006 Search PubMed.
- B. A. C. van Vlimmeren and J. G. E. M. Fraaije, Comput. Phys. Commun., 1996, 99, 21–28 CrossRef CAS.
- H. Furukawa, Physica A, 1992, 180, 128–155 CrossRef CAS.
- H. D. Zhang, J. Zhang, Y. Yang and X. Zhou, J. Chem. Phys., 1997, 106, 784–792 CrossRef CAS.
- A. W. Bosse, J. F. Douglas, B. C. Berry, R. L. Jones and A. Karim, Phys. Rev. Lett., 2007, 99, 216101 CrossRef PubMed.
- Z. Cong, L. Zhang, L. Wang and J. Lin, J. Chem. Phys., 2016, 144, 114901 CrossRef PubMed.
- F. A. Detcheverry, G. Liu, P. F. Nealey and J. J. de Pablo, Macromolecules, 2010, 43, 3446–3454 CrossRef CAS.
- C.-C. Liu, A. Ram, E. Han, G. S. W. Craig, Y. Tada and P. F. Nealey, Macromolecules, 2013, 46, 1415–1424 CrossRef CAS.
- L. Zhang, A. Sevink and F. Schmid, Macromolecules, 2011, 44, 9434–9447 CrossRef CAS.
- X. Cao, L. Zhang, L. Wang and J. Lin, Soft Matter, 2014, 10, 5916–5927 RSC.
- V. Mishra, G. H. Fredrickson and E. J. Kramer, ACS Nano, 2012, 6, 2629–2641 CrossRef CAS PubMed.
- F. F. Lupi, T. J. Giammaria, G. Seguini, M. Laus, P. Dubček, B. Pivac, S. Bernstorff and M. Perego, ACS Appl. Mater. Interfaces, 2017, 9, 11054–11063 Search PubMed.
- C. T. Black, C. Forrey and K. G. Yager, Soft Matter, 2017, 13, 3275–3283 RSC.
- W. Li, P. F. Nealey, J. J. de Pablo and M. Müller, Phys. Rev. Lett., 2014, 113, 168301 CrossRef PubMed.
- O. Kuksenok, R. D. M. Travasso and A. C. Balazs, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2006, 74, 011502 CrossRef PubMed.
- E. W. Edwards, M. P. Stoykovich, M. Müller, H. H. Solak, J. J. de Pablo and P. F. Nealey, J. Polym. Sci., Part B: Polym. Phys., 2005, 43, 3444–3459 CrossRef CAS.
- A. M. Welander, G. S. W. Craig, Y. Tada, H. Yoshida and P. F. Nealey, Macromolecules, 2013, 46, 3915–3921 CrossRef CAS.
- M. Doi and S. F. Edwards, The Theory of Polymer Dynamics, Clarendon Press, Oxford, 1986 Search PubMed.
- N. M. Maurits and J. G. E. M. Fraaije, J. Chem. Phys., 1997, 107, 5879–5889 CrossRef CAS.
- E. Reister and M. Müller, J. Chem. Phys., 2003, 118, 8476–8488 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c7cp06261c |
| This journal is © the Owner Societies 2018 |