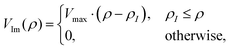3D time-dependent wave-packet approach in hyperspherical coordinates for the H + O2 reaction on the CHIPR and DMBE IV potential energy surfaces†
Received
13th September 2017
, Accepted 28th November 2017
First published on 28th November 2017
Abstract
We perform quantum dynamics calculations for the reaction H + O2 → O + OH on the ground-state potential energy surfaces CHIPR [Varandas, J. Chem. Phys., 2013, 138, 134117] and DMBE IV [Pastrana et al., J. Phys. Chem. 1990, 94, 8073] using a three-dimensional time-dependent wave packet formalism based on hyperspherical coordinates. Initial rovibrational state [O2(v = 0–4, j = 1–5)] dependent reaction probabilities are calculated for the case J = 0. The J-shifting scheme is employed to estimate initial state selected integral cross-sections as well as thermal rate coefficients, which is verified using a realistic extrapolation scheme. The calculated total and state-to-state rate coefficients are compared with the findings of recent experimental studies and previous theoretical calculations.
1 Introduction
An accurate formalism for solving triatomic reactive scattering on a single Born–Oppenheimer (BO) PES was attempted a while ago by Kuppermann, Schatz and Baer.1 A while later, several theoretical investigations2–5 and experimental advances6–9 were reported to calculate rovibrationally resolved cross sections. Further developments of both time-independent (TI) and time-dependent (TD) methodologies10,11 also appeared to illustrate those experimental findings. With the formulation of a TD wave packet approach for triatomic reactive scattering initially performed in Jacobi coordinates,12,13 Zhang and co-workers14 and later Kouri and co-workers15 implemented the “reactants–products decoupling” (RPD) scheme to overcome the reactants–products coordinate transformation.
The development of an accurate quantum dynamics algorithm16–18 led to the evaluation of accurate integrals and differential cross-sections for atom–diatom collision processes. Various TD quantum mechanical approaches then appeared to assess reaction probabilities for a variety of reactive systems.19–21 On the other hand, the Coupled Channel (CC) approach in hyperspherical coordinates22–26 removed the awkward problem of coordinate transformation from the reactants to the products channel and made the formulation convenient for an equivalent description of all the rearrangement channels. Moreover, the extension of a reactive scattering calculation in hyperspherical coordinates on multiple electronic states for non-zero total angular momentum is straightforward to implement numerically rather than the traditional Jacobi coordinate system. The computational cost of such a CC approach scales as (JΠNi)3, with the use of the grid method reducing the cost to 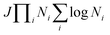 , where J is the total angular momentum and Ni is the number of basis functions for the ith internal coordinate. Billing and Markovic25 formulated such a four-dimensional (4D) quantum mechanical problem of triatomic reactive scattering using hyperspherical coordinates and performed calculations for the D + H2 system in the simplest cases of J = 0, and J = 1. This approach was further transmuted by Adhikari and Varandas22 for the extension to higher J ≠ 0 situations. The state-to-state as well as total cross sections and rate coefficients have been accurately calculated by Adhikari and coworkers via the implementation of an OpenMP-MPI parallelized algorithm for the TD wave packet approach to the D+ + H2 system using both the lowest adiabatic singlet sheet (11A′)23,24 and lowest three singlet sheets (11A′, 21A′ and 31A′)27 of the double many-body expansion (DMBE) PES for H3+ reported by Varandas and coworkers.28 The results were found to be in good agreement with experimental observations29–31 and previous theoretical calculations.32,33 Very recently, Adhikari and coworkers34 constructed accurate diabatic potential energy surfaces for the lowest three singlet states of H3+
, where J is the total angular momentum and Ni is the number of basis functions for the ith internal coordinate. Billing and Markovic25 formulated such a four-dimensional (4D) quantum mechanical problem of triatomic reactive scattering using hyperspherical coordinates and performed calculations for the D + H2 system in the simplest cases of J = 0, and J = 1. This approach was further transmuted by Adhikari and Varandas22 for the extension to higher J ≠ 0 situations. The state-to-state as well as total cross sections and rate coefficients have been accurately calculated by Adhikari and coworkers via the implementation of an OpenMP-MPI parallelized algorithm for the TD wave packet approach to the D+ + H2 system using both the lowest adiabatic singlet sheet (11A′)23,24 and lowest three singlet sheets (11A′, 21A′ and 31A′)27 of the double many-body expansion (DMBE) PES for H3+ reported by Varandas and coworkers.28 The results were found to be in good agreement with experimental observations29–31 and previous theoretical calculations.32,33 Very recently, Adhikari and coworkers34 constructed accurate diabatic potential energy surfaces for the lowest three singlet states of H3+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 35 using first principle-based beyond Born–Oppenheimer theory36 and performed quantum dynamics using this hyperspherical coordinate-based scattering code on those surfaces to calculate state-to-state integral cross sections and found an overwhelming agreement with most recent available experimental data for all three competing charge transfer channels. In a similar context, Adhikari, Varandas and coworkers employed the same methodology for the O + OH reaction37 using both the (combined-hyperbolic-inverse-power-representation) CHIPR38 and DMBE IV PESs39 of HO2 and the J-shifting approximation to calculate state-to-state thermal rate coefficients. Moreover, 3D as well as coupled 3D time-dependent wave packet approaches have been employed for several other triatomic reactions in Jacobi coordinates, viz., F + H2,40,41 O(1D) + N2,42 H + D2,43 O + H2,44 D + H2 and H + D245etc. and in hyperspherical coordinates, viz., D + H2,22,25 D+ + H2,23,24,27,34,46 F + H2,47etc. On the other hand, going beyond the atom–diatom to polyatomic reactive scattering is a big challenge in quantum dynamics, since the major bottleneck is to handle the exponential increase in computational cost due to the increase in mathematical dimensionalities when the number of atoms involved in the collision increases from three to four. For example, the dimensionality in terms of internal degrees of freedom increases from three for a triatomic system to six for a tetra-atomic system. On the contrary, the main computational advantage of a time-dependent approach is its smaller computational scaling with the number of basis functions (≤N2vs. N3 in the standard CC time-independent method). Owing to its favorable computational scaling, the time-dependent approach is preferred for some large-scale computational tasks for various large molecules in reaction dynamics. In addition to that, utilization of hyperspherical coordinates is advantageous as it is able to handle all the reactant and product channels evenhandedly. To summarize, the rigorous dynamical treatment for tetra-atomic reactions is still not performed in hyperspherical coordinates, although a few calculations have been reported by using the time-dependent wave packet methodology in Jacobi coordinates for various tetra-atomic reactions, viz. H + H2O,48–51 H + H2S,52 H + CO2,53 OH + D254etc.
35 using first principle-based beyond Born–Oppenheimer theory36 and performed quantum dynamics using this hyperspherical coordinate-based scattering code on those surfaces to calculate state-to-state integral cross sections and found an overwhelming agreement with most recent available experimental data for all three competing charge transfer channels. In a similar context, Adhikari, Varandas and coworkers employed the same methodology for the O + OH reaction37 using both the (combined-hyperbolic-inverse-power-representation) CHIPR38 and DMBE IV PESs39 of HO2 and the J-shifting approximation to calculate state-to-state thermal rate coefficients. Moreover, 3D as well as coupled 3D time-dependent wave packet approaches have been employed for several other triatomic reactions in Jacobi coordinates, viz., F + H2,40,41 O(1D) + N2,42 H + D2,43 O + H2,44 D + H2 and H + D245etc. and in hyperspherical coordinates, viz., D + H2,22,25 D+ + H2,23,24,27,34,46 F + H2,47etc. On the other hand, going beyond the atom–diatom to polyatomic reactive scattering is a big challenge in quantum dynamics, since the major bottleneck is to handle the exponential increase in computational cost due to the increase in mathematical dimensionalities when the number of atoms involved in the collision increases from three to four. For example, the dimensionality in terms of internal degrees of freedom increases from three for a triatomic system to six for a tetra-atomic system. On the contrary, the main computational advantage of a time-dependent approach is its smaller computational scaling with the number of basis functions (≤N2vs. N3 in the standard CC time-independent method). Owing to its favorable computational scaling, the time-dependent approach is preferred for some large-scale computational tasks for various large molecules in reaction dynamics. In addition to that, utilization of hyperspherical coordinates is advantageous as it is able to handle all the reactant and product channels evenhandedly. To summarize, the rigorous dynamical treatment for tetra-atomic reactions is still not performed in hyperspherical coordinates, although a few calculations have been reported by using the time-dependent wave packet methodology in Jacobi coordinates for various tetra-atomic reactions, viz. H + H2O,48–51 H + H2S,52 H + CO2,53 OH + D254etc.
The reaction between H(2S) and O2(3Σ−g) is one of the most important elementary reactions in combustion chemistry. It is considered to be the rate-determining step in the combustion of hydrogen and hydrocarbons, and consumes ∼80% of O2 producing hydrocarbon-air flames in the atmosphere.55 Moreover, the title reaction is considered to be a prototype for complex-forming chemical reactions.56 Owing to such important attributes, many electronic structure calculations have been performed to construct a potential energy surface (PES) for the title system, and thereafter reactive scattering calculations are carried out to obtain temperature-dependent rate coefficients. Consequently, a kinetics study of accurate rate coefficients for the title reaction is highly demanding. Recall that the reverse reaction is also very important in interstellar chemistry, where it has a primary role in the destruction of ozone.
Numerous experimental measurements of the rate coefficient for the title reaction have been accomplished. Cohen and Westberg57 in 1983 reported a rate constant for the temperature range 250–2000 K. Later on, Baulch et al.58 obtained rate coefficients for various combustion processes including the title reaction, and Warnatz59 accumulated data for the same reaction. In turn, Shin and Michael60 carried out experiments by employing a laser photolysis-shock tube technique to check the rate constant in the temperature range 1103 ≤ T/K ≤ 2055, which were the first direct rate constant measurements in such a high temperature range. Owing to the endothermic nature of the reaction, the temperature-dependent rate constant is found to be Arrhenius in nature. To have a complete understanding of the reaction mechanism, several theoretical calculations have been performed to construct the potential energy surface with different levels of accuracy. Several versions of the electronically adiabatic PES have been reported, starting with Melius and Blint61 (MB). Subsequently, Pastrana et al.39 reported the DMBE IV surface by using dynamical simulations. In turn, Kendrick and Pack62 reported a diatomics-in-molecules type (DIMKP) PES. There are other available forms of ab initio surfaces by Troe and Ushakov (TU)63 and XXZLG PES of Xu et al.64,65 For the present calculations, we have employed the CHIPR38 PES, the most recent and likely accurate PES for the title system, which utilizes ab initio data from the XXZLG PES64 and the CHIPR method of Varandas.66 Dynamical calculations on the popular DMBE IV PES39 are also reported.
On the computational side, a large number of quantum dynamics studies have been carried out for the title reaction. Recently, Teixidor and Varandas employed the CHIPR38 PES of HO2 for dynamics calculations with the ABC time-independent quantum scattering program based on hyperspherical coordinates. They were able to evaluate thermal rate constants by the J-shifting technique,67 which were compared with the theoretical calculations68 on XXZLG and DIMKP PESs as well as experimental findings.57–59 The same authors reported similar calculations69 on the CHIPR PES for the X + O2 reactive system, with X being atomic hydrogen isotopes (Mu, H, D and T). Previously, Varandas70,71 utilized the trajectory calculations on the DMBE IV PES and calculated the thermal rate coefficients for the title reaction via an extrapolation method,70 whereas Pack et al.72,73 performed a TI quantum dynamics study on the same PES using the adiabatically adjusting principal-axis hyperspherical coordinates (APH) method. In turn, Duchovic et al. studied the H + O2 reaction on the MB and DMBE IV PESs by using quasiclassical trajectory (QCT) calculations.74 A while later, Lin et al.75 calculated the state-to-state reaction probabilities of the same reaction on the XXZLG PES with time-independent as well as time-dependent quantum mechanical methods. Moreover, the title reaction was extensively investigated by Bergueno et al.76 using time-dependent wave packet (TDWP) and statistical methods to calculate reaction probabilities and integral cross sections. Additionally, Guo and coworkers77 employed a fully Coriolis coupled time-dependent quantum mechanical methodology to calculate reaction probabilities for J ≠ 0 situations, whereas Sun et al.78 predicted the nonstatistical nature of the reaction. On the other hand, the effect of initial rotational state excitation on the reactivity of the title reaction has been studied by Guo, Lendvay and coworkers79 by utilizing the statistical phase space theory, the QCT method and the quantum wave packet approach. In turn, Viel et al.80 utilized a Lanczos formalism based on Green′s function and the DMBE IV PES to obtain J = 0 reaction probabilities and then, the J-shifting approach to calculate thermal rate coefficients. Meijer and Goldfield,81–83 in a series of studies using TD quantum mechanics with body fixed (BF) Jacobi coordinates on the DMBE IV PES, reported total reaction probabilities and cross sections for J = 0 and J > 0 situations, which highlighted the importance of the close-coupling approach. In turn, Sultanov and Balakrishnan84 performed TI quantum calculations on both DMBE IV and TU PESs for computing J = 0 cumulative reaction probabilities and thereafter J-shifted rate coefficients. A while later, Lin and coworkers,85 performed both the TD and TI quantum dynamics calculations on the XXZLG and DMBE IV PESs, whereas Hankel et al.86 calculated reaction probabilities for both the J = 0 and J > 0 situations by using a TD quantum method and the DMBE IV, TU and XXZLG PESs. In turn, Honvault et al.87 presented both the differential and integral cross sections for non-zero total angular momenta up to 50. Moreover, Quéméner et al.68 performed quantum dynamics calculations on the XXZLG and DIMKP PESs to study the initial rovibrational excitation of the reactant O2 molecule on the state-to-state reaction probabilities as well as J-shifted rate coefficients, and compared the calculated integral cross sections with available experimental measurements.88–90
To summarize, we have investigated the following reaction for the formation of OH(2Π):
| H(2S) + O2(3Σ−g) → OH(2Π) + O(3P), |
with dynamics calculations carried out on both the adiabatic CHIPR
38 and DMBE IV PESs
39 of HO
2 to explore the workability of our TD wave packet approach
22–24,27 by using Bowman's
J-shifting technique
67 and the extrapolation method of Varandas
70 in the collision energy range 0.0–2.6 eV. Initial state selected integral cross sections and rate coefficients are computed and compared with previous theoretical calculations and available experimental findings.
2 Theoretical background
The initial wave packet in hyperspherical coordinates can be expressed in terms of the 3-j symbol and modified spherical harmonics (Cjμ):| | 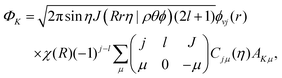 | (1) |
where| | 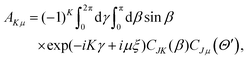 | (2) |
with the hyperradius ρ and two hyperangles θ and ϕ being the three internal coordinates of the hyperspherical coordinate system, which define the geometry of the ABC triatomic plane. On the other hand, the orientation of the plane is monitored by the three external coordinates, the Euler angles α, β and γ. The expressions for the other angles Θ′ and ξ are given in terms of the Euler angles as:22which define the orientation of R and r in the space-fixed and body-fixed coordinate systems, respectively.
Moreover, AKμ obeys the orthonormality condition,
| | 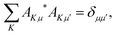 | (5) |
and finally, the
K-component wave is normalized as
| | 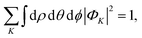 | (6) |
ϕ
vj
(r) is a diatomic Morse wave function, χ(R) is the translational wave function corresponding to the A + BC relative motion, and J(Rrη|ρθϕ) is the Jacobian for the transformation from Jacobi to hyperspherical coordinates.22,23
The Hamiltonian operator describing the three-particle system can be written in terms of Johnson's hypersherical coordinates:91
| | 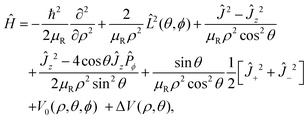 | (7) |
where
V0(
ρ,
θ,
ϕ) is the potential as a function of internal coordinates
ρ,
θ and
ϕ,
Ĵ+2 and
Ĵ−2 are raising and lowering operators, respectively and all other operators are discussed elaborately elsewhere.
22
Upon substituting the wave packet and the Hamiltonian into the TD Schrödinger equation (TDSE), the following set of coupled equations can be obtained:
| | 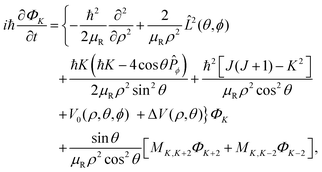 | (8) |
where the
K-component waves
ΦK and
ΦK±2 are coupled
via the coupling element:
| | 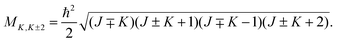 | (9) |
Projection of the TD wave packet on the asymptotic eigenstates at a fixed value of
R(=
R*) is carried out to greatly simplify the propagation,
25,92 where the couplings among the channels are assumed to be negligible. Thus, the scattering amplitudes in the various channels for
v′,
j′,
l′ can be obtained as:
| | 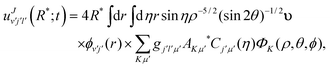 | (10) |
where
gjlμ is the Clebsch–Gordon coefficient defined as
23| | 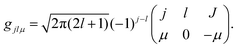 | (11) |
The above integration is carried out over the (
θ,
ϕ) grid using the relations:
| | 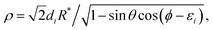 | (12) |
| | 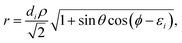 | (13) |
| | 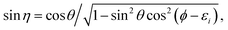 | (14) |
with the Jacobi factor (for fixed
R) defined as:
| | 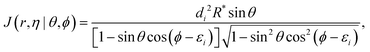 | (15) |
where
di and
εi are channel-dependent constants. In order to have the values of
ΦK on the (
θ,
ϕ)-space at
R =
R*, we interpolate the amplitudes of
ΦKs on the grid values.
When the wave packet passes through the projection region and gets almost absorbed at the boundary, the scattering amplitudes are Fourier transformed from time to energy space:
| | 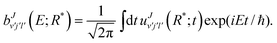 | (16) |
Those amplitudes are expanded in terms of incoming and outgoing waves as:
| | 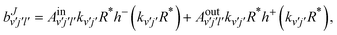 | (17) |
where
| | | h±(kv′j′R*) = −nl(kv′j′R*) ± ijl(kv′j′R*), | (18) |
and
jl and
nl are the spherical Bessel and Neumann functions, respectively. Since the projection on the incoming component of the scattering amplitude should be zero, the reaction probability from the initial state (
vjl) to the product state (
v′
j′
l′) could be calculated as the ratio of the outgoing and incoming fluxes,
| | 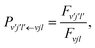 | (19) |
where
| | 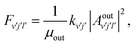 | (20) |
| | 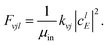 | (21) |
The scattering amplitude of the initial wave packet at energy
E is denoted as
clE.
kvj and
kv′j′ are the wave numbers of the initial (
vj) and final (
v′
j′) channels, respectively.
μin and
μout are the appropriate centers of masses for the reactants and products, respectively. The weight in energy space is related to the weight in
k space through the relation:
| | 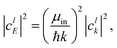 | (22) |
where the analytic expression for |
clk|
2 can be obtained for a Gaussian wave packet as:
| | 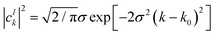 | (23) |
with
σ being the width of the Gaussian wave packet. This expression is valid only for a free particle that corresponds to a system initialized at very large separation.
The initial state selected cross sections by J-shifting can be obtained as:68
| | 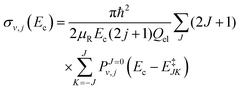 | (24) |
where
μR is the reduced mass for the reactant channel,
Ec is the collision energy and
Qel = 3. The rotational energy,
E‡JK, at the transition state for a symmetric top geometry is given by:
| | | E‡JK = B‡J(J + 1) + (A‡ − B‡)K2, | (25) |
where
A‡ and
B‡ are rotational constants [see Table S1 of the ESI
†] considering a symmetric top geometry of the O⋯OH transition state complex. It may be noted that the values of
A‡ and
B‡ differ for different PESs employed in the dynamical calculation as depicted elsewhere.
93
The thermal rate coefficient can be calculated by simply applying the J-shifting approximation as:
| | 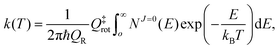 | (26) |
where
QR =
QelQtransQrot-vib is the partition function per unit of volume of the reactants and
NJ=0(
E) is the cumulative reaction probability defined as:
| | 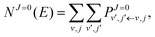 | (27) |
and the other partition functions are defined as:
| | 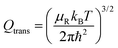 | (28) |
| | 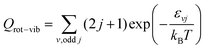 | (29) |
| | 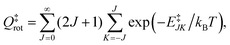 | (30) |
where
εvj are the O
2 rovibrational energies.
On the other hand, considering the general form of the integral cross section,
| | 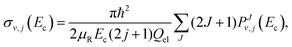 | (31) |
and following an extrapolation procedure proposed by one of us,
70 we approximate the reaction probability for the
Jth case by
| | 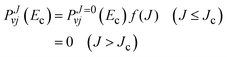 | (32) |
where
f(
J) is a model distribution function of the form
| | 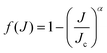 | (33) |
with
α and
Jc (cutoff of total angular momentum) being suitable parameters. This allows us to evaluate the summation in
eqn (31) by using the Euler–MacLaurin formula. For a quadratic-
J distribution (
i.e.,
α = 2), the expression for
σv,j becomes
| | 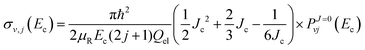 | (34) |
Using the above quadratic-
J distribution,
Jc was predicted
70 to be ∼57 for the DMBE IV PES. Given the similarity of the DMBE IV and CHIPR PESs, we use later the same set of parameters to check the accuracy of the presently employed
J-shifting approximation.
2.1 The absorbing potential
A negative imaginary potential at the last few grid points for the hyperradius at each θ and ϕ is plugged in to remove the unphysical reflections from the grids. Thus, the total potential of the system can be written as| | | V(ρ,θ,ϕ) = V0(ρ,θ,ϕ) − iVIm(ρ). | (35) |
We have used a linear absorbing potential46,94 of the following form:
where ρI is the starting point for such a potential with Vmax monitoring minimal reflection of the wave function from the boundary. The various numerical parameters are tabulated in Table S1 of the ESI.†
2.2 Propagation, projection and computation details
The kinetic energy operators are evaluated by the Fast Fourier Transformation (FFT)95 method which can scale the computational cost as cN![[thin space (1/6-em)]](https://www.rsc.org/images/entities/i_char_2009.gif) log
log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/i_char_2009.gif) N, with N being the total number of grid points on the ρ, θ and ϕ coordinates. Time propagation of the wave packet is monitored by the iterative Lanczos reduction technique, which is basically a short time propagator. The demand of huge computational cost is illustrated elsewhere22,23 with the detailed discussion about the implementation of the OpenMP-MPI parallelization scheme.23,27
N, with N being the total number of grid points on the ρ, θ and ϕ coordinates. Time propagation of the wave packet is monitored by the iterative Lanczos reduction technique, which is basically a short time propagator. The demand of huge computational cost is illustrated elsewhere22,23 with the detailed discussion about the implementation of the OpenMP-MPI parallelization scheme.23,27
3 Results and discussion
We have performed TD 3D wave packet dynamics in hyperspherical coordinates for the H + O2 reaction employing both the CHIPR66 and DMBE IV39 PESs for HO2. Specifically, reaction probabilities are calculated for product formation (O + OH) with zero total angular momentum and thereafter, the J-shifting approximation67 is employed to calculate integral cross sections and temperature-dependent rate coefficients, which are here verified using Varandas' extrapolation scheme.70
Panel-(a) of Fig. 1 depicts the total reaction probabilities calculated as a function of collision energy for the reaction H + O2(v = 0; j = 1) → OH(v′,j′) + O at J = 0 performed on the adiabatic CHIPR PES, whereas panel-(b) displays the same, but on the DMBE IV PES. In panel-(b), the previous time-dependent quantum mechanical calculations on the DMBE IV PES for the reaction probability at J = 0 are shown over the collision energy range 0.0–1.8 eV by Hankel and coworkers86 and Abu Bajeh et al.89 While comparing the results from the CHIPR PES with DMBE IV, all the reaction profiles are seen to be in close agreement except some apparent differences due to resonances. Specifically, the CHIPR reaction probability profile shows a threshold value close to ∼0.67 eV, and gradually acquires higher values from there onwards, a pattern also consistent with the previous calculations performed on the DMBE IV PES. The existence of such a threshold value is due to the appearance of an effective barrier in the exit channel which corresponds to the opening of the OH(v′,j′) + O products channel. Note also the fact that the magnitude of the profile for the DMBE IV case is in good accordance with the previous theoretical calculations86,89 except for some peaks and troughs of the profiles up to ∼1.8 eV; after a collision energy of ∼2.0 eV, the present profile tends to slightly decrease. On the other hand, Fig. 2 depicts the calculated cumulative reaction probability (CRP) on the CHIPR PES for the H + O2 reaction as a function of total energy due to all possible initial rovibrational states of the reactant, O2. Also included for comparison in this plot are the results extracted from the time-independent quantum scattering calculations of Quéméner et al.68 on the DIMKP PES (magenta curve) and the results of Teixidor and Varandas93 on the CHIPR PES (blue curve). It may be noted that we have calculated the CRP by involving reaction probabilities for all the initial rovibrational states (v, j) of an O2 diatom as well as all the final rovibrational states (v′, j′) of the OH diatom considered in our calculation [see Table 1], where the state-to-state reaction probability profiles at various collision energies are well converged with respect to final rotational (j′) as well as final vibrational (v′) quantum numbers. Additionally, the convergence profiles for state-to-state reaction probabilities at four different collision energies, viz., Ec = 0.50 eV, 1.0 eV, 1.5 eV and 2.0 eV are depicted in the ESI,† which clearly indicate that the reaction probability profiles are gradually converging as j′ increases from 0 to 15 and v′ increases from 0 to 10. It is quite noteworthy that the trends of the other theoretical profiles obtained from the DIMKP and CHIPR PESs are quite similar to the presently calculated one on the CHIPR PES. Indeed, despite some mismatch in the magnitudes of different profiles, the overall features of all the profiles remain the same.
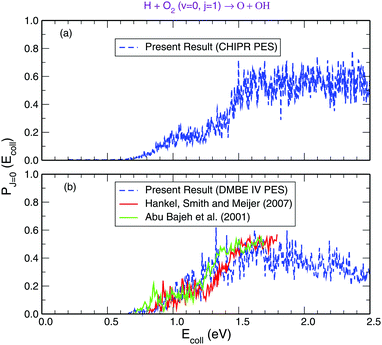 |
| | Fig. 1 Total reaction probability for the reaction H + O2 (v = 0, j = 1) → O + OH (v′,j′) compared with previous theoretical investigations.86,89 Panel-(a): on the CHIPR PES. Panel-(b): on the DMBE IV PES. | |
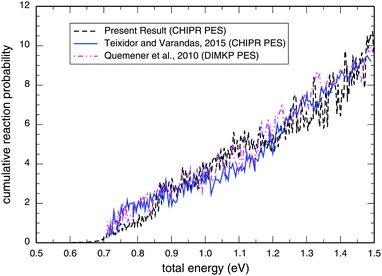 |
| | Fig. 2 Cumulative reaction probability (NJ=0(E)) as a function of the total energy for the reaction H + O2 → O + OH in comparison with previous theoretical investigations on the CHIPR93 and DIMKP68 PESs. | |
Fig. 3 shows the initial rovibrational state selected total reaction probabilities calculated on the CHIPR PES as a function of collision energy. It is quite evident from the profiles of the reaction probability for various initial rotational states of the O2 molecule that the vibrational excitation enhances the reaction probability to a large extent, whereas rotational excitation does not have that much influence on the total reaction probability. With the increase of initial vibrational state from v = 0 to v = 1, 2 and 3, the profiles for total reaction probability are seen to shift towards the left, which indicates a decrease in the threshold collision energy due to smaller effective barriers for higher vibrational states. Notably, for the initial state v = 3, such a reaction threshold diminishes to ∼0.1 eV. On the other hand, with the increase in initial rotational excitation from j = 1 to j = 3 and 5, the profiles shift slightly towards lower collision energies which causes only small alterations on the overall magnitude of the reaction probability. As it is visible, the trend of the profiles so obtained is more-or-less consistent with the calculations of Quéméner et al.68
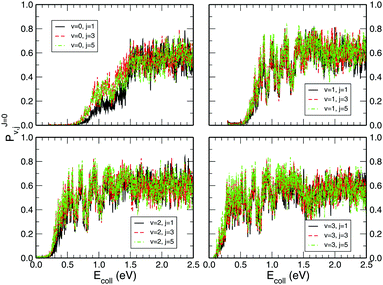 |
| | Fig. 3 Initial rotational state resolved total reaction probability for the H + O2 (v = 0, 1, 2, 3; j = 1, 3, 5) reaction as a function of collision energy. | |
Once the reaction probability is calculated for zero total angular momentum, J = 0, it is easy to calculate the integral cross section by invoking the J-shifting scheme. The integral cross sections for the initial v = 0, j = 1 rovibrational state of the O2 molecule in CHIPR and DMBE IV PES over the collision energy range 0.0–2.5 eV are displayed in Fig. 4. Other theoretical calculations by Varandas70 on the DMBE IV PES,39 and Quéméner et al. on the DIMKP PES as well as XXZLG PES68 are also shown together along with the available experimental findings by Keβler et al.,88 Abu Bajeh et al.89 and Seeger et al.90 The current profiles of integral cross section (both CHIPR and DMBE IV) show a threshold value of collision energy of ∼0.6 eV. Our calculated profile on the CHIPR PES shows a broad maximum at around ∼1.7 eV, which is in accordance with the general trend of experimental measurements by Keβler et al.88 and Seeger et al.,90 whereas the maximum seems to appear around ∼1.6 eV for the DMBE IV case. Notably, the present profile calculated on the CHIPR PES generally attains higher magnitude compared to the previous calculation by Quéméner et al., who performed TD quantum mechanical scattering calculations at J = 0 based on hyperspherical coordinates and invoked the J-shifting approximation to evaluate the integral cross-section. On the other hand, the calculated integral cross section on the DMBE IV PES is in quite good agreement with the previous QCT calculation by Varandas.70 In summary, the present result on the CHIPR PES shows good agreement with the experimental measurements of Keβler et al. and Seeger et al. especially in the lower collision energy range, whereas the profile for DMBE IV matches well with the same experimental profiles88,90 in the higher energy regime. Interestingly, our profiles also agree in shape with the curve reported by Varandas,70 who proposed to use quasiclassical trajectories to “extrapolate” accurate quantum mechanical results for J = 0, thence an alternative to the J-shifting scheme. Some quantitative differences between his results and the ones reported here may naturally be attributed to both the methodology and distinct potential energy surfaces that have been utilized.
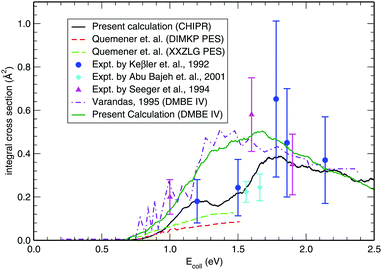 |
| | Fig. 4 Integral cross section for the H + O2 (v = 0, j = 1) reaction as a function of collision energy in comparison with previous theoretical results and experimental measurements. | |
While preforming the dynamics on the CHIPR PES for higher rovibrational states, viz. v = 1, 2, 3 and j = 1, 3, 5 of the O2 molecule, the state-specific integral cross sections shown in Fig. 5 seem to be largely influenced by the vibrational excitation from v = 0 to v = 1, 2 and 3, whereas the rotational excitation has little contribution to the magnitude of the cross section. Generally, the pattern of all the profiles is retained for all those rovibrational states, but the threshold collision energy gradually decreases with the higher vibrational state. Thus, we can say that with the increase in vibrational excitation, the title reaction tends gradually to be barrierless in nature. On the other hand, it is clearly visible that the initial rotational excitation of O2 does not alter the magnitude of the integral cross section, except for v = 0 where the profiles for j = 3 and 5 show a larger magnitude compared to the j = 1 case in the lower collision energy regime (0.0–1.5 eV). In addition, the threshold value decreases minutely with the increase in initial rotational state for all those initial vibrational states. Once again, the trends of our calculated profiles are in accordance with the previous calculations of Quéméner et al.68 Expectedly, by applying J-shifting approximation, the narrower and sharper resonance structures in the reaction probability at J = 0 get transmuted to ICS profiles. Those reaction probabilities for various initial rovibrational states at J = 0 show pronounced resonance structures (see Fig. 3) originating from the long-lived resonance states of HO2 due to its deep potential well.
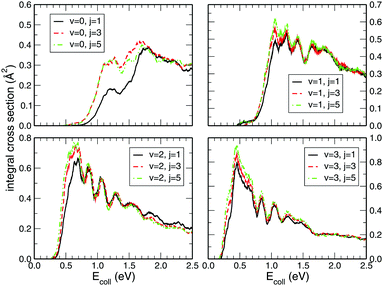 |
| | Fig. 5 Initial rovibrational state resolved integral cross section for the H + O2 (v = 0, 1, 2, 3; j = 1, 3, 5) reaction as a function of the collision energy. | |
While exploring the reliability of Bowman's J-shifting scheme,67 we have used Varandas's70 extrapolation scheme to calculate integral cross sections. Fig. 6 and 7 depict the results obtained from both methods: (a) J-shifting67versus (b) extrapolation of quantum mechanical J = 0 reaction probabilities with the help of QCT calculations for specific J values.70Fig. 6 shows that our reported integral cross sections on the CHIPR PES by J-shifting are in excellent agreement with the integral cross sections obtained via the extrapolation method. On the other hand, Fig. 7 also depicts that the cross sections calculated by these two approaches for the DMBE IV PES are in close agreement with each other, except for the fact that the J-shifted cross sections slightly overestimate the extrapolated results for Ecoll beyond 1.5 eV. Of course, one is led to think that the extrapolation scheme is probably more reliable for high collision energies, where the correspondence principle suggests that quantum results should approach their classical counterparts. It is perhaps not surprising that unlike the J-shifting case, the extrapolated cross section curve exhibits a profound oscillatory pattern, which basically originates from the rich resonance structure of the PJ=0 (v = 0,j = 1) profile. Thence, it should be viewed on an averaged sense. Since extrapolation of quantum results via classical mechanics is a quite natural thing to do for molecules of any size and it agrees quite well with the J-shifting results, the present theoretical prediction of experimental cross sections using both such methods appears to corroborate our better outcome when compared with other theoretical calculations.
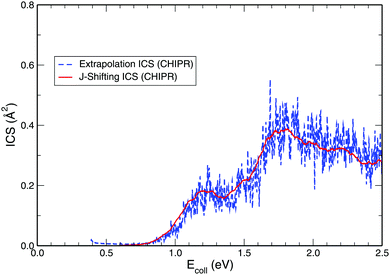 |
| | Fig. 6 Total integral cross section for the H + O2 (v = 0, j = 1) reaction as a function of the collision energy computed on the CHIPR PES by utilizing (a) J-shifting approximation and (b) the extrapolation method. | |
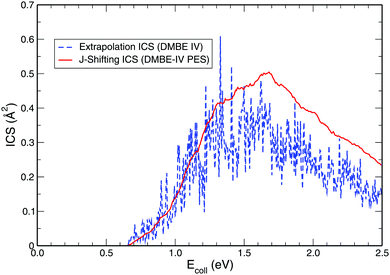 |
| | Fig. 7 Same as Fig. 6, but on the DMBE IV PES. | |
Employing the J = 0 reaction probability profile and using the J-shifting scheme, one may estimate the temperature-dependent rate coefficient. Fig. 8 depicts the Arrhenius plot of the Boltzmann averaged rate coefficient over the initial rovibrational states (v = 0–4; j = 1, 3, 5) as a function of inverse temperature for the temperature range 200–2000 K. Also included for comparison in Fig. 8 are previous results calculated by Teixidor and Varandas93 on the CHIPR PES and experimental measurements of Baulch et al.,58 Cohen and Westberg et al.57 and Warnatz.59 As shown, our results agree well with the experimental findings of Baulch et al.,58 particularly at the high temperature regime. Regarding the calculated profile of Teixidor and Varandas,93 no notable differences are observed except for the fact that ours lies slightly lower in magnitude compared to theirs over an intermediate temperature range of ∼500–1000 K.
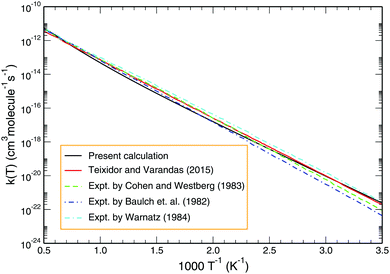 |
| | Fig. 8 Boltzmann averaged rate constant over the initial rovibrational states (v = 0–4; j = 1, 3, 5) for the reaction H + O2 as a function of temperature (black line) in comparison with the previous theoretical result and experimental findings. | |
To illustrate the effect of rovibrational excitation on the reactivity, Fig. 9 displays the thermal rate coefficients for various initial rovibrational states of O2 (v = 0–4; j = 1, 3, 5). From the Arrhenius plot of such state-specific thermal rate coefficients, one observes that rotational excitation does not show a large influence on the rate constant. Conversely, as we go to higher vibrational states, the profile of the rate coefficient changes drastically in the low temperature regime, whereas the effect is less pronounced at higher temperatures. In turn, the less negative slope of the rate coefficient profile for higher initial vibrational states indicates that the title reaction is evolving towards being barrierless in nature. In this case too, the trends of our calculated profiles are more-or-less consistent with the previous TI calculations by Teixidor and Varandas93 and Quéméner et al.68 Moreover, it is quite evident that as we increase the vibrational state of the O2 molecule from 0 to 4 at a particular rotational state, the difference among the profiles diminishes with increasing vibrational excitation. Additionally, the difference between the profiles seems to decrease further for higher rotational states. Since the rate coefficient does not change much for vibrational states above v = 4, the contribution from those rovibrational states on reactivity may be considered as an accurate estimation of the thermal rate coefficient.
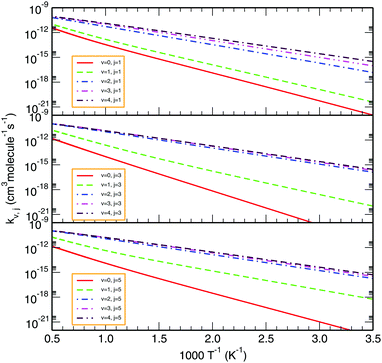 |
| | Fig. 9 Comparison of total rate constants for various initial rovibrational states of O2, viz., v = 0–4; j = 1, 3, 5. | |
The integral cross section and rate coefficient profiles for various initial rovibrational states have shown that the J-shifting approximation67 and the extrapolation technique70 are cost-effective approaches to obtain reliable estimation of such attributes. Quantum mechanical calculations using the fully close-coupling approach23 are computationally very demanding for all higher values of total angular momentum that are required to obtain converged results. Although the thermal rate coefficient reported here shows a slight deviation from the available experimental and theoretical results in the low temperature regime, the overall agreement is quite encouraging. On the other hand, the cross-section profile is also in good agreement with the experimental findings. We believe that the deviations can be overcome by performing fully close-coupled calculations for larger J values, an endeavor that we plan to tackle in future work by performing converged calculations for J > 0 cases with our parallelized quantum scattering code.
4 Summary
The TD 3D wave-packet calculations for the reaction H + O2 → O + OH have been performed on the recently reported CHIPR PES and also on the widely used DMBE IV PES. In particular, a detailed study on the effects of initial rovibrational excitation of the O2 molecule on the reactivity of this endoergic reaction has been presented. Various calculated reaction attributes have been found to be in good correspondence when compared with the previously reported accurate TI68,69,93 calculations. By using the popular J-shifting approximation (here supported by the results obtained by extrapolation70), an estimate of integral cross section profiles has also been made, with good agreement being observed between the results obtained from both the CHIPR and DMBE IV PESs, and the experimental data. Although some significant differences have been observed with some reported integral cross section profiles68 for the H + O2(v = 0, j = 1) reaction as a function of collision energy, a comparison with other calculated ones70,71 and experimental measurements88,90 has shown remarkable agreement. Moreover, a comparison of integral cross section profiles obtained by J-shifting with the ones calculated by extrapolation70 implies that the former may offer reliable scattering cross sections for the title reaction, particularly at low collision energies. A similar conclusion may also be drawn from the estimated thermal rate coefficient over the temperature range 200–2000 K. Of course, there is much scope for improvement, which can only be achieved by performing higher-J calculations with the fully close-coupled approach, a highly demanding computational endeavor that we plan for future work.
Conflicts of interest
There are no conflicts to declare.
Acknowledgements
SG acknowledges CSIR, India for the research fellowship. SA acknowledges DST-SERB, India through project no. File No. EMR/2015/001314 for research funding and thanks IACS for access to the CRAY super-computing facility. AJCV thanks the Fundação para a Ciência e a Tecnologia, Portugal, for support from the Coimbra Chemistry Centre through project PEst-OE/QUI/UI0313/2014. He also acknowledges the support from COST Action CM1405.
References
- A. Kuppermann, G. C. Schatz and M. Baer, J. Chem. Phys., 1976, 65, 4596–4623 CrossRef CAS.
- F. Webster and J. C. Light, J. Chem. Phys., 1989, 90, 265–299 CrossRef CAS.
- G. C. Schatz, Chem. Phys. Lett., 1988, 150, 92–98 CrossRef CAS.
- J. Z. H. Zhang and W. H. Miller, J. Chem. Phys., 1989, 91, 1528–1547 CrossRef CAS.
- M. Mladenovic, M. Zhao, D. G. Truhlar, D. W. Schwenke, Y. Sun and D. J. Kouri, J. Phys. Chem., 1988, 92, 7035–7038 CrossRef CAS.
- Y. T. Lee, Science, 1987, 236, 793 CAS.
- D. A. V. Kliner, D. E. Adelman and R. N. Zare, J. Chem. Phys., 1991, 95, 1648 CrossRef CAS.
- P. Casvecchia, Rep. Prog. Phys., 2000, 63, 355–414 CrossRef.
- X. Liu, J. J. Lin, S. A. Harich, G. C. Schatz and X. Yang, Science, 2000, 289, 1536–1538 CrossRef CAS PubMed.
- B. K. Kendrick, J. Chem. Phys., 2000, 112, 5679–5704 CrossRef CAS.
- D. Sokolovski and J. F. Castillo, Phys. Chem. Chem. Phys., 2000, 2, 507–512 RSC.
- A. J. H. M. Meijer and E. M. Goldfield, J. Chem. Phys., 1999, 110, 870–880 CrossRef CAS.
- D. H. Zhang, S. Y. Lee and M. Baer, J. Chem. Phys., 2000, 112, 9802–9809 CrossRef CAS.
- W. Zhu, T. Peng and J. Z. H. Zhang, J. Chem. Phys., 1997, 106, 1742–1748 CrossRef CAS.
- S. C. Althorpe, D. J. Kouri and D. K. Hoffmann, J. Chem. Phys., 1997, 106, 7629–7636 CrossRef CAS.
- J. C. Juanes-Marcos and S. C. Althorpe, Chem. Phys. Lett., 2003, 381, 743–750 CrossRef CAS.
- H. Gao, M. Sneha, F. Bouakline, S. C. Althorpe and R. N. Zare, J. Phys. Chem. A, 2015, 119, 12036–12042 CrossRef CAS PubMed.
- S. K. Gray and G. G. Balint-Kurti, J. Chem. Phys., 1998, 108, 950–962 CrossRef CAS.
- S. Y. Lin and H. Guo, Phys. Rev. A: At., Mol., Opt. Phys., 2006, 74, 022703/1–8 CAS.
- S. G. Carrasco and O. Roncero, J. Chem. Phys., 2006, 125, 054102/1–14 Search PubMed.
- Z. Sun, H. Guo and D. H. Zhang, J. Chem. Phys., 2010, 132, 084112/1–11 CAS.
- S. Adhikari and A. J. C. Varandas, Comput. Phys. Commun., 2013, 184, 270–283 CrossRef CAS.
- T. Sahoo, S. Ghosh, S. Adhikari, R. Sharma and A. J. C. Varandas, J. Phys. Chem. A, 2014, 118, 4837–4850 CrossRef CAS PubMed.
- T. Sahoo, S. Ghosh, S. Adhikari, R. Sharma and A. J. C. Varandas, J. Chem. Phys., 2015, 142, 024304/1–9 CrossRef CAS PubMed.
- G. D. Billing and N. Markovic, J. Chem. Phys., 1994, 100, 1085–1093 CrossRef.
- J. D. Kress, R. T. Pack and G. A. Parker, Chem. Phys. Lett., 1990, 170, 306–310 CrossRef CAS.
- S. Ghosh, T. Sahoo, S. Adhikari, R. Sharma and A. J. C. Varandas, J. Phys. Chem. A, 2015, 119, 12392–12403 CrossRef CAS PubMed.
- L. P. Viegas, A. Alijah and A. J. C. Varandas, J. Chem. Phys., 2007, 126, 074309/1–9 CrossRef CAS PubMed.
- F. C. Fehsenfeld, D. B. Dunkin, E. E. Ferguson and D. L. Albritton, Astrophys. J., 1973, 183, L25–L26 CrossRef CAS.
- D. Gerlich, Adv. Chem. Phys., 1992, 82, 1–176 CrossRef CAS.
- C. Schlier, U. Nowotny and E. Teloy, Chem. Phys., 1987, 111, 401–408 CrossRef CAS.
- T. S. Chu and K. L. Han, J. Phys. Chem. A, 2005, 109, 2050–2056 CrossRef CAS PubMed.
- P. Honvault and Y. Scribano, J. Phys. Chem. A, 2013, 117, 9778–9784 CrossRef CAS PubMed.
- S. Ghosh, S. Mukherjee, B. Mukherjee, S. Mandal, R. Sharma, P. Chaudhury and S. Adhikari, J. Chem. Phys., 2017, 147, 074105/1–16 CAS.
- S. Mukherjee, D. Mukhopadhyay and S. Adhikari, J. Chem. Phys., 2014, 141, 204306/1–13 CrossRef CAS PubMed.
- B. Sarkar and S. Adhikari, J. Chem. Phys., 2006, 124, 074101/1–18 CrossRef CAS PubMed.
- S. Ghosh, R. Sharma, S. Adhikari and A. J. C. Varandas, Chem. Phys. Lett., 2017, 675, 85–91 CrossRef CAS.
- A. J. C. Varandas, J. Chem. Phys., 2013, 138, 134117/1–7 CAS.
- M. R. Pastrana, L. A. M. Quintales, J. Brandao and A. J. C. Varandas, J. Phys. Chem., 1990, 94, 8073–8080 CrossRef CAS.
- D. Neuhauser, M. Baer, R. S. Judson and D. J. Kouri, Chem. Phys. Lett., 1990, 169, 372–379 CrossRef CAS.
- Y. Zhang, T.-X. Xie, K. L. Han and J. Z. H. Zhang, J. Chem. Phys., 2003, 119, 12921–12925 CrossRef CAS.
- T. S. Chu, T. X. Xie and K. L. Han, J. Chem. Phys., 2004, 121, 9352–9360 CrossRef CAS PubMed.
- R. F. Lu, T. S. Chu, Y. Zhang, K. L. Han, A. J. C. Varandas and J. Z. H. Zhang, J. Chem. Phys., 2006, 125, 133108/1–6 CAS.
- T. S. Chu, X. Zhang and K. L. Han, J. Chem. Phys., 2005, 122, 214301/1–6 CAS.
- T. S. Chu, A. J. C. Varandas and K. L. Han, Chem. Phys. Lett., 2009, 471, 222–228 CrossRef CAS.
- N. Markovic and G. D. Billing, Chem. Phys., 1995, 191, 247–260 CrossRef CAS.
- N. Markovic and G. D. Billing, Mol. Phys., 2000, 78, 1771–1781 CrossRef.
- D. H. Zhang and J. C. Light, J. Chem. Phys., 1996, 104, 4544–4553 CrossRef CAS.
- D. H. Zhang, M. Yang and S. Y. Lee, J. Chem. Phys., 2002, 117, 10067–10072 CrossRef CAS.
- D. H. Zhang and J. Z. H. Zhang, J. Chem. Phys., 1994, 101, 1146–1156 CrossRef CAS.
- N. Balakrishnan and G. D. Billing, J. Chem. Phys., 1994, 101, 2785–2792 CrossRef CAS.
- J. Qi, D. Lu, H. Song, J. Li and M. Yang, J. Chem. Phys., 2017, 146, 124303/1–8 CrossRef CAS PubMed.
- P. Sun, J. Chen, S. Liu and D. H. Zhang, Chem. Phys. Lett., 2017, 683, 352–356 CrossRef CAS.
- P. Y. Zhang, R. F. Lu, T. S. Chu and K. L. Han, J. Chem. Phys., 2010, 133, 174316/1–7 CAS.
-
W. C. Gardiner, Combustion Chemistry, Springer, Berlin, 1984 Search PubMed.
- H. Guo, Int. Rev. Phys. Chem., 2012, 31, 1–68 CrossRef CAS.
- N. Cohen and K. R. Westberg, J. Phys. Chem. Ref. Data, 1983, 12, 531–590 CrossRef CAS.
- D. L. Baulch, C. J. Cobos, R. A. Cox, P. Frank, G. Hayman, T. Just, J. A. Kerr, T. Murrells, M. J. Pilling, J. Troe, R. W. Walker and J. Warnatz, J. Phys. Chem. Ref. Data, 1994, 23, 847–1033 CrossRef CAS.
-
J. Warnatz, in Combustion Chemistry, ed. W. C. Gardiner, Springer-Verlag, New York, 1984 Search PubMed.
- K. S. Shin and J. V. Michael, J. Chem. Phys., 1991, 95, 262–273 CrossRef CAS.
- C. F. Melius and R. J. Blint, Chem. Phys. Lett., 1979, 64, 183–189 CrossRef CAS.
- B. Kendrick and R. T. Pack, J. Chem. Phys., 1995, 102, 1994–2012 CrossRef CAS.
- J. Troe and V. G. Ushakov, J. Chem. Phys., 2001, 115, 3621–3628 CrossRef CAS.
- C. Xu, D. Xie, D. H. Zhang, S. Y. Lin and H. Guo, J. Chem. Phys., 2005, 122, 244305 CrossRef PubMed.
- D. Xie, C. Xu, T. S. Ho, H. Rabitz, G. Lendvay, S. Y. Lin and H. Guo, J. Chem. Phys., 2007, 126, 074315 CrossRef PubMed.
- A. J. C. Varandas, J. Chem. Phys., 2013, 138, 054120 CrossRef CAS PubMed.
- J. Bowman, J. Phys. Chem., 1991, 95, 4960–4968 CrossRef CAS.
- G. Quéméner, B. K. Kendrick and N. Balakrishnan, J. Chem. Phys., 2010, 132, 014302 CrossRef PubMed.
- M. M. Teixidor and A. J. C. Varandas, Chem. Phys. Lett., 2015, 638, 61–65 CrossRef CAS.
- A. J. C. Varandas, Mol. Phys., 1995, 85, 1159–1164 CrossRef CAS.
- A. J. C. Varandas, Chem. Phys. Lett., 1995, 235, 111–118 CrossRef CAS.
- R. T. Pack, E. A. Butcher and G. A. Parker, J. Chem. Phys., 1993, 99, 9310–9313 CrossRef CAS.
- R. T. Pack, E. A. Butcher and G. A. Parker, J. Chem. Phys., 1995, 102, 5998–6012 CrossRef CAS.
- R. J. Duchovic and M. A. Parker, J. Phys. Chem. A, 2005, 109, 5883–5896 CrossRef CAS PubMed.
- S. Y. Lin, H. Guo, P. Honvault and D. Xie, J. Phys. Chem. B, 2006, 110, 23641–23643 CrossRef CAS PubMed.
- P. Bargueno, T. Gonzalez-Lezana, P. Larregaray, L. Bonnet and J. C. Rayez, Phys. Chem. Chem. Phys., 2007, 9, 1127–1137 RSC.
- S. Y. Lin, Z. Sun, H. Guo, D. H. Zhang, P. Honvault, D. Xie and S. Y. Lee, J. Phys. Chem. A, 2008, 112, 602–611 CrossRef CAS PubMed.
- Z. Sun, D. H. Zhang, C. Xu, S. Zhou, D. Xie, G. Lendvay, S. Y. Lee, S. Y. Lin and H. Guo, J. Am. Chem. Soc., 2008, 130, 14962–14963 CrossRef CAS PubMed.
- S. Y. Lin, H. Guo, G. Lendvay and D. Xie, Phys. Chem. Chem. Phys., 2009, 11, 4715–4721 RSC.
- A. Viel, C. Leforestier and W. H. Miller, J. Chem. Phys., 1998, 108, 3489–3497 CrossRef CAS.
- A. J. H. M. Meijer and E. M. Goldfield, J. Chem. Phys., 1998, 108, 5404–5413 CrossRef CAS.
- A. J. H. M. Meijer and E. M. Goldfield, J. Chem. Phys., 1999, 110, 870–880 CrossRef CAS.
- E. M. Goldfield and A. J. H. M. Meijer, J. Chem. Phys., 2000, 113, 11055–11062 CrossRef CAS.
- R. A. Sultanov and N. Balakrishnan, J. Phys. Chem. A, 2004, 108, 8759–8764 CrossRef CAS.
- S. Y. Lin, E. J. Rackham and H. Guo, J. Phys. Chem. A, 2006, 110, 1534–1540 CrossRef CAS PubMed.
- M. Hankel, S. C. Smith and A. J. H. M. Meijer, J. Chem. Phys., 2007, 127, 064316/1–9 CrossRef CAS PubMed.
- P. Honvault, S. Y. Lin, d. Xie and H. Guo, J. Phys. Chem. A, 2007, 111, 5349–5352 CrossRef CAS PubMed.
- K. Keβler and K. Kleinermanns, J. Chem. Phys., 1992, 97, 374–377 CrossRef.
- M. A. Bajeh, E. M. Goldfield, A. Hanf, C. Kappel, A. J. H. M. Meijer, H. R. Volpp and J. Wolfrum, J. Phys. Chem. A, 2001, 105, 3359–3364 CrossRef CAS.
- S. Seeger, V. Sick, H. R. Volpp and J. Wolfrum, Isr. J. Chem., 1994, 34, 5–18 CrossRef CAS.
- B. R. Johnson, J. Chem. Phys., 1983, 79, 1916–1925 CrossRef CAS.
- G. D. Billing and N. Markovic, J. Chem. Phys., 1993, 99, 2674–2681 CrossRef CAS.
- M. M. Teixidor and A. J. C. Varandas, J. Chem. Phys., 2015, 142, 014309/1–10 CrossRef CAS PubMed.
- D. Neuhasuer and M. Baer, J. Chem. Phys., 1989, 90, 4351–4355 CrossRef CAS.
- D. Kosloff and R. Kosloff, J. Comput. Phys., 1986, 52, 35–53 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c7cp06254k |
|
| This journal is © the Owner Societies 2018 |
Click here to see how this site uses Cookies. View our privacy policy here.  *a and
António J. C.
Varandas
*c
*a and
António J. C.
Varandas
*c
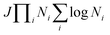 , where J is the total angular momentum and Ni is the number of basis functions for the ith internal coordinate. Billing and Markovic25 formulated such a four-dimensional (4D) quantum mechanical problem of triatomic reactive scattering using hyperspherical coordinates and performed calculations for the D + H2 system in the simplest cases of J = 0, and J = 1. This approach was further transmuted by Adhikari and Varandas22 for the extension to higher J ≠ 0 situations. The state-to-state as well as total cross sections and rate coefficients have been accurately calculated by Adhikari and coworkers via the implementation of an OpenMP-MPI parallelized algorithm for the TD wave packet approach to the D+ + H2 system using both the lowest adiabatic singlet sheet (11A′)23,24 and lowest three singlet sheets (11A′, 21A′ and 31A′)27 of the double many-body expansion (DMBE) PES for H3+ reported by Varandas and coworkers.28 The results were found to be in good agreement with experimental observations29–31 and previous theoretical calculations.32,33 Very recently, Adhikari and coworkers34 constructed accurate diabatic potential energy surfaces for the lowest three singlet states of H3+
, where J is the total angular momentum and Ni is the number of basis functions for the ith internal coordinate. Billing and Markovic25 formulated such a four-dimensional (4D) quantum mechanical problem of triatomic reactive scattering using hyperspherical coordinates and performed calculations for the D + H2 system in the simplest cases of J = 0, and J = 1. This approach was further transmuted by Adhikari and Varandas22 for the extension to higher J ≠ 0 situations. The state-to-state as well as total cross sections and rate coefficients have been accurately calculated by Adhikari and coworkers via the implementation of an OpenMP-MPI parallelized algorithm for the TD wave packet approach to the D+ + H2 system using both the lowest adiabatic singlet sheet (11A′)23,24 and lowest three singlet sheets (11A′, 21A′ and 31A′)27 of the double many-body expansion (DMBE) PES for H3+ reported by Varandas and coworkers.28 The results were found to be in good agreement with experimental observations29–31 and previous theoretical calculations.32,33 Very recently, Adhikari and coworkers34 constructed accurate diabatic potential energy surfaces for the lowest three singlet states of H3+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 35 using first principle-based beyond Born–Oppenheimer theory36 and performed quantum dynamics using this hyperspherical coordinate-based scattering code on those surfaces to calculate state-to-state integral cross sections and found an overwhelming agreement with most recent available experimental data for all three competing charge transfer channels. In a similar context, Adhikari, Varandas and coworkers employed the same methodology for the O + OH reaction37 using both the (combined-hyperbolic-inverse-power-representation) CHIPR38 and DMBE IV PESs39 of HO2 and the J-shifting approximation to calculate state-to-state thermal rate coefficients. Moreover, 3D as well as coupled 3D time-dependent wave packet approaches have been employed for several other triatomic reactions in Jacobi coordinates, viz., F + H2,40,41 O(1D) + N2,42 H + D2,43 O + H2,44 D + H2 and H + D245etc. and in hyperspherical coordinates, viz., D + H2,22,25 D+ + H2,23,24,27,34,46 F + H2,47etc. On the other hand, going beyond the atom–diatom to polyatomic reactive scattering is a big challenge in quantum dynamics, since the major bottleneck is to handle the exponential increase in computational cost due to the increase in mathematical dimensionalities when the number of atoms involved in the collision increases from three to four. For example, the dimensionality in terms of internal degrees of freedom increases from three for a triatomic system to six for a tetra-atomic system. On the contrary, the main computational advantage of a time-dependent approach is its smaller computational scaling with the number of basis functions (≤N2vs. N3 in the standard CC time-independent method). Owing to its favorable computational scaling, the time-dependent approach is preferred for some large-scale computational tasks for various large molecules in reaction dynamics. In addition to that, utilization of hyperspherical coordinates is advantageous as it is able to handle all the reactant and product channels evenhandedly. To summarize, the rigorous dynamical treatment for tetra-atomic reactions is still not performed in hyperspherical coordinates, although a few calculations have been reported by using the time-dependent wave packet methodology in Jacobi coordinates for various tetra-atomic reactions, viz. H + H2O,48–51 H + H2S,52 H + CO2,53 OH + D254etc.
35 using first principle-based beyond Born–Oppenheimer theory36 and performed quantum dynamics using this hyperspherical coordinate-based scattering code on those surfaces to calculate state-to-state integral cross sections and found an overwhelming agreement with most recent available experimental data for all three competing charge transfer channels. In a similar context, Adhikari, Varandas and coworkers employed the same methodology for the O + OH reaction37 using both the (combined-hyperbolic-inverse-power-representation) CHIPR38 and DMBE IV PESs39 of HO2 and the J-shifting approximation to calculate state-to-state thermal rate coefficients. Moreover, 3D as well as coupled 3D time-dependent wave packet approaches have been employed for several other triatomic reactions in Jacobi coordinates, viz., F + H2,40,41 O(1D) + N2,42 H + D2,43 O + H2,44 D + H2 and H + D245etc. and in hyperspherical coordinates, viz., D + H2,22,25 D+ + H2,23,24,27,34,46 F + H2,47etc. On the other hand, going beyond the atom–diatom to polyatomic reactive scattering is a big challenge in quantum dynamics, since the major bottleneck is to handle the exponential increase in computational cost due to the increase in mathematical dimensionalities when the number of atoms involved in the collision increases from three to four. For example, the dimensionality in terms of internal degrees of freedom increases from three for a triatomic system to six for a tetra-atomic system. On the contrary, the main computational advantage of a time-dependent approach is its smaller computational scaling with the number of basis functions (≤N2vs. N3 in the standard CC time-independent method). Owing to its favorable computational scaling, the time-dependent approach is preferred for some large-scale computational tasks for various large molecules in reaction dynamics. In addition to that, utilization of hyperspherical coordinates is advantageous as it is able to handle all the reactant and product channels evenhandedly. To summarize, the rigorous dynamical treatment for tetra-atomic reactions is still not performed in hyperspherical coordinates, although a few calculations have been reported by using the time-dependent wave packet methodology in Jacobi coordinates for various tetra-atomic reactions, viz. H + H2O,48–51 H + H2S,52 H + CO2,53 OH + D254etc.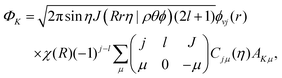
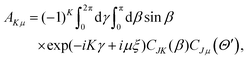
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Θ′ = −sin
Θ′ = −sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β
β![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos
cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) γ,
γ,![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ξ = cos
ξ = cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β/sin
β/sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Θ′,
Θ′,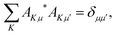
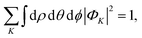
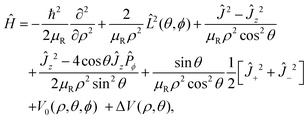
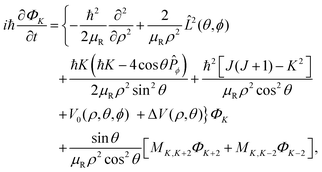
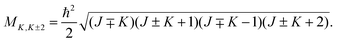
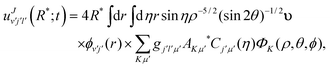
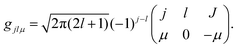
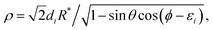
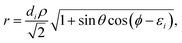
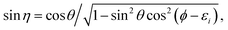
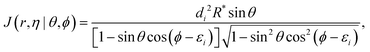
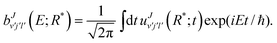
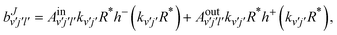
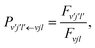
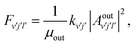
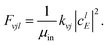
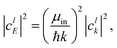
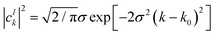
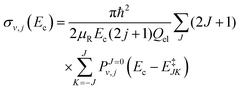
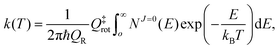
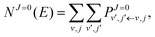
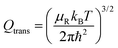
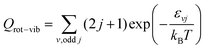
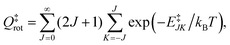
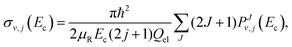
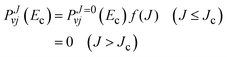
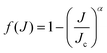
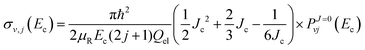
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/i_char_2009.gif) log
log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/i_char_2009.gif) N, with N being the total number of grid points on the ρ, θ and ϕ coordinates. Time propagation of the wave packet is monitored by the iterative Lanczos reduction technique, which is basically a short time propagator. The demand of huge computational cost is illustrated elsewhere22,23 with the detailed discussion about the implementation of the OpenMP-MPI parallelization scheme.23,27
N, with N being the total number of grid points on the ρ, θ and ϕ coordinates. Time propagation of the wave packet is monitored by the iterative Lanczos reduction technique, which is basically a short time propagator. The demand of huge computational cost is illustrated elsewhere22,23 with the detailed discussion about the implementation of the OpenMP-MPI parallelization scheme.23,27