Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Formation and structure of the ferryl [Fe![[double bond, length as m-dash]](https://www.rsc.org/images/entities/h2_char_e001.gif) O] intermediate in the non-haem iron halogenase SyrB2: classical and QM/MM modelling agree†
O] intermediate in the non-haem iron halogenase SyrB2: classical and QM/MM modelling agree†
G.
Rugg
and
H. M.
Senn
 *
*
WestCHEM and School of Chemistry, University of Glasgow, Glasgow G12 8QQ, Scotland, UK. E-mail: hans.senn@glasgow.ac.uk
First published on 31st October 2017
Abstract
To rationalise mechanistically the intriguing regio- and chemoselectivity patterns for different substrates of the non-haem iron/2-oxoglutarate dependent halogenase SyrB2, it is crucial to elucidate the structure of the pivotal [FeIV![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O] intermediate. We have approached the problem by a combination of classical and QM/MM modelling. We present complete atomistic models of SyrB2 in complex with its native substrate L-threonine as well as L-α-amino butyric acid and L-norvaline (all conjugated to the pantetheine tether), constructed by molecular docking and extensive MD simulations. We evaluate five isomers of the [Fe
O] intermediate. We have approached the problem by a combination of classical and QM/MM modelling. We present complete atomistic models of SyrB2 in complex with its native substrate L-threonine as well as L-α-amino butyric acid and L-norvaline (all conjugated to the pantetheine tether), constructed by molecular docking and extensive MD simulations. We evaluate five isomers of the [Fe![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O] intermediate in these simulations, with a view to identifying likely structures based on a simple “reaction distance” measure. Starting from models of the resting state, we then use QM/MM calculations to investigate the formation of the [Fe
O] intermediate in these simulations, with a view to identifying likely structures based on a simple “reaction distance” measure. Starting from models of the resting state, we then use QM/MM calculations to investigate the formation of the [Fe![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O] species for all three substrates, identifying the intermediates along the O2 activation/decarboxylation pathway on the S = 1, 2, and 3 potential-energy surfaces. We find that, despite differences in the detailed course of the reaction, essentially all pathways produce the same [Fe
O] species for all three substrates, identifying the intermediates along the O2 activation/decarboxylation pathway on the S = 1, 2, and 3 potential-energy surfaces. We find that, despite differences in the detailed course of the reaction, essentially all pathways produce the same [Fe![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O] structure, in which the oxido is directed away from the substrate.
O] structure, in which the oxido is directed away from the substrate.
Introduction
Non-haem iron (NHFe) halogenases have been the focus of much attention due to their unique ability to install halogens at unreactive positions in complex substrates with exquisite chemo- and regioselectivity. The interest in biological halogenation generally has been boosted over the last decade by the discovery of several new classes and families of halogenases; the progress has been extensively reviewed,1–12 most recently by Moore and co-workers.12 Beyond the fundamental biosynthetic and mechanistic interest, halogenases have attracted attention as “green” catalysts for biotechnological and biocatalytic applications.10,11,13,14The NHFe halogenase SyrB215 is the type specimen of the class of radical halogenases, which activate environmentally abundant halide anions (X−) as halogen radicals (X˙) for incorporation into organic substrates. SyrB2 was the first NHFe halogenase to be characterised structurally16 and is by far the most thoroughly studied. About a dozen NHFe halogenases have so far been characterised biochemically, but only four of them also structurally.12 SyrB2 stems from the plant-pathogenic bacterium Pseudomonas syringae, where it is part of the biosynthetic pathway for the production of syringomycin E, a cyclic lipopeptide with phytotoxic and antifungal activity. Like the majority of NHFe halogenases, SyrB2 chlorinates the aliphatic side-chain of an α-amino acid. Specifically, it installs chlorine at the terminal methyl group of L-threonine (Scheme 1), before the modified residue is integrated into the growing product. The enzyme requires oxygen and 2-oxoglutarate (2OG) as co-substrates, which are turned over into CO2 and succinate.
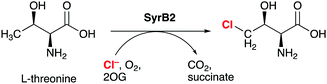 | ||
| Scheme 1 SyrB2 catalyses the chlorination of L-threonine at the terminal side-chain carbon. 2-OG = 2-oxoglutarate. | ||
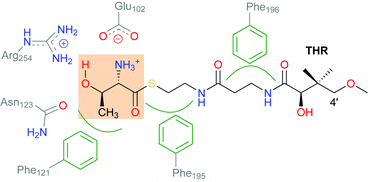
SyrB2 does not recognise free threonine as a substrate. The amino acid needs to be conjugated to a phosphopantetheine tether (see Scheme 2) and presented to the enzyme by a carrier protein. This requirement has so far prevented the experimental determination of the structure of the enzyme–substrate complex, and thus, the exact set-up and configuration of the active site with bound substrate remain elusive. The same applies to all NHFe halogenases reported to date, with one recent exception: WelO5 (and its close homologue AmbO5) chlorinate freestanding substrates, which enabled the first crystal structure of a NHFe halogenase in complex with its substrate to be obtained.17 While this result will undoubtedly further the elucidation of the mechanism of NHFe halogenases in general and WelO5 in particular, the structural details are not directly transferable. Although all NHFe halogenases share a common make-up of the active-site iron complex, WelO5 belongs to a different family that chlorinates cyclohexane rings in alkaloid scaffolds whereas SyrB2 (and most other NHFe halogenases) work on aliphatic side-chains of α-amino acids.
The mechanism of the NHFe halogenases (Scheme 3) is closely related to that of the NHFe hydroxylases, which is well studied.18 The main difference is the set of first-shell ligands: in the hydroxylases, the iron is coordinated by two His imidazoles and an Asp or Glu carboxylate, which form the 2-His-1-Asp/Glu “facial triad” motif. In the halogenases, the carboxylate is replaced by a halide. In the resting state A-H2O, the Fe(II) centre is octahedrally coordinated by two His, the chelating 2OG, chloride, and water. Substrate binding triggers water dissociation (A), opening up a free coordination site for O2 to bind (B). The O2-bound complex B undergoes O2 activation and decarboxylation (C1 and C2 denoting intermediates before and after decarboxylation, respectively), yielding the FeIV–oxido (ferryl) intermediate D. This intermediate is central for the reactivity, having the capability to abstract an unactivated hydrogen from the substrate. In the subsequent “rebound” step, the substrate radical combines with the chlorido ligand of E to form the chlorinated product.
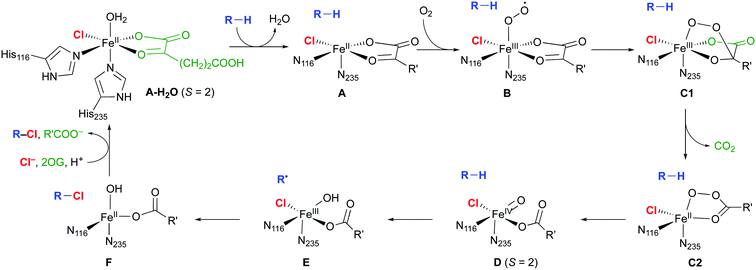 | ||
| Scheme 3 Proposed catalytic cycle in NHFe/2OG dependent halogenases; the residue numbering refers to SyrB2. R is an aliphatic carbon of the substrate; R′ = (CH2)2COO−. | ||
Except for A-H2O,16 the structures, and in some cases the existence, of the intermediates shown in Scheme 3 are not known experimentally. The [Fe![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O] species D at least is sufficiently long-lived to allow its spectroscopic characterisation in SyrB2 (or the close homologue CytC3), notably by Mössbauer techniques.19–22 Nuclear resonance vibrational spectroscopy (NRVS) combined with DFT modelling22 strongly suggested that D is five-coordinate, with oxido trans to His116 (as drawn in Scheme 3). Previously, it had been assumed that the oxido was formed trans to His235 and that succinate was bidentate.23–27
O] species D at least is sufficiently long-lived to allow its spectroscopic characterisation in SyrB2 (or the close homologue CytC3), notably by Mössbauer techniques.19–22 Nuclear resonance vibrational spectroscopy (NRVS) combined with DFT modelling22 strongly suggested that D is five-coordinate, with oxido trans to His116 (as drawn in Scheme 3). Previously, it had been assumed that the oxido was formed trans to His235 and that succinate was bidentate.23–27
The overall selectivity of the reaction is determined by two steps: the (slow) H-abstraction D → E controls the position at which the substrate radical is formed and thus the regioselectivity. The (fast) rebound E → F governs the chemoselectivity: the substrate radical can in principle combine with either the OH or the Cl ligand of intermediate E, leading to hydroxylation or chlorination, respectively. With its native substrate THR, SyrB2 has an almost complete selectivity for chlorination, but in reaction with related α-amino acid substrates, it is equally competent at hydroxylation (Scheme 4). ABA (L-α-amino butyric acid or (S)-2-aminobutanoic acid), which lacks THR's OγH group, yields a mixture of hydroxylated and chlorinated product, the substitutions taking place at the terminal methyl only. NVA (L-norvaline or (S)-2-aminopentanoic acid) has an extra methylene group and is converted into the 4-Cl, 4-OH, and 5-OH derivatives.
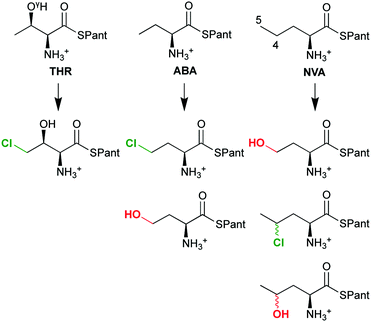 | ||
| Scheme 4 The chemo- and regioselectivity of SyrB2 is dependent on the substrate: THR (L-threonine), ABA (L-α-amino butyric acid), NVA (L-norvaline); Pant = pantetheine. | ||
The questions as to how the enzyme controls selectivity and what factors determine the outcome for a particular substrate have been actively investigated.20–22,27,28 From these studies emerged the concept that the positioning of the substrate relative to the oxido oxygen in D (and the Cl and OH ligands in E) is decisive. If the C–H bond is close to the oxido in D, the resulting Fe–OH and substrate radical will also be close, favouring hydroxylation. However, this reactivity is suppressed by positioning the C–H further away from the oxido and closer to the Cl, trading efficiency for selectivity. This is consistent with slow H-abstraction (and overall) rates for chlorination (4.2 min−1 for THR) compared to hydroxylation (480 min−1 for 5-hydroxylation of NVA).28
The precise structure of the [Fe![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O] intermediate D is thus pivotal for an understanding of the intriguing selectivity of SyrB2. The lack of an experimental structure with bound substrate, the conformational flexibility of the substrate, the variable coordination geometry of the iron centre, and the interactions of the active-site complex with the protein environment make this a challenging problem for computational modelling. A number of computational studies22–27,29–31 have addressed different aspects of the reactivity of SyrB2. Having established the structure of D from their NRVS/computational results,22 Solomon and co-workers recently investigated in detail the intrinsic electronic factors affecting the reactivity and selectivity of H-abstraction and Cl/OH transfer.30,31 All studies used QM (DFT) cluster models, with selected active-site residues surrounding the iron complex. The only exception are Shaik and co-workers,29 who employed a full QM/MM model. Starting from intermediate D, they delineated the role of specific interactions of the reaction intermediates with active-site residues in controlling the selectivity.
O] intermediate D is thus pivotal for an understanding of the intriguing selectivity of SyrB2. The lack of an experimental structure with bound substrate, the conformational flexibility of the substrate, the variable coordination geometry of the iron centre, and the interactions of the active-site complex with the protein environment make this a challenging problem for computational modelling. A number of computational studies22–27,29–31 have addressed different aspects of the reactivity of SyrB2. Having established the structure of D from their NRVS/computational results,22 Solomon and co-workers recently investigated in detail the intrinsic electronic factors affecting the reactivity and selectivity of H-abstraction and Cl/OH transfer.30,31 All studies used QM (DFT) cluster models, with selected active-site residues surrounding the iron complex. The only exception are Shaik and co-workers,29 who employed a full QM/MM model. Starting from intermediate D, they delineated the role of specific interactions of the reaction intermediates with active-site residues in controlling the selectivity.
In this contribution, we present complete atomistic models of SyrB2 in complex with THR, ABA, and NVA, constructed by molecular docking and extensive MD simulations. We evaluate isomers of the [Fe![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O] intermediate D in these simulations, with a view to identifying plausible structures based on classical simulations alone. We then use for the first time QM/MM calculations on full-enzyme models and follow the O2 activation/decarboxylation pathway B → D for all three substrates on the S = 1, 2, and 3 potential-energy surfaces. We find that, despite differences in the detailed course of the reaction, essentially all pathways produce the same isomer of D, labelled D1, in which the oxido is trans to His116.
O] intermediate D in these simulations, with a view to identifying plausible structures based on classical simulations alone. We then use for the first time QM/MM calculations on full-enzyme models and follow the O2 activation/decarboxylation pathway B → D for all three substrates on the S = 1, 2, and 3 potential-energy surfaces. We find that, despite differences in the detailed course of the reaction, essentially all pathways produce the same isomer of D, labelled D1, in which the oxido is trans to His116.
Computational details
Structure preparation
The entire modelling is based on the single-crystal X-ray structure of the SyrB2 holoprotein (PDB code 2FCT16), which contains the active-site [FeIICl(2OG)(H2O)]− complex (A-H2O). A few residues (Met1–Ser2 and Ile57–Ser58–Gly59–Gly60) are not resolved in that structure and were completed using the loop-modelling tools of Modeller.32,33 The program Reduce34,35 was used to check for, and rectify, flipped Asn/Gln/His residues, and protonation states of titratable residues were assigned with PropKa.36,37 Further details are available in the ESI.†Molecular docking
AutoDock Vina38,39 (referred to as Vina from here on) was used for docking as it is able to handle fairly large numbers of rotatable bonds reliably and efficiently.38,40 (Note that Vina uses a scoring function and global-search algorithm different from AutoDock's.) The substrates were built by conjugating the respective α-amino acid (with protonated amino group) as a thioester to pantetheine (modified by methylating the 4′-OH group; see Scheme 2). The substrate structures were optimised at DFT level (see the ESI†). In the docking procedure, the substrates were fully flexible; that is, all single bonds were rotatable, except for the amide and thioester bonds (which have partial double-bond character) and bonds whose rotation would generate symmetry-equivalent conformers (–CH3, –NH3+). Hence, THR and NVA had 15 rotatable bonds and ABA had 14. Three bonds in the protein were also designated as rotatable: Cα–Cβ and Cβ–Cγ of Phe196 and Cζ–OH of Tyr272. The docking box of 24 × 20 × 16 Å enclosed the active-site cavity and the channel connecting to the protein surface. Each docking run was set to produce 20 poses.Molecular dynamics simulations
MD simulations in explicit water solvent under periodic boundary conditions were run for the following systems: apoprotein; holoprotein; enzyme–substrate complexes A with THR, NVA, and ABA, commencing from the most favourable docked pose for each substrate; and 15 enzyme–substrate complexes D (five isomers of D for each substrate). To prepare the simulations of D, a representative snapshot was taken from the respective simulation of A and the active-site iron complex replaced by a DFT-optimised complex D. The succinate ligand and the substrate were optimised at MM level, keeping the rest of the system frozen, to resolve any steric clashes before starting the MD simulation protocol.The Gromacs suite of programs41–43 was used throughout, with the Amber ff03 forcefield44 for the protein, GAFF45,46 for the active-site complexes and substrates, and TIP3P water.47 RESP charges for non-standard residues (substrates, active-site complexes) were derived using the Merz–Singh–Kollman scheme.48 Topology and parameter files for use with Gromacs were generated using AmberTools49 and ACPYPE.50,51 The iron atom and the first shell of donor atoms were fixed by harmonic position restraints with a force constant of 104 kJ mol−1 nm−2. After preliminary energy minimisation and pressure equilibration, the simulations were run in the NVT ensemble until deemed equilibrated, followed by production runs of 17–27 ns; see the ESI† for additional details. The simulations included ca. 35![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 atoms, with the protein (including cofactors) accounting for ca. 4850, the substrate for ca. 60, and the solvent for the remainder.
000 atoms, with the protein (including cofactors) accounting for ca. 4850, the substrate for ca. 60, and the solvent for the remainder.
QM and QM/MM calculations
QM-only optimisations of complexes D in the quintet state were performed at B3LYP/def2-TZVP+/PCM (ε = 3.9) level; see the ESI† for details. All QM/MM calculations were carried out with ChemShell,52,53 which was interfaced to Turbomole54–57 as external QM engine. ChemShell's internal force-field engine was used for the MM contributions. The QM–MM boundary was treated with a hydrogen link-atom scheme with charge shifting. Electrostatic embedding was used, allowing for polarisation of the QM density by the MM point charges; no cut-off was applied to the QM–MM electrostatic interactions. Structure optimisations were performed with a microiterative scheme58 in hybrid delocalised coordinates (HDLC)59 as implemented in the DL-FIND module60 in ChemShell.QM calculations were done at the DFT level with the B3LYP61–66 exchange–correlation functional (as implemented in Turbomole), complemented by Grimme's D3 dispersion correction.67 Reaction-coordinate scans and optimisations were initially done with the def2-SVP basis set, stationary points were then re-optimised with def2-TZVP.68 Reported results were obtained at the def2-TZVP level unless stated otherwise. The MM parameters were the same as in the MD simulations described above.
The QM region comprised the active-site iron complex with all first-shell ligands (with histidines truncated to 5-methylimidazoles, 2OG truncated to 2-oxopropanoate or acetate + CO2, respectively), the substrate head (truncated at the C(O)–Cα bond), and the acetate side-chain of Glu102. The latter was included to allow for proton transfers across the substrate–NH3+–Glu102 salt bridge. For THR, where the direct salt bridge was replaced by a water-mediated interaction during the MD simulations, the two bridging water molecules were also included in the QM region. In the event, we did not observe any proton transfers in any of the calculations. The QM region included 65 atoms (including 5 link atoms); the MM region contained 6802 atoms: the entire enzyme (including substrate) and a sphere of 650 water molecules within 23 Å of the iron (numbers refer to THR). See the ESI† for further details of the QM/MM setup.
Mössbauer spectroscopic parameters were calculated with ORCA69,70 at the B3LYP61–66/def2-TZVP68 level with the efficient RIJCOSX method.71 The full set of point charges from the QM/MM models was included in the calculations. To ensure an accurate description of the density at the iron nucleus, the CP(PPP) basis72 was used for iron, together with a dense radial integration grid at iron (accuracy parameter 7.0). The Mössbauer isomer shift, δ, is related to the calculated density at the nucleus, ρ0, via the linear relationship δ = α(ρ0 − C) + β, where α = −0.366 a03 mm s−1, β = 2.852 mm s−1, and C = 11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 810 a0−3 are fit parameters specific to the choice of functional and basis set.73 Alternative fit parameters have been derived from a larger and more diverse training set:74α = −0.424 a03 mm s−1, β = 7.55 mm s−1, and C = 11
810 a0−3 are fit parameters specific to the choice of functional and basis set.73 Alternative fit parameters have been derived from a larger and more diverse training set:74α = −0.424 a03 mm s−1, β = 7.55 mm s−1, and C = 11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 800 a0−3.
800 a0−3.
Results and discussion
Modelling the enzyme–substrate complex
The docking procedure was based on the X-ray structure of the SyrB2 holoenzyme in the resting state; the Fe-bound water molecule was removed, creating intermediate A. The protein was kept rigid, except for the two side-chain torsions of Phe196 and the Cζ–OH torsion of Tyr272. Flexibility of Phe196, which is located near the entrance of the channel, was deemed to be relevant as its side-chain hinders access to the channel in the X-ray structure and has been suggested to act as a “gate-keeper”.16 The OH group of Tyr272, located at the end of the channel towards the active-site cavity, has been proposed as a possible hydrogen-bonding partner of the substrate head, so rotation about this torsion was also allowed.
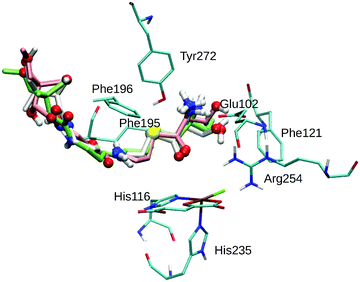
Table 1 lists the affinities and RMSDs from the top pose for the ten most favourable docked poses for THR as obtained from the Vina docking procedure. The structures of the three best poses are shown overlaid in Fig. 1. As is evident from the RMSDs, Poses 1–4 are structurally very similar whereas the remaining poses differ significantly. The small structural variability in Poses 1–4 stems mostly from the pantetheine tail end (see Fig. 1), which extended beyond the substrate channel into the solvent and is conformationally less constrained. Only in Poses 1–4 was the substrate's reacting methyl group placed sufficiently close to the iron complex to make a reaction appear feasible. In the other poses, the substrate head was positioned away from the reactive centre or the substrate as a whole was partially retracted from the channel.
| Pose no. | Affinity/(kJ mol−1) | RMSD/Å |
|---|---|---|
| 1 | −33.5 | 0.00 |
| 2 | −32.6 | 1.41 |
| 3 | −32.2 | 1.71 |
| 4 | −31.4 | 1.68 |
| 5 | −29.7 | 9.96 |
| 6 | −29.7 | 3.29 |
| 7 | −29.3 | 9.71 |
| 8 | −28.9 | 9.36 |
| 9 | −28.9 | 9.70 |
| 10 | −28.9 | 10.13 |
THR in Poses 1–4 is stabilised by hydrophobic interactions with Phe121 in the active-site cavity and Phe195 and Phe196 in the channel, in agreement with the participation of these residues in substrate stabilisation suggested based on mutation studies.75 The flexible Phe196 benzyl side chain re-oriented as expected so as to grant the substrate access to the active-site channel. Whereas previous studies26,27,29,75 adjusted the side-chain torsions manually to allow access to the channel, keeping Phe196 rigid during subsequent docking, we find that this conformational change is intrinsically favoured by the interactions with the incoming substrate.
Most relevant for the exact positioning of the reacting C–H bond are the potentially strong, directing interactions of the substrate head. The ammonium group is well set up to form a salt bridge with the side-chain carboxylate of Glu102. Indeed, THR formed a strong hydrogen bond/salt bridge between its ammonium group and Glu102 in Poses 1–3 (shown in Fig. 1) while Pose 4 lacks this interaction. This salt bridge was also present in previous docking studies,26,75 and the Glu102Ala mutant was found to be inactive,75 which supports the importance of this interaction.
While any α-amino acid substrate will feature the ammonium group in the same position and therefore be able to form such a salt bridge, THR in addition has the possibility to form a second directing interaction by hydrogen-bonding via its OγH group. We found OγH bonding either to Arg254 (Pose 1) or to Glu102 (Poses 2 and 3); no such hydrogen-bond exists in Pose 4. Previous studies found the OH group bonding to Glu10226 or Asn123.75 Tyr272, whose Cζ–OH bond was treated as rotatable to allow for hydrogen-bonding to the substrate OH or ammonium groups, did not form any such hydrogen bond in any of the poses (nor in the subsequent MD simulations).
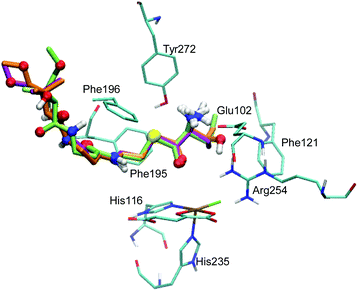
The docking of ABA and NVA yielded sets of poses very similar to THR (see Tables S3 and S4, ESI†). Like in the case of THR, the four and five best-scoring poses for ABA and NVA, respectively, place the substrate head sufficiently close to the iron centre to make a reaction plausible. Again, these top poses are structurally highly similar, with small differences in the tail end. Comparing the top poses for the three substrates (see Fig. 2 and Table 2), they are essentially identical, featuring very similar substrate ammonium–Glu102 salt bridges and hydrophobic stabilisation from Phe121, Phe195, and Phe196.
| Substrate | Method | Glu102 dSB/Å | Phe121 dRH/Å | Phe195 dRH/Å | Phe196 dRH/Å |
|---|---|---|---|---|---|
| THR | Docking | 1.92 | 3.64 | 3.46 | 3.36 |
| MD | 3.85 | 5.44 | 3.23 | 2.86 | |
| ABA | Docking | 2.10 | 3.73 | 3.52 | 3.10 |
| MD | 1.82 | 5.25 | 3.10 | 2.74 | |
| NVA | Docking | 2.17 | 3.75 | 3.49 | 2.16 |
| MD | 1.74 | 4.42 | 2.85 | 2.95 | |
The close agreement in terms of substrate conformations and positions – both within the set of best-scoring poses for any one substrate and between the top poses for the three different substrates – means that one can expect a molecular-dynamics trajectory of reasonable length, starting from any of the poses, to explore the full conformational space spanned by the set of relevant poses.
For ABA and NVA, the conformations and characteristic protein–substrate interactions as obtained from docking were largely maintained during the MD simulations; see Table 2. In particular, the salt bridge between the substrate ammonium group and the Glu102 carboxylate, which anchors the substrate head, was stable and preserved throughout.
THR, on the other hand, changed its conformation substantially over the course of the trajectory. The conformational rearrangements appeared to be controlled by interactions of the OγH group. Initially hydrogen-bonded to Arg254, it sampled other bonding partners, including water molecules associated with Tyr272–OH and the Glu102 carboxylate (see Fig. S2, ESI†). The conformational mobility of the THR head was associated with a looser interaction between its substrate ammonium group and Glu102. Instead, Glu102 formed a salt bridge with nearby Arg254. Concomitantly with cleaving the NH3+–Glu102 salt bridge, the THR head group rotated about the C2–C3 bond, which re-oriented the OH and methyl groups attached to C3 compared to the other cases (see Fig. 3). In the equilibrated MD structure, the THR OH group hydrogen-bonded to the free carboxylate tail of 2OG, which rotated towards the substrate head. (For the other substrates, the 2OG carboxylate is part of a dynamic hydrogen-bonding network involving Arg248, Lys106, Thr113, and Ser237; see Fig. S3, ESI.†) Overall, the THR complex differs from the other docked and MD-equilibrated structures in several important respects: (i) instead of the direct, strong salt bridge between the substrate ammonium and Glu102, there is a looser, water-mediated interaction; (ii) the head group with the reacting methyl adopts a different rotamer; (iii) the substrate head as a whole is placed slightly less deeply into the active-site cavity and further away from the iron centre.
Modelling the [Fe![[double bond, length as m-dash]](https://www.rsc.org/images/entities/h3_char_e001.gif) O] intermediate
O] intermediate
Having generated representative structures of enzyme–substrate complexes of intermediate A, we sought to “fast-forward” to the [Fe![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O] intermediate D. The aim was to use MD to generate full models of intermediate D, considering a series of structural isomers for the iron complex and exploring to what extent they could be assessed based on simple structural criteria.
O] intermediate D. The aim was to use MD to generate full models of intermediate D, considering a series of structural isomers for the iron complex and exploring to what extent they could be assessed based on simple structural criteria.
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/b_char_e001.gif) O] model complexes.
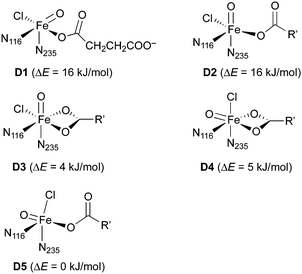
For the iron(IV)–oxido (“ferryl”) complex D (in the quintet state, 5D), several geometrical and linkage isomers are conceivable (see Scheme 5), even when considering the restraint that the protein-derived imidazole ligands must be cis to one another. We built small model complexes (with 5-methylimidazole representing the histidine imidazoles) and optimised them at the DFT level. If the succinate carboxylate is chelating, creating an octahedral coordination geometry, two geometrical isomers are possible, with either the oxido (D3) or the chlorido (D4) ligand trans to N235 (and thus pointing “up” towards the substrate in the full model). If the carboxylate is monodentate, the resulting pentacoordinate isomers (D1, D2, D5) adopt structures that are in-between trigonal-bipyramidal and square-pyramidal.‡76 The oxido ligand can be trans to either imidazole (pointing away from the substrate in D1; towards it in D2) or it can be trans to carboxylate (D5). (Note that D1 and D2 are enantiomers but for the internal conformation/orientation of the imidazole and succinate. Outside the protein environment, they are thus chemically identical.) Energetically, all these isomers are easily accessible: the least stable (D1/D2) is only 16 kJ mol−1 higher in energy than the most stable (D5). In the protein environment, such modest energy differences can easily be compensated for, e.g., by hydrogen bonding. We conclude that the iron complex on its own is structurally flexible and its geometry governed by the protein environment, rather than by intrinsic preferences. We cannot exclude any of the iron–oxido structures at this stage.
O] model complexes.
For the iron(IV)–oxido (“ferryl”) complex D (in the quintet state, 5D), several geometrical and linkage isomers are conceivable (see Scheme 5), even when considering the restraint that the protein-derived imidazole ligands must be cis to one another. We built small model complexes (with 5-methylimidazole representing the histidine imidazoles) and optimised them at the DFT level. If the succinate carboxylate is chelating, creating an octahedral coordination geometry, two geometrical isomers are possible, with either the oxido (D3) or the chlorido (D4) ligand trans to N235 (and thus pointing “up” towards the substrate in the full model). If the carboxylate is monodentate, the resulting pentacoordinate isomers (D1, D2, D5) adopt structures that are in-between trigonal-bipyramidal and square-pyramidal.‡76 The oxido ligand can be trans to either imidazole (pointing away from the substrate in D1; towards it in D2) or it can be trans to carboxylate (D5). (Note that D1 and D2 are enantiomers but for the internal conformation/orientation of the imidazole and succinate. Outside the protein environment, they are thus chemically identical.) Energetically, all these isomers are easily accessible: the least stable (D1/D2) is only 16 kJ mol−1 higher in energy than the most stable (D5). In the protein environment, such modest energy differences can easily be compensated for, e.g., by hydrogen bonding. We conclude that the iron complex on its own is structurally flexible and its geometry governed by the protein environment, rather than by intrinsic preferences. We cannot exclude any of the iron–oxido structures at this stage.
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/b_char_e001.gif) O] intermediate.
We performed MD simulations for all 15 combinations of substrates (THR, ABA, NVA) and isomers D1–D5. A simple measure was used to judge the viability of the equilibrated structures to act as reactive intermediate: the “reaction distances” between the oxido ligand and the nearest abstractable hydrogen of the substrate (dOH) and between the chlorido ligand and the reacting carbon (dCCl); see Fig. 4. The reaction distances are tabulated in Table 3.
O] intermediate.
We performed MD simulations for all 15 combinations of substrates (THR, ABA, NVA) and isomers D1–D5. A simple measure was used to judge the viability of the equilibrated structures to act as reactive intermediate: the “reaction distances” between the oxido ligand and the nearest abstractable hydrogen of the substrate (dOH) and between the chlorido ligand and the reacting carbon (dCCl); see Fig. 4. The reaction distances are tabulated in Table 3.
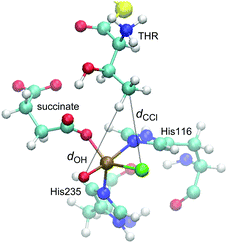 | ||
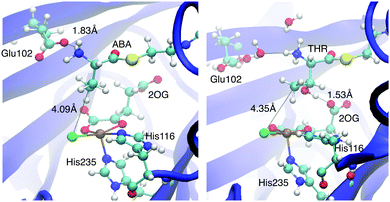
| Fig. 4 Representative snapshot from the MD trajectory of THR-D1, illustrating the “reaction distances”, dOH and dCCl. | ||
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O] isomer combinations. For THR, the group hydrogen-bonded to THR–OγH is also listed. For NVA, the values for the two reactive carbon centres C4 and C5 are listed separately. Values below/above the threshold of 5 Å are highlighted in green/red; the shortest viable dOH for each substrate is marked in bold
O] isomer combinations. For THR, the group hydrogen-bonded to THR–OγH is also listed. For NVA, the values for the two reactive carbon centres C4 and C5 are listed separately. Values below/above the threshold of 5 Å are highlighted in green/red; the shortest viable dOH for each substrate is marked in bold
As in the simulations with intermediate A before, the position and conformation of the THR head was again controlled by the interactions of its hydroxyl group (see Fig. S6, ESI†). In THR-D2 and THR-D3, where the oxido ligand points “up” towards the substrate, the OγH group is hydrogen-bonding to the oxido oxygen, which leads to a short dOH distance but relatively long dCCl distance. By contrast, in THR-D4 and THR-D5, where the chloride is pointing “up”, OγH instead hydrogen-bonded to the carboxylate tail of the succinate, as it did to 2OG in THR-A (Fig. 3, right); this results in larger reaction distances. In THR-D1, we observed two stable conformations of the substrate head: OγH was hydrogen-bonding either to the succinate tail carboxylate, like in THR-D4 and THR-D5, or to the free arm of the succinate head carboxylate (as shown in Fig. 4). The latter arrangement leads to relatively short values for both dOH and dCCl.
ABA also showed similar conformational behaviour in the simulations with D as it did with A, which in this case means that it essentially maintained the position and conformation already adopted in docking. This conformation affords relatively short reaction distances (see Table 3). The only exception was ABA-D4, where the substrate head broke free of the hydrophobic pocket in which it otherwise sits, without finding a stable conformation over the course of the simulation (see Fig. S7, ESI†).
Like ABA, also NVA largely kept the same conformation in the simulations with D, with the ammonium–Glu102 salt bridge being maintained throughout. However, the extra methylene group of NVA introduces an additional degree of freedom (i.e., rotation about C3–C4), which affects the positions of the reacting carbons C4 and C5. Two C3–C4 rotamers were observed in all NVA simulations (except for NVA-D3, which yielded a single rotamer), which remained stable over extended periods, with occasional switches between them (see Fig. S8, ESI†). At least one of the rotamers afforded relatively short reaction distances with respect to C5 in all cases (Table 3 lists the values for the more favourable rotamer in each case). Consistent with a more facile reaction at C5, reaction distances to C4 are generally longer.
We applied a very simple criterion to assess the viability of the various structural models: a substrate–isomer combination was deemed viable if both reaction distances were below 5 Å, the rationale being that if either distance is too large, the reaction would not be able to proceed without further conformational changes. As a secondary criterion, we preferred shorter reaction distances to longer ones. From this distance-based analysis, we conclude that D1 is the most likely intermediate for THR; D2 or possibly D3 (which both have the oxido ligand pointing towards the substrate) for ABA; D2 for NVA reacting at C4; and D2 or D3 for NVA reacting at C5.
These conclusions, although obtained from a purely classical modelling protocol (i.e., docking followed by MD) and a simple analysis, are nevertheless pertinent. They indicate that the [Fe![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O] intermediate is D1 for THR (five-coordinate, oxido pointing away) and D2 for ABA and NVA (five-coordinate, oxido pointing “up”); for the latter substrates the second arm of the carboxylate may be coordinated (D3). Isomers with chloride pointing “up” can be excluded. These findings agree in essence with Wong et al.'s,22 obtained from sophisticated NRVS experiments and DFT calculations on cluster models. They concluded that the [Fe
O] intermediate is D1 for THR (five-coordinate, oxido pointing away) and D2 for ABA and NVA (five-coordinate, oxido pointing “up”); for the latter substrates the second arm of the carboxylate may be coordinated (D3). Isomers with chloride pointing “up” can be excluded. These findings agree in essence with Wong et al.'s,22 obtained from sophisticated NRVS experiments and DFT calculations on cluster models. They concluded that the [Fe![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O] intermediate must be pentacoordinate and identified D1 as the isomer in the reaction with THR. For NVA (which was not investigated experimentally but included in the modelling), they proposed isomer D2; ABA was not considered in that study.
O] intermediate must be pentacoordinate and identified D1 as the isomer in the reaction with THR. For NVA (which was not investigated experimentally but included in the modelling), they proposed isomer D2; ABA was not considered in that study.
O2 activation pathway
To validate the conclusions on the structure of the pivotal [Fe![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O] species, we embarked on a full QM/MM study of the O2 activation and decarboxylation steps A → D on the S = 1, 2, and 3 surfaces. Given the challenges posed by the electronic structures of the iron–oxygen species involved, we were not seeking to resolve quantitatively all the details along the activation pathway. Rather, we focused on tracing the essential energetic and structural features and, primarily, on the structure of the “end point”, that is, the [Fe
O] species, we embarked on a full QM/MM study of the O2 activation and decarboxylation steps A → D on the S = 1, 2, and 3 surfaces. Given the challenges posed by the electronic structures of the iron–oxygen species involved, we were not seeking to resolve quantitatively all the details along the activation pathway. Rather, we focused on tracing the essential energetic and structural features and, primarily, on the structure of the “end point”, that is, the [Fe![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O] intermediate in the quintet state, 5D.
O] intermediate in the quintet state, 5D.
Table 4 summarises relative energies and spin populations of the O2 complexes B; additional structural data are provided in Fig. S10 and Table S8 (ESI†). THR-B and ABA-B have a septet ground state, the triplet and quintet states lying 40–50 kJ mol−1 higher in energy. For NVA-B, the quintet was the only stable state. Electronically, these complexes are best described as Fe(III)–superoxido (O2˙−) complexes, with the unpaired d-electrons on the iron (one, three, and five in the S = 1, 2, 3 state, respectively) ferromagnetically coupling to the superoxide radical (see Fig. S11, ESI†). (In the complexes with qu(Fe) ≈ 4.2, an additional ca. 0.5 majority spins are localised on the other directly bonded ligand atoms, mostly chloride; these bring the “iron” spin count to nearly five.) NVA-5B differs from the other quintet complexes by having five, instead of three, unpaired d-electrons, antiferromagnetically coupled to O2˙−. THR-3B is an exception altogether in that it resembles more closely an Fe(II)–3O2 adduct, with four unpaired spins on iron antiferromagnetically coupling to the neutral triplet dioxygen. The differences in electronic structure are reflected in the metal–ligand distances (see Table S8, ESI†), the Fe–Op bond being particularly sensitive to the number of unpaired electrons on iron.
| Substrate | S/ℏ | ΔE/kJ mol−1 | q u/(ℏ/2) | ||
|---|---|---|---|---|---|
| Fe | Op | Od | |||
| a THR-3B lost O2 during the def2-TZVP optimisations; values refer to the def2-TZVP single point at the def2-SVP optimised structure. b NVA-B was stable only for S = 2. | |||||
| THR | 1a | 44 | 3.37 | −0.73 | −0.81 |
| 2 | 50 | 2.91 | 0.38 | 0.52 | |
| 3 | 0 | 4.17 | 0.63 | 0.54 | |
| ABA | 1 | 50 | 1.09 | 0.49 | 0.50 |
| 2 | 41 | 2.93 | 0.37 | 0.47 | |
| 3 | 0 | 4.14 | 0.66 | 0.63 | |
| NVA | 2 | —b | 4.15 | −0.22 | −0.49 |
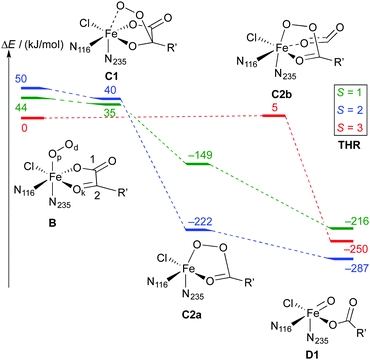
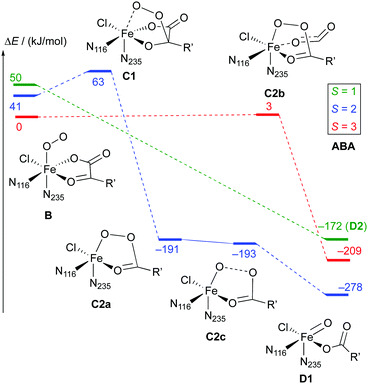
As is to be expected from the different electronic structures of the O2 complexes, the subsequent O2 activation/decarboxylation proceeds via different routes on the different spin surfaces. Schemes 6 and 7 show the reaction profiles for the path B → D on the S = 1, 2, 3 surfaces with THR and ABA substrates, respectively. For NVA, where only the quintet state was stable, we identified the following sequence of intermediates (with relative energies in kJ mol−1):
| 5B (0) → 5C2a (−183) → 5D1 (−240) |
Representative structures of the intermediates are shown in Fig. 5; structural parameters for all the intermediates are collated in Table S10 (ESI†); and the energy profiles of the coordinate scans are plotted in Fig. S13–S15 (ESI†). Fig. S16 (ESI†) shows the structure of the favoured [Fe![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O] species 5D1 for the three substrates.
O] species 5D1 for the three substrates.
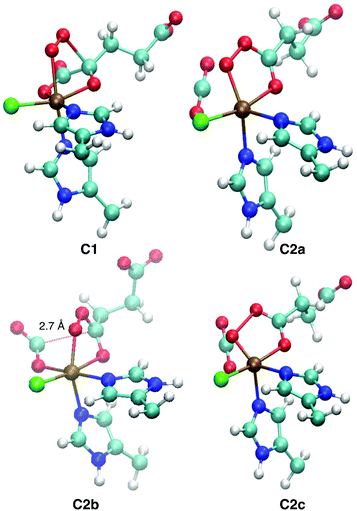 | ||
| Fig. 5 QM/MM-optimised structures of the intermediates encountered on the O2 activation pathway. C1, C2a, and C2c are taken from ABA (S = 2), C2b from ABA (S = 3). Structural parameters are tabulated in Table S10 (ESI†). | ||
Broadly speaking, two main variants of the activation pathway can be discerned; one occurring on the triplet or quintet surfaces (“low-spin”), the other on the septet surface (“high-spin”). The “low-spin” mechanism proceeds from the Fe(III)–superoxido complex 3,5B (or the Fe(II)–dioxygen complex in case of THR-3B) via nucleophilic attack of Od on the keto carbon (C2) of the 2OG ligand, forming a peroxy-bridged intermediate 3,5C1. In this intermediate, the C1–C2 bond of 2OG and also the Op–Od bond are still intact. The Fe–Ok bond has shortened, reflecting the change of the oxygen from neutral keto to a (formal) oxyanion.
In 5C1 (but not 3C1), the Fe–Op bond is significantly lengthened. Structure C1 was a stable minimum for THR (S = 1, 2) and ABA (S = 2), but was not found for NVA (S = 2).
C1 decays by cleavage of the C1–C2 bond (i.e., decarboxylation), which is strongly exothermic and leads to the Fe(II)–peroxysuccinate complex C2a, which was identified for all three substrates on the S = 2 surface and also for THR (S = 1). C2a still has an intact peroxy Op–Od bond. One-electron reduction of this bond produces the Fe(III) complex C2c. 5C2c was a stable minimum on the quintet surface for all three substrates when optimised with the smaller def2-SVP basis set. Re-optimising with def2-TZVP removed this minimum, leading directly to 5D1, except for ABA, where ABA-5C2c was stable also with def2-TZVP. This indicates that the minimum around 5C2c, where it exists, is very shallow.
For THR (S = 1, 2), ABA (S = 2), and NVA (S = 2), the final structure of the pathway was the oxido complex 3,5D1. The only exception was ABA (S = 1), which yielded the oxido isomer ABA-3D2 directly from ABA-3B, without any intermediates along the pathway.
The “high-spin” mechanism, found for THR and ABA (S = 3), proceeds from 7B again by attack of Od onto C2. Concomitantly, the C1–C2 bond is cleaved; however, the incipient CO2 does not fully dissociate but remains weakly coordinated to the iron in the resulting intermediate 7C2b. 7C2b structurally resembles 3,5C2a, featuring a peroxysuccinate moiety with regular Fe–Op and Op–Od bonds. However, 7C2b is electronically and energetically a rather different species: the CO2 moiety has radical anion character and the iron centre is oxidised to Fe(III). Energetically, 7C2b is only a few kJ mol−1 higher in energy than the initial superoxido complex. Only in the final step of the “high-spin” mechanism is the O–O bond cleaved, fully oxidising the CO2, which dissociates, and yielding 7D1. This step is strongly exothermic.
Taking these results at face value, the most likely pathway for the formation of the oxido intermediate proceeds on the septet surface: 7B undergoes facile nucleophilic addition to form 7C2b, which reacts (in what probably is the rate-determining step) to 5D1, either via the intermediacy of 7D1 or in a concerted reaction/spin-conversion step. Alternatively, 7C2b may rearrange/spin-convert to 5C2a, from where the reaction proceeds on the quintet surface, that is, by facile O–O cleavage (possibly via5C2c) to 5D1.
This mechanistic scenario agrees well with the conclusions of a recent study by Wójcik et al.,77 who compared a range of mechanistic variants proposed in the literature78–80 for the O2 activation in NHFe/2OG dependent hydroxylases (which have a 2-His-1-Asp/Glu facial triad). They carefully searched for and characterised minima, transition states, and minimum-energy crossing points, using a small QM model at the B3LYP-D3/cc-pVTZ level, validated against CCSD(T)-F12. Their preferred mechanism proceeds on the quintet surface via5B → 5C2a → 5D (with a possible, but slightly less favourable “detour” via5C1), thus resembling our “low-spin” mechanism. However, they found that a “high-spin” (septet) pathway was nearly as favourable. Equally as relevant for our purposes is their conclusion that B3LYP-D3 provides a faithful representation of the delicate spin-state energetics in these systems.
While those findings lend support to our approach and results on the O2 activation mechanism in SyrB2, one should keep in mind that the fine detail of the mechanism – the exact topographies of the energy surfaces of the different spin states – is very sensitive to the choice of method and model. This is illustrated, e.g., by the fact that the existence of intermediate 5C2c depends on the basis set; that is, a seemingly small, “technical” change, which might ordinarily be expected to have a modest effect on the relative energies, qualitatively alters the character of the potential-energy surface.
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O] intermediates in SyrB2 and its homologue CytC3 are experimentally accessible by 57Fe Mössbauer spectroscopy, which is sensitive to the electronic structure and the immediate chemical environment of the iron centre.81 The spectra suggest that two different [Fe
O] intermediates in SyrB2 and its homologue CytC3 are experimentally accessible by 57Fe Mössbauer spectroscopy, which is sensitive to the electronic structure and the immediate chemical environment of the iron centre.81 The spectra suggest that two different [Fe![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O] species are present in equilibrium in these enzymes.20,21 As Mössbauer spectroscopic parameters (isomer shifts, δ, and quadrupole splittings, ΔEQ) are relatively straightforward to calculate,72,82 they have been used to evaluate computationally derived models of [Fe
O] species are present in equilibrium in these enzymes.20,21 As Mössbauer spectroscopic parameters (isomer shifts, δ, and quadrupole splittings, ΔEQ) are relatively straightforward to calculate,72,82 they have been used to evaluate computationally derived models of [Fe![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O] species in SyrB226 and other NHFe enzymes.81,83,84 We therefore calculated Mössbauer parameters for the full QM/MM models of the favoured [Fe
O] species in SyrB226 and other NHFe enzymes.81,83,84 We therefore calculated Mössbauer parameters for the full QM/MM models of the favoured [Fe![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O] intermediates 5D1 in presence of substrates (see Table 5). For comparison, the table also lists the values calculated by Borowski et al.26 for their six-coordinate [Fe
O] intermediates 5D1 in presence of substrates (see Table 5). For comparison, the table also lists the values calculated by Borowski et al.26 for their six-coordinate [Fe![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O] models (corresponding to D3 and D4 in our notation) as well as the experimental values in presence of THR and ABA.21
O] models (corresponding to D3 and D4 in our notation) as well as the experimental values in presence of THR and ABA.21
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O] species in SyrB2 in presence of different substrates
O] species in SyrB2 in presence of different substrates
| δ/(mm s−1) | |ΔEQ|/(mm s−1) | ||
|---|---|---|---|
| a Calculated with B3LYP/CP(PPP) for the full QM/MM models in this work. δ values were obtained using the linear fits of ref. 73 and [ref. 74]. b From ref. 26. Calculated with B3LYP/CP(PPP) for first-shell models extracted from a larger cluster. δ values were obtained using the linear fit of ref. 73. c From ref. 21 (ESI). The ratio of the two species present is given in brackets. | |||
| THR-5D1 | Calcda | 0.19 [0.22] | 1.12 |
| ABA-5D1 | Calcda | 0.15 [0.18] | 1.11 |
| NVA-5D1 | Calcda | 0.17 [0.20] | 1.32 |
| THR-5D3 | Calcdb | 0.27 | 1.31 |
| THR-5D4 | Calcdb | 0.21 | 0.94 |
| THR-5D | Exptlc | 0.30, 0.23 (4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) 1) |
1.09, 0.76 |
| ABA-5D | Exptlc | 0.28, 0.24 (7![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) 1) |
0.99, 0.66 |
While the accuracy of isomer shifts calculated with a particular fit is typically very good (∼0.1 mm s−1),73,74 the values obtained using different fits can vary by several tenths mm s−1, as illustrated in Table 5. Quadrupole splittings are predicted less accurately, to within about 0.2–0.3 mm s−1.74 Considering these error bars, the isomer shift calculated for THR-5D1 agrees well with the experimental value for the minority species. However, for ABA-5D1, which is calculated to have a significantly smaller δ, the match is much less good. On the other hand, the calculated quadrupole splittings for both THR-5D1 and ABA-5D1 agree with the experimental values for the majority species. The Mössbauer data thus neither clearly corroborate nor exclude the identification of the [Fe![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O] species with structure D1. By contrast, the Mössbauer parameters calculated in ref. 26 for the six-coordinate isomers D3 and D4 are in remarkable agreement with experiment, which would support the assignment of the two species seen experimentally as D3 and D4. However, these structures are not consistent with the NRVS data.22 At this stage, it is difficult to reconcile the Mössbauer data with the conclusions from the NRVS/computational22 study and the present QM/MM results.
O] species with structure D1. By contrast, the Mössbauer parameters calculated in ref. 26 for the six-coordinate isomers D3 and D4 are in remarkable agreement with experiment, which would support the assignment of the two species seen experimentally as D3 and D4. However, these structures are not consistent with the NRVS data.22 At this stage, it is difficult to reconcile the Mössbauer data with the conclusions from the NRVS/computational22 study and the present QM/MM results.
Discussion
Beyond the detail of the O2 activation/decarboxylation steps obtained from the QM/MM calculations, it is important to highlight the broader picture. All the pathways B → D, irrespective of spin state, substrate, etc., share four essential features: (i) the stable product is the oxido complex in the quintet state, 5D. (ii) In particular, structure 5D1 is obtained in all but one case. (iii) The O2 activation/decarboxylation reaction is strongly exothermic, by ca. −300 kJ mol−1. (iv) There are neither high-lying nor strongly stabilised intermediates between B and D that would impede catalytic turnover. These key features are in overall excellent agreement with experiment: 5D forms readily and spontaneously once O2 and substrate are present; and THR-5D1 has been identified as the active oxido species by the combined NRVS/computational study.22 Moreover, the QM/MM results directly validate, and are corroborated by, the conclusions of the classical modelling for the native substrate THR. For ABA and NVA, the structures obtained from the QM/MM pathways (i.e., 5D1) are consistent with the classical modelling in the sense that D1 lies in the “green zone” for these substrates (see Table 3), although D2 was favoured based on the classical results alone. Notably, only two of the conceivable isomers of D, namely D1 and D2, have emerged as the favoured structure for any of the cases investigated herein.While our results agree with Wong et al.'s22 on the central question of the structure of the [Fe![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O] intermediate for THR, it is instructive to compare their (computational) findings about the mechanism leading to its formation. They suggested that the substrate amino group played a significant role in controlling the structure of D. (Note that in their model, the substrate amino group and also the Glu102 side-chain are neutral.) For THR, both OγH and the amino group were hydrogen-bonded to Glu102, which held the amino group away from the peroxy oxygens in intermediates C, allowing the oxido oxygen to adopt the position trans to His116, thus forming D1. By contrast, for NVA, the amino group hydrogen-bonded to Op during O2 activation, holding it in the position trans to His235, which led to the formation of D2.
O] intermediate for THR, it is instructive to compare their (computational) findings about the mechanism leading to its formation. They suggested that the substrate amino group played a significant role in controlling the structure of D. (Note that in their model, the substrate amino group and also the Glu102 side-chain are neutral.) For THR, both OγH and the amino group were hydrogen-bonded to Glu102, which held the amino group away from the peroxy oxygens in intermediates C, allowing the oxido oxygen to adopt the position trans to His116, thus forming D1. By contrast, for NVA, the amino group hydrogen-bonded to Op during O2 activation, holding it in the position trans to His235, which led to the formation of D2.
In our simulations, however, the direct ammonium–Glu102 interaction in THR is broken during the MD simulations, facilitated by the other interactions of OγH. In NVA, on the other hand, the ammonium–Glu102 salt bridge is maintained throughout, even when the oxido oxygen is well accessible as a bonding partner (in D2 or D3). We did not observe hydrogen-bonding between the ammonium and either of the peroxy oxygens in any of the systems. Considering the sensitivity of the mechanism, it is therefore notable that despite the differences in structure and setup (QM cluster model vs. full QM/MM, neutral vs. ionised residues, BP86/def2-SVP vs. B3LYP/def2-TZVP), the primary outcome (i.e., the formation of D1) is the same.
The QM/MM study by Shaik and co-workers,29 which started from an MD-equilibrated structure of THR-D3, considered isomerisation to D1 and D4, but the subsequent hydrogen-abstraction was found to proceed from the initial D3. The resulting [FeCl(OH)] species E was proposed to isomerise before transferring preferably the Cl onto the substrate. This is compatible with the present study in so far as D1, being the primary product of O2 activation/decarboxylation, could isomerise to D3 before the hydrogen-abstraction step. However, unless H-abstraction was faster than the D1 → D3 conversion (which it is not according to ref. 29), it is difficult to reconcile this scenario with Wong et al.'s NRVS results,22 which identify the (relatively) long-lived species D as being D1.
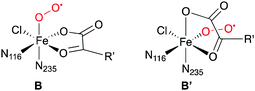
Another interesting comparison is with an experimental study on the structure of the O2-bound complex B that appeared while this work was already in progress. Using advanced EPR techniques and NO as a non-reactive surrogate of O2, Martinie et al.85 determined distances and angles between the NO nitrogen (standing for Op), iron, and specific hydrogens of the substrates THR, ABA, and NVA in SyrB2. While the experimental distances agree well with the structures of the QM/MM-optimised complexes B, the angles do not (see Table S9 and Fig. S12, ESI†). Based on simple docking models, Martinie et al. proposed that O2 might not bind trans to His235, i.e., at the position of the water present in the X-ray structure of the holoprotein, but trans to His116. Substrate binding, water dissociation, or O2 binding would thus trigger a rearrangement, resulting in structure B′. Precedent for such a rearrangement exists in clavaminate synthase, a 2-His-1-Asp NHFe/2OG enzyme.86
However, to the best of our knowledge, all mechanistic models of O2 activation in NHFe/2OG enzymes, the halogenases in particular, are based on structure B. (Note that B and B′ are enantiomers, so models that do not include any environment residues would not be affected.) This raises interesting new questions about the structural and electronic course of O2 activation in these enzymes.
Conclusions
In order to rationalise at the atomic level the intriguing regio- and chemoselectivity patterns for different substrates in the chlorination and hydroxylation reactions catalysed by SyrB2, it is crucial to understand the structure of the pivotal [Fe![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O] intermediate D in the presence of the substrate. The course and outcome of the subsequent hydrogen-abstraction and Cl/OH rebound steps depend on the exact positioning of the reacting iron-bound ligands relative to the substrate C–H bond.29–31 The elucidation of this structure has been impeded by a number of factors: the lack of an X-ray structure with bound substrate, the structural flexibility of the substrate and the iron complex, and the interactions of the complex with the protein environment.
O] intermediate D in the presence of the substrate. The course and outcome of the subsequent hydrogen-abstraction and Cl/OH rebound steps depend on the exact positioning of the reacting iron-bound ligands relative to the substrate C–H bond.29–31 The elucidation of this structure has been impeded by a number of factors: the lack of an X-ray structure with bound substrate, the structural flexibility of the substrate and the iron complex, and the interactions of the complex with the protein environment.
In this contribution, we have approached the problem by a combination of classical and QM/MM modelling. In addition to the native substrate THR, we included ABA and NVA, which have been used in previous experimental and computational studies of SyrB2. Using molecular docking and classical MD simulations, we constructed complete atomistic, equilibrated models of SyrB2 in complex with these substrates and five isomers of D. We evaluated each substrate–isomer combination based on a simple “reaction distance” criterion and identified isomers D1 and D2 to be likely intermediates.
We also built equilibrated models of the substrate-bound resting state A. These served as starting points for a QM/MM investigation to identify the intermediates along the O2 activation/decarboxylation pathway B → D for all three substrates on the S = 1, 2, and 3 potential-energy surfaces. The primary outcome is that all pathways (with one exception) yield the [Fe![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O] isomer D1 in the quintet state, in which the oxido oxygen points away from the substrate. The details of the O2 activation/decarboxylation steps are very sensitive to the choice of method and model, and their full elucidation may require further developments, especially in the area of multi-reference methods capable of treating larger systems.9,87 However, in the meantime, the present conclusions appear sufficiently robust to inform further computational and experimental efforts aimed at uncovering the factors that control the unique reactivity and selectivity of SyrB2 and related NHFe halogenases.
O] isomer D1 in the quintet state, in which the oxido oxygen points away from the substrate. The details of the O2 activation/decarboxylation steps are very sensitive to the choice of method and model, and their full elucidation may require further developments, especially in the area of multi-reference methods capable of treating larger systems.9,87 However, in the meantime, the present conclusions appear sufficiently robust to inform further computational and experimental efforts aimed at uncovering the factors that control the unique reactivity and selectivity of SyrB2 and related NHFe halogenases.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
We are grateful to Andrew Jarnuczak for preparing the initial SyrB2 structure. G. R. was supported by a Doctoral Training Grant from the EPSRC (EP/P504937/1, EP/J500434/1).Notes and references
- J. L. R. Anderson and S. K. Chapman, Mol. BioSyst., 2006, 2, 350–357 RSC.
- K.-H. van Pée, C. J. Dong, S. Flecks, J. Naismith, E. P. Patallo and T. Wage, Adv. Appl. Microbiol., 2006, 59, 127–157 Search PubMed.
- F. H. Vaillancourt, E. Yeh, D. A. Vosburg, S. Garneau-Tsodikova and C. T. Walsh, Chem. Rev., 2006, 106, 3364–3378 CrossRef CAS PubMed.
- D. Galonić Fujimori and C. T. Walsh, Curr. Opin. Chem. Biol., 2007, 11, 553–560 CrossRef PubMed.
- C. S. Neumann, D. Galonić Fujimori and C. T. Walsh, Chem. Biol., 2008, 15, 99–109 CrossRef CAS PubMed.
- L. C. Blasiak and C. L. Drennan, Acc. Chem. Res., 2008, 42, 147–155 CrossRef PubMed.
- C. Wagner, M. El Omari and G. M. König, J. Nat. Prod., 2009, 72, 540–553 CrossRef CAS PubMed.
- A. Butler and M. Sandy, Nature, 2009, 460, 848–854 CrossRef CAS PubMed.
- H. M. Senn, Front. Chem., 2014, 2, 15 Search PubMed.
- K. H. van Pée, Curr. Org. Chem., 2012, 16, 2583–2597 CrossRef.
- V. Weichold, D. Milbredt and K.-H. van Pée, Angew. Chem., Int. Ed., 2016, 55, 6374–6389 CrossRef CAS PubMed.
- V. Agarwal, Z. D. Miles, J. M. Winter, A. S. Eustáquio, A. A. El Gamal and B. S. Moore, Chem. Rev., 2017, 117, 5619–5674 CrossRef CAS PubMed.
- D. R. Smith, S. Grüschow and R. J. Goss, Curr. Opin. Chem. Biol., 2013, 17, 276–283 CrossRef CAS PubMed.
- S. Brown and S. E. O'Connor, ChemBioChem, 2015, 16, 2129–2135 CrossRef CAS PubMed.
- F. H. Vaillancourt, J. Yin and C. T. Walsh, Proc. Natl. Acad. Sci. U. S. A., 2005, 102, 10111–10116 CrossRef CAS PubMed.
- L. C. Blasiak, F. H. Vaillancourt, C. T. Walsh and C. L. Drennan, Nature, 2006, 440, 368–371 CrossRef CAS PubMed.
- A. J. Mitchell, Q. Zhu, A. O. Maggiolo, N. R. Ananth, M. L. Hillwig, X. Liu and A. K. Boal, Nat. Chem. Biol., 2016, 12, 636–640 CrossRef CAS PubMed.
- J. M. Bollinger, Jr., W.-C. Chang, M. L. Matthews, R. J. Martinie, A. K. Boal and C. Krebs, in 2-Oxoglutarate-Dependent Oxygenases, ed. R. P. Hausinger and C. J. Schofield, Royal Society of Chemistry, Cambridge, UK, 2015, pp. 95–122 10.1039/9781782621959-00095.
- D. Galonić Fujimori, E. W. Barr, M. L. Matthews, G. M. Koch, J. R. Yonce, C. T. Walsh, J. M. Bollinger, Jr., C. Krebs and P. J. Riggs-Gelasco, J. Am. Chem. Soc., 2007, 129, 13408–13409 CrossRef PubMed.
- D. P. Galonić, E. W. Barr, C. T. Walsh, J. M. Bollinger, Jr. and C. Krebs, Nat. Chem. Biol., 2007, 3, 113–116 CrossRef PubMed.
- M. L. Matthews, C. M. Krest, E. W. Barr, F. H. Vaillancourt, C. T. Walsh, M. T. Green, C. Krebs and J. M. Bollinger, Biochemistry, 2009, 48, 4331–4343 CrossRef CAS PubMed.
- S. D. Wong, M. Srnec, M. L. Matthews, L. V. Liu, Y. Kwak, K. Park, C. B. Bell, III, E. E. Alp, J. Zhao, Y. Yoda, S. Kitao, M. Seto, C. Krebs, J. M. Bollinger, Jr. and E. I. Solomon, Nature, 2013, 499, 320–323 CrossRef CAS PubMed.
- S. Pandian, M. A. Vincent, I. H. Hillier and N. A. Burton, Dalton Trans., 2009, 6201–6207 RSC.
- S. P. de Visser and R. Latifi, J. Phys. Chem. B, 2009, 113, 12–14 CrossRef CAS PubMed.
- H. J. Kulik, L. C. Blasiak, N. Marzari and C. L. Drennan, J. Am. Chem. Soc., 2009, 131, 14426–14433 CrossRef CAS PubMed.
- T. Borowski, H. Noack, M. Radoń, K. Zych and P. E. M. Siegbahn, J. Am. Chem. Soc., 2010, 132, 12887–12898 CrossRef CAS PubMed.
- H. J. Kulik and C. L. Drennan, J. Biol. Chem., 2013, 288, 11233–11241 CrossRef CAS PubMed.
- M. L. Matthews, C. S. Neumann, L. A. Miles, T. L. Grove, S. J. Booker, C. Krebs, C. T. Walsh and J. M. Bollinger, Jr., Proc. Natl. Acad. Sci. U. S. A., 2009, 106, 17723–17728 CrossRef CAS PubMed.
- J. Huang, C. Li, B. Wang, D. A. Sharon, W. Wu and S. Shaik, ACS Catal., 2016, 6, 2694–2704 CrossRef CAS.
- M. Srnec, S. D. Wong, M. L. Matthews, C. Krebs, J. M. Bollinger, Jr. and E. I. Solomon, J. Am. Chem. Soc., 2016, 138, 5110–5122 CrossRef CAS PubMed.
- M. Srnec and E. I. Solomon, J. Am. Chem. Soc., 2017, 139, 2396–2407 CrossRef CAS PubMed.
- A. Šali and T. L. Blundell, J. Mol. Biol., 1993, 234, 779–815 CrossRef PubMed.
- Modeller, 9v8, 2010, http://www.salilab.org/modeller/.
- J. M. Word, S. C. Lovell, J. S. Richardson and D. C. Richardson, J. Mol. Biol., 1999, 285, 1735–1747 CrossRef CAS PubMed.
- J. M. Word, Reduce, v. 3.14, 2010, http://kinemage.biochem.duke.edu/software/reduce.php.
- H. Li, A. D. Robertson and J. H. Jensen, Proteins: Struct., Funct., Bioinf., 2005, 61, 704–721 CrossRef CAS PubMed.
- propKa, v. 2.0, 2008, http://www.propka.org.
- O. Trott and A. J. Olson, J. Comput. Chem., 2010, 31, 455–461 CAS.
- O. Trott and A. J. Olson, AutoDock Vina, v. 1.1.2, 2011, http://vina.scripps.edu.
- D. M. Krüger, G. Jessen and H. Gohlke, J. Chem. Inf. Model., 2012, 52, 2807–2811 CrossRef PubMed.
- B. Hess, C. Kutzner, D. van der Spoel and E. Lindahl, J. Chem. Theory Comput., 2008, 4, 435–447 CrossRef CAS PubMed.
- S. Pronk, S. Páll, R. Schulz, P. Larsson, P. Bjelkmar, R. Apostolov, M. R. Shirts, J. C. Smith, P. M. Kasson, D. van der Spoel, B. Hess and E. Lindahl, Bioinformatics, 2013, 29, 845–854 CrossRef CAS PubMed.
- E. Apol, R. Apostolov, H. J. C. Berendsen, A. van Buuren, P. Bjelkmar, R. van Drunen, A. Feenstra, G. Groenhof, P. Kasson, P. Larsson, P. Meulenhoff, T. Murtola, S. Páll, S. Pronk, R. Schulz, M. Shirts, A. Sijbers, P. Tieleman, B. Hess, D. van der Spoel and E. Lindahl, GROMACS, v. 4.5.5, 2011, http://www.gromacs.org Search PubMed.
- Y. Duan, C. Wu, S. Chowdhury, M. C. Lee, G. Xiong, W. Zhang, R. Yang, P. Cieplak, R. Luo, T. Lee, J. Caldwell, J. Wang and P. Kollman, J. Comput. Chem., 2003, 24, 1999–2012 CrossRef CAS PubMed.
- J. Wang, R. M. Wolf, J. W. Caldwell, P. A. Kollman and D. A. Case, J. Comput. Chem., 2004, 25, 1157–1174 CrossRef CAS PubMed.
- J. Wang, R. M. Wolf, J. W. Caldwell, P. A. Kollman and D. A. Case, J. Comput. Chem., 2005, 26, 114 CrossRef CAS.
- W. L. Jorgensen, J. Chandrasekhar, J. D. Madura, R. W. Impey and M. L. Klein, J. Chem. Phys., 1983, 79, 926–935 CrossRef CAS.
- U. C. Singh and P. A. Kollman, J. Comput. Chem., 1984, 5, 129–145 CrossRef CAS.
- D. A. Case, T. A. Darden, T. E. Cheatham, III, C. L. Simmerling, J. Wang, R. E. Duke, R. Luo, R. C. Walker, W. Zhang, K. M. Merz, B. Roberts, S. Hayik, A. Roitberg, G. Seabra, J. Swails, A. W. Goetz, I. Kolossváry, K. F. Wong, F. Paesani, J. Vanicek, R. M. Wolf, J. Liu, X. Wu, S. R. Brozell, T. Steinbrecher, H. Gohlke, Q. Cai, X. Ye, J. Wang, M.-J. Hsieh, G. Cui, D. R. Roe, D. H. Mathews, M. G. Seetin, R. Salomon-Ferrer, C. Sagui, V. Babin, T. Luchko, S. Gusarov, A. Kovalenko and P. A. Kollmann, AMBER 12, University of California, San Francisco, 2012, http://www.ambermd.org Search PubMed.
- A. W. Sousa da Silva, ACPYPE, rev. 7268, 2013, http://code.google.com/p/acpype.
- A. W. Sousa da Silva and W. F. Vranken, BMC Res. Notes, 2012, 5, 367 CrossRef PubMed.
- ChemShell, a Computational Chemistry Shell, v. 3.6.dev, 2014, http://www.chemshell.org.
- S. Metz, J. Kästner, A. A. Sokol, T. W. Keal and P. Sherwood, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2014, 4, 101–110 CrossRef CAS.
- TURBOMOLE, a development of University of Karlsruhe and Forschungszentrum Karlsruhe GmbH, 1989–2007, TURBOMOLE GmbH, since 2007; available from http://www.turbomole.com, V. 6.4, 2012.
- R. Ahlrichs, M. Bär, M. Häser, H. Horn and C. Kölmel, Chem. Phys. Lett., 1989, 162, 165–169 CrossRef CAS.
- M. Häser and R. Ahlrichs, J. Comput. Chem., 1989, 10, 104–111 CrossRef.
- O. Treutler and R. Ahlrichs, J. Chem. Phys., 1995, 102, 346–354 CrossRef CAS.
- J. Kästner, S. Thiel, H. M. Senn, P. Sherwood and W. Thiel, J. Chem. Theory Comput., 2007, 3, 1064–1072 CrossRef PubMed.
- S. R. Billeter, A. J. Turner and W. Thiel, Phys. Chem. Chem. Phys., 2000, 2, 2177–2186 RSC.
- J. Kästner, J. M. Carr, T. W. Keal, W. Thiel, A. Wander and P. Sherwood, J. Phys. Chem. A, 2009, 113, 11856–11865 CrossRef PubMed.
- A. D. Becke, Phys. Rev. A: At., Mol., Opt. Phys., 1988, 38, 3098–3100 CrossRef CAS.
- S. H. Vosko, L. Wilk and M. Nusair, Can. J. Phys., 1980, 58, 1200–1211 CrossRef CAS.
- C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789 CrossRef CAS.
- A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652 CrossRef CAS.
- P. J. Stephens, J. F. Devlin, C. F. Chabalowski and M. J. Frisch, J. Phys. Chem., 1994, 98, 11623–11627 CrossRef CAS.
- R. H. Hertwig and W. Koch, Chem. Phys. Lett., 1997, 268, 345–351 CrossRef CAS.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed.
- F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305 RSC.
- ORCA, V. 4.0.1.2, 2017, http://orcaforum.cec.mpg.de.
- F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 73–78 CrossRef CAS.
- F. Neese, F. Wennmohs, A. Hansen and U. Becker, Chem. Phys., 2009, 356, 98–109 CrossRef CAS.
- F. Neese, Inorg. Chim. Acta, 2002, 337, 181–192 CrossRef.
- M. Römelt, S. F. Ye and F. Neese, Inorg. Chem., 2009, 48, 784–785 CrossRef PubMed.
- M. Pápai and G. Vankó, J. Chem. Theory Comput., 2013, 9, 5004–5020 CrossRef PubMed.
- M. R. Fullone, A. Paiardini, R. Miele, S. Marsango, D. C. Gross, S. Omura, E. Ros-Herrera, M. C. Bonaccorsi di Patti, A. Laganà, S. Pascarella and I. Grgurina, FEBS J., 2012, 279, 4269–4282 CrossRef CAS PubMed.
- A. W. Addison, T. N. Rao, J. Reedijk, J. van Rijn and G. C. Verschoor, J. Chem. Soc., Dalton Trans., 1984, 1349–1356, 10.1039/dt9840001349.
- A. Wójcik, M. Radoń and T. Borowski, J. Phys. Chem. A, 2016, 120, 1261–1274 CrossRef PubMed.
- A. R. Diebold, C. D. Brown-Marshall, M. L. Neidig, J. M. Brownlee, G. R. Moran and E. I. Solomon, J. Am. Chem. Soc., 2011, 133, 18148–18160 CrossRef CAS PubMed.
- S. Ye, C. Riplinger, A. Hansen, C. Krebs, J. M. Bollinger, Jr. and F. Neese, Chem. – Eur. J., 2012, 18, 6555–6567 CrossRef CAS PubMed.
- M. R. Blomberg, T. Borowski, F. Himo, R.-Z. Liao and P. E. M. Siegbahn, Chem. Rev., 2014, 114, 3601–3658 CrossRef CAS PubMed.
- C. Krebs, J. C. Price, J. Baldwin, L. Saleh, M. T. Green and J. M. Bollinger Jr., Inorg. Chem., 2005, 44, 742–757 CrossRef CAS PubMed.
- S. Sinnecker, L. D. Slep, E. Bill and F. Neese, Inorg. Chem., 2005, 44, 2245–2254 CrossRef CAS PubMed.
- S. Sinnecker, N. Svensen, E. W. Barr, S. Ye, J. M. Bollinger, Jr., F. Neese and C. Krebs, J. Am. Chem. Soc., 2007, 129, 6168–6179 CrossRef CAS PubMed.
- X. D. Song, J. R. Lu and W. Z. Lai, Phys. Chem. Chem. Phys., 2017, 19, 20188–20197 RSC.
- R. J. Martinie, J. Livada, W. C. Chang, M. T. Green, C. Krebs, J. M. Bollinger, Jr. and A. Silakov, J. Am. Chem. Soc., 2015, 137, 6912–6919 CrossRef CAS PubMed.
- Z. H. Zhang, J. S. Ren, K. Harlos, C. H. McKinnon, I. J. Clifton and C. J. Schofield, FEBS Lett., 2002, 517, 7–12 CrossRef CAS PubMed.
- T. A. Rokob, J. Chalupský, D. Bím, P. C. Andrikopoulos, M. Srnec and L. Rulíšek, J. Biol. Inorg. Chem., 2016, 21, 619–644 CrossRef CAS PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available: Additional computational details and supplementary results. See DOI: 10.1039/c7cp05937j |
| ‡ The trigonality index τ5 is 0.65 for D1/D2 and 0.49 for D5. τ5 = (β − α)/60°, where β is the largest of the ten valence angles around a five-coordinate centre; α is the second-largest. For a perfect trigonal bipyramid, τ5 = 1 (β = 180°, α = 60°); for an ideal square pyramid, τ5 = 0 (α = β ≤ 180°). |
| This journal is © the Owner Societies 2017 |