Role of free electrons in phosphorescence in n-type wide bandgap semiconductors
Abstract
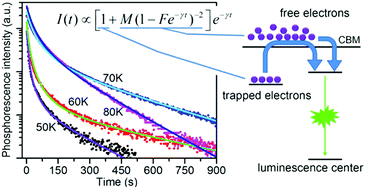
Long persistent phosphorescence is generally known as a phenomenon involving carrier traps induced by defects or impurities in crystals. In this paper, phosphorescence sustained for tens of minutes was found in intentionally undoped ZnO and it was proposed to be a universal phenomenon in wide bandgap semiconductors upon satisfying several conditions. A new model was built to understand this attractive phenomenon within the framework of the traditional trapping–detrapping model but it was modified by considering the free electrons in the conduction band as a significant contributor to the long persistent phosphorescence besides the electrons trapped by shallow donors. This model, explicitly expressed as I(t) ∝ [1 + M(1 − Fe−γt)−2]e−γt, is not only capable of giving a quantitative description of the non-exponential decay of phosphorescence in a wide temperature range but also enables one to determine the depth of shallow donors in semiconductors. The participation of free electrons in phosphorescence was further confirmed by another carefully designed experiment. Thus, this study may represent significant progress in understanding phosphorescence.
- This article is part of the themed collection: 2017 PCCP HOT Articles


 Please wait while we load your content...
Please wait while we load your content...