The role of the σ-holes in stability of non-bonded chalcogenide⋯benzene interactions: the ground and excited states

Abstract

The stability of the T-shaped and stacked complexes of benzene with methanethial (CH₂S) and methaneselone (CH₂Se) and their difluoro-, dichloro-, dibromo-derivatives is investigated in their ground and first electronic excited states by means of the SCS-ADC2 method. The origin of the stabilization in the ground state is discussed based on the results of calculations performed using the DFT-SAPT method. Calculations show that the stability of the T-shaped conformers increases upon electronic excitation, while it decreases for most of the stacked conformers. Both effects are explained by the changes in the electrostatic potential (ESP) of isolated monomers upon the electronic excitation.

---

Introduction

The character of the non-covalent interactions, including the halogen and chalcogen bonds, and their role in the molecular assembly, stability of crystal structures, properties of biological molecules and chemical reactions have been subjects of many experimental and computational studies.^1–10 Tunability and directionality of halogen bonds can be effectively utilized in the design of organic light-emitting crystals with a high phosphorescence quantum yield.^1–4,11 Halogen-bonded complexes, which involve π-electrons, were also studied as potential optoelectronic materials.^11–14 Despite the great effort made in these studies there are still many challenges remaining for a better understanding of the complexes formed by non-covalent interactions, including halogen and chalcogen bonds.

The halogen/chalcogen bonds result from the interactions between the so-called positively charged σ-holes and the negative sites, e.g. anions or a lone pair of Lewis bases. The holes correspond to the regions of a diminished electron density, which results from a high degree of polarization. Thus, σ-holes are a consequence of an anisotropic distribution of the electron density around atoms involved in covalent bonds. Upon covalent bond formation, the electron density is polarized toward the bond region, leading to a decrease of electron density in the outer part of the molecule along the extension of the covalent σ-bond.¹⁵ The same type of interaction can be formed also between the so-called π-hole and the negative site. In this case the π-hole is the region of the diminished electron density perpendicular to the molecular plane.¹⁶ The features described above are nicely illustrated by the molecule's electrostatic potential (MEP) which is usually defined at the 0.001 a.u. isodensity surface.¹⁷ Here we stress that the MEP is a physical observable. The MEP can be calculated from electronic density which can be calculated based on a theoretical model or measured experimentally.^18,19

The point with the most positive value of the electrostatic potential (ESP) characterizes the magnitude of the σ- and π-holes (V_max) and the size of the area with the positive ESP determines the size of the hole.²⁰ As discussed by Politzer et al.^21,22 the major driving force for the resulting halogen or chalcogen bonding is the electrostatic interaction between the positive σ- and π-holes and the negative site is further stabilized by polarization and dispersion.

The potential use of chalcogen bond donors in crystal engineering is not so common contrary to halogen bonds, probably due to small directionality in the case of interactions of the former. However, the examples of self-assembly of molecules via chalcogen bonds are known e.g.: benzo-2,1,3-selenadiazoles,²³ benzo-1,3-tellurazoles,²⁴ iso-tellurazole N-oxides²⁵ or organic selenocyanates.²⁶

As shown in the work of Bauza et al.²⁷ some chalcogen bond motifs are relatively frequent in the Cambridge Structural database (CSD, version 5.33 (November 2011)).²⁸ The search of C=X⋯Y (X = S, Se and Y = O, S and N, respectively) contacts closer than van der Waals radii among known X-ray structures (in the CSD, version 5.38 (November 2016) + 1 update)²⁸ shows that the most and least frequent are the C=S⋯S and C=Se⋯S contacts with the abundance of 1966 and 20, respectively. A relatively large number of 7264 C=S⋯π contacts (the π system is represented by the C₆ aromatic ring) have been found in the survey of the CSD (version 5.38 (November 2016) + 1 update).²⁹ The contacts are defined as follows: the distance between the sulfur and the closest carbon atom from the π ring is smaller than the sum of van der Waals radii +0.5 Å and the C–S⋯π centroid angle is constrained to 110°–180°. Same constraints have been applied in the survey done by Bauze et al.²⁷ Contrary to the C=S⋯π contact, the C=Se⋯π contact is quite rare with the abundance of only 266. All searches have been done using the ConQuest 1.19 program.³⁰

In recent review Mahmudov et al.³¹ pointed out the importance of the chalcogen bonds for crystal engineering and design of new materials stressing the potential of chalcogen-containing systems for the use in materials sciences. The modification of such systems by non-covalent interactions is thoroughly investigated by monitoring their properties, as subtle changes in the electronic structures can lead to dramatic changes in the properties of these nanosystems.³² Studies of the relevant models in their ground and excited states can bring insights also into their optical properties.

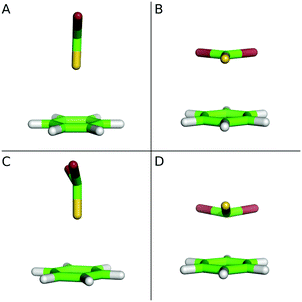
In the current study the origin of the stabilization of benzene⋯chalcogenide complexes, which includes interactions of both the σ- and π-holes^16,22,33 with the aromatic system of benzene, is investigated in their ground and excited states. The T-shaped and stacked conformers are considered (see Fig. 1). The relative stabilities of the complexes in the ground and excited states are discussed with respect to the changes in the ESPs upon excitations. This work is intended as a model study to gain insights into changes in the non-covalent chalcogen bond properties of weakly bonded complexes upon excitation and, at the same time, to perform the bonding analyses at a reliable computational level.

Fig. 1 The structures of the C₆H₆⋯CBr₂Se complex. (A) The ground (S0) state of the T-shaped conformer; (B) the ground (S0) state of the stacked conformer; (C) the excited (S1) state of the T-shaped conformer; (D) the excited (S1) state of the stacked conformer. Comparison of A vs. C and B vs. D: the pyramidalization of the CBr₂S molecule.

Calculations

The ground and first excited state gradient optimizations were performed at the spin component scaled-second order algebraic diagrammatic construction (SCS-ADC2)/def2-TZVP level.^34–36 The same levels of calculations were used also to calculate the interaction energies in the ground and excited states. The interaction energy values were corrected for basis set superposition error utilizing the counterpoise correction.³⁷ The SCS-ADC2 method is the spin component scaled variant of the ADC method, where correlation energy from electrons with the same and opposite spins is scaled by empirical parameters.^35,36 The ADC method combines diagonalization of the Hermitian secular matrix with the Raleigh–Schroedinger perturbation theory for the secular matrix elements.

The interaction energies of the ground state complexes were further analyzed performing the density functional theory – symmetry adapted perturbation theory (DFT-SAPT) decomposition, which provides an efficient approach that rationalizes interactions in terms of the physically relevant terms.^38,39

The DFT-SAPT method utilizes the many-body SAPT method for an evaluation of the interaction energy, in which the intramolecular monomer correlation is treated at the DFT level and thus decreasing the computational expense contrary to the standard double-perturbed SAPT method.

The aug-cc-pVDZ basis set^40,41 was used for the calculations. To overcome the well-known problem of underestimation of the dispersion terms calculated with the basis set of double-ζ quality the dispersion energy terms were scaled by a coefficient of 1.19. This approach is used to approximate its complete basis set (CBS) limit value.⁴² For more details about the DFT-SAPT method see ref. 39.

The ground state electrostatic potentials (ESPs) of the monomers were calculated using the HF/cc-pVTZ^40,41 level at geometries taken from optimized structures of complexes. The excited state ESPs of monomers were calculated at the CIS/cc-pVTZ⁴³ level at geometries obtained with the ground and excited state complex optimizations. The isodensity surface of the value 0.001 a.u. was used to evaluate the ESPs.¹⁷ The Cubegen utility was used to generate grid files with a point-to-point distance of 1/6 Bohr.⁴⁴ The local extrema at the potential energy surface were analyzed utilizing the Multiwfn program.^45,46 The images were rendered using the Pymol⁴⁷ and Molekel⁴⁸ programs.

The SCS-ADC2 gradient optimizations as well as interaction energy calculations were performed using Turbomole.⁴⁹ The DFT-SAPT decomposition of interaction energies was utilized in Molpro.⁵⁰

The Cartesian coordinates of the optimized geometries of the ground and first excited states for all considered noncovalent complexes are given in the ESI.†

Results and discussion

Interaction energies

The character of chalcogen interactions with the aromatic π-system in the ground and excited states was studied for benzene⋯CX₂S and benzene⋯CX₂Se complexes (X = H, F, Cl and Br) in stacked (S) and T-shaped (T) conformations (see Fig. 1). The interaction energies of the ground state complexes calculated at the SCS-ADC2 level are compared with those obtained employing the DFT-SAPT calculations in Table 1. For both T-shaped and stacked benzene⋯CX₂S and benzene⋯CX₂Se complexes the strength of the interaction increases in the row H < F < Cl < Br. The same trend was reported for the complexes of H₂Se and its halogenated analogues.⁵¹ In the case of benzene⋯CH₂S complexes the stabilization is underestimated at the SCS-ADC2 level by 13% with respect to DFT-SAPT. For other sulfur-containing species the error does not exceed 8%. The interaction energies of the most benzene⋯CX₂Se complexes are slightly underestimated, with the error not exceeding 9%. The results obtained using both methods show that the stacked complexes have a larger stability compared to T-shaped conformations, with increasing energy differences in the row F < H < Cl < Br.

Table 1 The interaction energies (E_inter; in kcal mol⁻¹) for T-shaped and stacked conformers and their ratio ΔE_inter(Stacked/T-shape) (cf. last two columns; ΔE_inter(Stacked/T-shape) = E_inter(Stacked)/E_inter(T-shape)) calculated at the SCS-ADC(2)^a and DFT-SAPT^b levels for the ground electronic state

	E inter				ΔEinter(Stacked/T-shape)
	T-shape		Stacked
	SCS-ADC(2)	DFT-SAPT	SCS-ADC(2)	DFT-SAPT	SCS-ADC(2)	DFT-SAPT
a Using the def2-TZVP basis set. b Using the aug-cc-pVDZ basis set, with dispersion scaled to the CBS value.^42
CX2S
X = H	−1.60	−1.85	−3.38	−3.90	1.78	2.09
X = F	−2.39	−2.61	−3.47	−3.60	1.08	1.99
X = Cl	−2.67	−2.83	−4.68	−4.60	2.01	1.77
X = Br	−2.80	−3.00	−5.04	−4.96	2.24	1.96
CX2Se
X = H	−2.44	−2.43	−4.04	−4.25	1.60	1.82
X = F	−3.22	−3.20	−3.90	−3.77	0.68	0.55
X = Cl	−3.45	−3.37	−5.20	−4.76	1.75	1.39
X = Br	−3.61	−3.50	−5.68	−5.21	2.07	1.71

---

Importantly, the results of calculations obtained at the SCS-ADC(2) level show the same trends as those obtained with the DFT-SAPT method, which justifies the use of the former method for the further studies on comparison of the properties of chalcogen bonding in the ground and excited states.

The results of decomposition of the total DFT-SAPT interaction energy into the dispersion (E⁽²⁾_Disp), electrostatic (E⁽¹⁾_pol), induction (E_Ind′) and exchange (E⁽¹⁾_exch) terms are given in Table 2. For all cases the largest contribution to the complex stabilization becomes the (E⁽²⁾_Disp^CBS) term which makes 55–75% of the attraction forces. The E⁽¹⁾_pol and E_Ind′ terms correspond to about 20–30% and about 10%, respectively. All contributions, including (E⁽¹⁾_exch) terms, are significantly larger for the stacked compared to the T-shaped conformers which are given by different mutual orientations of the CX₂S(Se) and benzene subsystems reflected by the distance of their centers of mass (see Table 2).

Table 2 The DFT-SAPT/aug-cc-pVDZ stabilization energies together with all the energy components, and their relative importance listed in parentheses (in %; relative importance is defined as the ratio between the particular energy component and the sum of E⁽¹⁾_pol, E⁽²⁾_Disp^CBS and E_Ind′): E⁽¹⁾_pol = first-order electrostatic, E⁽²⁾_Disp^CBS = sum of second-order dispersion and exchange–dispersion terms scaled by a coefficient of 1.19,⁴²E_Ind′ = sum of second-order induction, exchange–induction and the dHF terms, E⁽¹⁾_exch = the first-order exchange–repulsion term, E^CBS_int* = the estimate of the complete basis set limit of the total interaction energy.⁴² All energy values are listed in kcal mol⁻¹

	R	−E^(1)pol		−E^(2)Disp^CBS		−EInd′		E ^(1)exch	−E^CBSint
a The monomer⋯monomer center of mass distance (in Å).
T-shape
C6H6⋯CX2S
X = H	3.947	0.91	(17)	4.01	(74)	0.52	(10)	3.58	1.85
X = F	4.721	1.54	(25)	4.07	(65)	0.61	(10)	3.62	2.61
X = Cl	5.107	1.73	(24)	4.65	(65)	0.76	(11)	4.32	2.83
X = Br	5.513	1.92	(25)	4.91	(64)	0.87	(11)	4.70	3.00
C6H6⋯CX2Se
X = H	3.765	1.53	(23)	4.39	(67)	0.62	(9)	4.10	2.43
X = F	4.319	2.28	(29)	4.65	(60)	0.82	(11)	4.56	3.20
X = Cl	4.710	2.47	(29)	5.16	(60)	0.97	(11)	5.23	3.37
X = Br	5.236	2.65	(29)	5.40	(59)	1.06	(12)	5.61	3.50
Stacked
C6H6⋯CX2S
X = H	3.367	3.27	(28)	6.77	(58)	1.68	(14)	7.82	3.90
X = F	3.483	2.79	(30)	5.88	(62)	0.74	(8)	5.81	3.60
X = Cl	3.609	3.64	(27)	8.54	(64)	1.17	(9)	8.75	4.60
X = Br	3.840	3.92	(27)	9.08	(63)	1.40	(10)	9.43	4.96
C6H6⋯CX2Se
X = H	3.434	4.35	(31)	7.74	(54)	2.16	(15)	9.99	4.25
X = F	3.499	3.13	(30)	6.39	(61)	0.89	(9)	6.36	3.77
X = Cl	3.507	4.14	(29)	8.91	(62)	1.43	(10)	9.72	4.76
X = Br	3.665	4.70	(29)	9.82	(61)	1.70	(10)	11.00	5.21

---

Table 3 presents the results of vertical excitation energies of the lowest excited state and emission energies obtained at the ground and excited state equilibrium geometries, respectively, together with the most important structural changes of the complexes upon excitation. The transition energies of isolated CX₂S(Se) species are given for comparison. The first excited state is characterized by transition from the lone pair orbital of S and Se, respectively, to the antibonding π* orbital of the C=S(Se) double bond. The calculated excitation energy of isolated CH₂S is 2.32 eV, in good agreement with the previously calculated and experimental adiabatic (2.00–2.09 eV)⁵² and calculated vertical energies (2.09–2.66 eV).^53,54 Only adiabatic excitation energies, in the range 1.5–1.6 eV, were reported previously for CH₂Se.⁵⁵ The substitution by halogen leads to the energy increase in the sequence X = H, Br, Cl, and F. For the majority of the cases excitation energies do not change by more than 0.1 eV upon complexation with benzene.

Table 3 The excitation energies (eV) calculated at the geometry of the ground (ΔE_exc) and excited (ΔE_em) state minima, and changes in the selected structural parameters calculated using the SCS-ADC(2) method and the def2-TZVP basis set

	Isolated				T-shape				Stacked
	ΔEexc	ΔEem	Θ	ΔrCX^b	ΔEexc	ΔEem	Θ	ΔrCX^b	ΔEexc	ΔEem	Θ	ΔrCX^b
a Dihedral angle (X-C–S(Se)-X), which defines pyramidalization of the molecule (in °). b The changes in C–S and C–Se bond distances (in Å; positive value indicates the elongation of the bond).
CX2S
X = H	2.315	1.931	0	0.11	2.303	1.932	0	0.11	2.422	1.892	4	0.13
X = F	3.803	1.691	44	0.17	3.737	1.677	44	0.17	3.730	1.578	43	0.17
X = Cl	2.691	1.605	27	0.17	2.696	1.589	27	0.17	2.755	1.464	23	0.17
X = Br	2.531	1.570	26	0.15	2.543	1.575	23	0.17	2.620	1.321	23	0.17
CX2Se
X = H	1.918	1.511	0	0.12	1.912	1.518	0	0.13	1.914	1.496	5	0.14
X = F	3.119	1.400	42	0.15	3.051	1.374	40	0.16	3.098	1.493	40	0.16
X = Cl	2.117	1.260	21	0.16	2.121	1.237	20	0.17	2.156	1.180	28	0.17
X = Br	1.986	1.210	18	0.16	2.002	1.195	19	0.17	2.110	1.116	17	0.17

---

The excited state optimization of isolated CX₂S(Se) species leads to lengthening of the C–X bond by about 0.1 and 0.2 Å for X = H and X = halogen, respectively. With the exception of CH₂S and CH₂Se, the structures of CX₂S(Se) are distorted from the planarity and pyramidalized at carbon atoms. Similar structure changes are observed also for complexes with benzene, with a slight pyramidalization of stacked benzene⋯CH₂S(Se) complexes. The excited state optimization of isolated CX₂S(Se) species leads to the lowering of transition energies by about 0.4 eV for X = H and 0.8–2.1 eV for X = halogen, respectively. The emission energies of both types of complexes have similar trends.

Similar values of transition energies and geometry parameters between ground and excited states of isolated CX₂S(Se) species and those in the complex with benzene indicate that the excitation is localized on the chalcogen molecule. This is confirmed also by inspection of molecular orbitals involved in the excitation (not shown).

Table 4 shows the results of the interaction energies calculated for the S1 equilibrium. Comparison of the ground and excited state interaction energies of T-shaped and stacked benzene⋯CX₂S(Se) complexes is also given in Table 4. In the ground state, the stacked conformers are slightly more stable, by 0.7–2.2 kcal mol⁻¹, respectively (see Table 1 and the last column of Table 4). In the excited states these differences are even smaller and do not exceed 1.5 kcal mol⁻¹. For a few complexes, in particular CH₂S, CH₂Se and CF₂Se, the reversed ordering was observed, with negligible energy differences. The results of interaction energies in the ground and excited states show that the former are larger for stacked conformers and smaller for T-shaped structures. Although the changes are very small, they reflect trends discussed in the following section.

Table 4 The interaction energies (ΔE in kcal mol⁻¹) calculated at the SCS-ADC(2) levels for the first excited state and the comparison with the interaction energies calculated for the ground state ΔΔE(S1–S0) (ΔΔE(S1–S0) = ΔE(S1) − ΔE(S0)). The differences in interaction energies between T-shaped and stacked conformers for excited electronic state ΔΔE^{“T-shape”−“Stacked”}_S1 (ΔΔE^{“T-shape”−“Stacked”}_S1 = ΔE^{“T-shape”}_S1 − ΔE^{“Stacked”}_S1) and ground electronic state ΔΔE^{“T-shape”−“Stacked”}_S0 (in parenthesis) (ΔΔE^{“T-shape”−“Stacked”}_S0 = ΔE^{“T-shape”}_S0 − ΔE^{“Stacked”}_S0) are also listed (cf. last column)

	T-shape		Stacked		ΔΔE^“T-shape”−“Stacked”S1 (ΔΔE^“T-shape“−“Stacked”S0)
	ΔE	ΔΔE(S1–S0)	ΔE	ΔΔE(S1–S0)
CX2S
X = H	−1.82	−0.23	−1.60	1.77	−0.22 (1.78)
X = F	−2.97	−0.58	−4.18	−0.71	1.21 (1.08)
X = Cl	−2.92	−0.25	−4.23	0.26	1.31 (2.01)
X = Br	−2.97	−0.02	−4.15	0.89	1.18 (2.24)
CX2Se
X = H	−2.43	−0.01	−2.37	1.65	−0.06 (1.60)
X = F	−3.74	−0.53	−2.89	1.01	−0.86 (0.68)
X = Cl	−3.67	−0.22	−4.72	0.48	1.05 (1.75)
X = Br	−3.69	−0.08	−5.00	0.69	1.31 (2.07)

---

Electrostatic potential (ESP) of monomers

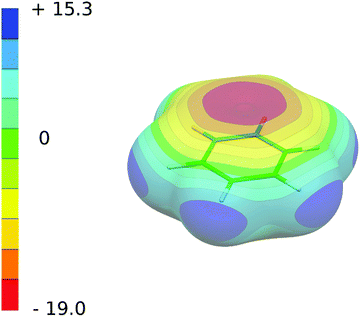
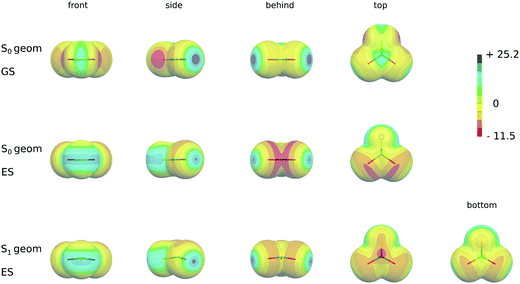
The electrostatic potential of benzene in its ground state (see Fig. 2) shows highly negative regions above and below the plane of the aromatic ring due to the π-electron system and the positive region located in the molecular plane around the hydrogen atoms. The local extrema of the ESP for CX₂S(Se) molecules in their ground state, calculated at the geometries taken from the ground state complexes with benzene, are given in Table 5 (see also Fig. 3, the first row). The ESP surface is characterized by its minimum (V_min(S,Se)) and maximum (V_max(S,Se)) localized at the S or Se atoms, respectively, and maxima at the X (V_max(X)) and carbon (V_max(C)) atoms. The minima V_min(S,Se) are located in the plane of the molecule and reflects the existence of lone pairs of S and Se atoms. Both V_max(X) and V_max(S,Se) maxima define σ-holes located in the plane of the molecule along the extension of C–X and C=S(Se) bonds, respectively. The former maximum is not, however, essential for the stability of conformers investigated in the present study. In fact, the strength of the interaction with benzene in the T-shaped structure is given mainly by the size of V_max(S,Se), while the main contribution to the stability of stacked conformers originates from V_max(C) which defines the π-hole located at carbon above and below the molecular plane (see Fig. 3, the first row).

Fig. 2 The ESP of the C₆H₆ molecule in the ground electronic state (perspective view). The ESP color scale in kcal mol⁻¹. The 0.001 e Bohr⁻³ isodensity is depicted. Shown structure is cut from the S0 optimized geometry of the C₆H₆⋯CBr₂Se T-shaped complex.

Table 5 The local extrema (V_min – minimum and V_max – maximum) of the ESP at the 0.001 a.u. isodensity surface for methanethial (CH₂S) and methaneselone (CH₂Se) and all their halogen derivatives in their electronic ground and excited states calculated at the ground state geometry. Local extrema are shown for S(Se), C and X (X = halogen) atom sites. Values are listed in kcal mol⁻¹

	Ground state				Excited state
	V min	V max			V min	V max
	(S,Se)	(S,Se)	(X)	(C)	(S,Se)	(S,Se)	(X)	(C)
T-shape
C6H6⋯CX2S
X = H	−21.54	−1.05	26.57	—	−11.03	7.07	20.19	−14.53
X = F	−10.93	15.51	−0.98	35.48	−0.57	24.34	—	9.38
X = Cl	−12.47	12.60	20.00	18.86	0.06	22.46	13.5	0.69
X = Br	−11.54	13.10	25.24	15.72	−0.33	21.44	21.6	−0.84
C6H6⋯CX2Se
CH2Se	−20.76	5.00	27.06	—	−0.74	12.09	19.03	−16.08
X = F	−12.45	21.82	0.44	34.92	−1.99	30.4	—	6.41
X = Cl	−14.25	17.57	21.16	17.82	−0.65	27.95	12.36	−1.99
X = Br	−13.40	18.01	26.24	14.25	—	27.52	19.87	−2.82
Stacked
C6H6⋯CX2S
X = H	−21.47	−1.00	26.53	—	−10.99	6.91	20.19	−14.47
X = F	−11.13	15.23	−0.80	35.69	−0.74	24.09	—	9.51
X = Cl	−12.76	12.18	20.21	19.02	−0.14	22.19	13.62	0.73
X = Br	−11.96	12.73	25.59	15.89	−0.48	21.38	21.63	−0.65
C6H6⋯CX2Se
X = H	−20.74	4.90	27.04	—	—	11.96	19.14	−16.10
X = F	−12.43	21.66	0.39	35.35	−2.01	30.17	—	6.50
X = Cl	−14.31	17.33	21.19	17.90	−0.72	27.68	12.43	−1.87
X = Br	−13.46	17.80	26.27	14.33	—	27.26	19.92	−2.68

---

Fig. 3 The ESPs of the CBr₂S molecule: the first row: the ESP of the ground (S0) state for the S0 structure. The second row: the ESP of the excited (S1) state for the S0 structure. The third row: the ESP of the excited (S1) state for the S1 structure. Depicted structures were taken from the respective S0 and S1 optimized geometry of the C₆H₆⋯CBr₂S T-shaped complex. The ESP color scale in kcal mol⁻¹. The 0.001 a.u. isodensity is depicted. The front, side, behind, top and bottom (in the case of the pyramidal S1 structure) views are presented.

The values of V_max(S,Se) and V_min(S,Se) reflect the inductive effects of halogens. In particular V_max(S,Se) has a slightly negative or slightly positive value in the case of CH₂S and CH₂Se complexes, respectively, and its magnitude greatly increases by substitution with halogen atoms. In line with the observation of a smaller electron density due to the halogen inductive effect the highly negative value of V_min(S,Se) with X = H reduces to half when X is the halogen atom. The trends discussed above are consistent with the observation reported previously in several studies which report on the tunability of the halogen bond.^56–59 The size of V_max(C) is even more sensitive to the electronegativity and inductive effect of the halogen atoms. In particular, the electronegativity of F, Cl, and Br atoms decreases by 1 (F versus Cl) and 0.2 (Cl versus Br), and the size of the π-hole decreases by almost the same ratios. Note that ESP surfaces of CH₂S and CH₂Se do not show any existence of the π-hole. In general, the σ-holes on CX₂Se are larger compared to those on CX₂S, in line with a larger polarizability and smaller electronegativity of the former species.⁶⁰ The sizes of the π-holes show opposite trends with, however, much smaller differences.

Table 5 also shows the results of the ESP calculations in the excited state at the ground state geometry, which correspond to the changes upon the vertical excitation (see also Fig. 3, second row). During the excitation the electrons are transferred from the lone-pair orbital into the antibonding π* orbital of the C–S(Se) double bonds which results in a substantial redistribution of the electron density around the molecule. In particular, the absolute value of the minimum (V_min(S,Se)) originally located at the position of the lone pairs significantly decreases and moves from the molecular plane towards the p-type orbital which is a part of the π-orbital system. The area of the ESP with a positive value greatly enlarges around the chalcogen atoms and forms a belt in the plane of the molecule (see Fig. 3, second row). Additionally the value of V_max(S,Se) significantly increases upon excitations (see Table 5 and Fig. 3). Even larger changes appear at carbon atoms. The transfer of the electron into the antibonding π* orbital results in the negative ESP surface of CH₂S and CH₂Se in this region and depletion of the positive region of the π-hole of CX₂S(Se) with X = F, Cl (see Fig. 3, the second row). Its size depends on the halogen atom. The more electronegative F atom accepts the electron density leaving still the π-hole on the ESP surface, although much smaller than in the ground state. This almost diminishes when X = Cl and becomes even slightly negative with Br atoms. Note that the magnitude of V_max(X) does not significantly change upon excitation (see Table 5 and Fig. 3, the second row).

Table 6 shows the results of the excited state ESP calculated at the geometry of S1 minima (see also Fig. 3, the third row). For X = F, Cl and Br the V_min(Se, S) values are slightly larger and V_max(S,Se) values are slightly smaller, respectively, than the excited state ESP values obtained at the ground state geometry. Similarly, the size of the σ-hole (V_max(X)) does not significantly change for X = Cl, Br. As in the case of the vertical excitation no maximum appears in the case of X = F. In addition, due to its large inductive effect a new and relatively large minimum appears at the F atom. As a consequence of the structure changes in the S1 minimum, in particular the pyramidalization at the C atom, the character of the ESP surface at the carbon atom significantly changes. In particular, the sizes of the π-hole above and below the molecular plane differ with smaller values of the former and V_max(C) is slightly shifted. In addition, a new minimum appears in this region (see Fig. 3, the third row).

Table 6 The local extrema (V_min – minimum and V_max – maximum) of the ESP at the 0.001 a.u. isodensity surface for methanethial (CH₂S) and methaneselone (CH₂Se) and all their halogen derivatives in their excited electronic state calculated at the excited electronic state geometry. Local extrema are shown for S(Se), C and X (X = halogen) atom sites. Values are listed in kcal mol⁻¹

	V min	V max	V max	V max	V max	V min
	(S,Se)	(S,Se)	(X)	(C)up^a	(C)down^a	Cup^a
a See Fig. 3, third row.
T-shape
C6H6⋯CX2S
X = H	—	8.57	21.40	−15.73	−15.69	—
X = F	−4.78; −0.84	21.72	—; −10.62	12.24	15.74	−7.80
X = Cl	−2.61	20.57	16.08	2.47	6.34	−8.57
X = Br	−2.04	20.45	22.85	1.40	4.44	−9.26
C6H6⋯CX2Se
X = H	—	14.25	20.39	−17.47	−17.50	—
X = F	−5.57; −2.21	25.63	—; −10.52	10.55	14.28	−8.98
X = Cl	−3.62	26.5	16.19	0.69	3.89	−9.55
X = Br	−2.97	26.73	22.69	−0.48	1.63	−10.19
Stacked
C6H6⋯CX2S
X = H	—	8.66	21.48	−17.57	−13.78	—
X = F	−4.73; −0.66	21.43	—; −11.20	13.28	14.63	−7.68
X = Cl	−2.17	20.2	15.03	3.36	6.88	−9.59
X = Br	−1.18	20.53	21.59	1.79	5.05	−10.38
C6H6⋯CX2Se
X = H	—	14.47	20.35	−18.53	−16.56	—
X = F	−5.77; −2.46	25.62	—; −10.97	10.49	14.96	−9.05
X = Cl	−2.95	25.83	15.01	1.34	4.88	−10.79
X = Br	−1.88	26.2	21.41	0.12	3.05	−11.71

---

As discussed above the relative stabilities of T-shaped and stacked conformers in the ground states change upon excitation into the S1 state. Although the changes are very small, they follow the trends, which can be explained by the changes in the character of ESP surfaces upon excitation. In particular, stronger binding of all T-shaped complexes in their excited states compared to ground state reflects the changes in the ESP at the chalcogen atom and correlates with larger (in terms of the size and absolute value) σ-holes in the excited states. A lower stability of the most stacked complexes in the excited state is consistent with ESP changes at carbon atoms. Relatively large negative ESP values in the excited states appear for CH2S and CH2Se. For halogen-substituted species a significant depletion of π-holes together with sizable ESP minima were found in this region. As a result, the increased positive region of the ESP at chalcogen atoms together with its V_max(S) and V_max(Se) values and the decreased size of the π-hole at C atoms interacting with the negative ESP surface of benzene result in the increased stability of the T-shaped and decreased stability of stacked complexes, respectively, in the excited states.

Conclusions

The character of the ESP surface of CH₂S and CH₂Se and their fluoro-, chloro-, bromo- derivatives significantly changes upon excitation from the chalcogen lone pairs into the antibonding π* orbital. The magnitude of the σ-hole at the chalcogen atom site increases and the π-hole located at the carbon site reduces, respectively, upon excitation. These changes affect the strength of binding in the complexes. The stability of the T-shaped conformers is determined mainly by the character of the ESP surface at the chalcogen atom. Due to its increased size upon excitation the interaction of CX₂S and CX₂Se with the negative ESP of benzene is stronger in the excited state than in the ground state. In the stacked conformers, the benzene molecule interacts with the π-hole at the carbon atom. Its depletion upon excitation is responsible for a larger stability of the complexes in the ground state compared to the excited state. Although the observed changes in the ESP character are relatively large, the resulting changes in binding are very small. This situation very likely reflects a relative importance of other contributions to the total stabilization energies. Nevertheless, the binding energies follow the trends of non-covalent chalcogen interactions occurring upon the changes in the electronic state, which can be rationalized by the different redistribution of electron density of interacting monomers.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was part of the Research Project RVO: 61388963 of the Institute of Organic Chemistry and Biochemistry, Academy of Sciences of the Czech Republic. Authors acknowledge the support from the Czech Science Foundation (project no. GA16-16959S).

References

1. O. Bolton, K. Lee, H.-J. Kim, K. Y. Lin and J. Kim, Nat. Chem., 2011, 3, 205–210.
2. A. V. Jentzsch, D. Emery, J. Mareda, S. K. Nayak, P. Metrangolo, G. Resnati, N. Sakai and S. Matile, Nat. Commun., 2012, 3, 905.
3. A. Priimagi, G. Cavallo, A. Forni, M. Gorynsztejn–Leben, M. Kaivola, P. Metrangolo, R. Milani, A. Shishido, T. Pilati, G. Resnati and G. Terraneo, Adv. Funct. Mater., 2012, 22, 2572–2579.
4. A. Priimagi, G. Cavallo, P. Metrangolo and G. Resnati, Acc. Chem. Res., 2013, 46, 2686–2695.
5. J. Fanfrlík, A. Přáda, Z. Padělková, A. Pecina, J. Macháček, M. Lepšík, J. Holub, A. Růžička, D. Hnyk and P. Hobza, Angew. Chem., Int. Ed., 2014, 53, 10139–10142.
6. D. B. Werz, R. Gleiter and F. Rominger, J. Am. Chem. Soc., 2002, 124, 10638–10639.
7. M. Iwaoka, S. Takemoto and S. Tomoda, J. Am. Chem. Soc., 2002, 124, 10613–10620.
8. M. Iwaoka, S. Takemoto, M. Okada and S. Tomoda, Chem. Lett., 2001, 132–133.
9. F. T. Burling and B. M. Goldstein, J. Am. Chem. Soc., 1992, 114, 2313–2320.
10. Y. Nagao, T. Hirata, S. Goto, S. Sano, A. Kakehi, K. Iizuka and M. Shiro, J. Am. Chem. Soc., 1998, 120, 3104–3110.
11. D. Yan, A. Delori, G. O. Lloyd, T. Friščić, G. M. Day, W. Jones, J. Lu, M. Wei, D. G. Evans and X. Duan, Angew. Chem., Int. Ed., 2011, 50, 12483–12486.
12. Y. Sonoda, M. Goto, S. Tsuzuki and N. Tamaoki, J. Phys. Chem. A, 2007, 111, 13441–13451.
13. D. Yan, H. Yang, Q. Meng, H. Lin and M. Wei, Adv. Funct. Mater., 2014, 24, 587–594.
14. W. Zhu, R. Zheng, Y. Zhen, Z. Yu, H. Dong, H. Fu, Q. Shi and W. Hu, J. Am. Chem. Soc., 2015, 137, 11038–11046.
15. T. Clark, M. Hennemann, J. S. Murray and P. Politzer, J. Mol. Model., 2007, 13, 291–296.
16. P. Politzer, J. S. Murray and T. Clark, Phys. Chem. Chem. Phys., 2010, 12, 7748–7757.
17. R. F. W. Bader, M. T. Carroll, J. R. Cheeseman and C. Chang, J. Am. Chem. Soc., 1987, 109, 7968–7979.
18. R. F. Stewart, Chem. Phys. Lett., 1979, 65, 335–342.
19. T. S. Koritsanszky and P. Coppens, Chem. Rev., 2001, 101, 1583–1627.
20. M. Kolář, J. Hostaš and P. Hobza, Phys. Chem. Chem. Phys., 2014, 16, 9987–9996.
21. P. Politzer, J. S. Murray and T. Clark, J. Mol. Model., 2015, 21, 52.
22. J. S. Murray, P. Lane, T. Clark, K. E. Riley and P. Politzer, J. Mol. Model., 2012, 18, 541–548.
23. A. F. Cozzolino, P. J. W. Elder and I. Vargas-Baca, Coord. Chem. Rev., 2011, 255, 1426–1438.
24. A. Kremer, A. Fermi, N. Biot, J. Wouters and D. Bonifazi, Chem. – Eur. J., 2016, 22, 5665–5675.
25. P. C. Ho, P. Szydlowski, J. Sinclair, P. J. W. Elder, J. Kübel, C. Gendy, L. M. Lee, H. Jenkins, J. F. Britten, D. R. Morim and I. Vargas-Baca, Nat. Commun., 2016, 7, 11299–11309.
26. H.-T. Huynh, O. Jeannin and M. Fourmigué, Chem. Commun., 2017, 53, 8467–8469.
27. A. Bauzá, D. Quiñonero, P. M. Deyà and A. Frontera, CrystEngComm, 2013, 15, 3137–3144.
28. C. R. Groom, I. J. Bruno, M. P. Lightfoot and S. C. Ward, Acta Crystallogr., Sect. B: Struct. Sci., Cryst. Eng. Mater., 2016, 72, 171–179.
29. K. S. C. Reid, P. F. Lindley and J. M. Thornton, FEBS Lett., 1985, 190, 209–213.
30. I. J. Bruno, J. C. Cole, P. R. Edgington, M. Kessler, C. F. Macrae, P. McCabe, J. Pearson and R. Taylor, Acta Crystallogr., Sect. B: Struct. Sci., 2002, 58, 389–397.
31. K. T. Mahmudov, M. N. Kopylovich, M. F. C. Guedes da Silva and A. J. L. Pombeiro, Dalton Trans., 2017, 46, 10121–10138.
32. V. Georgakilas, M. Otyepka, A. B. Bourlinos, V. Chandra, N. Kim, K. C. Kemp, P. Hobza, R. Zboril and K. S. Kim, Chem. Rev., 2012, 112, 6156–6214.
33. P. Politzer, J. S. Murray and T. Clark, Phys. Chem. Chem. Phys., 2013, 15, 11178–11189.
34. J. Schirmer, Phys. Rev. A: At., Mol., Opt. Phys., 1982, 26, 2395–2416.
35. A. B. Trofimov and J. Schirmer, J. Phys. B: At., Mol. Opt. Phys., 1995, 28, 2299.
36. F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305.
37. S. F. Boys and F. Bernardi, Mol. Phys., 1970, 19, 553–566.
38. B. Jeziorski, R. Moszynski and K. Szalewicz, Chem. Rev., 1994, 94, 1887–1930.
39. A. Heßelmann, G. Jansen and M. Schütz, J. Chem. Phys., 2005, 122, 014103.
40. D. E. Woon and T. H. Dunning Jr, J. Chem. Phys., 1993, 98, 1358–1371.
41. A. K. Wilson, D. E. Woon, K. A. Peterson and T. H. Dunning, J. Chem. Phys., 1999, 110, 7667–7676.
42. J. Řezáč and P. Hobza, J. Chem. Theory Comput., 2011, 7, 685–689.
43. J. B. Foresman, M. Head-Gordon, J. A. Pople and M. J. Frisch, J. Phys. Chem., 1992, 96, 135–149.
44. M. J. Frisch, G. W. Trucks, J. R. Cheeseman, G. Scalmani, M. Caricato, H. P. Hratchian, X. Li, V. Barone, J. Bloino, G. Zheng, T. Vreven, J. A. Montgomery, G. A. Petersson, G. E. Scuseria, H. B. Schlegel, H. Nakatsuji, A. F. Izmaylov, R. L. Martin, J. L. Sonnenberg, J. E. Peralta, J. J. Heyd, E. Brothers, F. Ogliaro, M. Bearpark, M. A. Robb, B. Mennucci, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, A. Rendell, R. Gomperts, V. G. Zakrzewski, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao and H. Nakai, Gaussian 09, 2009.
45. T. Lu and F. Chen, J. Comput. Chem., 2012, 33, 580–592.
46. T. Lu and F. Chen, J. Mol. Graphics Modell., 2012, 38, 314–323.
47. W. DeLano, The PyMOL (TM) Molecular Graphics System, Schrodinger, LLC.
48. S. Portmann and P. Fluekiger, Molekel 4.3, 2002.
49. TURBOMOLE V6.2 2010, a development of University of Karlsruhe and Forschungszentrum Karlsruhe GmbH, 1989.
50. H.-J. Werner, P. J. Knowles, G. Knizia, F. R. Manby, M. Schütz, P. Celani, W. Györffy, D. Kats, T. Korona, R. Lindh, A. Mitrushenkov, G. Rauhut, K. R. Shamasundar, T. B. Adler, R. D. Amos, A. Bernhardsson, A. Berning, D. L. Cooper, M. J. O. Deegan, A. J. Dobbyn, F. Eckert, E. Goll, C. Hampel, A. Hesselmann, G. Hetzer, T. Hrenar, G. Jansen, C. Köppl, Y. Liu, A. W. Lloyd, R. A. Mata, A. J. May, S. J. McNicholas, W. Meyer, M. E. Mura, A. Nicklass, D. P. O’Neill, P. Palmieri, D. Peng, K. Pflüger, R. Pitzer, M. Reiher, T. Shiozaki, H. Stoll, A. J. Stone, R. Tarroni, T. Thorsteinsson and M. Wang, MOLPRO, version 2015.1, a package of ab initio programs, Molpro, 2015.
51. M. Saberinasab, S. Salehzadeh, Y. Maghsoud and M. Bayat, Comput. Theor. Chem., 2016, 1078, 9–15.
52. K. A. Nguyen, P. N. Day and R. Pachter, Int. J. Quantum Chem., 2010, 110, 2247–2255.
53. C. Limbachiya, A. Chaudhari, H. Desai and M. Vinodkumar, RSC Adv., 2015, 5, 103964–103976.
54. Y.-F. Wang and S. X. Tian, Phys. Rev. A: At., Mol., Opt. Phys., 2011, 84, 022709.
55. D. C. Moule, L. Chantranupong, R. H. Judge and D. J. Clouthier, Can. J. Chem., 1993, 71, 1706–1712.
56. K. E. Riley, J. S. Murray, J. Fanfrlík, J. Rezáč, R. J. Solá, M. C. Concha, F. M. Ramos and P. Politzer, J. Mol. Model., 2011, 17, 3309–3318.
57. L. A. Hardegger, B. Kuhn, B. Spinnler, L. Anselm, R. Ecabert, M. Stihle, B. Gsell, R. Thoma, J. Diez, J. Benz, J.-M. Plancher, G. Hartmann, Y. Isshiki, K. Morikami, N. Shimma, W. Haap, D. W. Banner and F. Diederich, ChemMedChem, 2011, 6, 2048–2054.
58. L. A. Hardegger, B. Kuhn, B. Spinnler, L. Anselm, R. Ecabert, M. Stihle, B. Gsell, R. Thoma, J. Diez, J. Benz, J.-M. Plancher, G. Hartmann, D. W. Banner, W. Haap and F. Diederich, Angew. Chem., Int. Ed., 2011, 50, 314–318.
59. R. Wilcken, X. Liu, M. O. Zimmermann, T. J. Rutherford, A. R. Fersht, A. C. Joerger and F. M. Boeckler, J. Am. Chem. Soc., 2012, 134, 6810–6818.
60. J. S. Murray, M. C. Concha, P. Lane, P. Hobza and P. Politzer, J. Mol. Model., 2008, 14, 699–704.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c7cp05537d

---