Ultrathin gold film modified optical properties of excitons in monolayer MoS2

Abstract

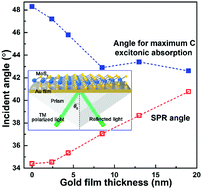
Metal nanostructure plays an important role in tailoring the performance of various two-dimensional semiconductors. Herein, we theoretically study the optical properties of A, B and C excitons in monolayer MoS₂ coated on ultrathin gold films less than 20 nm in thickness. We show that resonances of these three excitons occur at ∼660, ∼613 and ∼426 nm, respectively and each exciton maximizes absorption intensity at total reflection. However, because of the optical scattering effect induced by the ultrathin gold film, the maximum absorption of each exciton appears at the incident angle θ_m that is larger than its corresponding surface plasmon resonance angle θ_SPR. It is possible that due to the gradual approach between θ_m and θ_SPR, the maximum absorption intensity of the exciton gradually increases with thickening of the gold film. For external reflection, the C exciton maximizes absorption intensity around its corresponding quasi-Brewster's angle, whereas the incident angle, at which the A or B exciton gives the maximum absorption, gradually deviates from its corresponding quasi-Brewster's angle as the gold film thickness decreases. This discrepancy is explained by the dependencies of extinction coefficients of hybrid films on the excitonic resonance wavelength and gold film thickness.