Open Access Article
Open Access ArticleSolvation of apolar compounds in protic ionic liquids: the non-synergistic effect of electrostatic interactions and hydrogen bonds†
I. A.
Sedov
 *,
T. I.
Magsumov
,
T. M.
Salikov
and
B. N.
Solomonov
*,
T. I.
Magsumov
,
T. M.
Salikov
and
B. N.
Solomonov
Chemical Institute, Kazan Federal University, Kremlevskaya 18, 420008, Kazan, Russia. E-mail: igor_sedov@inbox.ru
First published on 24th August 2017
Abstract
The solvation properties of protic ionic liquids such as alkylammonium salts are still virtually uncharacterized. Both electrostatic interactions between charged particles and hydrogen bond networks in a solvent are known to hinder the solubility of apolar species. Protic ionic liquids can be a priori expected to dissolve hydrocarbons worse than aprotic ionic liquids which do not form hydrogen bonds between the ions. We measured the limiting activity coefficients of several alkanes and alkylbenzenes in propylammonium and butylammonium nitrates at 298 K. Surprisingly, we observed the tendency of higher solubility than for the same compounds in aprotic ionic liquids with a similar molar volume. The calculations of the excess Gibbs free energies using test particle insertions into the snapshots of molecular dynamics trajectories reproduced lower values in protic rather than in aprotic ionic liquids for both methane molecules and hard sphere solutes. This can be explained by the favorable solvation of apolar species in the apolar domain of nanostructured PILs. For the first time, we point out at the essential difference between the solvation properties of two types of ionic liquids and prove that it arises from the cavity formation term.
Introduction
Protic ionic liquids (PILs) are a huge group of ionic liquids that can be obtained in the reaction of a Brønsted acid with a Brønsted base and have both proton-donor and proton-acceptor centers in their molecules.1 Most of the synthesized PILs are salts of nitrogenous bases. Historically, ethylammonium nitrate was the first room temperature ionic liquid to be synthesized.2 However, the thermodynamic properties of PILs are characterized to a lesser extent in comparison with aprotic ionic liquids. In particular, only a few studies3–7 were dedicated to the solvation properties of PILs despite their prospective use as industrial solvents. This is explained3 by the experimental difficulties in measuring the activity coefficients, excess enthalpies and other infinite-dilution thermochemical properties of solutions in these solvents.The presence of oppositely charged ions in aprotic ionic liquids leads to a significant drop in the solubility of apolar species, which decreases with increasing concentration of ion pairs per unit volume of a liquid.8 The same is true for protic non-ionic solvents, where the solubility decreases with increasing concentration of intermolecular hydrogen bonds.9 In addition, aprotic ionic liquids (AILs) are known to have very small vapor pressures and huge enthalpies of vaporization due to strong interactions between the ions. Hydrogen bonds in protic molecular solvents also decrease their volatility and increase the energy cost of vaporization, at least relative to aprotic solvents, which are often demonstrated using a comparison of water (Tb = 373.15 K, ΔvapH = 44 kJ mol−1 at 298 K) with hydrogen sulfide (Tb = 212.9 K, ΔvapH = 18.6 kJ mol−1 at 298 K) or various protic and aprotic organic compounds. At first glance, the combination of the two factors, Coulombic interactions and hydrogen bonds, should lead to an even more pronounced decrease in the solubility and volatility of the apolar species. Unfortunately, the solubility-related properties, such as limiting activity coefficients in PILs, are too scarce in the literature to infer any conclusions. At the same time, recent studies on the vaporization of PILs10,11 have shown that they have smaller enthalpies of vaporization than AILs with the same anions and the cation with a similar size.
The structure of several alkylammonium PILs including nitrates and other salts of ethylammonium, propylammonium, and butylammonium was studied using small-angle neutron scattering,12 large-angle X-ray scattering,13 neutron diffraction,14,15 and molecular dynamics simulations.13,16 It has been proven that these liquids are structurally inhomogeneous and consist of polar and apolar domains. Charged and uncharged groups tend to segregate due to favorable solvophobic interactions between alkyl chains resulting in sponge-like nanostructures.14 Such a segregation can have a strong impact on various properties of PILs.
In the present study, we experimentally determine the limiting activity coefficients γ∞ of several apolar compounds in two PILs, propylammonium and butylammonium nitrates at 298 K, and compare them with the corresponding values for the same solutes in various AILs. The limiting activity coefficients are related to the standard Gibbs free energy change ΔsolvG° upon solvation of a solute from the gas phase into a solvent using the equation
ΔsolvG° = RT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(γ∞psat/p°), ln(γ∞psat/p°), | (1) |
Experimental
Chemicals
All the chemicals used in experiments were purchased from commercial suppliers. No additional purification of compounds was done. The absence of significant amounts of impurities in organic compounds was confirmed by gas chromatography.Synthesis of protic ionic liquids
Alkylamine and nitric acid were diluted with distilled water and cooled down to −20 °C. Nitric acid was added dropwise to aqueous alkylamine under constant stirring and cooling in an ice-salt bath. A small excess of alkylamine was used. After the addition was finished, water and alkylamine were removed in a rotary evaporator under vacuum at 50–60 °C. The absence of significant amounts of water (<0.2 wt%) was confirmed using Karl Fischer titration and FTIR spectra (Fig. 1). Propylammonium nitrate (PAN) was obtained as a pale yellow liquid with ρ = 1.157 g cm−3, nD = 1.4548 at 298.15 K, and mp 276 K (measured using DSC at 10 K min−1). 1H NMR (D2O, 400 MHz, ppm): δ 2.88 (t, 2H, J = 7.5 Hz), 1.59 (m, 2H), and 0.88 (t, 3H, J = 7.4 Hz). Butylammonium nitrate (BAN) is a white crystal melting at 303 K into a yellow liquid, which is prone to supercooling. At 298.15 K, this liquid has ρ = 1.112 g cm−3, and nD = 1.4545. Slow cooling leads to the formation of another crystalline modification of BAN melting at 283 K. 1H NMR (D2O, 400 MHz, ppm): δ 2.99 (t, 2H, J = 7.6 Hz), 1.62 (m, 2H), 1.36 (m, 2H), and 0.90 (t, 3H, J = 7.4 Hz). See the ESI† for the comparison of the measured physical properties with literature data. Both ionic liquids were stored in sealed vials in a desiccator over phosphorus pentoxide to prevent the absorption of water from air.A headspace analysis technique for the measurement of limiting activity coefficients
The limiting activity coefficients of hydrocarbons in PILs were determined by means of gas chromatographic analysis of the headspace over dilute solutions. The experimental setup was the same as described in previous publications.17,18 2–10 μL of the solute was put into a vial containing 5 mL of the solvent. The vials were sealed, shaken and thermostatted at 298.15 K for several hours. Vapor samples were taken from the headspace using an autosampler and transferred into a gas chromatograph. The areas of the chromatographic peaks of each substance are proportional to the vapor pressure of this substance. Thus, the activity coefficients can be determined from the ratio of the chromatographic peak areas in experiments with a pure substance and its solution. The obtained values of γ∞ were averaged over 6 repetitions for each system at different concentrations of a solute. They showed no significant concentration dependence proving that infinite dilution is reached. The obtained results are given in Table 1. The values of ΔsolvG° were calculated by using eqn (1) and they correspond to the molar-fraction based standard state for solutions at a standard pressure of 1 bar.| Solute | Solvent | γ ∞ | u (γ∞) | ΔsolvG°/kJ mol−1 |
|---|---|---|---|---|
| a Standard uncertainty for temperature u(T) = 0.2 K. The experimental pressure inside vials p = 2.38 bar and u(p) = 0.01 bar. | ||||
| n-Hexane | PAN | 117 | 8 | 7.82 |
| n-Heptane | PAN | 247 | 11 | 6.73 |
| n-Octane | PAN | 445 | 17 | 5.26 |
| n-Nonane | PAN | 910 | 29 | 4.18 |
| Benzene | PAN | 8.37 | 0.32 | 0.14 |
| Toluene | PAN | 13.7 | 0.4 | −1.63 |
| Ethylbenzene | PAN | 22.0 | 0.6 | −3.14 |
| Butylbenzene | PAN | 63.7 | 2.2 | −5.97 |
| n-Hexane | BAN | 38.8 | 1.5 | 5.09 |
| n-Heptane | BAN | 62.0 | 2.3 | 3.31 |
| n-Octane | BAN | 86.9 | 3.1 | 1.22 |
| n-Nonane | BAN | 154 | 10 | −0.22 |
| Benzene | BAN | 4.62 | 0.12 | −1.33 |
| Toluene | BAN | 7.62 | 0.22 | −3.08 |
| Ethylbenzene | BAN | 9.94 | 0.24 | −5.11 |
| Butylbenzene | BAN | 19.4 | 0.3 | −8.91 |
Discussion
Comparison with the literature data for solvation in EAN
In the literature, there are few experimental data on the solvation properties of ethylammonium nitrate (EAN) which can be compared with our results for PAN and BAN. Evans et al. reported4 the Gibbs free energies of solvation of krypton, methane, ethane, and n-butane in EAN. In a more recent work,3 the activity coefficients of C13–C15n-alkanes, C8–C11 alkylbenzenes, and several polar solutes in EAN were measured. The results of these works and our data are plotted against the number of carbon atoms in n-alkane as shown in Fig. 2. The values of the saturated vapor pressure of C13–C15n-alkanes which are necessary to convert the activity coefficients into the Gibbs free energies of solvation were taken from ref. 19. Despite a large gap in the plot for alkanes between C4 and C13 that were not studied in EAN, the trend in decreasing the Gibbs free energies of solvation for the same solute upon increasing the number of carbons in a PIL molecule can be noticed. Similarly, the Gibbs free energies of solvation of alkylbenzenes decrease in a sequence EAN > PAN > BAN.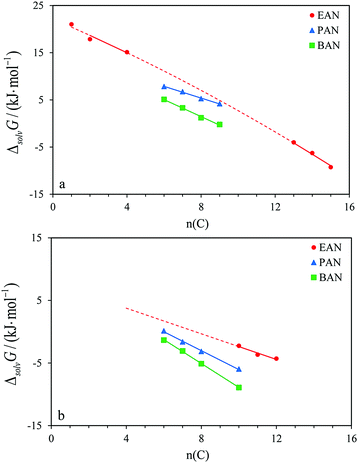 | ||
| Fig. 2 Standard molar Gibbs free energies of solvation for (a) n-alkanes, and (b) n-alkylbenzenes in EAN,3,4 PAN, and BAN against the number of carbons in a solute molecule. | ||
Selectivity for alkane/arene separation
Ionic liquids are considered as prospective solvents for use in separation processes, particularly for the separation of aliphatic and aromatic hydrocarbons by extractive distillation. A commonly used measure of separation selectivity is the ratio of the limiting activity coefficients of two separated species S = γ∞1/γ∞2. Our results indicate that the selectivity of considered PILs for alkane/alkylbenzene separation problem is lower than those of many AILs20 and of some conventional molecular solvents used in separation processes such as sulfolane and N-methylpyrrolidone, which is in agreement with the previous observation for EAN.3 For the n-hexane/benzene system, S = 14 in the case of PAN and 8.5 in the case of BAN, for the n-heptane/toluene system S = 17 and 8.2, and for the n-octane/ethylbenzene system S = 20 and 8.7, respectively.Comparison of the solvation properties of protic and aprotic ionic liquids
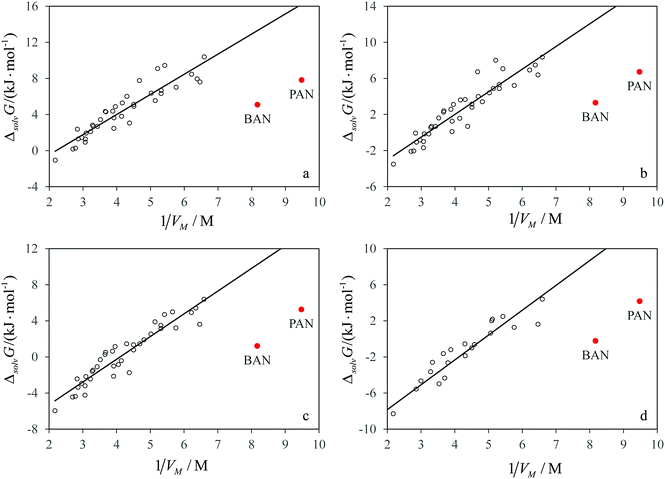
Comparison of the solvation properties of the studied solvents with AILs should be made with regard to a large difference in the values of the limiting activity coefficients for the same solute in different AILs. It would be ideal to compare the values obtained in n-butylammonium nitrate and its aprotic isomer, tetramethylammonium nitrate, but the latter melts as high as at 683 K.21 Many other tetraalkylammonium nitrates also melt well above room temperature. In order to compare PAN and BAN with the ionic liquids having a non-ammonium cation and/or an anion different from nitrate, one should know how the solvation properties of AILs depend on the structure of ions constituting them.In our recent work, we have shown that for many AILs consisting of different cations and anions, there is a good linear correlation between the Gibbs free energy of solvation of n-alkane and the inverse molar volume of the ionic liquid, which has a physical sense of the concentration of ion pairs per unit volume of the AIL. In Fig. 3a–d, the data for n-alkanes from Table 1 are combined with the Gibbs free energies of solvation for the same solutes in various AILs.8 It is clear that for all the solutes the data points corresponding to PILs lie below the correlation line of ΔsolvG° with 1/Vm for AILs, which means an increase in solubility of hydrocarbons in PILs in comparison with AILs of the same molecular size.
The linear growth of the Gibbs free energy of solvation of hydrocarbons in AILs with the concentration of ion pairs is linked with the existence of the solvophobic effects caused by the electrostatic interactions between the ions.8 These effects cause the self-assembly of amphiphilic molecules into micelles, vesicles and other supramolecular structures, which was observed in many AILs.22 In protic molecular solvents, solvophobic effects cause a similar trend in decreasing solubility and increasing Gibbs free energy of solvation of apolar species upon increasing the concentration of hydrogen bonds per unit volume of a solvent. Protic ionic liquids, which combine the ionic structure with intermolecular hydrogen bonds, could be expected to reduce the solubility of hydrocarbons more than AILs leading to positive deviations of the data points for solvation in PILs from the correlations shown in Fig. 3a–d. In fact, we observe an opposite tendency.
Cavity formation contribution
In order to understand the origin of the increased solubility of hydrocarbons in PILs, we tried to evaluate and compare the Gibbs free energy of formation of a cavity in various PILs and AILs. The cavity term contributes to the thermodynamic functions of solvation of any solute in any solvent. It is known to be responsible for the existence of the hydrophobic effect in water.23,24 The cavity formed upon solvation is assumed to have the size sufficient to accommodate a solute molecule, so that the total magnitude of the Gibbs free energy of solvation can be represented as the sum of the cavity formation contribution ΔcavG and the energy of interactions ΔintG between the solute and the solvent upon transferring of the solute into this cavity:| ΔsolvG° = ΔcavG + ΔintG | (2) |
It is reasonable to expect that ΔcavG is proportional to the volume of a cavity even for the cavities with a complicated non-spherical shape.26 Thus, the comparison of the Gibbs free energies of formation of a cavity with the same radius in different solvents allows the arrangement of these solvents by the energy cost of cavity formation for any molecule of not too large size. Moreover, Widom's method allows calculating the Gibbs free energies of solvation of monoatomic molecules, such as noble gases or methane in a united-atom approach, and evaluating the contribution from solute–solvent interactions ΔintG in addition to the cavity term.
We performed the calculations for three protic ionic liquids: EAN, PAN, and BAN, and two aprotic ionic liquids: tetramethylammonium nitrate (TMAN) and trimethylbutylammonium nitrate (TMBAN) at 298 K, which are in fact supercooled liquids that do not crystallize within the simulation time.
Molecular dynamics simulations were conducted using the Gromacs 5.1 software. Two variations of the OPLS force field with different interaction parameters were tried. The first variation was based on the OPLS-AA parameters of nonbonded interactions and atomic charges used by Umebayashi et al.16 for the simulations of EAN, PAN, and BAN. The standard OPLS-AA parameters of bond stretching, bending and torsion were applied to the cations. For nitrate anions, these parameters were taken from the work27 as well as the values of atomic charges in trimethylbutylammonium and tetramethylammonium cations. However, attempts to model TMAN using this set of parameters always resulted in its fast crystallization, therefore it was not studied.
For the second set of models, we used the OPLS-UA force field. We used the interaction parameters and atomic charges for methylammonium and tetramethylammonium cations reported by Jorgensen28 and the standard bond stretching and bending parameters. Instead of zero values of van der Waals interaction parameters σ and ε for ammonium hydrogens in PILs, we used the same values as in the above-described OPLS-AA model. The interaction parameters for the nitrate anion were also the same as in the first approach. The charges of united carbon atoms not bonded with nitrogen were zero.
Simulations were performed in cubic cells with the periodic boundary conditions containing 500 molecules of ionic liquids. A cutoff for short-range electrostatic and van der Waals interactions was 1.1 nm. The particle mesh Ewald method was used to compute long-range electrostatic interactions. The covalent bonds of hydrogen atoms were constrained using the LINCS algorithm.
In each molecular dynamics run, the cell was minimized and then equilibrated at an elevated temperature to prevent possible crystallization. After that, it was cooled down to 298 K and equilibrated during 1 ns. Then 50 ns of the production trajectory at the same temperature was written. Simulations were conducted in the NPT ensemble using the v-rescale algorithm for temperature control and the Parrinello–Rahman barostat for maintaining a constant pressure (1 bar). Both OPLS-AA and OPLS-UA approaches reproduce the experimental densities of liquid EAN, PAN, and BAN at 298 K within 3% uncertainty.
Test particle insertion method
In the Widom test particle insertion method, the excess chemical potential of a solute is calculated by averaging the energy of interactions of this solute over a large number of insertions into the random places of the simulation cell at different time points. The following equation is used for simulations in the NPT ensemble: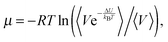 | (3) |
ΔsolvG° = μ + RT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(RT/p°Vm), ln(RT/p°Vm), | (4) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000
000![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 insertions at random positions were made into each of 50
000 insertions at random positions were made into each of 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 snapshots taken for each 1 ps of simulation (5 × 1010 insertions for each system in total).
000 snapshots taken for each 1 ps of simulation (5 × 1010 insertions for each system in total).
Using this method, we calculated the Gibbs free energies of solvation of hard spheres with two different radii, 0.28 nm and 0.33 nm, and of a molecule of methane modeled as a single united carbon atom into each ionic liquid. The radius of a larger sphere, 0.33 nm, corresponds to the radius of a cavity necessary to accommodate a methane molecule.29,30 Thus, we can obtain the energy of interactions of methane with solvent ΔintG (eqn (2)) by subtracting the energy of solvation of this sphere from the energy of solvation of methane. For two models of EAN, the Gibbs free energies of solvation of krypton (Lennard-Jones potential parameters taken from the literature31) were additionally calculated for comparison with the existing experimental data.4 The results are given in Tables 2 and 3.
| ΔsolvG°/kJ mol−1 | ΔintG/(kJ mol−1) | |||||||
|---|---|---|---|---|---|---|---|---|
| Solute | HS (σ = 0.28 nm) | HS (σ = 0.33 nm) | CH4 | CH4 | ||||
| Model | UA | AA | UA | AA | UA | AA | UA | AA |
| Solvent | ||||||||
| EAN | 30.52 | 34.87 | 40.38 | 50.86 | 23.77 | 27.49 | −16.61 | −23.36 |
| PAN | 26.94 | 30.04 | 34.85 | 41.70 | 20.08 | 22.78 | −14.76 | −18.91 |
| BAN | 24.13 | 27.67 | 28.97 | 37.43 | 15.65 | 19.76 | −13.32 | −17.67 |
| TMAN | 29.57 | — | 42.31 | — | 22.52 | — | −19.80 | — |
| TMBAN | 26.36 | 27.31 | 36.45 | 38.85 | 19.86 | 19.08 | −16.59 | −19.77 |
| Solute | ΔsolvG°/kJ mol−1 | ||
|---|---|---|---|
| UA | AA | Exp4 | |
| Kr | 22.14 | 25.43 | 20.14 |
| CH4 | 23.77 | 27.49 | 21.02 |
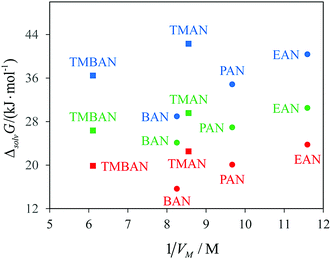
First of all, we should mention a fairly good agreement of the Gibbs free energies of solvation of methane and krypton in a united atom model with the experiment. Second, both models predict much lower Gibbs free energies of cavity formation in PILs than those in AILs. TMAN is an isomer of BAN and has almost the same value of molar volume Vm (see Fig. 4). At the same time, the Gibbs free energy of cavity formation in TMAN is larger than that in BAN and is close to that in EAN, which has a much lower molar volume. Moreover, the united atom model predicts ΔcavG in TMBAN to be close to that in PAN, while the molar volume of TMBAN is 60% higher. In an all-atom model, the cavity formation cost in TMBAN is more close to that in BAN. Third, the calculated values of ΔsolvG° for methane are also higher in AILs than in PILs. The solute–solvent interaction energy ΔintG decreases in a sequence BAN > PAN > EAN > TMAN. The intermolecular interactions of methane with AILs turn out to be even more favorable than with PILs. The cavity formation contribution is solely responsible for the unexpectedly enhanced solubility of hydrocarbons in PILs.
The lower values of the Gibbs free energy of cavity formation in PILs, in turn, evidence that solvent–solvent interactions are in average weaker in PILs than in AILs. This may seem strange since the hydrogen bonds in the considered PILs lead to an increase in energy of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 interactions between the cation and the anion, and we could also expect an additive or an even synergistic effect of Coulombic interactions and hydrogen bonds between the ions on the cost of cavity formation.
1 interactions between the cation and the anion, and we could also expect an additive or an even synergistic effect of Coulombic interactions and hydrogen bonds between the ions on the cost of cavity formation.
An explanation can be suggested from the fact of existence of polar and nonpolar domains in PILs,15 which have different solvation properties. To compare them, we tried to estimate the number of successful (no heavy atoms of solvent within the hard sphere radius) and unsuccessful (overlap of a hard sphere with some heavy atoms of ionic liquid molecules) insertions of hard spheres in test particle insertion calculations into polar and apolar domains separately. If the heavy atom nearest to the center of the randomly inserted hard sphere was a carbon, the insertion was considered to fall into the apolar domain, and if it was one of the nitrogens or oxygens – into the polar domain. Despite this being quite a loose definition of domains, the tendency of a much lower probability of successful insertion into a polar part than into an apolar part is clearly demonstrated. For example, among all insertions into the OPLS-UA model of EAN, 65% hit the polar domain. This number has a physical meaning of the fraction of space occupied by the polar domain (according to our definition) in the neat ionic liquid. At the same time, among all successful insertions of a hard sphere with r = 0.33 nm, only 12.9% are found in the polar domain and the rest 87.1% in the apolar domain. An increase in size of the apolar domain from EAN to BAN leads to a further decrease in the fraction of successful insertions that hit the polar domain (Table 4).
| r (nm) | Solvent | Fraction of successful insertions that hit the polar domain | Fraction of all insertions that hit the polar domain | ΔΔG/kJ mol−1 |
|---|---|---|---|---|
| 0.28 | EAN | 0.202 | 0.650 | 5.0 |
| PAN | 0.120 | 0.552 | 5.5 | |
| BAN | 0.069 | 0.462 | 6.1 | |
| 0.33 | EAN | 0.129 | 0.650 | 6.3 |
| PAN | 0.079 | 0.552 | 6.6 | |
| BAN | 0.034 | 0.462 | 7.9 |
The probabilities of insertion can be related to the chemical potentials of hard spheres in each domain, if we ignore volume fluctuations in eqn (3):
μ = −RT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) p, p, | (5) |
ΔΔG(apolar → polar) = RT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(papolar/ppolar). ln(papolar/ppolar). | (6) |
Conclusions
Protic ionic liquids, which is an insufficiently well-studied group of ionic liquids, is found to exhibit unexpected solvation properties. The solubility of hydrocarbons in alkylammonium nitrate PILs is better than that in AILs with a similar or even higher molar volume. This fact is explained by a lower free energy cost of cavity formation in PILs. The existence of polar and apolar domains in alkylammonium PILs leads to the preferential cavity formation and solvation of hydrocarbons in apolar domains with relatively low values of ΔsolvG°.As a consequence, the considered PILs perform worse than AILs in aliphatic/aromatic hydrocarbon separation and can be described as featuring weaker solvophobic effects. Further comparison of various solvent properties of protic and aprotic ionic liquids will be an interesting task. It is important to choose liquids with similar molar volumes for correct comparison, but even for BAN it is lower than that of the usual AILs, while alkylammonium nitrates with longer alkyl chains are solid substances at room temperature. This difficulty can be overcome by the extrapolation of molar volume-dependent properties or by choosing PILs with different anions and/or cations.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
We thank Dr Alexander Klimovickij and Dr Marat Ziganshin for their help in measuring the IR spectra and DSC curves. We also thank the reviewers for their valuable comments that helped to improve the quality of the paper. This work was performed according to the Russian Government Program of Competitive Growth of Kazan Federal University. B. N. S. thanks the Ministry of Education of Russia.Notes and references
- T. L. Greaves and C. J. Drummond, Protic Ionic Liquids: Properties and Applications, Chem. Rev., 2008, 108, 206–237 CrossRef CAS PubMed.
- P. Walden, Molecular weights and electrical conductivity of several fused salts, Bull. Acad. Imp. Sci. St. – Petersbourg, 1914, 8, 405–422 Search PubMed.
- S. P. Verevkin, D. H. Zaitsau, B. Tong and U. Welz-Biermann, New for old. Password to the thermodynamics of the protic ionic liquids, Phys. Chem. Chem. Phys., 2011, 13, 12708 RSC.
- D. F. Evans, S.-H. Chen, G. W. Schriver and E. M. Arnett, Thermodynamics of solution of nonpolar gases in a fused salt. Hydrophobic bonding behavior in a nonaqueous system, J. Am. Chem. Soc., 1981, 103, 481–482 CrossRef CAS.
- L. M. C. Oliveira, F. R. G. Ribeiro, M. L. Alcantara, G. O. Pisoni, V. F. Cabral, L. Cardozo-Filho and S. Mattedi, High pressure vapor-liquid equilibria for binary methane and protic ionic liquid based on propionate anions, Fluid Phase Equilib., 2016, 426, 65–74 CrossRef CAS.
- W. Afzal, B. Yoo and J. M. Prausnitz, Inert-Gas-Stripping Method for Measuring Solubilities of Sparingly Soluble Gases in Liquids. Solubilities of Some Gases in Protic Ionic Liquid 1-Butyl, 3-Hydrogen-imidazolium Acetate, Ind. Eng. Chem. Res., 2012, 51, 4433–4439 CrossRef CAS.
- L. Wright, M. W. Sanders, L. Tate, G. Fairless, L. Crowhurst, N. C. Bruce, A. J. Walker, G. A. Hembury and S. Shimizu, Hydrophilicity, the major determining factor influencing the solvation environment of protic ionic liquids, Phys. Chem. Chem. Phys., 2010, 12, 9063 RSC.
- I. A. Sedov and B. N. Solomonov, Thermodynamic description of the solvophobic effect in ionic liquids, Fluid Phase Equilib., 2016, 425, 9–14 CrossRef CAS.
- I. A. Sedov, M. A. Stolov and B. N. Solomonov, tert-Butyl chloride as a probe of the solvophobic effects, Fluid Phase Equilib., 2014, 382, 164–168 CrossRef CAS.
- D. H. Zaitsau, V. N. Emel’yanenko, P. Stange, C. Schick, S. P. Verevkin and R. Ludwig, Dispersion and Hydrogen Bonding Rule: Why the Vaporization Enthalpies of Aprotic Ionic Liquids Are Significantly Larger than those of Protic Ionic liquids, Angew. Chem., Int. Ed., 2016, 55, 11682–11686 CrossRef CAS PubMed.
- V. N. Emel’yanenko, G. Boeck, S. P. Verevkin and R. Ludwig, Volatile Times for the Very First Ionic Liquid: Understanding the Vapor Pressures and Enthalpies of Vaporization of Ethylammonium Nitrate, Chem. – Eur. J., 2014, 20, 11640–11645 CrossRef PubMed.
- R. Atkin and G. G. Warr, The Smallest Amphiphiles: Nanostructure in Protic Room-Temperature Ionic Liquids with Short Alkyl Groups, J. Phys. Chem. B, 2008, 112, 4164–4166 CrossRef CAS PubMed.
- Y. Umebayashi, W.-L. Chung, T. Mitsugi, S. Fukuda, M. Takeuchi, K. Fujii, T. Takamuku, R. Kanzaki and S. Ishiguro, Liquid Structure and the Ion–Ion Interactions of Ethylammonium Nitrate Ionic Liquid Studied by Large Angle X-Ray Scattering and Molecular Dynamics Simulations, J. Comput. Chem., Jpn., 2008, 7, 125–134 CrossRef CAS.
- R. Hayes, S. Imberti, G. G. Warr and R. Atkin, Effect of Cation Alkyl Chain Length and Anion Type on Protic Ionic Liquid Nanostructure, J. Phys. Chem. C, 2014, 118, 13998–14008 CAS.
- R. Hayes, S. Imberti, G. G. Warr and R. Atkin, Amphiphilicity determines nanostructure in protic ionic liquids, Phys. Chem. Chem. Phys., 2011, 13, 3237–3247 RSC.
- X. Song, H. Hamano, B. Minofar, R. Kanzaki, K. Fujii, Y. Kameda, S. Kohara, M. Watanabe, S. Ishiguro and Y. Umebayashi, Structural Heterogeneity and Unique Distorted Hydrogen Bonding in Primary Ammonium Nitrate Ionic Liquids Studied by High-Energy X-ray Diffraction Experiments and MD Simulations, J. Phys. Chem. B, 2012, 116, 2801–2813 CrossRef CAS PubMed.
- I. A. Sedov, M. A. Stolov and B. N. Solomonov, Thermodynamics of solvation in propylene glycol and methyl cellosolve, J. Chem. Thermodyn., 2014, 78, 32–36 CrossRef CAS.
- I. A. Sedov, T. I. Magsumov and B. N. Solomonov, Solvation of hydrocarbons in aqueous–organic mixtures, J. Chem. Thermodyn., 2016, 96, 153–160 CrossRef CAS.
- K. Růžička and V. Majer, Simultaneous Treatment of Vapor Pressures and Related Thermal Data Between the Triple and Normal Boiling Temperatures for n-Alkanes C5–C20, J. Phys. Chem. Ref. Data, 1994, 23, 1–39 CrossRef.
- A. Marciniak, Influence of cation and anion structure of the ionic liquid on extraction processes based on activity coefficients at infinite dilution. A review, Fluid Phase Equilib., 2010, 294, 213–233 CrossRef CAS.
- S. P. Verevkin, V. N. Emel’yanenko, I. Krossing and R. Kalb, Thermochemistry of ammonium based ionic liquids: Tetra-alkyl ammonium nitrates – Experiments and computations, J. Chem. Thermodyn., 2012, 51, 107–113 CrossRef CAS.
- T. L. Greaves and C. J. Drummond, Ionic liquids as amphiphile self-assembly media, Chem. Soc. Rev., 2008, 37, 1709 RSC.
- D. Chandler, Interfaces and the driving force of hydrophobic assembly, Nature, 2005, 437, 640–647 CrossRef CAS PubMed.
- R. Godawat, S. N. Jamadagni and S. Garde, Characterizing hydrophobicity of interfaces by using cavity formation, solute binding, and water correlations, Proc. Natl. Acad. Sci. U. S. A., 2009, 106, 15119–15124 CrossRef CAS PubMed.
- B. Widom, Some Topics in the Theory of Fluids, J. Chem. Phys., 1963, 39, 2808–2812 CrossRef CAS.
- F. V. Grigoriev, M. V. Basilevsky, S. N. Gabin, A. N. Romanov and V. B. Sulimov, Cavitation Free Energy for Organic Molecules Having Various Sizes and Shapes, J. Phys. Chem. B, 2007, 111, 13748–13755 CrossRef CAS PubMed.
- J. N. Canongia Lopes and A. A. H. Pádua, Molecular Force Field for Ionic Liquids Composed of Triflate or Bistriflylimide Anions, J. Phys. Chem. B, 2004, 108, 16893–16898 CrossRef.
- W. L. Jorgensen and J. Gao, Monte Carlo simulations of the hydration of ammonium and carboxylate ions, J. Phys. Chem., 1986, 90, 2174–2182 CrossRef CAS.
- F. Sedlmeier, D. Horinek and R. R. Netz, Entropy and enthalpy convergence of hydrophobic solvation beyond the hard-sphere limit, J. Chem. Phys., 2011, 134, 55105 CrossRef PubMed.
- S. Garde, G. Hummer, A. E. García, M. E. Paulaitis and L. R. Pratt, Origin of Entropy Convergence in Hydrophobic Hydration and Protein Folding, Phys. Rev. Lett., 1996, 77, 4966–4968 CrossRef CAS PubMed.
- B. Guillot and Y. Guissani, A computer simulation study of the temperature dependence of the hydrophobic hydration, J. Chem. Phys., 1993, 99, 8075–8094 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Comparison of the measured physical properties of synthesized ionic liquids with the literature data. See DOI: 10.1039/c7cp05249a |
| This journal is © the Owner Societies 2017 |