Unravelling redox processes of Li7MnN4 upon electrochemical Li extraction–insertion using operando XAS†
Abstract
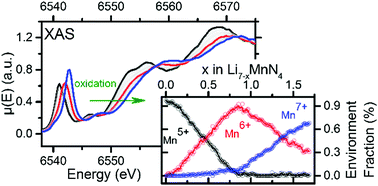
A large data set of XAS (X-ray Absorption Spectroscopy) Manganese K-edge spectra has been collected operando and studied upon the electrochemical oxidation of the promising Li-ion battery anode material Li7MnN4. Using chemometric tools such as PCA (Principal Component Analysis) and MCR-ALS (Multivariate Curve resolution – Alternating Least Squares), three independent environment spectra were insulated. Based on the faradaic yield and well-chosen comparison of absorption spectrum energies within the frame of the coordination charge model, these environments were ascribed to unusual oxidation states allowed by nitride chemistry at a low potential (∼1.2 V vs. Li+/Li), i.e. Mn5+ (3d2), Mn6+ (3d1) and Mn7+ (3d0). Also, their relative amounts are discussed with regard to the long-range structural variation which can be simply described by two successive biphasic domains followed by a solid-solution behaviour. Gathering this long-range and local structure information provides a complete picture of the redox mechanisms occurring in Li7MnN4.
- This article is part of the themed collection: 2017 PCCP HOT Articles


 Please wait while we load your content...
Please wait while we load your content...