Signatures of a quantum diffusion limited hydrogen atom tunneling reaction†
Morgan E.
Balabanoff
,
Mahmut
Ruzi
 and
David T.
Anderson
and
David T.
Anderson
 *
*
Department of Chemistry, University of Wyoming, Laramie, WY 82071, USA. E-mail: danderso@uwyo.edu
First published on 30th November 2017
Abstract
We are studying the details of hydrogen atom (H atom) quantum diffusion in highly enriched parahydrogen (pH2) quantum solids doped with chemical species in an effort to better understand H atom transport and reactivity under these conditions. In this work we present kinetic studies of the 193 nm photo-induced chemistry of methanol (CH3OH) isolated in solid pH2. Short-term irradiation of CH3OH at 1.8 K readily produces CH2O and CO which we detect using FTIR spectroscopy. The in situ photochemistry also produces CH3O and H atoms which we can infer from the post-photolysis reaction kinetics that display significant CH2OH growth. The CH2OH growth kinetics indicate at least three separate tunneling reactions contribute; (i) reactions of photoproduced CH3O with the pH2 host, (ii) H atom reactions with the CH2O photofragment, and (iii) long-range migration of H atoms and reaction with CH3OH. We assign the rapid CH2OH growth to the following CH3O + H2 → CH3OH + H → CH2OH + H2 two-step sequential tunneling mechanism by conducting analogous kinetic measurements using deuterated methanol (CD3OD). By performing photolysis experiments at 1.8 and 4.3 K, we show the post-photolysis reaction kinetics change qualitatively over this small temperature range. We use this qualitative change in the reaction kinetics with temperature to identify reactions that are quantum diffusion limited. While these results are specific to the conditions that exist in pH2 quantum solids, they have direct implications on the analogous low temperature H atom tunneling reactions that occur on metal surfaces and on interstellar grains.
1. Introduction
Hydrogen atom (H atom) adsorption and diffusion are important in many chemical environments such as heterogeneous catalysis,1 condensed phase astrochemistry,2–4 and hydrogen storage materials.5 There are a variety of H atom diffusion regimes based on the corrugation of the translational potential energy surface and the temperature at which diffusion occurs. Our interest lies in the regime of homogeneous periodic potential corrugations and extreme low temperatures where the diffusion of the H atom is inherently quantum mechanical. Specifically, we are studying the quantum diffusion of H atoms in solid parahydrogen (pH2) in the temperature range between 1.7 and 4.3 K. In this temperature range we have observed new types of chemical behavior for reactions that involve H atoms. The basic premise of our work is that the H atom diffusion mechanism in solid pH2 is somewhat unique and thus should lead to new types of diffusion limited reaction kinetics. In some cases we have observed tunneling reactions that only occur with appreciable yields below a certain critical temperature.6–8 For reactions of H atoms with formic acid conducted in solid pH2 at low temperature7,8 we observed qualitatively different reaction products than the analogous reactions conducted in rare gas matrix studies9 at slightly higher temperatures suggesting the tunneling reactions in solid pH2 are occurring under a different diffusional regime. A deeper understanding of the mesoscopic diffusion of H atoms in solid pH2 is needed to unify a variety of seemingly disparate experimental observations. Further, understanding H atom quantum diffusion limited chemistry in solid pH2 at a predictive level may also allow us to control a variety of low temperature H atom diffusion phenomena.It is believed10–19 that H atoms tunnel between adjacent lattice sites in solid pH2 by a chemical mechanism that is based on the simplest chemical reaction, H + H2 → H2 + H. Given that the activation barrier20 for this chemical reaction is 9.60 kcal mol−1 (3360 cm−1), at low temperature the only way the H atom can “quantum diffuse” is by repeated tunneling jumps through the reaction barrier. From a chemistry perspective, this means that H atom reactions with chemical dopants in solid pH2 can continue to occur even at the lowest achievable temperatures because the H atom retains its mobility through quantum effects (tunneling). Evidence of quantum diffusion in surface studies is usually provided by the observation of temperature independent diffusion rates.21 The transition at low temperature from classical thermally activated hopping (Arrhenius-type temperature dependence) to quantum tunneling (temperature independent) typically occurs in the range of 60–140 K for H atoms on metal surfaces.22 Observation over such a large temperature range is not possible in solid pH2 where the solid starts to rapidly sublime at temperatures above 5 K. Similarly, H atom reaction studies conducted in rare gas matrices can only be conducted over limited temperature ranges, but usually the H atoms only diffuse at appreciable rates in the classical thermal hopping range.9 The chemical physics in the quantum diffusion range should be distinct from the thermal hopping regime because the diffusion is governed by quantum mechanical phenomena. We therefore expect that quantum diffusion limited chemistry of H atoms with other chemical species in solid pH2 will show both interesting temperature effects and reaction products. Indeed, we have now documented a series of H atom reactions with N2O, HCOOH, and NO that show novel temperature effects and products.6–8,23
In this study we focus on investigating reactions of H atoms with methanol (CH3OH). The photochemistry and low temperature surface reactions of this chemical system (H + CO) have been well studied due the abundance of CH3OH in a variety of astronomical environments.4,24 To do this we rely on the 193 nm in situ photochemistry of methanol (CH3OH) in solid pH2 to generate H atoms. At this photon energy there are five open dissociation channels, namely,25,26
| CH3OH + hν(193 nm) → CH3O + H | (1a) |
| → CH2OH + H | (1b) |
| → CH3 + OH | (1c) |
| → CH2 + H2O | (1d) |
| → CH2O + H2 | (1e) |
| CH3O + H2 → CH3OH + H → CH2OH + H2 | (2) |
Our interest in the 193 nm in situ photochemistry of CH3OH in solid pH2 is motivated by our desire to study the H + CH3OH → CH2OH + H2 tunneling reaction.28,31 As discussed, if photochannel (1a) is dominant, along with the generation of CH3O is the production of H atoms. Further, because some of the primary photolysis products (CH3O and CH2OH) are also photolabile at 193 nm, there can be additional H atom production from secondary photolysis events. We can test for the presence of H atoms using the tunneling reaction of H atoms with CH3OH to produce CH2OH. By conducting these photolysis experiments such that CH3OH is the most concentrated species after photolysis, repeated FTIR scans after photolysis can be used to indirectly monitor the H atom concentration via the tunneling reaction with CH3OH. We can study the reaction kinetics as a function of temperature over the experimental range (1.7 to 4.3 K) to further explore the details of H atom quantum diffusion. That is, because the H + CH3OH reaction is a bimolecular reaction that requires both reactants to be in adjacent lattice sites to react, the reaction kinetics are likely controlled by how fast and to what extent the two reaction partners diffuse next to each other. As we will show, reactions that rely on H atom quantum diffusion to occur can display anomalous temperature effects. Specifically, this type of reaction may only occur at low temperature and not at high temperature over this small range. This can be the result of changes in the microscopic details of H atom quantum diffusion over this small temperature range. Specifically, non-resonant tunneling jumps can be accommodated by one- and two-phonon processes that might steer the H atom differently towards a potential reaction partner.32–34 This is still an active area of research and in these studies we will show evidence for H atom reactions with CH3OH that only occur at 1.8 K, and not 4.3 K.
2. Experimental details
Our experimental apparatus is described in detail elsewhere;35 briefly, we grow millimeters thick, chemically doped pH2 crystals via co-deposition of independent gas streams of dopant (CH3OH) and pH2 host onto a BaF2 optical substrate maintained at approximately 2.5 K inside a liquid helium bath cryostat. The pH2 host in these studies is enriched to 99.97% pH2 levels using a variable temperature ortho/para catalytic converter operated near 14.0 K. FTIR spectroscopy is performed on the sample using a normal incidence transmission optical setup. The measured integrated intensities of specific solid pH2 IR absorptions36–38 allow us to determine the IR path length through the sample, which permits the concentration of different species within the crystal to be determined using the Beer's Law expression,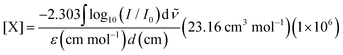 | (3) |
Photolysis is achieved using the 193 nm output of an ArF excimer laser (Gam Laser EX5) configured to pass through the sample at an angle of 45° with respect to substrate surface normal. This optical setup permits FTIR spectra to be recorded within the photolyzed region of the crystal either during or immediately after 193 nm irradiation. The typical experimental procedure is to photolyze a CH3OH/pH2 sample at a specified temperature for a short period of time and then record repeated FTIR spectra with short acquisition times to measure the ensuing low temperature kinetics. In this study we used two different FTIR configurations. To characterize the as-deposited sample we used a liquid nitrogen cooled InSb detector to record the spectrum from 1800–5000 cm−1 at 0.05 cm−1 resolution. To characterize the kinetics, we used a liquid nitrogen cooled HgCdTe detector for the range from 600 to 4900 cm−1 at a resolution of 0.05 cm−1 with a 5500 cm−1 low pass filter in the IR beam. In this study we did not explicitly check for the effects of the FTIR beam on the measured kinetics; however, previous studies have shown that the decay of CH3O is not induced by IR irradiation.30 The time resolution of the FTIR spectra used to map out the kinetics therefore is controlled by how many scans are averaged together and the resolution. For example, the methanol system required a time resolution of 41.3 s (4 co-added scans at 0.05 cm−1 resolution) for one of the fastest post-photolysis reactions measured in this study.
We employed the GAUSSIAN 09 program40 to perform geometry and harmonic vibrational calculations on CH2OH for all possible hydrogen and deuterium isotopomers. We conducted both MP2 and density functional calculations with Dunning's correlation-consistent polarized-valence triple-zeta (cc-pVTZ or aug-cc-pVTZ) basis sets.41,42 These data are presented in the ESI,† in Tables S2–S10.
3. Results and discussion
One of the first steps in any photolysis study is the spectroscopic assignment of all the various species involved, and most importantly the photolysis products that may be unstable otherwise. In this case, we had published spectra for a variety of the species involved (CH3OH, CO, CHO)7,43–45 but needed assigned peaks for all possible deuterium isotopomers of CH2OH, CH3OH and CH2O. For convenience we list the various peaks used to determine species concentrations in Table S1 (ESI†). All the initial vibrational assignments of CH2OH were carried out by comparison to B3LYP harmonic vibrational frequency and intensity calculations, gas phase literature values where available,46,47 and Ar matrix isolation studies.48,49 During the course of this work Lee and co-workers published29,30 vibrational assignments for CH2OH and CD2OH isolated in solid pH2 at 3.2 K. Note this previous work did not report observation of CD2OD and the reasons for this will become clear in this study. We present all the peaks assigned to CH2OH, CD2OD, and CD2OH in Tables S11–S13 (ESI†) along with representative spectra of CH2OH in Fig. S2 in the ESI.†3.1 Photolysis studies of CH3OH/pH2
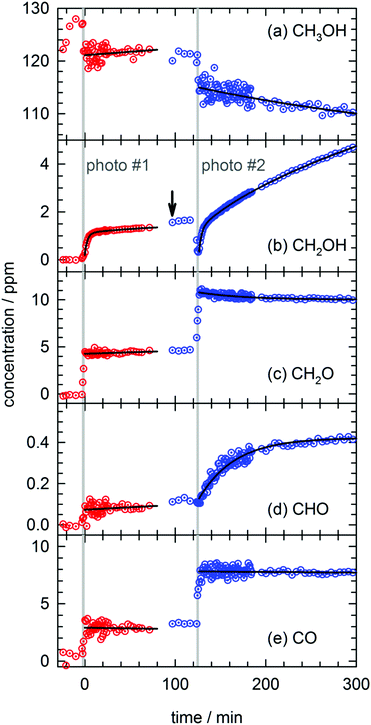
In total four separate photolysis experiments were conducted on as-deposited CH3OH/pH2 samples at ∼1.8 K with initial CH3OH concentrations ranging from 75 to 120 ppm. Representative FTIR spectra of CH3OH, CH2OH, CH2O, CHO, and CO are presented in Fig. S3 in the ESI† at different stages of the photolysis experiment (Expt. #4). The full kinetic data for all four low temperature photolysis experiments is shown in Fig. S4 in the ESI.† The kinetic data for the photolysis experiment (Expt. #4) recorded with the highest time resolution is shown in Fig. 2. The grey vertical bar in Fig. 2 represents the timing and duration of the 193 nm photolysis exposure. After deposition is complete, FTIR spectra are recorded to characterize the CH3OH concentration prior to photolysis (117(1) ppm indicated by dashed red line in Fig. 2). What is clear from Fig. 2 is that even after the photolysis laser is shut off, a variety of chemical reactions continue to occur even at 1.84(1) K.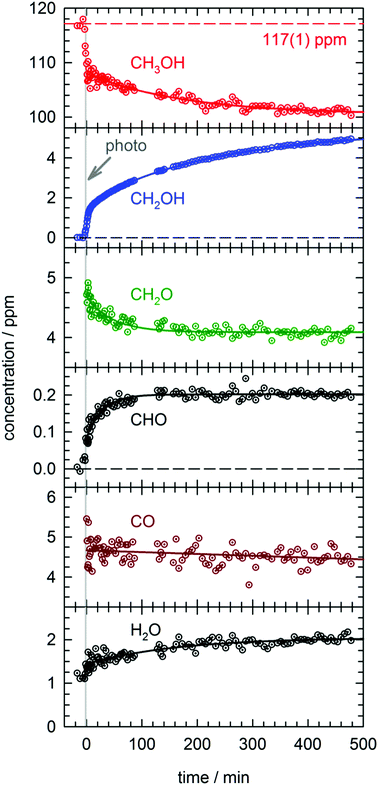 | ||
| Fig. 2 Kinetic plots for a 193 nm photolysis experiment (Expt. #4) conducted on a CH3OH/pH2 sample at 1.84(1) K. The photolysis exposure (3 min, 80 Hz, 19 mW cm−2) is indicated by the grey vertical bar. The data are represented by dotted circles, and the lines are the results of least-squares fits of the data to eqn (4) or (5), except the CH2OH data that is fit to the sum of three first-order processes (see text for details). | ||
We will first characterize the photolysis step. In the four photolysis experiments performed in this study the general findings are (1) the CH3OH photolysis follows first-order kinetics with a quantum yield of Φ = 0.14(1), (2) the major photolysis products are CO and CH2O in a concentration ratio of [CO]/[CH2O] = 1.1(1) and (3) there is a 13(9)% systematic overestimation in the concentration of the photoproducts (CO + CH2O) compared to the decay in the CH3OH precursor concentration. Using the published cross section50 for CH3OH at 193 nm and the measured UV fluence and exposure time, the determined quantum yield is consistent with the photolysis quantum yields of other small molecules measured by this lab27,51 (see Fig. S5, ESI† for analysis) and illustrates the weak cage effect of solid pH2. The photo-induced production of CO indicates a significant amount of secondary photolysis is occurring under these conditions as none of the primary photochannels produce CO (see eqn (1)). We note that in addition to CO and CH2O there is minor production (<10%) of CH4 which can arise from CH2 production (CH2 + H2 → CH4). Given the uncertainties in the measured concentrations of each species, getting the concentrations to agree to within ±20% is an adequate level of agreement. We point out that the CH3OH concentration is determined using the ν1 OH stretching vibration. This CH3OH feature has a complicated lineshape (see Fig. S3, ESI†) thereby making systematic errors in the CH3OH concentration likely larger. In the experiment shown in Fig. 2 we observe only minor photoproduction of H2O (<1 ppm), however, H2O is difficult to characterize because H2O is present in the vacuum gas surrounding the crystal. Examination of Fig. S4 (ESI†) shows that for most experiments there is zero-order growth in the H2O concentration due to continued deposition of gas phase H2O. However, we find no evidence of H2O satellite peaks52,53 or ortho-H2O immediately54 after the photolysis laser is stopped indicating that H2O is not produced at significant levels by the in situ photolysis of CH3OH. The negligible H2O production is consistent with the gas phase photochemistry that shows channel (1d) is a minor channel and experiments conducted on CD3OD (to be shown) which display only minor production of D2O.
What is striking about the kinetic traces in Fig. 2 is the amount of chemistry that occurs well after the photolysis laser is shut off. For example, the CH3OH concentration continues to decrease by 7.0(3)% over the full post-photolysis reaction period (approximately 500 minutes). This post-photolysis behavior in the CH3OH concentration can be quantified by fitting the data to a single exponential decay function,
[X] = [X]∞ + A![[thin space (1/6-em)]](https://www.rsc.org/images/entities/i_char_2009.gif) exp(−kt) exp(−kt) | (4) |
For the two major photoproducts CO and CH2O, the kinetic behavior after photolysis is qualitatively different. Surprisingly, a clear decrease in the CO concentration after photolysis is not observed. The fitted line in Fig. 2 for the CO data is just the equation of a straight line (y = mx + b) and it shows almost no change in the CO concentration (a slight decrease). In contrast, the CH2O concentration decays immediately after photolysis with a first-order decay constant. The CH2O data are fit to eqn (4) and the extracted parameters are shown in Table S15 (ESI†). CH2O decays with a significantly greater average rate constant (kAVG = 1.8(4) × 10−2 min−1) than CH3OH. However, we believe the CH2O decays for the same reason as CH3OH, reactions with H atoms. We will discuss the CH2O decay in more detail, but we assert it is faster because it involves local migration of H atoms to photo-produced CH2O.
The two species that continue to grow after photolysis are CHO and CH2OH. The CHO growth after photolysis is fit to the following expression,
| [X] = [X]0 + A[1 − exp(−kt)] | (5) |
| H + CH2O → H2 + CHO | (6a) |
| → CH2OH | (6b) |
We will return to the discussion of why the rate constant for eqn (6) is significantly larger than the rate constant extracted from the CH3OH data in the Discussion section. We want to point out that comparing first-order rate constants is not affected by systematic errors in the concentration determinations. Clearly, we check the proposed mechanisms by verifying that the amount of products equals the loss in reactants, but these comparisons are only as good as the determined absolute concentrations. By “matching” rate constants we provide a more reliable way to infer the elementary tunneling reaction steps that are occurring under these conditions. The proposed mechanism reported in eqn (6) thereby suggests that we might also measure a contribution to the growth of CH2OH that has a first-order rate constant in the range measured for CH2O decay. Examination of Fig. 1b shows that this reaction can occur by H atom addition to CH2O (however with a higher reaction barrier).
By far the most complex kinetic behavior is displayed by the growth of the CH2OH species. As shown in Fig. 2, right after photolysis there is rapid growth in the CH2OH concentration that is right at the limit of the time resolution of the repeated FTIR spectra. Then the CH2OH growth transitions into a slower increase that continues for the full length of the experiment. The high quality of the CH2OH data allows us to fit the growth to an expression that contains three separate first-order rate expressions. The total fitted expression is shown as a blue line in Fig. 2 and the individual fitted components are shown in an expanded view in Fig. 3. There is a fast process with an average (excluding experiment #1 which was recorded with too slow a time resolution) rate constant k1 = 0.35(1) min−1 that happens right after the photolysis laser is stopped. The value of this extracted rate constant is very close to the rate constant determined by Lee and co-workers (k = 0.46(2) min−1) for the decay in the CH3O concentration after photolysis of CH3ONO at 3.2 K.30 Thus, we assign the fast component of the CH2OH growth to reactions of CH3O with the pH2 host. The medium rate growth process has an average rate constant of k2 = 1.7(6) × 10−2 min−1 and is assigned to reactions of H atoms with CH2O according to eqn (6b). Finally, the slowest process that accounts for 74.1% of the post photolysis growth of CH2OH occurs with an average rate constant k3 = 4.0(5) × 10−3 min−1. We assign this process to reactions of H atoms with CH3OH because the k3 rate constant is very close to the rate constant for the CH3OH decay (k = 6.1(10) × 10−3 min−1) as it must be if we are observing a single elementary step, i.e., H + CH3OH → H2 + CH2OH. This reaction continues to occur over the full 500 min reaction time. We assert that the H + CH3OH → H2 + CH2OH reaction is quantum diffusion limited. We point out that the extracted k3 rate constant is very similar to the average rate constant (k = 4.9(7) × 10−3 min−1) measured for the H + HCOOH → H2 + HOCO reaction studied previously7 in solid pH2 at 1.9 K that we also claim is quantum diffusion limited. As discussed previously, this slow process is the most interesting because we believe it occurs via long-range migration of H atoms.
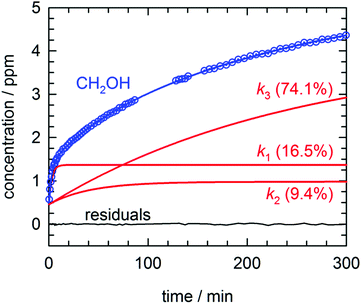 | ||
| Fig. 3 Expanded view of the early time growth kinetics of CH2OH for the experiment depicted in Fig. 2. A fit to the data consisting of three first-order processes is shown as a solid blue line, the three individual first-order components to the CH2OH growth are plotted as solid red lines (labeled by the rate constant and percent final concentration), and the residuals from the fit are plotted as a solid black line. See text for details. | ||
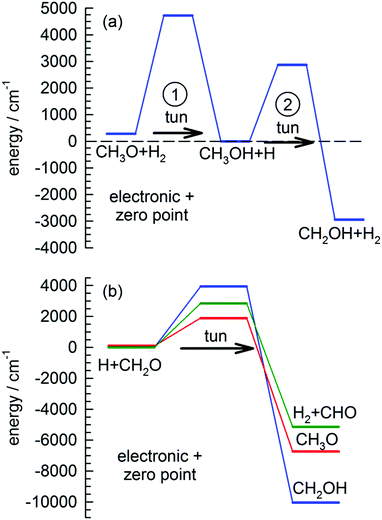
We want to explore the fast growth in the CH2OH concentration observed immediately after photolysis a little further. This reaction has been studied extensively theoretically due to its importance in methanol combustion chemistry.31,61,62 Shown in Fig. 1(a) is the best ab initio estimates28 for the reaction barriers (ΔV00) and enthalpy of reaction (ΔH00) at 0 K for the two reactions involved in the conversion of CH3O to CH2OH in solid pH2. In the proposed tunneling mechanism, CH3O reacts with a neighboring pH2 molecule to form CH3OH and an H atom. This reaction step involves tunneling through a 4440 cm−1 barrier and is almost thermo-neutral depositing about 280 cm−1 to the reaction products. Then because the two products are produced in adjacent lattice sites and solid pH2 can efficiently dissipate the reaction energy, they undergo a second tunneling reaction (ΔV00 = 2870 cm−1) to form CH2OH and H2. This two-step tunneling mechanism is relatively fast because the first tunneling reaction is for a dopant reacting with the pH2 host and therefore the reaction does not require diffusion of the reactants to occur.
3.2 Photolysis studies of CD3OD/pH2
The assignment of the CH2OH growth process with the fast rate constant (k1) to the reaction of CH3O with the pH2 host is clearly speculative because we never observe CH3O directly. We would likely have to alter the photolysis conditions significantly to observe CH3O directly because CH3O is only a minor product in the 193 nm in situ photolysis of CH3OH in pH2 and CH3O does not have any strong absorptions (greatest ∼13.0 km mol−1) in the infrared.30 In the previous studies by Lee and co-workers that detected CH3O,30 they utilized 1000 ppm concentrations of the precursor (CH3ONO) and irradiated the sample for 150 s and recorded the spectrum immediately after irradiation with acquisition times of ∼25 s. However, we can test this assignment using CD3OD as a precursor. If we re-write reaction (2) starting with fully deuterated CD3O,| CD3O + H2 → CD3OH + H → CD2OH + HD, | (7) |
To test our interpretations of the CH2OH kinetic data we conducted three additional photolysis experiments using fully deuterated methanol (CD3OD). First, we need to characterize the concentration of various deuterated methanol isotopomers to look for the possibility of isotopic scrambling prior to photolysis. We detect absorption features for the CD3OD/pH2 samples in both the O–D and O–H stretching regions, indicating that some scrambling has occurred for the hydroxyl deuterium atom. However, only minor scrambling (if any) of the methyl deuterium atoms was detected. Using Ar matrix infrared data63 for the various deuterium isotopomers of methanol, we expect medium to strong infrared absorptions in the 2800 to 3000 cm−1 region for various C–H stretching modes of CHD2OH, CHD2OD, CH2DOH and CH2DOD. As shown in Fig. S6 in the ESI,† if we examine this region for both the CH3OH/pH2 and CD3OD/pH2 samples, prominent C–H stretching peaks are only observed for the CH3OH/pH2 sample. For the CD3OD/pH2 sample, the only absorption in this region is due to the O–D stretching vibration of CD3OD near 2709.65 cm−1. Note that the absorption near 2612.76 cm−1 in Fig. S6 (ESI†) is due to the hydrogen bonded O–D stretch of the CD3OD dimer.64 Even at 10 times the magnification, only very small absorptions are measured in the expected C–H stretching region. We take this as evidence that the only methanol isotopomers at appreciable concentrations prior to photolysis are CD3OD and CD3OH. This scrambling likely occurs in the metal sample holder attached to the dopant vacuum manifold prior to deposition.
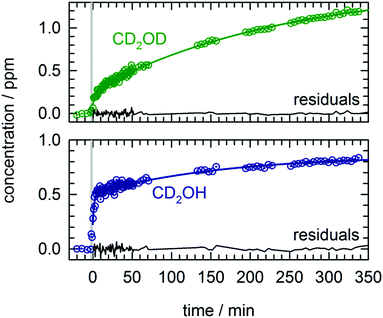
We performed the first CD3OD photolysis experiment in an analogous fashion as the CH3OH/pH2 photolysis experiments on a low temperature, as-deposited sample. We can monitor the growth of CD2OH and CD2OD separately using the corresponding CO stretch peaks near 1200 cm−1 that are shown in Fig. S7 in the ESI.† The kinetic behavior of the CD2OD and CD2OH isotopomers are qualitatively different and provide further support for the mechanistic interpretations of the CH2OH kinetic data. The full kinetic data for all species are shown in Fig. S8 in the ESI;† we present expanded views of the kinetic data after the first photolysis for CD2OD and CD2OH in Fig. 4. We fit both isotopomers to a sum of two first-order growth expressions and find clear differences between the two growth curves. For CD2OH, we observe 45% production via a fast process and 55% via a slow process. Thus, as predicted by mechanism (7) we observe fast growth in CD2OH after photolysis consistent with rapid tunneling reactions of CD3O with the pH2 host. In contrast, the importance of this fast growth process is much diminished in CD2OD, although not completely absent. For CD2OD, we observe 12% production via a fast process and 88% via a slow process. As we show in Fig. S8 (ESI†), in a second photolysis exposure of the same CD3OD/pH2 sample the amount of this fast process for CD2OD was even more diminished. Further, for both species the rate constant extracted from the slow growth process quantitatively matches the rate constant extracted for the slow growth of CH2OH. We take this as evidence that for all three hydroxymethyl isotopomers (CH2OH, CD2OH, CD2OD) the slow growth is caused by reactions of mobile H atoms with the corresponding methanol isotopomers (CH3OH, CD3OH, CD3OD). The reason the extracted rate constants are all approximately the same is because the rate is determined by the rate of H atom quantum diffusion to the reactive partner. We note that in these deuterated methanol experiments the photoproduction of CD2O is much less (about a factor of two less) suggesting that H atom reactions with CD2O should be less important to the CD2OH kinetics and that is why the CD2OH growth kinetics can be well fit with just two first-order rates.
3.3 Temperature dependence of the photoinduced kinetics
We want to measure the temperature dependence of the observed photo-induced kinetics as a further test of which reactions are quantum diffusion limited. In Fig. 5 we show the results of two separate photolysis exposures conducted on the same CH3OH/pH2 sample. We deposit the CH3OH/pH2 sample as usual and then raise the temperature to 4.3 K prior to photolysis. We allow the sample to equilibrate at 4.34 K for approximately 10 min. As can be seen in Fig. 5, at 4.34 K we measure a decrease in the CH3OH concentration with photolysis and production of CH2O and CO similar to the photolysis experiments conducted at low temperature (∼1.8 K). The relative amounts of CO and CH2O are slightly different from the low temperature photolysis, but we detect the same major photoproducts. However, the contribution to the growth of CH2OH from the slow k3 process is now completely absent and post-photolysis changes in the CH2O and CHO products are not observed. The CH2OH data after photolysis #1 can be fit to an expression that contains only two first-order rate constants. The results of this fit are shown in Fig. 5 as a black line and the fitted constants are shown in Table S17, Expt. #5 (ESI†). Under these high temperature conditions, 70% of the CH2OH growth occurs due to reactions of CH3O with the pH2 host. This is what we expect because the reaction of CH3O with the pH2 host does not rely on H atom diffusion, and thus it should still readily occur at 4.34 K. The remaining 30% of the CH2OH growth occurs with a rate constant of k2 = 1.2(8) × 10−2 min−1 and we will explore the interpretation of this result in the Discussion section. Note that the difference in the CH2OH post-photolysis growth at 4.3 K is also reflected in the kinetics of other species that rely on H atom quantum diffusion to occur.We then lowered the temperature of the sample to 1.74 K and mark the first data point recorded at the lower temperature with an arrow in Fig. 5. We let the sample equilibrate and recorded four repeated FTIR spectra. We did not detect any significant changes in the concentration of any of the species implying that significant concentrations of H atoms are not present in the sample at this time. After the sample equilibrated at the lower temperature (1.74(1) K), we photolyzed the sample for a second time (photo #2) and recorded the ensuing kinetics. Consistent with our previous low temperature experiments, we observe the complicated CH2OH growth kinetics that can be fit to the sum of three single exponential growth expressions. We find similar fitted parameters showing significant contributions to the growth of CH2OH from the slow k3 process. We also detect growth in the CHO concentration and decay in the CH3OH and CH2O concentrations that support our interpretation of the kinetics. We point out that for the two photolysis exposures at different temperatures, the amount of fast CH2OH growth and the fitted k1 rate constants are equal to within the fitted uncertainties. This supports our assignment of the fast process to reactions of the CH3O with the pH2 host. The photolysis conditions of both exposures are the same and therefore we produce comparable amounts of CH3O during photolysis that then decay at the same rate. We expect the rate constant for reaction of the CH3O photofragment with the pH2 host to be independent of temperature over this range because it does not depend on H atom diffusion. Basically, this rate constant characterizes the pseudo first-order decay kinetics ([pH2] ≫ [CH3O]) of CH3O in the pH2 host; the two reactive species are in constant physical contact because the CH3O is produced in solid pH2. In contrast, a reaction of an H atom with CH3OH requires these two species to be in close proximity and therefore depends on the details of H atom quantum diffusion. These results verify that H atom quantum diffusion is qualitatively different at these two temperatures and implies that only at the lower temperature does the H atom undergo long-range migration and reaction with CH3OH.
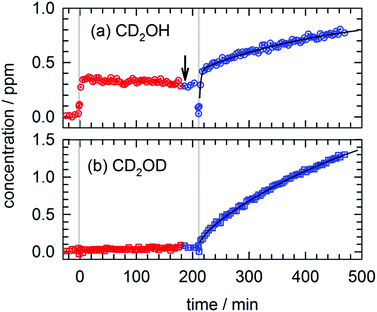
We performed a similar temperature dependent photolysis experiment on a CD3OD/pH2 sample. The full kinetic data for this experiment is shown in Fig. S9 in the ESI† and in Fig. 6 we show the results for just CD2OH and CD2OD. We deposit the CD3OD/pH2 sample, raise the temperature to 4.36 K, and record four FTIR spectra prior to photolysis. As can be seen in Fig. 6, photolysis at 4.36 K produces around 0.35 ppm of CD2OH and almost no CD2OD as expected based on the high temperature CH3OH/pH2 photolysis results. That is, CD2OH can still be produced by reactions of the CD3O photofragment with the pH2 host, but CD2OD cannot be produced by this mechanism. These findings are also consistent with the work of Lee and co-workers who did not report30 observation of the CD2OD isotopomer in their photolysis experiments conducted at 3.2 K. This isotopomer can only be produced by H atom reactions with CD3OD and these quantum diffusion limited reactions do not occur at higher temperatures (only at 1.8 K). Then the sample temperature is lowered (as marked with an arrow in Fig. 6) and after the sample equilibrates it is photolyzed for a second time. Photolysis at 1.67(1) K clearly shows the qualitatively different kinetics for CD2OH and CD2OD. The CD2OH shows significant contributions from two first-order processes with rate constants that match the previously recorded k1 and k3 rate constants. Note the CD2OD kinetics only show a minor medium rate constant component (∼4%) with greater than 96% coming from the slow k3 component. In this case, the different post-photolysis kinetics for CD2OH and CD2OD is even more evident than in Fig. 4. Furthermore, the different temperature behaviors of the CD2OD/CD2OH kinetic traces are consistent with the temperature dependence measured in the 193 nm photolysis of CH3OH/pH2. We note for completeness, that we performed another experiment on a CD3OD/pH2 sample where we conducted the temperature dependent photolysis in the reverse order (e.g., low and high) and rigorously found the same behavior (see Fig. S10 and Tables S18 and S19, ESI†).
4. Discussion
4.1 Understanding the CH2OH (CD2OH) growth kinetics
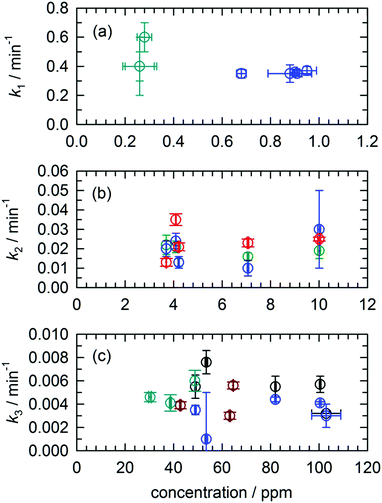
One of the features of the complex CH2OH (CD2OH) growth kinetics that initially confused us was why it separated into three distinct first-order processes. We show in Fig. 7 pseudo first-order plots of all the extracted rate constants based on the assigned reaction mechanisms. For example, for the CH3O + H2 reaction we plot in Fig. 7(a) the extracted k1 rate constant measured from the CH2OH growth curve as a function of the initial CH3O concentration (also estimated from the fit). Based on the assigned mechanism, the rate law for the production of CH2OH via the fast k1 reaction should be, Rate = k1[pH2][CH3O], but since the pH2 concentration is constant, it can be written in a pseudo first-order form as Rate = keff1[CH3O] where keff1 = k1[pH2]. As expected, the extracted rate constant shows no dependence on the initial CH3O concentration and gives a precise average rate constant of k1 = 0.36(1) min−1. The fact that this fast first-order process can be separated from the other two CH2OH growth processes immediately implies that the fast process is occurring by a different reaction mechanism than the other two. This is consistent with assigning this fast rate process of the CH2OH growth to reaction mechanism (2) that does not involve H atom reactants. Similarly, we extract a comparable fast rate constant (see Fig. 7(a)) from the CD2OH growth for a lower initial CD3O concentration consistent with the rate limited tunneling step being abstraction of an H atom from a nearby pH2 molecule.We can roughly estimate the timescale for the first tunneling reaction step as follows. If we model the reaction as tunneling through a square barrier, we can calculate the probability or rate constant (s−1) using the following expression,
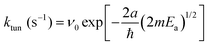 | (8) |
We assign both the medium (k2) and slow (k3) rate constants for CH2OH growth at low temperature to reactions with mobile H atoms. These H atom quantum diffusion reactions are different from reactions of a chemical species with the pH2 host because they require the H atoms to both quantum diffuse and react. The reason we can separate the fast growth of CH2OH from these other first-order growth processes is because the fast reaction is occurring by a different reaction mechanism than the H atom quantum diffusion reactions, i.e., reactions of CH3O with the pH2 host. However, why the medium and slow CH2OH growth processes can be separated into two different “types” of first-order H atom quantum diffusion reactions is not so immediately apparent. Assuming that all H atoms quantum diffuse at the same rate and react with different dopant species at different rates depending on the barrier to reaction, then you should only measure one effective rate constant that equals the sum of all the first-order rate constants. To better illustrate this idea examine Fig. 3. Only a small percentage (9.4%) of the H atoms react with a medium rate constant. The majority of H atoms (74.1%) react with a much slower rate constant. How can this be that the medium rate constant reaction does not use up all the H atom reactants? Clearly, H atom reactions with CH2O should continue to occur given that the CH2O concentration is still non-zero (see Fig. 2). But, indeed this is not what we observe. The ability to decompose these two CH2OH growth processes into two first-order reactions immediately suggests that there are different “types” of H atoms.
Another indication that quantum diffusion can be selective such that H atoms only diffuse next to certain species is given in the pseudo first-order rate constant plots shown in Fig. 7. For both the medium (k2) and slow rate (k3) coefficients that we have assigned to H atom reactions that involve quantum diffusion, we observe that the effective rate constant extracted from the fits does not scale linearly with the concentration of the H atom reaction partner. For example, take the reaction of H atoms with CH2O that produces CHO which are shown as green circles in Fig. 7(b). Given that this is an elementary step we can immediately write the rate law as Rate = k[CH2O][H]. Assuming that the CH2O concentration does not change much, we can rewrite the rate law as Rate = keff[H], where keff = k[CH2O]. This implies that the effective pseudo first-order rate constant keff should scale linearly with the CH2O concentration. Examination of Fig. 7(b) shows that this is not the case, instead, the measured k2 rate constant remains constant for changes in the initial CH2O concentration of more than a factor of 2 (e.g., 4 ppm to 10 ppm). We have now observed this behavior for a variety of H atom quantum diffusion reactions that we have studied to date.7,23 We observe the same behavior for the H + CH3OH → H2 + CH2OH reaction with the slowest rate constant where the measured rate constant does not scale linearly with the initial CH3OH concentration (see Fig. 7(c)). Further, we measure the same rate constant for the growth of CD2OD (brown circles) or CD2OH (cyan circles). We take this as evidence that the reaction is not “diffusion limited” in the normally defined sense. As we have shown previously for the H + NO reaction,23 because the H atom continues to be mobile due to quantum diffusion the bimolecular reaction kinetics are intrinsically first-order (the rate does not depend on the CH3OH concentration over the 75 to 120 ppm range) and the H atom decay kinetics reflect the H atom quantum diffusion rate, not the tunneling reaction rate of H atoms with CH3OH.
We speculate that the two different rates for the H atom quantum diffusion reactions are caused by both short- and long-range diffusion mechanisms. That is, the reactions that occur with a faster first-order time constant represent reactions of H atoms with other photofragment species that are nearby. Under these conditions where the CH3OH concentrations is the largest, but still rather dilute (<100 ppm), the dominant H atom decay channel is the reaction of H atoms with CH3OH. Only this reaction continues to occur over the full length of the experiment and constitutes proportionally the greatest amount of H atom decay. This implies that the H atom reactions with CH2O only occur for H atoms that are generated in near proximity to the CH2O photofragment. This explains why the amount of H atoms that decay via the medium rate (k2) tunneling reactions with CH2O is always small; only a subset of the generated H atoms is produced near another chemical impurity. In addition, these H atoms may be the result of secondary photolysis and be in regions of the crystal that are damaged or strained. One possible example is an H atom created in an interstitial site close to a CH2O photofragment. However, H atoms that quantum diffuse through the solid over longer distances only react with the CH3OH molecule. Thus, the two “types” of H atoms that are formed during the in situ CH3OH photolysis step are H atoms in close proximity to other photofragments, and well isolated H atoms. By well-isolated we mean H atoms produced in substitutional sites far removed from other chemical impurities. The smaller fraction of H atoms that react on a faster timescale do so because they have smaller distances to quantum diffuse and react. These short-range H atoms diffuse differently because the quantum diffusion is perturbed by the presence of a nearby chemical dopant or because the H atom is produced in a region that is strained. Once these H atoms are consumed, these reactions stop occurring and now the only H atom reactions possible involve long-range quantum diffusion through the pH2 solid and the reaction with CH3OH. Clearly this interpretation of the data is speculative and more experiments are needed to refine our understanding. However, two features measured in this study provide important clues as to the details of this chemistry. First, the H atom reactions do not obey pseudo first-order kinetics and second they can be separated into two different first-order processes.
4.2 Signatures of H atom quantum diffusion reactions
Another important signature of an H atom quantum diffusion reaction is that because the reaction kinetics reflects the H atom diffusion rate and not the tunneling reaction rate with specific chemical dopants, the H atoms do not necessarily decay by the tunneling reaction with the lowest reaction barrier. For example, Fig. 1(b) shows the reaction barriers for the three exothermic reactions of an H atom with CH2O. We assign the dominant H atom decay channel to the H + CH2O → CH2OH reaction which has the highest barrier. Now it could also be occurring via the reaction that produces the CH3O intermediate, but we also observe CHO growth that we assign to reactions of H + CH2O that has the intermediate barrier. This points to an important working hypothesis; the decay dynamics and kinetics are controlled by H atom quantum diffusion, not the individual reaction tunneling rates. This goes against conventional wisdom in low temperature tunneling reactions and is a ramification of the somewhat unique reaction conditions that exist in low temperature solid pH2 where the H atom continues to quantum diffuse even at the lowest temperatures. Take for example the lack of H atom reactions with CO that we observe under these conditions. This reaction has a very low barrier to reaction (Ea = 1590 ± 50 cm−1).66 This implies that the H atom has a much greater probability of diffusing next to a CH2O or CH3OH molecule compared to CO. The requirement that the two species diffuse next to each other restrains the chemistry that can occur. Quantum diffusion limited chemistry likely depends solely on the probability that the H atoms diffuse to a nearest neighbor site of a potential reactant. The presence and type of chemical impurity can also likely steer the trajectory of the incoming H atom such that the probability an H atom tunnels next to certain impurities is very low or high.Another important signature of H atom quantum diffusion limited chemistry is the strong temperature dependence these reactions show. The H atom decay channels and rates depend on the details of how an H atom diffuses next to a chemical impurity and this differs from the quantum diffusion rates in pure pH2. H atom quantum diffusion in a perfect pH2 crystal proceeds via a resonant tunneling mechanism H + H2 → H2 + H where the initial and final lattice positions of the H atom have exactly the same energy due to the translational symmetry of the crystal.16–18 The presence of crystal imperfections (e.g., chemical dopants) breaks this translational symmetry and causes a mismatch in the zero point energies of the H atom in for example second nearest and nearest neighbor lattice sites which greatly reduces the tunneling rate from the resonant value. This level mismatch can be compensated for by one- and two-phonon processes, which leads to a strong temperature dependence of the H atom quantum diffusion rate close to crystal imperfections.32 Not only is the rate changed, but the two different phonon assisted mechanisms lead to qualitatively different diffusion trajectories.32 For attraction between the reaction partners, diffusion towards the reaction partner is accompanied by spontaneous emission of phonons. The rate of spontaneous emission is proportional to ω3 (ω is the phonon emission frequency) and thus the most probable quantum diffusion jump is along the energy gradient (toward the chemical impurity).32 This mechanism would be operative only at the last stages of pairing when the intermolecular forces with the chemical dopant are the strongest. This mechanism is also independent of temperature. In contrast, the two-phonon mechanism where a thermal phonon inelastically scatters off the H atom–pH2 pair can either result in positive or negative energy mismatch jumps. Because it requires the presence of phonons, this mechanism becomes more important at higher temperatures. For the two-phonon mechanism, the most facile tunneling trajectory is along small energy mismatches.32 This mechanism therefore leads to H atom trajectories that avoid chemical dopants. This combination of resonant, one- and two-phonon mechanisms can lead to temperature dependent H atom quantum diffusion where the different diffusional mechanisms compete with each other. While the details of how H atom quantum diffusion towards chemical impurities still need to be worked out, this work and others from this laboratory6,7,23 show that H atom quantum diffusion reactions typically show a strong temperature dependence over the 1.7 to 4.3 K temperature range.
5. Summary
We show in this work that CH3OH is readily photodissociated in solid pH2 using 193 nm laser radiation. We identify CH2O and CO as the major photolysis products and that they are produced in comparable amounts under these conditions. Through detailed kinetic studies of the sample after photodissociation, we assert that CH3O is also produced during photolysis but can readily react via tunneling reactions with the pH2 host to ultimately produce CH2OH. While we do not observe the CH3O intermediate directly, the fast growth in the CH2OH concentration right after photolysis is assigned to CH3O reactions with the pH2 host. This mechanism is supported using similar photolysis studies of CD3OD where we demonstrate the kinetics of CD2OD and CD2OH are consistent with reactions with the pH2 host and not unimolecular isomerization (CH3O → CH2OH). Indeed, the measured fast CH2OH rate constant is also comparable to the literature value30 for the CH3O decay rate in solid pH2. This indicates that pH2 matrix isolation cannot be used to store the CH3O radical for long periods of time.One of the major experimental observations of this study is that the H + CH3OH → H2 + CH2OH reaction continues to occur long after the photolysis laser is shut off when the sample is maintained at 1.8 K. In fact, detailed analysis of the CH2OH growth kinetics after photolysis indicate that at least three separate tunneling reactions are contributing to the CH2OH growth; (i) the fast initial growth is due to reactions of the photoproduced CH3O with the pH2 host, (ii) the medium rate growth is due to H atom reactions with the CH2O photofragment that are likely produced in close proximity, and (iii) the slowest and largest contribution to the growth is due to long-range migration of H atoms and reaction with CH3OH. The different mechanisms of CH2OH growth are confirmed via simultaneous kinetic measurements on CH3OH and CH2O. The reason the tunneling reaction of CH3O with the pH2 host represents the fastest CH2OH growth mechanism is because the two reagents are in constant physical contact. Tunneling reactions of a photogenerated species with the pH2 host can be relatively improbable (have large reaction barriers), but still represent the fastest decay channel because the two species do not need to diffuse to come in contact with each other to react. In contrast, reactions between an H atom and another dopant species require the two species to be in neighboring lattice sites, and this relies strongly on the basic transport mechanism of the H atom. Therefore, typically H atom reactions with other dopants are much slower than reactions with the pH2 host and can be said to be quantum diffusion limited.
The second major finding of this work is that the H + CH3OH reaction shows anomalous temperature dependence. Namely, this reaction readily occurs at 1.8 K while at 4.3 K it does not. This is the third example measured in this laboratory of an H atom reaction in solid pH2 that more readily occurs at low temperature.6–8 As we discuss in this paper, we believe the anomalous temperature dependence is related to the details of H atom quantum diffusion. We show in this paper that the expected dependence on reaction partner concentration for the pseudo first-order H atom reaction kinetics is not observed implying that the rate limiting step is not diffusion limited in the normal sense. H atom quantum diffusion limited reactions in solid pH2 is still not fully understood and deserves further investigation. For example, not all H atom reactions with chemical dopants show this same anomalous temperature dependence. We note that the H + NO → HNO/NOH association reaction has a rate constant that increases with temperature over the 1.7 K to 4.3 K temperature range in an Arrhenius-type fashion, but yet also does not show pseudo-first order kinetics.23
Conflicts of interest
There are no conflicts to declare.Acknowledgements
We want to thank undergraduate Kylie A. Kufeld for conducting the first set of experiments in this project. The authors thank the National Science Foundation for its generous support through Grant CHE 08-48330 and CHE 13-62497.References
- Hydrogen Effects in Catalysis, ed. Z. Paál and P. G. Menon, Marcel Dekker, Inc., New York, 1988 Search PubMed.
- A. G. G. M. Tielens, The Physics and Chemistry of the Interstellar Medium, Cambridge University Press, Cambridge, 2005 Search PubMed.
- A. G. G. M. Tielens, Rev. Mod. Phys., 2013, 85, 1021 CrossRef CAS.
- T. Hama and N. Watanabe, Chem. Rev., 2013, 113, 8783 CrossRef CAS PubMed.
- M. Dincă and J. R. Long, Angew. Chem., Int. Ed., 2008, 47, 6766 CrossRef PubMed.
- F. M. Mutunga, S. E. Follett and D. T. Anderson, J. Chem. Phys., 2013, 139, 151104 CrossRef PubMed.
- L. O. Paulson, F. M. Mutunga and S. E. Follett, et al. , J. Phys. Chem. A, 2014, 118, 7640 CrossRef CAS PubMed.
- W. R. Wonderly and D. T. Anderson, J. Phys. Chem. A, 2014, 118, 7653 CrossRef CAS PubMed.
- Q. Cao, S. Berski and Z. Latajka, et al. , Phys. Chem. Chem. Phys., 2014, 16, 5993 RSC.
- T. Miyazaki, Atom Tunneling Phenomena in Physics, Chemistry and Biology, Springer-Verlag, Berlin, Heidelberg, New York, 2004 Search PubMed.
- T. Miyazaki, N. Iwata and K. P. Lee, et al. , J. Phys. Chem., 1989, 93, 3352 CrossRef CAS.
- T. Miyazaki, J. Kumagai and T. Kumada, Radiat. Phys. Chem., 2001, 60, 381 CrossRef CAS.
- T. Miyazaki, S. Mori and T. Nagasaka, et al. , J. Phys. Chem. A, 2000, 104, 9403 CrossRef CAS.
- T. Momose, M. Fushitani and H. Hoshina, Int. Rev. Phys. Chem., 2005, 24, 533 CrossRef CAS.
- M. Fushitani and T. Momose, Low Temp. Phys., 2003, 29, 740 CrossRef CAS.
- T. Kumada, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 68, 052301 CrossRef.
- T. Kumada, S. Mori and T. Nagasaka, et al. , J. Low Temp. Phys., 2001, 122, 265 CrossRef CAS.
- T. Kumada, M. Sakakibara and T. Nagasaka, et al. , J. Chem. Phys., 2002, 116, 1109 CrossRef CAS.
- K. Yoshioka, P. L. Raston and D. T. Anderson, Int. Rev. Phys. Chem., 2006, 25, 469 CrossRef CAS.
- K. A. Peterson, D. E. Woon and T. H. Dunning, Jr., J. Chem. Phys., 1994, 100, 7410 CrossRef CAS.
- L. J. Lauhon and W. Ho, Phys. Rev. Lett., 2000, 85, 4566 CrossRef CAS PubMed.
- K. Kuwahata, T. Hama and A. Kouchi, et al. , Phys. Rev. Lett., 2015, 115, 133201 CrossRef CAS PubMed.
- M. Ruzi and D. T. Anderson, J. Phys. Chem. A, 2015, 119, 12270 CrossRef CAS PubMed.
- H. Linnartz, S. Ioppolo and G. Fedoseev, Int. Rev. Phys. Chem., 2015, 34, 205 CrossRef CAS.
- S. Satyapal, J. Park and R. Bersohn, J. Chem. Phys., 1989, 91, 6873 CrossRef CAS.
- Y. Wen, J. Segall and M. Dulligan, et al. , J. Chem. Phys., 1994, 101, 5665 CrossRef CAS.
- F. M. Mutunga and D. T. Anderson, J. Phys. Chem. A, 2015, 119, 2420 CrossRef CAS PubMed.
- E. F. V. Carvalho, A. N. Barauna and F. B. C. Machado, et al. , Chem. Phys. Lett., 2008, 463, 33 CrossRef CAS.
- Y.-F. Lee, L.-J. Kong and Y.-P. Lee, J. Chem. Phys., 2012, 136, 124510 CrossRef PubMed.
- Y.-F. Lee, W.-T. Chou and B. A. Johnson, et al. , J. Mol. Spectrosc., 2015, 310, 57 CrossRef CAS.
- G. Lendvay, T. Bérces and F. Márta, J. Phys. Chem. A, 1997, 101, 1588 CrossRef CAS.
- A. E. Meyerovich, Phys. Rev. B: Condens. Matter Mater. Phys., 1990, 42, 6068 CrossRef CAS.
- M. Tammaro, M. P. Nightingale and A. E. Meyerovich, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 2573 CrossRef CAS.
- Y. Kagan and L. A. Maksimov, Phys. Lett. A, 1983, 95, 242 CrossRef.
- L. O. Paulson and D. T. Anderson, J. Phys. Chem. A, 2009, 113, 1770 CrossRef CAS PubMed.
- M. E. Fajardo, in Physics and Chemistry at Low Temperatures, ed. L. Khriachtchev, Pan Stanford Publishing, Singapore, 2011, p. 167 Search PubMed.
- S. Tam and M. E. Fajardo, Rev. Sci. Instrum., 1999, 70, 1926 CrossRef CAS.
- S. Tam and M. E. Fajardo, Appl. Spectrosc., 2001, 55, 1634 CrossRef CAS.
- I. F. Silvera, Rev. Mod. Phys., 1980, 52, 393 CrossRef CAS.
- M. J. Frisch, G. W. Trucks and H. B. Schlegel, et al., Gaussian 09, Revision A.02, Gaussian, Inc., Wallingford, CT, 2009 Search PubMed.
- T. H. Dunning, Jr., J. Chem. Phys., 1989, 90, 1007 CrossRef.
- D. E. Woon and T. H. Dunning, Jr., J. Chem. Phys., 1993, 98, 1358 CrossRef CAS.
- Y.-P. Lee, Y.-J. Wu and R. M. Lees, et al. , Science, 2006, 311, 365 CrossRef CAS PubMed.
- M. E. Fajardo, C. M. Lindsay and T. Momose, J. Chem. Phys., 2009, 130, 244508 CrossRef PubMed.
- M. E. Fajardo, J. Phys. Chem. A, 2013, 117, 13504 CrossRef CAS PubMed.
- L. Feng, J. Wei and H. Reisler, J. Phys. Chem. A, 2004, 108, 7903 CrossRef CAS.
- M. A. Roberts, E. N. Sharp-Williams and D. J. Nesbitt, J. Phys. Chem. A, 2013, 117, 7042 CrossRef CAS PubMed.
- M. E. Jacox and D. E. Milligan, J. Mol. Spectrosc., 1973, 47, 148 CrossRef CAS.
- M. E. Jacox, Chem. Phys., 1981, 59, 213 CrossRef CAS.
- B.-M. Cheng, M. Bahou and W.-C. Chen, et al. , J. Chem. Phys., 2002, 117, 1633 CrossRef CAS.
- P. L. Raston, S. C. Kettwich and D. T. Anderson, Low Temp. Phys., 2010, 36, 495 CrossRef.
- K. A. Kufeld, W. R. Wonderly and L. O. Paulson, et al. , J. Phys. Chem. Lett., 2012, 3, 342 CrossRef CAS PubMed.
- W. R. Wonderly and D. T. Anderson, Low Temp. Phys., 2012, 38, 853 CrossRef.
- M. E. Fajardo, S. Tam and M. E. DeRose, J. Mol. Struct., 2004, 695, 111 CrossRef.
- D. E. Woon, Astrophys. J., 2002, 569, 541 CrossRef CAS.
- E. Kamarchik, C. Rodringo and J. M. Bowman, et al. , J. Chem. Phys., 2012, 136, 084304 CrossRef CAS PubMed.
- C. Pirim, L. Krim and C. Laffon, et al. , J. Phys. Chem. A, 2010, 114, 3320 CrossRef CAS PubMed.
- C. Pirim and L. Krim, Phys. Chem. Chem. Phys., 2011, 13, 19454 RSC.
- C. Pirim and L. Krim, Chem. Phys., 2011, 380, 67 CrossRef CAS.
- C. Pirim and L. Krim, RSC Adv., 2014, 4, 15419 RSC.
- B. Kerkeni and D. C. Clary, J. Chem. Phys., 2004, 121, 6809 CrossRef CAS PubMed.
- R. Meana-Paneda, D. G. Truhlar and A. Fernandez-Ramos, J. Chem. Phys., 2011, 134, 094302 CrossRef PubMed.
- A. Serrallach, R. Meyer and H. H. Günthard, J. Mol. Spectrosc., 1974, 52, 94 CrossRef.
- R. Wugt Larsen, P. Zielke and M. A. Suhm, J. Chem. Phys., 2007, 126, 194307 CrossRef PubMed.
- M. Ruzi and D. T. Anderson, J. Phys. Chem. A, 2013, 117, 13832 CrossRef CAS PubMed.
- P. S. Peters, D. Duflot and L. Wiesenfeld, et al. , J. Chem. Phys., 2013, 139, 164310 CrossRef PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c7cp05064j |
| This journal is © the Owner Societies 2018 |