Multicomponent ionic liquid CMC prediction†
Abstract
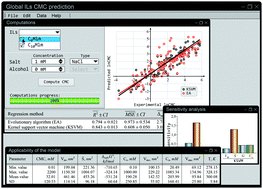
We created a model to predict CMC of ILs based on 704 experimental values published in 43 publications since 2000. Our model was able to predict CMC of variety of ILs in binary or ternary system in a presence of salt or alcohol. The molecular volume of IL (Vm), solvent-accessible surface (Ŝ), solvation enthalpy (ΔsolvG∞), concentration of salt (Cs) or alcohol (Ca) and their molecular volumes (Vms and Vma, respectively) were chosen as descriptors, and Kernel Support Vector Machine (KSVM) and Evolutionary Algorithm (EA) as regression methodologies to create the models. Data was split into training and validation set (80/20) and subjected to bootstrap aggregation. KSVM provided better fit with average R2 of 0.843, and MSE of 0.608, whereas EA resulted in R2 of 0.794 and MSE of 0.973. From the sensitivity analysis it was shown that Vm and Ŝ have the highest impact on ILs micellization in both binary and ternary systems, however surprisingly in the presence of alcohol the Vm becomes insignificant/irrelevant. Micelle stabilizing or destabilizing influence of the descriptors depends upon the additives. Previous attempts at modelling the CMC of ILs was generally limited to small number of ILs in simplified (binary) systems. We however showed successful prediction of the CMC over a range of different systems (binary and ternary).
- This article is part of the themed collection: 2017 PCCP HOT Articles


 Please wait while we load your content...
Please wait while we load your content...