Intriguing transport dynamics of ethylammonium nitrate–acetonitrile binary mixtures arising from nano-inhomogeneity

Abstract

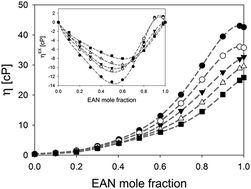
Binary mixtures of ethylammonium nitrate and acetonitrile show interesting properties that originate from the structural and dynamical nano-heterogeneity present in ionic liquids. These effects are most pronounced when the ionic liquid is the minority compound. In this study the transport properties of such mixtures are studied, including viscosity, self-diffusion and conductivity. The results strongly support the presence of structural inhomogeneity and show an interesting composition-dependent behaviour in the mixtures.