Polaron formation mechanisms in conjugated polymers
Joel H.
Bombile
 ,
Michael J.
Janik
and
Scott T.
Milner
*
,
Michael J.
Janik
and
Scott T.
Milner
*
Pennsylvania State University, University Park, PA 16802, USA. E-mail: stm9@psu.edu; Fax: +1 (814) 865 7846; Tel: +1 (814) 863 9355
First published on 5th December 2017
Abstract
In semiconducting polymers, interactions with conformational degrees of freedom can localize charge carriers, and strongly affect charge transport. Polarons can form when charges induce deformations of the surrounding medium, including local vibrational modes or dielectric polarization. These deformations then interact attractively with the charge, tending to localize it. First we investigate vibrational polaron formation in poly(3-hexylthiophene) [P3HT], with a tight-binding model for charges hopping between adjacent rings, coupled to ring distortions. We use density functional theory (DFT) calculations to determine coupling constants, including the “spring constant” for ring distortions and the coupling to the charge carrier. On single chains, we find only broad, weakly bound polarons by this mechanism. In 2d crystalline layers of P3HT, even weak transverse hopping between chains destabilizes this polaron. Then, we consider polarons stabilized by dielectric polarization, described semiclassically with a polarizable continuum interacting with the carrier wavefunction. In contrast to vibrational polarons, we find dielectrically stabilized polarons in P3HT are narrower, more strongly bound, and stable in 2d crystalline layers.
1 Introduction
Organic semiconductors uniquely combine useful electronic properties with mechanical flexibility, low cost, and solution processing. These materials can serve as active elements in electronic devices such as field effect transistors,1 light-emitting diodes,2 and solar cells.3 Organic semiconductors are based on either conjugated polymers or small molecules. Of these two classes, polymers are more studied because they are easier to process and have better mechanical properties.Conjugated polymer chains have valence and conduction bands with extended states that can conduct current. However, polymers are soft, and have many accessible deformation modes. Charge carriers in semiconducting polymers can interact with material deformations in two ways. First, a charge can induce the material to deform locally, either conformationally or electronically. The deformation may in turn attract and stabilize the charge in a particular location, forming a polaron, as first described by Landau.4 Second, a charge can interact with quenched structural disorder, which presents a random potential. The random potential tends to localize the charge, particularly in low-dimensional conductors, as described by Anderson.5 Localization effects are particularly strong near the band edges,6,7 affecting electronic transport,8 light absorption and emission,9 and other electronic and optical properties.
Among the many conformational degrees of freedom available to semiconducting polymers, the most important for potentially localizing charges is variations in the dihedral angle. When the dihedral angle between successive monomers is rotated away from the trans configuration, conjugation along the chain is progressively broken, which inhibits charge hopping between monomers. Dihedral disorder is particularly important for amorphous melts or single chains in solution, where no crystalline order exists to keep the chains in the trans state. Dihedral disorder has strong effects on opto-electronic properties,10–14 and is effective in localizing charge carriers.6,8
Local vibrational modes can also interact with charges on the chain. In conventional crystalline semiconductors these modes are described as phonons, coupled to charges by the electron–phonon coupling. In molecules, these local modes respond to the presence of a charge on a monomer, distorting the monomer shape and lowering the total energy. In turn, the charge is attracted to the distorted monomer. If the deformation mode is soft enough and the coupling to the charge strong enough, this mechanism can localize the charge along the chain, forming a polaron.
Polarons in 1-dimensional systems such as conjugated polymers can be represented with the Holstein model.15,16 In this model, a charge carrier on a linear array of sites is treated within the tight binding approximation, and coupled to a single harmonic oscillator on each site representing a local vibrational mode.17–22
The effect of dihedral disorder has also been studied with a disordered Holstein model, in which the hopping matrix elements are assumed to be random, with a phenomenological Gaussian distribution.18–20 More physically, the dihedral potential of most conjugated polymers is not harmonic, but rather is soft enough that large deviations from the most stable value are frequent at ambient temperature. The distribution of hopping matrix elements actually arises from the distribution of dihedral angles, though this link is obscured if an arbitrary variance is used as a model parameter. In recent work, this link is made explicit by obtaining the dihedral distribution from classical molecular dynamic simulations, and assuming a cosine dependence of hopping matrix element on dihedral angle, which works well for P3HT.23
In our previous paper6 examining poly(3-hexylthiophene) (P3HT), we described a charge carrier in a P3HT chain using a tight-binding model, in which the hopping of electron or holes are coupled to dihedral angle rotations. We used density functional theory (DFT) to compute how the hopping matrix element between successive rings varies with dihedral angle. We used the dihedral effective potential obtained from classical molecular dynamics (MD) simulations to quickly generate representative dihedrals, so that we could average tight-binding model predictions over chain conformations. In this way, our model predicted how dihedral disorder localizes the valence and conduction states, which ultimately broadens the UV-vis absorption edge.
In this paper, we extend our tight-binding model to consider polarons, both on single P3HT chains and in the two-dimensional layers within crystalline P3HT. Polarons can be stabilized by coupling to different deformations of the surrounding medium. Here, we consider two main couplings of the charge to the medium: local distortion of monomers in response to the presence of an electron or hole, and polarization of the surrounding dielectric. We will consider both, and determine their relative importance by comparing the resulting polaron size and binding energy from each mechanism.
To investigate monomer distortion as a mechanism to stabilize polarons, we use DFT to quantify the coupling between local vibrational modes on a monomer and an extra electron or hole. To describe polarons, the resulting Holstein Hamiltonian can be minimized with respect to the carrier wavefunction and mode amplitudes on each monomer.
Vibrational polarons on single P3HT chains with couplings computed using DFT were previously studied by Meisel and coworkers.17 They wrote a Holstein model in which holes and electrons couple to normal modes of thiophene rings along the chain, and used DFT to compute the coupling constants for all the local vibrational modes. Here we show this approach is equivalent to a simpler Hamiltonian with the charge carrier coupled to a single composite mode, which is simply the distortion a ring undergoes when a charge is present. Coupling constants can be computed for this composite mode without expanding in normal modes.
We use this Hamiltonian to investigate “ring polarons” (polarons stabilized by ring distortions), on both single chains and in two-dimensional crystalline layers. In these layers a small but non-vanishing transverse hopping matrix element couples adjacent monomers on neighboring chains. It turns out even a small transverse coupling can destabilize the single-chain ring polaron, which we demonstrate with scaling arguments and explicit calculations.
Polarons can also be stabilized by attractive electrostatic interactions of a charge carrier with the dielectric polarization it induces in the surrounding material. This polarization can arise either from displacement of partial charges in a polar medium, or from electronic polarization more generally. For P3HT crystals, we estimate and compare the polarizabilities arising from motion of partial charges and from electronic polarization, to find out which is the dominant contributor. We then describe a dielectrically stabilized polaron by treating the polarizable medium as a classical continuum interacting electrostatically with a localized carrier wavefunction.
To assess the most important contributors to polaron formation, we compare the characteristic lengths and binding energies among the different mechanisms treated individually. For comparison with dihedral disorder-induced localization in an amorphous P3HT melt, we apply our previous work6 to compute the size distribution of localized states, averaging over many chain conformations.
The paper is organized as follows. First we describe the tight-binding model for a charge carrier on a polymer chain, and its generalization to include coupling to ring distortions. Next, we use DFT to obtain the two new model parameters, namely the “spring constant” for ring distortions, and the coupling between ring distortions and the carrier. We compute the single-chain ring polaron, first using a trial Gaussian wavefunction, and then by minimizing over the wavefunction on each ring. We generalize the single-chain ring polaron to a 2d P3HT crystalline layer, and find conditions at which transverse hopping between chains renders such a polaron unstable. Then, we consider dielectric stabilization of polarons in P3HT. We compare contributions to dielectric polarization from reorientation of dipoles on thiophene rings, with electronic polarization arising throughout the medium. We then present a semiclassical model of dielectric polarons, in which the polarizable medium is treated as a classical continuum, interacting with the carrier wavefunction. We compare the relative importance of different polaron mechanisms, and assess polaronic contributions to effective mass and carrier damping. Finally, we compare typical polaron length scales to disorder-induced localized states in amorphous P3HT.
2 Tight binding model
We use a tight-binding model to describe a charge carrier on a P3HT chain. In the model, a charge carrier occupies sites with some onsite energy, and is stabilized by hopping between neighboring sites. The polymer chain is modeled as a one-dimensional array of sites, each site corresponding to a backbone moiety (for P3HT, a thiophene ring). The Hamiltonian is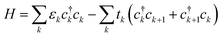 | (1) |
The onsite energies and hopping matrix elements are sensitive to conformational changes. The hopping matrix elements vary strongly with dihedral angle. In previous work6 we determined how tk depends on the dihedral angle between rings, by matching the band structure computed within the tight-binding model to DFT results. The hopping matrix elements fall to zero as the dihedral angle approaches 90°, which breaks conjugation between adjacent rings.
The onsite energies εk vary when the backbone moieties change shape, or when the surrounding medium becomes polarized. Both perturbations can occur in response to the presence of a charge carrier, and in turn can stabilize the localized charge, forming a polaron. We describe each mechanism in detail below.
3 Single-chain ring polaron
In P3HT chains, the backbone moieties are thiophene rings, which have many normal modes of deformation. To investigate the interaction of local deformation modes with charges on the rings, we write a Holstein model. Here the charge carrier is represented quantum-mechanically with a tight-binding model, while the ring normal modes are described as classical harmonic oscillators.The Hamiltonian takes the form
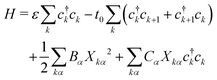 | (2) |
In writing eqn (2), we have assumed the modes on each ring are independent, neglecting any coupling that would lead to extended phonons along the chain. We have checked this approximation by using DFT to compute the difference in deformation energy between in-phase and out-of-phase deformations on alternating rings of a periodic chain. These deformations correspond to phonons at q = 0 and the band edge respectively, and have identical energies to within 2.5 percent, which indicates a very flat phonon band with nearly independent modes on each ring.
We determine the polaron ground state by minimizing the expectation value of the Hamiltonian with respect to the ring distortion amplitudes, and with respect to the carrier wave function. We write the wavefunction in terms of amplitudes ak on each site, as
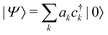 | (3) |
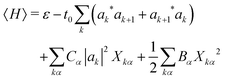 | (4) |
The mode amplitudes can be thought of as adjusting to whatever fractional charge is present. Minimizing with respect to the set of {Xkα} gives the result Xkα* = −(Cα/Bα)|ak|2. This immediately suggests a simplified model with only one composite mode on each ring, in which all the mode amplitudes Xkα on a site k are proportional to a single amplitude Xk: Xkα = (Cα/Bα)Xk. Substituting this form into the energy (4) gives
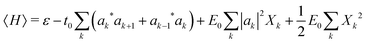 | (5) |
Here we have defined a characteristic energy 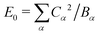 . Indeed, we could have started with a Hamiltonian in which the carrier is coupled on each ring to a single composite mode, which physically is just the deformation vector actually induced by a charge. For this single composite mode, the effective spring constant and coupling constant are
. Indeed, we could have started with a Hamiltonian in which the carrier is coupled on each ring to a single composite mode, which physically is just the deformation vector actually induced by a charge. For this single composite mode, the effective spring constant and coupling constant are ![[B with combining macron]](https://www.rsc.org/images/entities/i_char_0042_0304.gif) and
and ![[C with combining macron]](https://www.rsc.org/images/entities/i_char_0043_0304.gif) , and E0 equals
, and E0 equals ![[C with combining macron]](https://www.rsc.org/images/entities/i_char_0043_0304.gif) 2/
2/![[B with combining macron]](https://www.rsc.org/images/entities/i_char_0042_0304.gif) . (In the Appendix, we relate the composite mode explicitly to a normal mode expansion.)
. (In the Appendix, we relate the composite mode explicitly to a normal mode expansion.)
The polaron energy at the optimal composite mode amplitude Xk* = −|ak|2 is
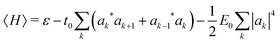 | (6) |
Characterization of the single mode
In our previous work,6 we determined the value of the hopping matrix element for electrons (t0 = 0.76 eV) and holes (t0 = 0.98 eV) using DFT. Here, we also use DFT to determine the composite eigenvector and the reorganization energy E0 for the single mode. To do this, we first compute the optimized geometries of periodic chains with and without a constant excess charge per monomer. We then compare the total energies of both charged and neutral chains, in both optimized geometries.We can define unit amplitude of deformation modes in many ways. A convenient choice for the single composite mode is to define X so the distortion in response to a fractional charge |ψ|2 is just X = |ψ|2. (This linear dependence of mode amplitude on fractional charge is implied by the form of the couplings, but can break down for large fractional charge because of nonlinear effects.) For this choice we evidently have E0 = ![[B with combining macron]](https://www.rsc.org/images/entities/i_char_0042_0304.gif) = −
= −![[C with combining macron]](https://www.rsc.org/images/entities/i_char_0043_0304.gif) . The energy per ring for constant charge per ring |ψ|2 is then
. The energy per ring for constant charge per ring |ψ|2 is then
| E(|ψ|2,X) = (ε − 2t0)|ψ|2 + E0((1/2)X2 − X|ψ|2) | (7) |
We can use DFT to find the composite mode induced on a ring by a unit charge, by comparing the optimized structure for a charged monomer with that of a neutral monomer.
We can then compute the reorganization energy in two ways. From eqn (7), we see that the energy increase to deform the neutral monomer into the same configuration as a partially charged monomer naturally adopts the form:
| ΔEn→c(X) = E(0,X) − E(0,0) = (1/2)E0X2 | (8) |
| ΔEc→n(|ψ|2) = E(|ψ|2,0) − E(|ψ|2,X(|ψ|2)) = (1/2)E0|ψ|2 | (9) |
As remarked above, we expect that the simple bilinear coupling and quadratic elastic constant terms will eventually be modified by nonlinear effects, for large enough charge per ring and mode amplitude. We can check for this explicitly by plotting ΔE(X) versus X, for which we expect a parabola (1/2)E0X2 at small X.
We can likewise check for nonlinear effects on the bilinear coupling term −E0X|ψ|2. The bilinear coupling term can be isolated by computing the difference in stabilization energy for a charged and neutral system, deformed with the same composite amplitude X:
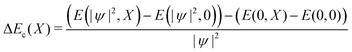 | (10) |
We perform all DFT calculations with the Vienna Ab initio Simulation Package (VASP), which uses plane wave basis sets and periodic boundary conditions to model periodic structures. Infinite polymer chains are 1-dimensional structures with a unit cell of one or more monomers. In VASP calculations, polymer chains with excess charge per ring automatically have a cancelling uniform background charge. No correction for this is necessary since our calculations only involve energy differences for structures with the same excess charge. All calculations were performed using the Perdew–Wang 1991 (PW91) generalized gradient approximation (GGA) functional, a basis set cutoff energy of 450 eV, the projector augmented wave approach for the ionic core interactions, and a k-point sampling of 7 × 1 × 1.
We use a unit cell of two rings, which is the smallest repeating cell for a chain in the all-trans configuration, in which the sulfur atoms alternately point “up” and “down” (see Fig. 1). (The total energy computed for the unit cell was divided by two to obtain the energy per ring.)
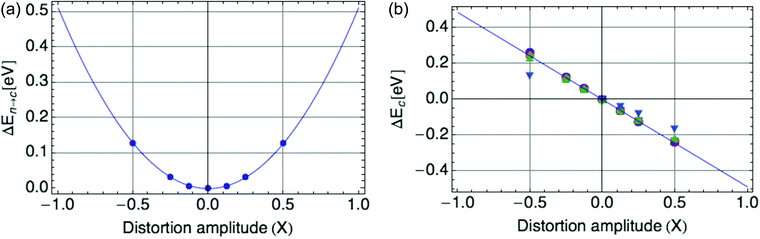
Fig. 2a displays the reorganization energy ΔEn→c(X) versus composite mode amplitude X, with a harmonic potential fitted to the small-amplitude data (below |X| = 0.5), with curvature E0 = ![[B with combining macron]](https://www.rsc.org/images/entities/i_char_0042_0304.gif) = 0.66 eV.
= 0.66 eV.
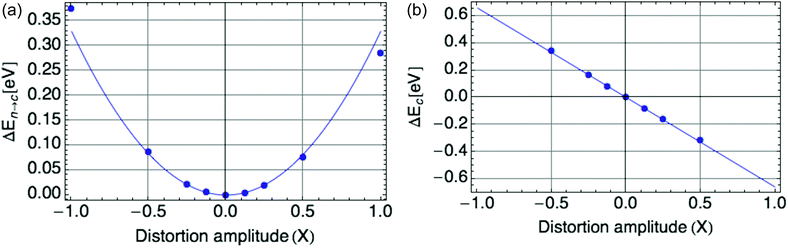 | ||
| Fig. 2 (a) Harmonic potential of single mode, with stiffness E0 = 0.66 eV. X is defined such that X = |ψ|2. (b) Coupling of single mode with hole, a value of E0 = −0.66 eV is shown. | ||
Fig. 2b displays the coupling term ΔEc(X) versus X, in which the mode amplitude X was varied from −0.5 to 0.5. We infer the coupling constant ![[C with combining macron]](https://www.rsc.org/images/entities/i_char_0043_0304.gif) = −E0 = −0.66 eV from the slope of the line fit to the DFT data. A low carrier density per ring of 0.25 was used, since at high onsite carrier density (near 1), the coupling term of eqn (2) deviates from linearity with |ψ|2 (see Fig. 9b in the Appendix section). These values of
= −E0 = −0.66 eV from the slope of the line fit to the DFT data. A low carrier density per ring of 0.25 was used, since at high onsite carrier density (near 1), the coupling term of eqn (2) deviates from linearity with |ψ|2 (see Fig. 9b in the Appendix section). These values of ![[C with combining macron]](https://www.rsc.org/images/entities/i_char_0043_0304.gif) and
and ![[B with combining macron]](https://www.rsc.org/images/entities/i_char_0042_0304.gif) confirm the expected equalities E0 =
confirm the expected equalities E0 = ![[B with combining macron]](https://www.rsc.org/images/entities/i_char_0042_0304.gif) = −
= −![[C with combining macron]](https://www.rsc.org/images/entities/i_char_0043_0304.gif) = 0.66 eV.
= 0.66 eV.
Ring polaron ground state
Having minimized the energy over mode amplitudes, to compute the polaron ground state we now minimize with respect to the carrier wavefunction. We can either impose a variational trial wavefunction and minimize with respect to its parameters, or brute-force minimize the energy with respect to the carrier amplitudes {ak} on every site.Since we expect a polaron to be localized, a normalized Gaussian with variable width σ is a reasonable trial wavefunction. We write the amplitudes {ak} as
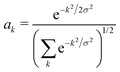 | (11) |
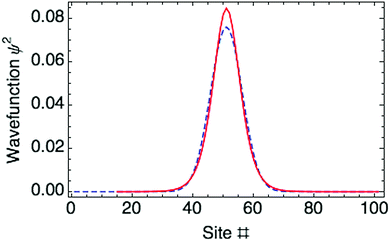
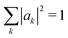 . Fig. 3 shows both approaches predict essentially the same polaron wave function.
. Fig. 3 shows both approaches predict essentially the same polaron wave function.
The optimized ring polaron has a width of 10 thiophene rings, defined by twice the standard deviation (SD) of the Gaussian carrier probability distribution. This is in good agreement with previous work of Meisel and coworkers.17
The polaron binding energy is the energy difference between the carrier extended state (with no reorganization of the medium) and the polaron state. The binding energy for the ring polaron on a P3HT chain is only 10 meV, much smaller than the thermal energy kT at room temperature (about 25 meV). Such a small binding energy will be easily overcome by the excess thermal energy, resulting in no ring polaron feature being observed. As such, this mechanism for polaron formation does not play an important role in charge transport at room temperature along P3HT chains.
Our analysis of polarons for hole carriers in the P3HT valence band is equally valid for electrons in the conduction band. The restructuring of rings due to an electron is geometrically different from the restructuring for a hole, but the characteristic energy E0 associated with this restructuring is the same, E0 = 0.66 eV. The electron ring polaron is about 8 rings wide, with a binding energy of 12 meV. The smaller size and larger binding energy result from a smaller hopping matrix element for electrons (t0 = 0.76 eV) versus holes (t0 = 0.98 eV).
Finally, we compare our results for polaron size to predictions from ab initio methods, which have their own challenges in describing polarons. Methods like Hartree–Fock (HF) and post-HF methods such as MP2 with their known over localization tendencies predict a polaron localized over just 4 rings27 (at half carrier maximum density). Pure DFT calculations show no localization of an excess charge; hybrid DFT with the functional BH and HLYP does capture polaron formation, though it retains the over-localization tendency of HF.27–29
Scaling argument for single-chain ring polaron
Our calculations are consistent with scaling arguments that predict how the polaron size and binding energy vary with the hopping matrix element t and reorganization energy E0. Scaling arguments are useful to estimate the strength of polaronic effects for polymers other than P3HT. As eqn (6) shows, polaron formation is governed by a balance between carrier kinetic energy and reorganization energy. The kinetic energy favors an extended carrier while the reorganization energy favors a more localized carrier; an optimal size results.The tight binding kinetic energy in eqn (1) is not obviously equivalent to the usual square gradient expression 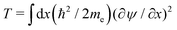 . To show the tight binding kinetic energy leads to a discretized square gradient term, we evaluate its expectation value in a single-particle state eqn (3), to obtain
. To show the tight binding kinetic energy leads to a discretized square gradient term, we evaluate its expectation value in a single-particle state eqn (3), to obtain
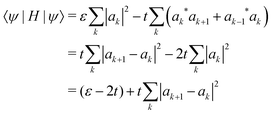 | (12) |
To see how the polaron scales with t and E0, consider a polaron of width L, encompassing N = L/Δ sites. The normalized wavefunction is then of order 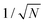 over N sites, and the kinetic energy scales as t/N2. The ring modes on each of the N sites have amplitudes of order E0|ψ|2 = E0/N; this leads to a stabilization energy per site of −E0/N2, for a total of −E0/N overall. The kinetic and stabilization energies scale differently with size so an optimum size results, at which the kinetic and stabilization energies are comparable. The optimum polaron size N* is of order t/E0, with a binding energy of order E02/t. Numerical calculations of the polaron size and binding energy for different values of E0/t satisfy these scaling relations exactly.
over N sites, and the kinetic energy scales as t/N2. The ring modes on each of the N sites have amplitudes of order E0|ψ|2 = E0/N; this leads to a stabilization energy per site of −E0/N2, for a total of −E0/N overall. The kinetic and stabilization energies scale differently with size so an optimum size results, at which the kinetic and stabilization energies are comparable. The optimum polaron size N* is of order t/E0, with a binding energy of order E02/t. Numerical calculations of the polaron size and binding energy for different values of E0/t satisfy these scaling relations exactly.
4 Ring polaron in a crystalline lamella
A P3HT crystal consists of lamellae of parallel thiophene chains, separated by layers containing the alkyl sidechains. There is practically no conduction through the insulating sidechain layers. Conduction occurs along the chain through the conjugated π-bonds, and between chain through the overlapping π-electron clouds of adjacent rings. Essentially, there is 2-dimensional charge transport within the lamellae, with charge carriers able to hop from ring to ring along and between chains.Charge carriers within a lamella can be described by a tight binding model, with a 2d array of sites corresponding to the thiophene rings. The 2d model extends the single chain Hamiltonian by adding hopping terms between rings on adjacent chains:
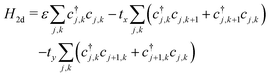 | (13) |
The 2d tight binding Hamiltonian is the starting point for investigating the stability of vibrational or “ring” polarons in crystalline P3HT. Like the single-chain case, polarons may in principle be stabilized by distortions of monomers on which charge resides. Following the same procedure as for the single-chain calculations, we add elastic and coupling terms for a single composite mode on each ring, and then minimize with respect to the mode amplitude on each ring in response to the carrier wavefunction amplitude.
The resulting energy takes the form
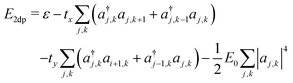 | (14) |
Scaling arguments for 2d ring polaron
In crystalline P3HT lamellae, the hopping matrix element is much smaller between chains than along chains. One might imagine that if the transverse hopping matrix element is very weak, we should continue to find an essentially 1d polaron along a single chain, with very small “leakage” of the wavefunction to adjacent chains. However, when we extend the scaling arguments of 1d polarons to 2d polarons, we find a surprising result.Suppose we have a hopping matrix elements tx and ty (with ty ≪ tx), and a polaron width of Nx in the x direction and Ny in the y direction. The normalized wavefunction is now of order 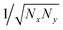 , over a total of NxNy sites. The kinetic energy, described by the square gradient terms, now scales as tx/Nx2 + ty/Ny2. The stabilization energy scales as −E0/(NxNy), since there are NxNy total sites with appreciable ring stabilization, and the wavefunction is of order 1/NxNy on these sites.
, over a total of NxNy sites. The kinetic energy, described by the square gradient terms, now scales as tx/Nx2 + ty/Ny2. The stabilization energy scales as −E0/(NxNy), since there are NxNy total sites with appreciable ring stabilization, and the wavefunction is of order 1/NxNy on these sites.
To simplify the scaling, we restore isotropy by defining Ny2 = (ty/tx)![[N with combining macron]](https://www.rsc.org/images/entities/i_char_004e_0304.gif) y2; now the gradient term is isotropic, of order tx(1/Nx2 + 1/
y2; now the gradient term is isotropic, of order tx(1/Nx2 + 1/![[N with combining macron]](https://www.rsc.org/images/entities/i_char_004e_0304.gif) y2), and the stabilization term scales as
y2), and the stabilization term scales as 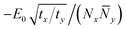 . By symmetry, we expect Nx and
. By symmetry, we expect Nx and ![[N with combining macron]](https://www.rsc.org/images/entities/i_char_004e_0304.gif) y are the same order. But now we have a surprise: the kinetic and binding energy terms scale the same way with Nx and
y are the same order. But now we have a surprise: the kinetic and binding energy terms scale the same way with Nx and ![[N with combining macron]](https://www.rsc.org/images/entities/i_char_004e_0304.gif) y, so there is no obvious minimum. For insight into what has changed in going from 1d to 2d, we proceed with numerical calculations for the polaron ground state.
y, so there is no obvious minimum. For insight into what has changed in going from 1d to 2d, we proceed with numerical calculations for the polaron ground state.
2d ring polaron ground state
The scaling argument suggests there may be no stable 2d ring polaron; its stability with respect to a free carrier must then depend on the characteristic energies tx, ty, and E0. The polaron binding energy is the energy difference between the polaron and a free carrier, given by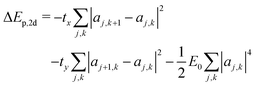 | (15) |
As before, we determine the most stable polaron for given values {tx, ty, E0}, by minimizing the energy with respect to the carrier wavefunction. We use a trial 2d Gaussian with variable widths σx and σy, of the form
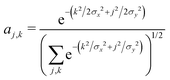 | (16) |
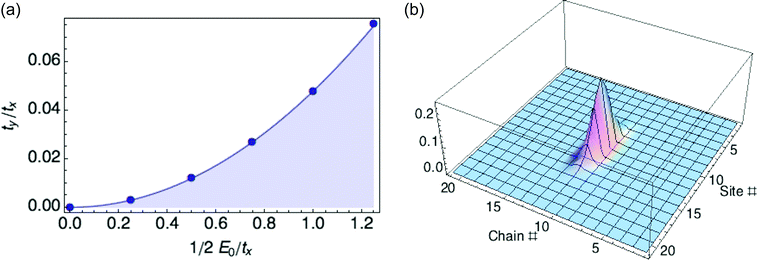
We organize our exploration of the three energy parameters as follows. The hopping parameter tx along a given chain sets the overall energy scale, so we measure E0 and ty in units of tx. When ty equals zero, we recover the 1d case and obtain a ring polaron for any value of E0. So we focus on what happens to the polaron binding energy as ty increases from zero for fixed E0. It turns out there is a critical value ty* as a function of reorganization energy E0, at which the optimized polaron has zero binding energy with respect to a delocalized carrier. Below ty*, the binding energy is negative; above ty*, the binding energy is positive, and the polaron is unstable to the extended state. We find ty*/tx equals 0.048(E0/tx)2, as shown in Fig. 4.
The 1d polaron becomes unstable to a delocalized carrier when the previously neglected transverse kinetic energy ty is large enough to cancel the polaron binding energy. The 1d polaron binding energy scales as E02/tx, so the transverse kinetic energy cost cancels the binding energy when ty/tx is of order (E0/tx)2, consistent with our numerical results.
Fig. 4b illustrates a 2D ring polaron for a hypothetical material with values of tx, ty, and E0 that correspond to the stable regime (see Fig. 4a). However, with values of tx, ty, and E0 for P3HT crystals (0.98 eV, 0.02 eV and 0.66 eV, respectively), we are in the unstable regime. Hence the transverse hopping, small as it is, is still enough to destabilize the 1d ring polaron. (ty was obtained from DFT calculations following the procedure described in our previous paper.6)
5 Dielectric polaron
A dielectric polaron forms as the dielectric medium around a chain with a hole or an excess electron is locally polarized by the extra charge. The induced local polarization interacts attractively with the carrier, which tends to localize it. This mechanism can occur both in crystalline and amorphous phases, whenever a chain with a carrier is surrounded by other polarizable material. For simplicity, we will study this mechanism in the absence of disorder, both along the chain with the carrier and in the surrounding medium, as would be the case in a perfect crystal.For both dielectric and ring polarons, the charge carrier is stabilized by attractive interactions with the change it induces in its surroundings. For the ring polaron, the change is the distortion of rings; for the dielectric polaron, the change is polarization of the medium. In both cases, the attractive interactions lower the onsite energy within the tight binding approximation.
Polarization can arise from two physically distinct mechanisms: displacement of atoms bearing partial charges, or electronic polarization. The former was emphasized in the original studies of polarons in ionic crystals. In ionic crystals, the dominant atomic displacements giving rise to polarization are optical phonons, in which the positively charged atoms in the lattice are displaced towards the added electron, and the negatively charged atoms move away. It would be helpful to know the relative importance of these two mechanisms to the polarizability of a P3HT crystalline lamella, before building a detailed model for dielectric polarons.
Dominant polarization mechanism
We want to know the dominant polarization mechanism in P3HT crystals. We can use classical MD simulations to determine the contributions from displacement of partial charges. Classical MD simulations do not include electronic polarization, and so will not capture electronic contributions to polarizability.If we had the experimental dielectric constant for crystalline P3HT, which reflects contributions from both electronic polarization and displacement of partial charges, we could subtract the partial charge displacement contributions from the total polarizability, to obtain the electronic contribution. However, we only have experimental dielectric constant values for the amorphous phase of P3HT, which is reported as εr ≈ 3 in P3HT melts at temperatures ranging from −50 °C to 50 °C.30
We can still get the values we need if we make the physically reasonable assumption that the electronic contribution to the polarizability is the same for amorphous and crystalline P3HT. Knowing the dielectric constant of the amorphous phase, we can determine the electronic contribution to P3HT polarizability by subtracting the contributions arising from the displacement of partial charges, again obtained from MD simulations of P3HT melt.
Separate molecular contributions to the dielectric constant of a material are not straightforwardly additive; rather, molecular contributions to the polarizability are additive, for intimately mixed gases and liquids. The Clausius–Mossotti relation connects the polarizability and the dielectric constant:
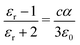 | (17) |
Note that cα/ε0 is dimensionless. The “polarizability volume” α′ conventionally defined as α′ ≡ α/(4πε0) is thus a molecular volume, which expresses the strength of molecular polarizability. For P3HT, we take the molecular unit to be a monomer (thiophene ring plus hexyl side chain). The monomer concentration is given by c = ρ/Mw, where Mw is the monomer molecular weight and ρ is the density.
We turn now to briefly describe simulation results for polarizability of crystalline and amorphous P3HT. There are two approaches to simulating polarizability: (1) apply an electric field and measure the induced system dipole; or (2) observe thermal fluctuations of the system dipole, and apply the fluctuation–dissipation theorem. For crystalline P3HT, we have applied the first approach; for amorphous P3HT, the second.
Crystalline P3HT is anisotropic, so the polarizability may depend on the direction of the applied field. Because of the lone pair on the sulfur atom, thiophene rings along the P3HT chain have sizable dipoles (about 1 Debye). In a crystalline lamella, the dipoles are oriented alternately up and down along the lamellar normal. In response to an electric field applied in the lamellar plane transverse to the chains, the rings rotate around the inter-ring bonds, slightly tipping the dipoles in the direction opposite the field. The polarizability is the proportionality constant χ of the polarization density P = χE in response to the field E. To observe it, we performed classical MD simulations of a P3HT lamella sheet at 300 K, 1 bar with electric fields ranging from 0.01 to 1 V nm−1 imposed in the π-stacking direction. Except for the dihedral potential for which we used parameters developed by Huang and co-workers,31,32 the forcefield parameters were directly obtained from the Optimized Potential for Liquid Simulations (OPLS)33 set, as implemented within the GROMACS34 MD package.
We found a polarization per ring of 0.0065 Debye V−1 nm−1, from the monomer molecular weight of 132 g mol−1 and a crystalline density of about 1.25 g cm−3, we find a volume per monomer V0 = 172 Å3, and a very small polarizability χ = P/(ε0E) of 0.014. Thus for the crystal, the dielectric constant ε = 1 + χ from deflecting the thiophene dipoles is scarcely different from unity; the crystal is so rigid that it prevents the dipoles from responding to the field.
We also use MD simulations to determine the polarizability from mobile partial charges, but this time by observing polarization fluctuations with no applied field. We perform NPT classical MD simulations of a P3HT amorphous melt at 700 K, and observe a system dipole variance 〈ΔM2〉 of 2716.9 Debye2 for a system of 1280 monomers. The dielectric constant is given by
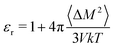 | (18) |
From these data, we determine a dielectric constant of 1.6, originating only from displacements in partial charges. Evidently thiophene dipoles are much more easily deflected by an applied field in a melt than in a crystal. We convert this dielectric constant to a polarizability volume using the Clausius–Mossotti relation and the monomer volume V0, to obtain αd′ = 6.85 Å3 (d for dipolar).
We can now estimate the electronic polarizability of the amorphous phase, by using the Clausius–Mossotti relation to “subtract” the contribution from thiophene dipoles from the experimental dielectric constant of about 3. Each monomer has two contributions to its molecular polarizability, which are additive. The total dielectric constant of ε = 3 corresponds to a total polarizability volume αt′ = 16.4 Å3. The electronic polarizability volume αe′ is then αt′ − αd′ = 9.59 Å3. Using Clausius–Mossotti to convert back again, the electronic-only dielectric constant is 1.9.
This is a reassuring result, in that the dielectric constant of many nonpolar liquids (including normal alkanes) are quite close to εr = 2. Although this value was inferred for the electronic polarizability of P3HT melts, it should apply to P3HT crystals as well, since electronic polarizability should be largely temperature-independent. Since the contribution from thiophene dipoles was negligible for crystals, we assume that for P3HT crystals εr = 2.0.
Dielectric polaron energy
To compute a dielectric polaron in a P3HT crystal, the kinetic energy is represented as before with a tight-binding model. The new feature is the interaction of the carrier wavefunction with the induced polarization in the surrounding medium. Our main assumption is to treat the polarizable medium as a classical continuum, interacting electrostatically with the localized carrier wavefunction.The carrier wavefunction is described by the tight binding model as a superposition of local HOMO or LUMO orbitals on each ring (for holes and electrons respectively). The probability distribution of the carrier presents a charge distribution to the dielectric. Because the carrier wavefunction describes the quantum mechanics of a single electron (or hole), its charge distribution does not interact with itself. Otherwise, since we assume the dielectric can be treated as a classical continuum, the electrostatic energetics are the same as for an equivalent classical charge distribution. We can therefore compute the energy as a sum of terms using methods of classical electrostatics, taking care to omit the self-energy of the charge distribution.
To proceed in more detail, we model the molecular orbitals crudely and conveniently as Gaussians, with a radius comparable to the size of a single ring. The charge qi = |ai|2 on the ith ring induces a polarization distribution Pi(r) in the surrounding material. By superposition, the total polarization distribution is the sum of the individual Pi(r) terms.
The classical electrostatic energy can be written as the sum over sites i and j of interactions between charges qi and qj, between qi and polarization Pj, and between Pi and Pj. (For the polaron, we omit the direct interaction between qi and qj as discussed above.) The building blocks for this sum are thus the electrostatic interactions between two Gaussian charge distributions, and the two polarizations distributions they induce. We use superposition arguments below to obtain the individual terms we require.
For any system of charges in a dielectric, the total electrostatic energy ET is the sum of charge–charge interactions EC, polarization–polarization interactions EP, and charge–polarization interactions ECP:
| ET = EC + EP + ECP | (19) |
Furthermore, we note that ET = EC/εr, since ET is the total electrostatic energy of the system with a given explicit charge distribution, and EC the electrostatic energy of the same distribution with no dielectric present. So ET − EC = EP + ECP implies
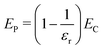 | (20) |
In particular, the total electrostatic energy of the polaron is:
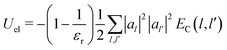 | (21) |
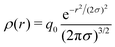 | (22) |
Then EC(l,l′) is given by
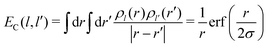 | (23) |
The interaction EC(l,l′) approaches 1/r for r large compared to σ, at which distance the two charge distributions appear pointlike. For r small compared to σ, the Coulomb singularity is cut off by the finite extent of the two charge distributions. Fig. 5 displays this result as a dimensionless function of r/σ, in units of the energy scale U0 = q02/(4πε0σ). The total polaron energy is the sum of the carrier kinetic energy and the electrostatic energy Uel:
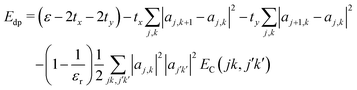 | (24) |
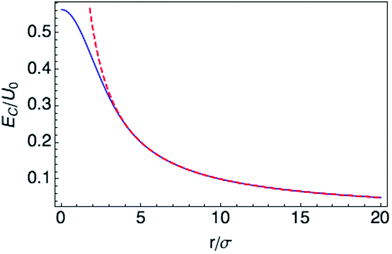 | ||
| Fig. 5 Interaction energy between two Gaussian charge distributions separated by r. Solid curve is eqn (23); dashed curve is 1/r, valid at large separations. | ||
Dielectric polaron ground state
To compute the polaron ground state, we minimize the energy eqn (24) over the shape of the carrier wavefunction, specified by the set of coefficients {aj,k}. Again we perform a variational calculation, in which we assume a 2d anisotropic Gaussian wavefunction and minimize Edp over its two characteristic widths.For parameter values relevant to P3HT (tx = 0.98, ty = 0.02 eV, εr = 2.0, and σ = 2 Å), we find a ground state with σx = 1.78 and σy = 0.11 monomers. The polaron mostly resides on a single chain. The carrier is localized over about 2.5 monomers (defined as before by twice the standard deviation for the probability distribution). Fig. 6a displays the carrier probability distribution. This narrow dielectric polaron has a correspondingly large binding energy (0.46 eV for σ = 2 Å), well in excess of kT. Such a large binding energy indicates that the dielectric polaron in a P3HT lamella is very stable at ambient temperature. This is in direct contrast to the ring polaron, which was shown to not form at all.
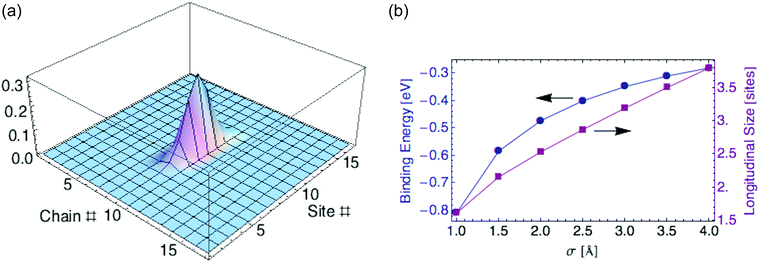 | ||
| Fig. 6 (a) Carrier density for dielectric polaron in P3HT crystalline lamella. (b) Binding energy and polaron size versus charge distribution width σ. | ||
Recall we have represented the localized carrier orbitals (HOMO or LUMO on each ring, for hole or electron carriers respectively) as Gaussian charge distributions of characteristic width σ. The dielectric polaron size and binding energy are sensitive to the value of σ, as Fig. 6b shows.
Our estimate of σ = 2 Å is based on the observation that the HOMO and LUMO molecular orbitals are localized to one ring, and the spacing between adjacent rings along the P3HT backbone is about 4 Å. Since the precise shape of the molecular orbitals is not Gaussian, and the best value of σ is uncertain, the predicted dielectric polaron size and binding energy should be regarded as a range of values.
The above analysis is also relevant to dielectric polarons on a straight section of chain in an amorphous phase. For a chain in an amorphous phase, there are typically no aligned adjacent chains for a carrier to hop to, so the transverse hopping terms in the Hamiltonian would be absent. But since the dielectric polaron in a crystalline lamella is largely confined to a single chain, the effect of this change should be small. More significantly, the amorphous phase has a larger dielectric constant (εr = 3) than the crystal (εr = 2), because of the contribution to the polarizability from alignment of thiophene dipoles. However, this contribution responds very slowly, on the timescale for dipoles to reorient by diffusion; it may be more physical to regard the field from thiophene dipoles on other chains as a quenched random field.
In our analysis of the dielectric polaron, for simplicity we neglected any coupling to ring modes. Actually, charge carriers interact with the dielectric medium and ring modes simultaneously. When we combine both effects in a single calculation, a polaron in a crystalline lamella has a binding energy of 0.55 eV (for σ = 2 Å), which is 90 meV more strongly bound as a result of coupling to the ring modes. This contribution is nine times larger than the binding energy of the ring polaron alone; ring modes contribute more strongly when combined with the dielectric mechanism, because the carrier is already localized by the polarization.
Charge modulation spectroscopy (CMS) can probe the electronic state of charge carriers present in the active layer of field effect transistors (FETs). Charges are injected into the semiconducting film by applying a gate voltage. The injected charges form polarons, upon rearrangement of the local environment. The electronic energy levels of the polarons are shifted by the polaron stabilization energy with respect to extended states. Electrons from the valence band can be excited by light absorption to fill hole polarons within the band gap. The corresponding optical transitions can be observed by UV-vis spectroscopy. CMS thus allows for the spectroscopic signature of polarons to be detected.35,36
CMS experiments on highly ordered P3HT films find a hole-polaron stabilization energy of around 0.35 eV,35–37 with values as high as 0.4 and 0.5 eV reported for isolated chains imbedded in a matrix and for amorphous films, respectively.38 These stabilization energies are much larger than the reorganization energy resulting from nuclear displacements alone, and so cannot be explained by a polaron stabilized by this mechanism alone. Indeed, in Section 4 we showed that ring relaxation alone is too weak to localize charge carriers and form polarons in ordered P3HT lamellae. In the absence of disorder in the crystal, by which the carriers would be already localized, polarons will not form if ring relaxation were the only stabilizing mechanism. Pochas and Spano39 and Ghosh et al.40 simulated the CMS spectra of P3HT films, taking into account only nuclei relaxation as stabilizing effect. They were able to reproduce experimental spectra only by assuming (1) substantial static disorder and (2) unrealistically large interchain hopping parameters.
Polaron stabilization energies obtained from CMS are consistent with dielectric effects being the main mechanism for polaronic stabilization of charge carriers, supplemented by nuclear relaxation. The reported values fall well within the range of binding energies computed in this work, given the uncertainty in the width of the local charge densities σ (see Fig. 6b).
CMS spectroscopic data have previously been interpreted as evidence that charge carriers (polarons) in P3HT are delocalized over several chains.35,36,38,41 This contrasts with our finding that the polaron largely resides on a single chain, with only a small leakage of its amplitude to adjacent chains. The previous interpretation of CMS data rests on the observation that the polaron binding energy decreases slightly (the lowest polaronic level is red-shifted) when going from a single chain to highly ordered P3HT films (<0.1 eV38), or when increasing the regio-regularity of the P3HT film (0.05 eV between 81% and 96%36). This reduction in binding energy can be explained by the additional interchain hopping, which competes with the stabilizing reorganization of the medium (dielectric and nuclear). However, this qualitative argument does not predict the extent of delocalization across chains quantitatively. Note that the degree of stabilization will also change as the dielectric constant changes, from a chain in an inert matrix or solution to a chain in the ordered film. The modest reported changes in polaron binding energy are in a range that we can account for by small changes in the strength of interchain hopping ty and/or the dielectric constant εr. The decrease in binding energy is accompanied by an increase in the polaron width in the interchain direction, but even with ty as high as 0.1 eV, the polaron still largely resides on a single chain in the lamella.
Other proposed arguments suggestive of delocalization across chains include the emergence and increase in intensity of (1) excitations between the valence top and the highest polaronic level (which is forbidden by symmetry for isolated chains), and (2) low energy charge-transfer (CT) excitations (excitations between occupied polaronic levels, and polarized in the interchain direction41), when going from isolated chains to films of increasing order. These two arguments point towards an increased interchain coupling, but like the reduced binding energy above, they do not provide a quantitative estimate of the extent of delocalization of the carriers across chains.
Scaling argument for dielectric polaron
In retrospect, we can give a scaling argument to show why a dielectric polaron forms robustly, even in multiple dimensions. The stabilization energy from polarization scales differently with polaron size than stabilization from coupling to ring modes.For simplicity, consider a spherically symmetric charge distribution of spatial extent R, beyond which the medium is polarized. The induced polarization a distance r from the center of the charge distribution is proportional to the local field, which falls off with distance as 1/r2. This polarization in turn produces a dipole potential, which likewise varies as 1/r2. The induced dipoles are oriented radially, such that the dipole interacts attractively with the charge. The attractive interaction of the charge with a volume element a distance r away scales as 1/r4.
The total attraction is the integral over all space outside the charge distribution, which scales as −1/R in three dimensions. The kinetic energy of the carrier wavefunction as usual scales as 1/R2; hence the sum of the two terms generically has a minimum in R, whatever may be the coefficients of the kinetic and attractive energies.
6 Polaronic effects on carrier motion
Polarons can have important effects on the motion of charge carriers. As a polaron moves through, rings along the chain distort then recover their neutral shape. The associated kinetic energy of the moving atoms adds to the carrier effective mass. If the polaron moves by quickly enough, the rapid perturbation of the rings can excite oscillations in the ring modes. These oscillations remove energy from the moving polaron, damping its velocity. Below, we estimate the importance of these mechanisms for polarons in crystalline P3HT lamellae.Effective mass
We want to estimate the contribution to the effective mass of a polaronic charge carrier from the motion of atoms on rings, which distort and recover as the polaron moves past. Consider a polaron moving at velocity v along a chain. The carrier probability |ak|2 is given by a moving Gaussian envelope function| |ak|2 = f(kΔ − vt) | (25) |
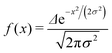 | (26) |
As the polaron moves past, the distortion on a given ring grows from zero to its maximum in the middle of the polaron and then decreases again to zero. If we sum this kinetic energy over all the rings along the chain, by translational invariance we obtain a time-independent result. This ring kinetic energy will scale as v2, with a coefficient δm that is the contribution of the ring motion to the carrier effective mass.
To compute δm, we write the energy of the ring normal modes as:
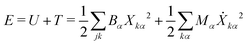 | (27) |
Next we specialize to the single deformation mode, under which the normal modes amplitudes on each site are given by Xkα = (Cα/Bα)Xk. The kinetic energy of the single deformation mode becomes, after a bit of algebra
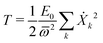 | (28) |
![[small omega, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0da.gif) of the single mode by
of the single mode by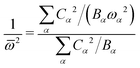 | (29) |
From our earlier discussion, the distortion on the kth ring Xk = −|ak|2, with time derivative given by
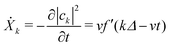 | (30) |
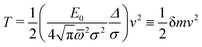 | (31) |
For P3HT, the characteristic energy for the reorganization of rings is E0 = 0.66 eV, the average frequency of the modes involved (see Appendix) computed from (29) is ![[small omega, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0da.gif) = 770 cm−1, and Δ = 3.9 Å. The polaron stabilized by ring and dielectric effects combined has a probability distribution of width 2σ = 2.26Δ, resulting in δm of 0.06 electron masses. For comparison to the bare hole, recall that the tight-binding model for a periodic chain has a cosine band, of the form ε(k) = ε0 − 2t
= 770 cm−1, and Δ = 3.9 Å. The polaron stabilized by ring and dielectric effects combined has a probability distribution of width 2σ = 2.26Δ, resulting in δm of 0.06 electron masses. For comparison to the bare hole, recall that the tight-binding model for a periodic chain has a cosine band, of the form ε(k) = ε0 − 2t![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos(k), which for small k can be expanded as ε(k) = ε0 − 2t + tΔ2k2. Equating the quadratic term to the carrier kinetic energy ħ2k2/(2meff), we have meff = ħ2/(2tΔ2). For Δ ≈ 4 Å and t ≈ 1 eV, this gives meff ≈ 0.25 electron masses. Polaronic effects add about 25 percent to the hole effective mass.
cos(k), which for small k can be expanded as ε(k) = ε0 − 2t + tΔ2k2. Equating the quadratic term to the carrier kinetic energy ħ2k2/(2meff), we have meff = ħ2/(2tΔ2). For Δ ≈ 4 Å and t ≈ 1 eV, this gives meff ≈ 0.25 electron masses. Polaronic effects add about 25 percent to the hole effective mass.
Excitation of ring modes
Now we assess whether ring normal modes are excited by a passing polaron. If a polaron passes by a given ring rapidly compared to the periods of the normal modes, the transit of the polaron past the ring can excite these modes to oscillate. These oscillations will remove energy from the moving polaron and thus damp its velocity, acting as a drag on the polaron.To see how important this effect is, we need to know the typical velocities with which polarons move. Polarons are constructed from quasiparticles, either holes added to the full valence band or electrons added to the empty conduction band, whether by chemical or electrostatic doping. A typical charge carrier fraction for thin-film electronic devices is about one per 100 rings,42,43 which ultimately establishes the maximum Fermi level for the quasiparticles. In the semiclassical approximation, quasiparticles of wavenumber k move as wavepackets with velocity kħ/meff, where meff is the effective carrier mass obtained from the band curvature at k = 0. To determine the quasiparticle Fermi velocity, we need the quasiparticle Fermi momentum kF and the carrier effective mass.
The conduction and valence band of P3HT chains contain a maximum of one charge carrier per ring; since there are one pair of states per wavenumber, the maximum wavenumber (at the band edge) is k = π/Δ. If one percent of the states are occupied, the quasiparticle Fermi momentum is kF = π/(100Δ), with a corresponding quasiparticle Fermi velocity of ħπ/(100Δmeff).
Then the quasiparticle Fermi velocity vF = ħπ/(100Δmeff) is approximately 35 km s−1. At this velocity, the time for the polaron to move by one ring is about 10 fs. So for the combined ring and dielectric polaron of width 2σ = 2.3 rings, the transit time is about 23 fs. For comparison, the period corresponding to the effective frequency of 770 cm−1, as computed from (29), is about 50 fs. From these values, the polaron transit time is somewhat smaller than the average oscillation period of the normal modes contributing to ring reorganization. This means that at the highest carrier densities, moving polarons may tend to excite ring oscillations. A more detailed estimate of the damping from this effect is beyond the scope of this paper.
7 Carrier localization by dihedral disorder
Another way to assess the strength of polaronic effects is to compare the size and binding energy of polarons to the localizing effects of dihedral disorder. This comparison is relevant to amorphous melts, in which chains will have relatively straight sections as well as “kinks” resulting from dihedral rotations that tend to break conjugation and localize carriers. In a quenched random configuration of dihedral angles, states localized to relatively straight chain segments with higher hopping matrix elements will have lower energy than delocalized states. This gives rise to an effective binding energy for disorder-localized states relative to delocalized states.In previous work, we presented a tight-binding model that captures the effects of dihedral disorder on the valence and conduction states of P3HT chains.6 Each random chain configuration has its own set of eigenstates. To compare disorder-induced localization with polaronic effects, we focus on the properties of the lowest-lying hole state, which we sample over 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 conformations of disordered 100mer P3HT chains. Fig. 7a shows the lowest-lying states for six such chains. For each such state, we measure the carrier density localization length given by
000 conformations of disordered 100mer P3HT chains. Fig. 7a shows the lowest-lying states for six such chains. For each such state, we measure the carrier density localization length given by
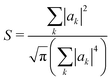 | (32) |
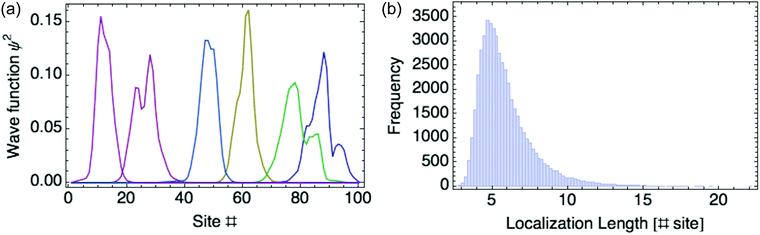 | ||
| Fig. 7 (a) Six typical lowest-lying states for disordered P3HT 100-mer chains. (b) Histogram of localization lengths. | ||
Fig. 7b gives a histogram of localization lengths, with an average length of 6 rings.
The average size of the most localized states is about six rings; the average binding energy is 97 meV, about 4kT at room temperature; dielectric polarons on P3HT chains in melts are even narrower and more tightly bound than this, indicating that polaronic effects are significant even on disordered chains.
Our polaron calculations were made in the absence of disorder. But our predictions would still hold even with the inclusion of realistic structural disorder of chains in the melt or in the crystal, since in both phases the states localized by disorder alone are wider than dielectric polarons or polarons stabilized by the combined effect of dielectric and ring reorganization.
8 Conclusions
We have developed a tight-binding model of electrons and holes on P3HT chains to study mechanisms for polaron formation in P3HT crystals and melts. This work builds on our previous model for the effects of dihedral disorder on electronic states of single P3HT chains in solution.6 Here, we add (1) local vibrational modes of monomers that deform in response to onsite charges, (2) coupling of charges along a chain to the surrounding dielectric medium, and (3) hopping matrix elements between pi-stacked rings on adjacent chains in a P3HT crystal.Polarons generally can be thought of as an attractive interaction between an excess charge in a semiconductor or insulator, and the distortions it induces in the surrounding medium. Coupling to monomer vibrational modes and dielectric polarization are two possible mechanisms for polaron formation. We assessed the relative importance of these two mechanisms, using realistic parameters derived from DFT calculations, monomer architecture, and experimental and simulation results for dielectric response.
For monomer vibrational modes, we used DFT to compute the eigenvector of the response to a localized hole, the spring constant for this mode, and the coupling constant to the onsite charge carrier. We showed that a simplified Holstein model in which charge carriers on a monomer couple to a single mode of distortion is equivalent to previous approaches in which carriers couple to multiple normal modes of the monomers.
We used this simplified model to compute the width and binding energy of a polaron stabilized by distortions of the P3HT backbone rings (monomers). On a single straight chain, this mechanism for polaron formation is quite weak, resulting in broad polarons (10 rings wide) with very small binding energies (only 10 meV). We extended these calculations to ring polaron formation in a P3HT crystalline lamella, and find that the small transverse hopping matrix element is enough to destabilize the polaron with respect to the fully delocalized state.
We have also investigated dielectric polarons in P3HT crystalline lamella. Here the stabilization mechanism is similar to polarons originally considered in ionic crystals; the charge carrier induces polarization in surrounding material, which in turn attracts the carrier to remain in a given locale. Polarization in P3HT can arise either from displacement of nearby atoms bearing partial charges, or by electronic polarization of valence electrons on nearby moieties. We assessed the relative contributions of these two polarization mechanisms, and concluded that electronic polarization is dominant for crystalline P3HT.
We constructed a model for dielectric polaron formation in which the polarization of the surrounding medium is treated classically, while the excess hole or electron is described with a tight-binding model. Wavefunction amplitudes of the single excess carrier on different monomers do not have a direct Coulomb interaction (a single electron or hole does not repel itself). However, amplitudes on different monomers do interact attractively through their attraction to the induced polarization. This attraction, balanced against the kinetic energy of the carrier, determines the polaron size and binding energy.
The resulting polaron is about 2.5 rings wide with a binding energy of 460 meV. Similar values should apply as well for polarons stabilized by electronic polarization on straight sections of chains in P3HT melts. For comparison, we computed as well the typical size of localized states on single chains with dihedral disorder in P3HT melts. We found dihedral disorder leads to localized states about 6 rings wide on average, with a binding energy of around 100 meV relative to delocalized carriers. Thus dielectric polaron formation may be relevant even to charge carriers in P3HT melts.
Conflicts of interest
There are no conflicts of interest to declare.Appendix
A conventional treatment of monomer vibrational modes coupled to charge carriers on P3HT begins with the full set of 21 normal modes for each thiophene ring monomer. The Hamiltonian eqn (2) used in the literature includes multiple normal modes, a spring constant Bα and a coupling constant Cα for the αth mode. Each of these can be computed using DFT, by imposing the corresponding normal mode distortion and computing the energy with and without an excess charge present.Relatively few normal modes respond significantly to stabilize a charge on a ring. The combination of coefficients Cα2/Bα for mode α determines its contribution to stabilizing a localized charge on the monomer. We can use DFT to compute the coupling constants for the normal modes, in much the same way as for the composite single mode. However, this would be tedious to do for all the normal modes, as was done in previous work.17
We can determine which normal modes are most important in stabilizing a charge by expanding the “composite mode”—the eigenvector of displacements in response to a localized charge—in normal modes. We then compute the coupling constants only for the modes that contribute most to the composite mode. As for the composite mode, we perform DFT calculations on a unit cell with two rings (see Fig. 1). The eigenvectors of the Hessian for this unit cell are the 42 normal modes, with their associated frequencies.
To carry out this expansion of the composite mode, we must choose a normalization of the normal modes. Conventionally, we define the normal mode eigenvectors {eα} to have some fixed norm. For convenience, we choose their norm to be the same as that of the collective mode eigenvector e. Then we can compute the normal mode amplitudes in the presence of a charge in two ways. First, we can expand e in the set of {eα} as 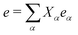 , so that Xα = e·eα/(e·e) (where we used e2 = eα2). Second, we can compute Xα by minimizing the Hamiltonian, as Xα = −Cα/Bα. These two expressions for Xα should be equal.
, so that Xα = e·eα/(e·e) (where we used e2 = eα2). Second, we can compute Xα by minimizing the Hamiltonian, as Xα = −Cα/Bα. These two expressions for Xα should be equal.
Fig. 8a displays the frequencies of these 42 modes in rank order, and 8b their inner products with the composite mode (response to a hole), scaled so that the sum of squares of the normal mode amplitudes is unity.
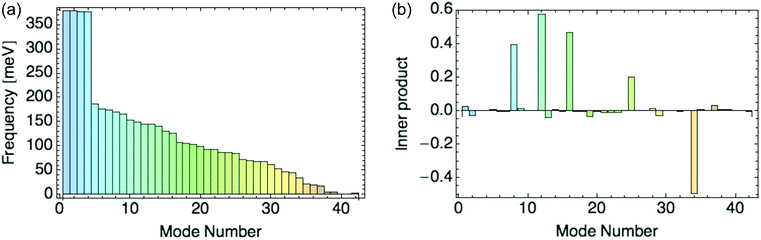 | ||
| Fig. 8 (a) Normal mode frequencies. (b) Inner product of normal modes with the composite mode induced by a hole. | ||
We focus on the six dominant normal modes {8, 9, 12, 16, 25, 34} out of 42 with the largest projections on the composite mode, and add modes 1 and 2 as small-amplitude “controls” to test our selection criterion. We include mode 9, as its projection increases for a composite mode obtained from a response to higher hole densities per ring. The six dominant modes are all symmetric across the unit cell, i.e. they distort the two rings identically.
Fig. 9 presents example results for mode 12, for the spring constant Bα (a) and coupling constant Cα (b). Fig. 9b illustrates the effects of a large carrier density on the effective coupling constant. (Evidently for charge per ring |ψ|2 above 0.5, the simple form of the electron–phonon coupling must be modified for quantitative agreement with DFT results, but even then the quantitative effects are small.)
Table 1 presents the spring and coupling constants for the eight selected modes. Evidently, the dominant modes all have large values of the coupling parameter Cα2/Bα, relative to the “control” modes 1 and 2 that did not project much onto the composite mode. Also, the two ways of computing the normal mode amplitudes Xα match well (last two columns), except for mode 9, whose projection becomes significant at higher hole densities per ring. Finally, the sum of the reorganization energies per site 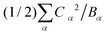 equals 0.33 eV, consistent with the composite mode value (0.33 eV).
equals 0.33 eV, consistent with the composite mode value (0.33 eV).
| Mode # | B α (eV) | C α (eV) | C α 2/Bα (eV) | C α /Bα | e·eα/(e·e) |
|---|---|---|---|---|---|
| 1 | 0.96 | −0.020 | 0.0004 | 0.02 | 0.03 |
| 2 | 0.96 | 0.019 | 0.0004 | −0.02 | −0.03 |
| 8 | 1.49 | −0.628 | 0.264 | 0.42 | 0.39 |
| 9 | 1.18 | 0.238 | 0.048 | −0.20 | 0.01 |
| 12 | 1.03 | −0.486 | 0.230 | 0.47 | 0.58 |
| 16 | 0.36 | −0.108 | 0.033 | 0.30 | 0.47 |
| 25 | 0.64 | −0.138 | 0.030 | 0.22 | 0.20 |
| 34 | 0.20 | 0.107 | 0.057 | −0.53 | −0.50 |
References
- F. Garnier, R. Hajlaoui, A. Yassar and P. Srivastava, Science, 1994, 265, 1684–1686 CAS.
- J. H. Burroughes, D. D. C. Bradley, A. R. Brown, R. N. Marks, K. Mackay, R. H. Friend, P. L. Burns and A. B. Holmes, Nature, 1990, 347, 539–541 CrossRef CAS.
- N. S. Sariciftci, L. Smilowitz, A. J. Heeger and F. Wudl, Synth. Met., 1993, 59, 333–352 CrossRef CAS.
- L. D. Landau, Phys. Z. Sowjetunion, 1933, 3, 664 CAS.
- P. W. Anderson, Phys. Rev., 1958, 109, 1492–1505 CrossRef CAS.
- J. H. Bombile, M. J. Janik and S. T. Milner, Phys. Chem. Chem. Phys., 2016, 18, 12521–12533 RSC.
- R. A. Street, Science, 2013, 341, 1072–1073 CrossRef CAS PubMed.
- M. Mladenović and N. Vukmirović, Adv. Funct. Mater., 2015, 25, 1915–1932 CrossRef.
- W. Barford, J. Phys. Chem. A, 2013, 117, 2665–2671 CrossRef CAS PubMed.
- M. D. Newton, Chem. Rev., 1991, 91, 767–792 CrossRef CAS.
- Z. G. Yu, D. L. Smith, A. Saxena, R. L. Martin and A. R. Bishop, Phys. Rev. Lett., 2000, 84, 721–724 CrossRef CAS PubMed.
- F. C. Grozema, P. T. van Duijnen, Y. A. Berlin, M. A. Ratner and L. D. A. Siebbeles, J. Phys. Chem. B, 2002, 106, 7791–7795 CrossRef CAS.
- L. D. A. Siebbeles, F. C. Grozema, M. P. De Haas and J. M. Warman, Radiat. Phys. Chem., 2005, 72, 85–91 CrossRef CAS.
- D. Alberga, A. Perrier, I. Ciofini, G. F. Mangiatordi, G. Lattanzi and C. Adamo, Phys. Chem. Chem. Phys., 2015, 17, 18742–18750 RSC.
- T. Holstein, Ann. Phys., 1959, 8, 325–342 CAS.
- T. Holstein, Ann. Phys., 1959, 8, 343–389 CAS.
- K. D. Meisel, H. Vocks and P. A. Bobbert, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 71, 1–6 CrossRef.
- O. R. Tozer and W. Barford, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 89, 1–7 CrossRef.
- R. P. Fornari and A. Troisi, Phys. Chem. Chem. Phys., 2014, 16, 9997–10007 RSC.
- W. Barford, M. Marcus and O. R. Tozer, J. Phys. Chem. A, 2016, 120, 615–620 CrossRef CAS PubMed.
- E. Mozafari and S. Stafström, J. Chem. Phys., 2013, 138, 184104 CrossRef CAS PubMed.
- L. A. Ribeiro Junior and S. Stafström, Phys. Chem. Chem. Phys., 2015, 17, 8973–8982 RSC.
- J. M. Frost, J. Kirkpatrick, T. Kirchartz and J. Nelson, Faraday Discuss., 2014, 174, 1–12 RSC.
- P. F. Barbara, T. J. Meyer and M. A. Ratner, J. Chem. Phys., 1996, 100, 13148–13168 CrossRef CAS.
- J.-L. Brédas, D. Beljonne, V. Coropceanu and J. Cornil, Chem. Rev., 2004, 104, 4971–5004 CrossRef PubMed.
- R. P. Fornari, J. Aragó and A. Troisi, J. Chem. Phys., 2015, 142, 184105 CrossRef PubMed.
- V. M. Geskin, A. Dkhissi and J. L. Brédas, Int. J. Quantum Chem., 2003, 91, 350–354 CrossRef CAS.
- V. M. Geskin and J. L. Brédas, ChemPhysChem, 2003, 4, 498–505 CrossRef CAS PubMed.
- A. Chaalane, D. Mahi and A. Dkhissi, Theor. Chem. Acc., 2015, 134, 66 CrossRef.
- R. Xie, Y. Lee, M. P. Aplan, N. J. Caggiano, C. Müller, R. H. Colby and E. D. Gomez, Macromolecules, 2017, 50, 5146–5154 CrossRef CAS.
- D. M. Huang, R. Faller, K. Do and A. J. Moule, J. Chem. Theory Comput., 2010, 6, 526–537 CrossRef CAS PubMed.
- K. N. Schwarz, T. W. Kee and D. M. Huang, Nanoscale, 2013, 5, 2017 RSC.
- W. L. Jorgensen, J. D. Madura and C. J. Swenson, J. Am. Chem. Soc., 1984, 106, 6638–6646 CrossRef CAS.
- D. Van Der Spoel, E. Lindahl, B. Hess, G. Groenhof, A. E. Mark and H. J. C. Berendsen, J. Comput. Chem., 2005, 26, 1701–1718 CrossRef CAS PubMed.
- P. J. Brown, H. Sirringhaus, M. Harrison, M. Shkunov and R. H. Friend, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 63, 125204 CrossRef.
- H. Sirringhaus, P. J. Brown, R. H. Friend, M. M. Nielsen, K. Bechgaard, B. M. W. Langeveld-Voss, A. J. H. Spiering, R. A. J. Janssen, E. W. Meijer, P. Herwig and D. M. de Leeuw, Nature, 1999, 401, 685–688 CrossRef CAS.
- C. Cobet, J. Gasiorowski, R. Menon, K. Hingerl, S. Schlager, M. S. White, H. Neugebauer, N. S. Sariciftci and P. Stadler, Sci. Rep., 2016, 6, 35096 CrossRef PubMed.
- R. Osterbacka, C. P. An, X. M. Jiang and Z. V. Vardeny, Science, 2000, 287, 839–842 CrossRef CAS PubMed.
- C. M. Pochas and F. C. Spano, J. Chem. Phys., 2014, 140, 244902 CrossRef PubMed.
- R. Ghosh, C. M. Pochas and F. C. Spano, J. Phys. Chem. C, 2016, 120, 11394–11406 CAS.
- D. Beljonne, J. Cornil, H. Sirringhaus, P. J. Brown, M. Shkunov, R. H. Friend and J.-L. Brédas, Adv. Funct. Mater., 2001, 11, 229–234 CrossRef CAS.
- T. P. Le, Z. Shang, L. Wang, N. Li, S. Vajjala Kesava, J. W. O'Connor, Y. Chang, C. Bae, C. Zhu, A. Hexemer, E. W. Gomez, A. Salleo, M. A. Hickner and E. D. Gomez, Macromolecules, 2015, 48, 5162–5171 CrossRef CAS.
- M. Panzer and C. Frisbie, Adv. Funct. Mater., 2006, 16, 1051–1056 CrossRef CAS.
| This journal is © the Owner Societies 2018 |