A DFT study of H-dissolution into the bulk of a crystalline Ni(111) surface: a chemical identifier for the reaction kinetics

Abstract

In this study, we investigated the diffusion of H-atoms to the subsurface and their further diffusion into the bulk of a Ni(111) crystal by means of density functional theory calculations in the context of thermal and plasma-assisted catalysis. The H-atoms at the surface can originate from the dissociative adsorption of H₂ or CH₄ molecules, determining the surface H-coverage. When a threshold H-coverage is passed, corresponding to 1.00 ML for the crystalline Ni(111) surface, the surface-bound H-atoms start to diffuse to the subsurface. A similar threshold coverage is observed for the interstitial H-coverage. Once the interstitial sites are filled up with a coverage above 1.00 ML of H, dissolution of interstitial H-atoms to the layer below the interstitial sites will be initiated. Hence, by applying a high pressure or inducing a reactive plasma and high temperature, increasing the H-flux to the surface, a large amount of hydrogen can diffuse in a crystalline metal like Ni and can be absorbed. The formation of metal hydride may modify the entire reaction kinetics of the system. Equivalently, the H-atoms in the bulk can easily go back to the surface and release a large amount of heat. In a plasma process, H-atoms are formed in the plasma, and therefore the energy barrier for dissociative adsorption is dismissed, thus allowing achievement of the threshold coverage without applying a high pressure as in a thermal process. As a result, depending on the crystal plane and type of metal, a large number of H-atoms can be dissolved (absorbed) in the metal catalyst, explaining the high efficiency of plasma-assisted catalytic reactions. Here, the mechanism of H-dissolution is established as a chemical identifier for the investigation of the reaction kinetics of a chemical process.

---

Introduction

The interaction of hydrogen with transition metals has been extensively studied by both experimental and theoretical methods for several decades.¹ In heterogeneous catalysis, Ceyer and co-workers^2–4 studied the kinetics of subsurface hydrogen (bulk H-atoms) in the active Ni metal phase that has a crucial role in the hydrogenation of alkenes and alkynes. However, a microscopic understanding of the H-kinetics for different H-coverages is largely missing. Dissociative adsorption of H₂ on a Ni surface has been extensively studied before.^5–7 Here, the H-kinetics of dissociative adsorption of H₂ or, equivalently, the associative desorption of H₂, and the dissolution of surface-bound H-atoms are investigated for different H-coverages at the Ni(111) surface. Ultimately, we will show the formation of nickel hydride in a catalytic process by applying high pressure or reactive plasma.

In this study, the concept of H-diffusion to the subsurface of the metal catalyst, which is initiated by applying a high pressure or inducing a reactive plasma and high temperature, is applied to the above process. The higher rate of H-diffusion to the subsurface gives rise to a higher H-absorption on the specific crystalline surface of the metal. This results in the reduction of surface-bound H-atoms and consequently the increase the rate of products rather than reactants.

The amount of stored H varies from metal to metal. Here, we do not calculate the amount of stored H in a metal. In this study, we show how this energetic bulk hydrogen can be formed by either inducing the reactive plasma or applying high pressure and temperature, which make these routes amenable to the hydrogenation reaction in any catalytic process.

The adsorbate–surface interaction depends on the coverage of adsorbates, crystal planes, and reaction conditions.^8,9 The open surface structure is often more catalytically active than those with closely packed surface atoms. Depending on the reaction conditions, a different coverage of adsorbates may be formed. This may ultimately result in surface reconstruction, which modifies the entire reaction kinetics at the surface. Here, we study the H-diffusion to the subsurface of the Ni(111) facet, which is more closely packed than the Ni(110) and Ni(100) facets.

Traditionally, in a thermal catalytic process, the conversion of gas molecules into the targeted products occurs at high pressure and temperature. For instance, both for the steam reforming¹⁰ and dry reforming of methane,¹¹ high temperature (800–1000 °C) and high pressure (3–25 bar) are utilized to produce hydrogen from the methane gas. Non-thermal plasmas are highly reactive due to the presence of energetic electrons and reactive species (free radicals, excited molecules, and ions).^12,13 The energetic electrons, with a typical energy of 1–10 eV, create a distinct nonequilibrium plasma with an overall gas kinetic temperature as low as room temperature. As a result, molecular fragments can be formed at a low temperature and in a very wide pressure range. Hence, the reaction conditions of thermal catalysis, typically requiring high pressure and high temperature, can be replaced by a non-thermal plasma.

The interaction of electronically excited molecules with the surface cannot be studied using conventional ground-state DFT calculations. This type of interaction can be studied by time-dependent DFT (TDDFT). However, here we assumed that upon dissociation of a hydrogen source in the plasma phase, they are mostly formed in their electronic ground states, and upon interaction with the surface they also adsorb in their electronic ground states. This assumption indeed corresponds to both experimental and modeling results, indicating that the densities/fluxes of electronically excited species are typically many orders of magnitude lower than the densities of ground-state species.^14,15

In the above processes, the surface-bound or bulk H-atoms are created from the scission of a C–H bond in CH₄ and an O–H bond in H₂O, or the H–H bond in H₂. In the former case, since CH₄ and H₂O are chemically inert and thermodynamically stable, the pressure and temperature of the gas species are elevated to break the inert molecule at the surface of a typical catalyst like Ni. In the latter case, H₂ dissociates to form surface-bound H-atoms depending on the type of metals.^5,16 The relationship between the position of the band centre (C_d) and the activation energy for desorption (E_a) was studied before.^16,17 As the energy of C_d shifts downward away from the Fermi level, more antibonding states are occupied, which gives rise to weaker metal–hydrogen bonding, and hence a lower E_a.

The dissociative adsorption of H₂ or CH₄ molecules at the surface eventually stops, since previous dissociation reactions resulting in surface-bound H-atoms deactivate the surface sites to further dissociation. Hence, the H-atoms either should be consumed by other reactants to form the targeted products or should desorb as H₂. In both cases, the surface sites would be released to sustain the chemical reactivity of the surface.

However, another distinct possibility is diffusion of surface-bound H-atoms to the subsurface. When both the flux of incoming H-atoms and the H-coverage are large, the subsurface sites will be occupied to some extent. The formation rate of H-atoms largely depends on either the reactivity of the surface site to dissociation of H₂ in a thermal process or direct adsorption of H-atoms in a plasma process. Furthermore, the H-coverage depends on the stiffness of a crystal plane of a metal to preserve H-atoms at the surface. The occupation of subsurface sites largely depends on the temperature. A high temperature increases the mobility of bulk H-atoms between interstices and facilitates the internal equilibrium.¹⁸ Hence, depending on the rate of incoming H-atoms, temperatures and crystal planes, different metals exhibit very different levels of hydrogen content. In this paper, we provide a microscopic understanding of bulk H-atom formation at a crystalline Ni(111) surface by means of density functional theory (DFT) calculations.

Recently, we showed that most plasma-assisted catalytic hydrocarbon reactions proceed faster in the presence of a high H-coverage.¹⁹ In other words, the hydrogenation of an open shell molecule at the catalyst surface is facilitated due to the high coverage of surface-bound H-atoms. The presence of surface-bound H-atoms can essentially control the course of chemical reactions at the surface. Hence, it is of interest to find out to what extent H-diffusion to the subsurface could contribute to the rate of hydrogenation. The first aim of this research is to gather the detailed chemical kinetics of H-atoms at a crystalline Ni(111) surface at the micro-scale, to be implemented in kinetic Monte Carlo (KMC) calculations.²⁰ The accuracy of KMC calculations, as a coarse grained model, strongly depends on the identified chemical reactions.²¹ In the current study, we investigate H-absorption at the Ni(111) facet. The combination of DFT and KMC^22,23 including all identified chemical reactions, allows the identification of the role of H-absorption on the reaction kinetics at the Ni(111) facet.

The importance of H-dissolution in a metal is by no means limited to the reaction kinetics of catalysis or plasma catalysis. It is also applicable to hydrogen storage,²⁴ the purification of hydrogen, the development of fuel cells,^25,26 metal growth by atomic layer deposition,²⁷ and the growth of carbon nanotubes.²⁸ Hence, the second aim of this research is to establish the mechanism of H-dissolution in a transition metal as a chemical identifier to investigate the consequence of the formation of metal hydride on the reaction kinetics of a targeted process. For instance, this chemical identifier already showed that metallic Pd has the highest H-replenishment among the transition metals, which is in excellent correspondence with the experiment.²⁹

Computational details

To study the interaction of H-atoms with a Ni catalyst, self-consistent DFT calculations in the GGA approximation are employed. The reaction energies, activation energies and ab initio molecular dynamics of the system are calculated in a 3D periodic model, utilizing VASP.³⁰ In these calculations, the electronic energies are approximated using the projector augmented wave (PAW)³¹ description of atomic cores and the functional of Perdew, Burke, and Ernzerhof (PBE).³² The plane wave cutoff energy is set to 400 eV. For Ni atoms, 3d⁸4s² electrons are included as valence electrons. The self-consistent steps are converged to an energy difference of at least 10⁻⁴ eV. Geometries are optimized using the conjugate-gradient scheme without symmetry restraints or fixed atoms to a convergence of energy gradients of less than 10⁻³ eV Å⁻¹. Since the magnetic properties of Ni are essential for an accurate description of the energetics and kinetics,⁶ all of the calculations are spin-polarized.

To include dispersion interactions, the non-local van der Waals density functional (vdW-DF) of Langreth and Lundqvist and co-workers^33,34 has been applied. Since there is good agreement between the vdW functionals (opt), developed by Michaelides and co-workers,^35,36 and the random phase approximation (RPA) calculation,^37,38 the ‘optPBE-vdW’ has been chosen to treat the reaction energy and reaction kinetics of the adsorbed H at the Ni(111) surface.

The self-consistent electron density is performed by the iterative diagonalization of the Kohn–Sham Hamiltonian, and all total energies are calculated at zero temperature. Since crystalline atoms are usually tightly packed and the typical temperature of interest is relatively low (comparing with the melting temperature), the harmonic approximation to the transition state theory (hTST) can typically be used in studies of reactions at the crystalline surface.^39,40

The converged values of the surface energies of the Ni(111) surfaces showed that five layers of Ni are enough to be considered as a slab. To avoid the slab–slab interaction in the periodic model, a vacuum region of 10 Å above the surface is imposed. The k-point sampling in a reciprocal space is generated by the Monkhorst–Pack method. 8 × 8 × 8 and 4 × 4 × 1 grid sizes are utilized for the bulk and slab, respectively. For the surface, we use a five-layered 4 × 4 supercell, and the k-point sampling is reduced to 2 × 2 × 1. Each layer of the slab has 16 Ni atoms and is considered as a mono-layer (ML). The coverage of H-atoms is calculated based on the number of H-atoms divided by the number of Ni atoms in a ML.

In principle, H-absorption can be studied using ab initio MD (AIMD) simulations. However, H-diffusion falls into the category of rare events. This indicates that the system is trapped in some local energy minimum for a long period of time (relative to the AIMD timescale) and cannot cross the activation barrier to a new minimum.⁴¹

H-Diffusion to the subsurface is rarely observed during ab initio MD simulations at a high H-coverage, which corresponds to the reduction of activation energy of H-diffusion to the subsurface at the high H-coverage. Applying high pressure hinders H₂ desorption and keeps the H-coverage as high as possible to proceed H-absorption. Hence, if the pressure is removed, the adsorbed H-atoms intend to desorb from the surface rather than diffuse to the sub-surface and bring back the thermal equilibrium between the surface and the gas phase.

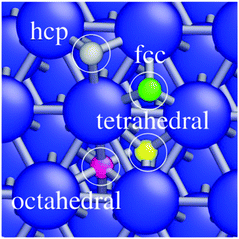
In this study, we use the nudged elastic band (NEB) method^42,43 to calculate the activation energy for reactions under different H-coverages. Since the energy minimum of the system is constantly modified by adding new H-atoms to the surface, the underlying reaction kinetics and reaction energetics of all the occurring chemical processes are constantly modified as well. In this contribution, the increase or decrease of the H-coverage generally modifies the rate of H-diffusion between the specified sites as shown in Fig. 1. This is because of the increase or decrease of the activation energy of H-diffusion between the sites. We therefore calculated the possible crossings of barriers by the NEB method and checked the activation barriers of a chemical reaction for different H-coverages.

Fig. 1 Top view of the Ni(111) surface with the adsorption sites and the subsurface interstitial sites. The hcp site and the fcc site are three coordinated (white and green atoms, respectively), while the subsurface octahedral site and the subsurface tetrahedral site are six and four coordinated (pink and yellow atoms, respectively).

The energy difference between the two optimized minima gives the reaction energy. Once the required minimum energy to cross the barrier is detected on the association or dissociation channel, this value is reported as the activation barrier. In contrast, occasionally no activation barrier is detected. In this case, we set the activation barrier to zero for an exothermic reaction and to ΔE for an endothermic reaction. In all of the calculations, all other degrees of freedom are optimized. The number of considered images is set to 10 in those reaction paths, including end images.

The vibrational frequencies of the systems are calculated within the harmonic approximation in order to include the zero point energy (ZPE) corrections. ZPE contributions are found to be essential to describe the kinetics of atomic hydrogen.⁸ The matrix of the second derivatives of the energy with respect to the atomic positions (Hessian matrix) is calculated numerically by displacing each atom twice (±0.015 Å) independently from its equilibrium position in the direction of each Cartesian coordinate. The H-atoms in a chemical reaction and their first metal neighbour atoms are included in frequency calculations, accounting for the adsorbate–metal coupling.

Results and discussion

Associative desorption of H₂ and dissociative adsorption of H₂

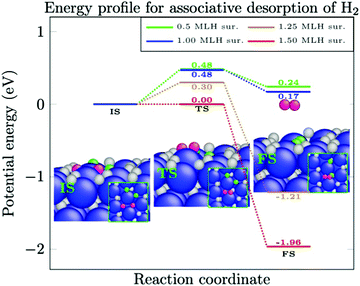
Associative desorption of H₂ from the crystalline Ni(111) surface (or the reverse process, dissociative adsorption of H₂ molecules) is examined in two different channels. In the first channel, two H-atoms are located in fcc and hcp sites that are adjacent to each other (pink atoms in the small insets of Fig. 2). The activation energy for associative desorption of the H₂ molecule is calculated for different H-coverages. We find that as the H-coverage increases, the activation energy for associative desorption of H₂ decreases. As tabulated in Table 1, up to a mono-layer of H-atoms, the activation energy does not reduce below 0.48 eV and the desorption of the H₂ molecule remains an endothermic reaction. However, an abrupt change in the reaction energy is observed when H-coverage is larger than 1.00 ML. The activation energy of the associative desorption of H₂ is reduced from 0.48 eV at a H-coverage of 1.00 ML to 0.30 eV at a H-coverage of 1.25 ML and to 0.00 eV at a H-coverage of 1.50 ML. Moreover, at these coverages, the associative desorption of H₂ becomes an exothermic reaction.

Fig. 2 Reduction in activation energy for associative desorption of H₂ upon increasing H-coverage. The side view and top view show the recombination of surface-bound H-atoms (pink atoms) to form H₂ for a H-coverage of 1.50 ML. The associative desorption of H₂ will cause H-diffusion at the surface (green atoms). The labels IS, TS and FS represent the initial state, transition state, and final state, respectively, corresponding to the red line. The IS is taken as the reference energy. The dark blue spheres represent Ni and the small white spheres represent H.

Table 1 Activation energy (E_a) and reaction energy (ΔE) for associative desorption of H₂, for different H-coverages and both H-atoms located at the fcc and hcp sites adjacent to each other

Reaction		H-Coverage (ML)	E a (eV)	ΔE (eV)
(1)	H^(hcp)(s) + H^(fcc)(s) → H2(g)	0.25	0.69	+0.60
(2)	H^(hcp)(s) + H^(fcc)(s) → H2(g)	0.50	0.48	+0.24
(3)	H^(hcp)(s) + H^(fcc)(s) → H2(g)	0.75	0.56	+0.29
(4)	H^(hcp)(s) + H^(fcc)(s) → H2(g)	1.00	0.48	+0.17
(5)	H^(hcp)(s) + H^(fcc)(s) → H2(g)	1.25	0.30	−1.21
(6)	H^(hcp)(s) + H^(fcc)(s) → H2(g)	1.50	0.00	−1.96

---

The equivalent of the associative desorption of H₂ is the dissociative adsorption of this molecule. The H-coverage in Table 1 indicates the initial coverage of H. Hence, when the reverse reaction (dissociative adsorption) is considered, 0.125 ML of H should be subtracted from this value. This indicates that H₂ from the gas phase dissociates upon adsorption on the surface, and the H-coverage increases by 0.125 ML of H. As depicted in Fig. 2, for up to 1.00 ML of H, H₂ easily dissociates at the Ni(111) surface, while at larger H-coverages, a significant amount of energy is required to dissociate the next H₂ molecule. For instance, an activation energy of 1.51 eV is required through this reaction pathway to dissociate H₂ from the gas phase to the crystalline Ni(111) surface with a H-coverage of 1.125 ML. Furthermore, this reaction is endothermic by 1.21 eV (the reverse of reaction (5), Table 1).

In the second channel, two H-atoms are located in fcc and hcp sites that are opposite to each other (Fig. 3). As tabulated in Table 2, the same reductions in activation energies of the associative desorption of H₂ are observed. This reaction becomes exothermic at 1.00 ML to 1.50 ML (see Table 2). Note that for all coverages, a larger activation energy is calculated in the second channel compared to the first channel. This indicates that the first channel is chemically more active to the associative desorption of H₂ or, vice versa, that the dissociative adsorption of H₂ is more active in the second channel, irrespective of the surface coverage.

Fig. 3 Top view of associative desorption of H₂ at a H-coverage of 1.5 ML. H-Atoms are indicated by the pink atoms. (a) Initial configuration. (b) Transition state. (c) Associative desorption of H₂. Desorption of H₂ will relocate the pre-adsorbed atomic H at the surface (green atom).

Table 2 Activation energy (E_a) and reaction energy (ΔE) for associative desorption of H₂, for different H-coverages and both H-atoms located at fcc and hcp sites opposite to each other

Reaction		H-Coverage (ML)	E a (eV)	ΔE (eV)
(1)	H^(hcp)(s) + H^(fcc)(s) → H2(g)	0.125	0.78	+0.75
(2)	H^(hcp)(s) + H^(fcc)(s) → H2(g)	0.25	0.87	+0.74
(3)	H^(hcp)(s) + H^(fcc)(s) → H2(g)	0.50	0.70	+0.68
(4)	H^(hcp)(s) + H^(fcc)(s) → H2(g)	0.75	0.94	+0.78
(5)	H^(hcp)(s) + H^(fcc)(s) → H2(g)	1.00	0.57	−0.42
(6)	H^(hcp)(s) + H^(fcc)(s) → H2(g)	1.25	0.31	−0.25
(7)	H^(hcp)(s) + H^(fcc)(s) → H2(g)	1.50	0.19	−1.91

---

The Ni(111) surface is the most closely packed surface relative to other surfaces. With an increase in H-coverage, the Ni atoms at the surface cannot relocate H-atoms to store more H-atoms. Hence, the activation energy of H₂ desorption is reduced at a high H-coverage. This can be seen in Table 2 (reactions (5)–(7)) and Table 1 (reactions (4)–(6)).

Hence, the dissociative adsorption of H₂ at a crystalline Ni(111) surface proceeds rapidly up to a H-coverage of 1.00 ML. At larger H-coverages than 1.00 ML, the so-called threshold coverage, the rate of associative desorption of H₂ increases and it opens up the pre-occupied sites for the next dissociation of an incoming H₂ molecule. Therefore, the crystalline Ni(111) surface will ultimately reach a thermodynamic equilibrium with the gas phase and the rate of H₂ dissociation will be equal to the rate of H₂ desorption, with a specific amount of surface-bound H-atoms. This amount will be different according to the type of metals, crystal planes, and applied pressures and temperatures. The H-coverage, in turn, governs the reaction kinetics as recently demonstrated.¹⁹

Dissolution of surface-bound H-atoms

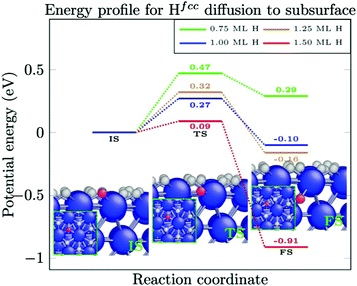
To investigate the dissolution of surface-bound H-atoms in the metal, the activation energy and reaction energy for diffusion of a surface-bound H-atom from an fcc site to the subsurface octahedral site is calculated. As listed in Table 3 (reactions (1)–(3)), we find a relatively large activation energy (>0.47 eV) at low H-coverages (up to 0.75 ML), which is in good agreement with previous calculations.^44–46 For instance, an activation energy of 0.64 eV is obtained for a H-coverage of 0.50 ML. In this condition, the H-atom can easily resurface with a small energy barrier of 0.05 eV. Henkelman et al. calculated energy barriers of 0.6 eV and 0.1 eV for H-diffusion to the subsurface and the resurfacing of H, respectively, while Ledentu et al. calculated these energy barriers to be 0.47 and 0.27 eV. Moreover, this diffusion to the subsurface is endothermic at this coverage (see Table 3). However, as depicted in Fig. 4 and Table 3 (reactions (4) and (5)), upon increasing the H-coverage, diffusion of surface-bound H-atoms to the subsurface becomes an exothermic reaction. This is accompanied by a reduction in activation energy. For instance, an activation energy of 0.09 eV is calculated for a H-coverage of 1.50 ML (Table 3, reaction (6)). At this coverage, H-atoms can hardly resurface with a large energy barrier of 1.00 eV.

Table 3 Activation energy (E_a) and reaction energy (ΔE) for H-diffusion to a subsurface octahedral (H^sub.oct) or tetrahedral (H^sub.tet) site, for different H-coverages (at the surface or subsurface)

Reaction		H-Coverage	E a (eV)	ΔE (eV)
(1)	H^(fcc)(s) → H^(sub.oct.)(s)	0.25 ML	0.47	+0.32
(2)	H^(fcc)(s) → H^(sub.oct.)(s)	0.50 ML	0.64	+0.59
(3)	H^(fcc)(s) → H^(sub.oct.)(s)	0.75 ML	0.47	+0.29
(4)	H^(fcc)(s) → H^(sub.oct.)(s)	1.00 ML	0.27	−0.10
(5)	H^(fcc)(s) → H^(sub.oct.)(s)	1.25 ML	0.32	−0.16
(6)	H^(fcc)(s) → H^(sub.oct.)(s)	1.50 ML	0.09	−0.91
(7)	H^(fcc)(s) → H^(sub.oct.)(s)	1.44 ML and 0.06 subML	0.13	−0.85
(8)	H^(fcc)(s) → H^(sub.oct.)(s)	1.38 ML and 0.12 subML	0.13	−0.75
(9)	H^(hcp)(s) → H^(sub.tet.)(s)	1.50 ML	0.10	−0.66
(10)	H^(hcp)(s) → H^(sub.tet.)(s)	1.44 ML and 0.06 subML	0.15	−0.43
(11)	H^(hcp)(s) → H^(sub.tet.)(s)	1.38 ML and 0.12 subML	0.14	−0.49

---

Fig. 4 Reduction in activation energy for H-diffusion to the subsurface upon increasing H-coverage. A higher H-coverage facilitates H-diffusion (pink atom) from an fcc site to a subsurface octahedral site. The insets correspond to the red line.

In the following, further diffusion of H-atoms to the subsurface at a high H-coverage is explored. When the H-atoms already occupy a subsurface site, the activation energy for the second and third diffusion events from an fcc site to a subsurface octahedral site is calculated to be 0.13 eV (Table 3, reactions (7) and (8)). In this situation, a subsurface H-atom requires large energy barriers of 0.98 eV and 0.88 eV to resurface, respectively. Similar calculations have been performed for the diffusion of a surface-bound H-atom from a hcp site to the subsurface tetrahedral site. As listed in Table 3 (reactions (9)–(11)), low activation barriers are calculated for H-diffusion to the subsurface. When H-atoms occupy some subsurface sites, the activation energy increases slightly from 0.10 eV to 0.15 eV and to 0.14 eV for the first, second, and third diffusion events, respectively. When the surface H-coverage reduces, H-diffusion to the subsurface becomes slightly less exothermic.

If a high-pressure hydrogen source is applied, the flux of H-atoms to the surface will be high. This results in a high coverage of H-atoms at the surface. As the H-coverage increases, depending on the stiffness of the crystal plane of the metal, surface-bound H-atoms can dissolve and diffuse into the bulk of the metal.

To investigate to what extent H-diffusion proceeds into the bulk, diffusion of H-atoms from the subsurface sites to the sites below the second layer of the crystalline Ni(111) surface (i.e., to the sub-subsurface) is calculated. As tabulated in Table 4, initially, a surface coverage of 1.50 ML of H and a subsurface coverage of 0.06 ML of H are considered. The activation energies of 0.27 eV and 0.32 eV are calculated for diffusion of a subsurface H-atom from the subsurface octahedral site and the subsurface tetrahedral site to the sub-subsurface tetrahedral site and the sub-subsurface octahedral site, respectively. The first process is found to be slightly exothermic, while the second process is endothermic.

Table 4 Activation energy (E_a) and reaction energy (ΔE) for H-diffusion from the subsurface to the sub-subsurface, for a surface H-coverage of 1.50 ML, and different H-coverages at the subsurface (subsurface octahedral = sub.oct., subsurface tetrahedral = sub.tet., sub-subsurface tetrahedral = sub.sub.tet., and sub-subsurface octahedral = sub.sub.oct.)

Reaction		H-Coverage	E a (eV)	ΔE (eV)
(1)	H^(sub.oct.)(s) → H^(sub.sub.tet.)(s)	1.50 ML and 0.06 subML	0.27	−0.06
(2)	H^(sub.tet.)(s) → H^(sub.sub.oct.)(s)	1.50 ML and 0.06 subML	0.32	+0.26
(3)	H^(sub.oct.)(s) → H^(sub.sub.tet.)(s)	1.50 ML and 1.00 subML	0.44	+0.07
(4)	H^(sub.tet.)(s) → H^(sub.sub.oct.)(s)	1.50 ML and 1.00 subML	0.55	+0.51
(5)	H^(sub.oct.)(s) → H^(sub.sub.tet.)(s)	1.50 ML and 1.25 subML	0.10	−0.56
(6)	H^(sub.tet.)(s) → H^(sub.sub.oct.)(s)	1.50 ML and 1.25 subML	0.28	+0.05
(7)	H^(sub.tet.)(s) → H^(sub.tet.)(s)	1.44 ML and 0.06 subML	0.00	−0.16
(8)	H^(sub.tet.)(s) → H^(sub.oct.)(s)	1.44 ML and 0.06 subML	0.14	−0.14
(9)	H^(sub.tet.)(s) → H^(sub.oct.)(s)	1.44 ML and 0.06 subML	0.09	−0.12

---

The same calculations have been performed for a surface coverage of 1.50 ML of H and a subsurface coverage of 1.00 ML of H and 1.25 ML of H (Table 4, reactions (3)–(6)). As the H-coverage at the subsurface increases to 1.00 ML, the activation energies rise to 0.44 eV and 0.55 eV, respectively. Moreover, both reactions now become endothermic (Table 4, reactions (3) and (4)). When the subsurface H-coverage is 1.25 ML, the corresponding activation energies are reduced to 0.10 eV and 0.28 eV. Reaction (5) is now exothermic and the H-atoms in the sub-subsurface sites can hardly go back to the subsurface due to a large activation energy of 0.66 eV, while reaction (6) is slightly endothermic by 0.05 eV. Thus, once the interstitial H-coverage of the subsurface is higher than 1.00 ML, the dissolution of H-atoms to the sub-subsurface will be initiated.

Hence, diffusion of H-atoms to the bulk of the crystalline Ni(111) surface rarely happens until the interstitial H-coverage passes the threshold of 1.00 ML in each interstitial space. This can be induced by increasing the pressure and temperature. The increase of pressure may give rise to a complete phase transition from metal to metal hydride or filling up the interstitial sites to some extent. Clearly, if pressure is reduced, the stored interstitial H-atoms can easily go back to the surface and produce an abundant amount of H₂ by associative desorption (see the first section).

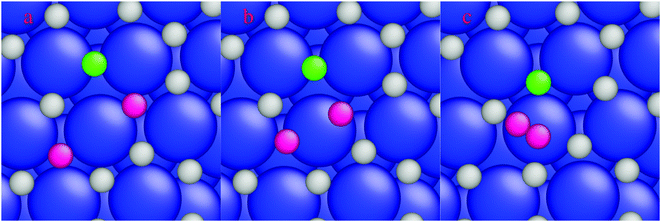
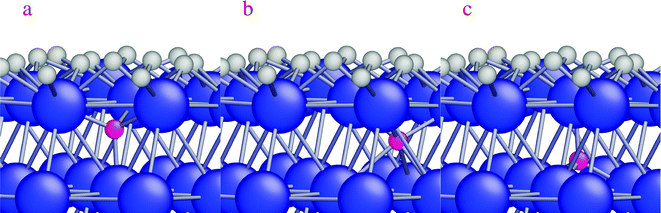
A higher temperature increases the diffusion of dissolved H-atoms in the bulk between the interstitial sites. After diffusion of surface H-atoms from the hcp site to the subsurface tetrahedral site, the limited space below the hcp site (Fig. 5a) causes the diffusing H-atom to diffuse to either the subsurface octahedral site or the subsurface tetrahedral site (Fig. 5b and c, respectively). The activation and reaction energies for interstitial diffusion between the subsurface sites are listed in Table 4 (reactions (7)–(9)). H-diffusion becomes a barrierless reaction for H-diffusion from a subsurface tetrahedral to another subsurface tetrahedral site (Table 4, reaction (7)). An activation energy of 0.14 eV is calculated for diffusion to a subsurface octahedral site. The reaction is slightly exothermic by 0.14 eV and the reverse diffusion has an activation barrier of 0.28 eV (Table 4, reaction (8)). The last reaction in Table 4 shows the interstitial diffusion between a subsurface tetrahedral site and a subsurface octahedral site. A small activation energy of 0.09 eV is calculated for the interstitial diffusion, which shows that H-atoms in the interstitial space between layers are highly mobile.

Fig. 5 Side view of H-diffusion to the sub-subsurface. (a) The H-atom in the subsurface tetrahedral site is indicated by the pink atoms. (b) The H-atom is located in the sub-subsurface octahedral site (six coordinated). (c) The H-atom is located in the sub-subsurface tetrahedral site (four coordinated).

Application to plasma catalysis

In a thermal process, the applied pressure, depending on the type of metal and the crystalline surface, produces a certain coverage of surface-bound H-atoms. Therefore, depending on the partial pressure of the H-source, the interstitial sites are filled up to some extent. In contrast to a thermal process, a plasma process typically operates at atmospheric pressure (or below) and at room temperature (or slightly above). In this case, energetic electrons, existing in the plasma with a typical energy of 1–10 eV, create the reactive species (free radicals, excited molecules, and ions). Therefore, the threshold coverage of some selected species (e.g. H-atoms) can easily be achieved by a strong adsorption of the reactive species. This was observed experimentally by Jiang et al.⁴⁷ for a crystalline Pd(111) surface. As a result, a higher number of H-atoms will cover the surface at a reduced temperature as compared to thermal catalysis. As we have demonstrated recently, this in turn reduces the activation barrier for many catalytic reactions at the Ni(111) surface.

Therefore, depending on the ability and efficiency of the plasma for the formation of reactive species (e.g. H-atoms), the interstitial sites can be replenished by H-atoms. As a higher H-coverage can be more easily achieved by a plasma than by a thermal catalytic process, the plasma-assisted catalytic hydrogenation should be more efficient than the thermal catalytic hydrogenation.

Conclusions

We employed atomistic simulations at the DFT level to investigate the diffusion of H-atoms from a crystalline Ni(111) surface to the subsurface and further into the bulk, in the context of thermal catalytic and plasma-assisted catalytic processes. The H-atoms at the surface can originate from dissociative adsorption of H₂ or CH₄ molecules, or, in the plasma-assisted case, from their generation in the plasma phase. Dissociative adsorption of H₂ readily occurs at a bare Ni(111) surface. When increasing the H-coverage to 1.00 ML, the so-called threshold coverage, dissociative adsorption of H₂ becomes endothermic and thus unfavourable. In this case, associative desorption of H₂ or the consumption of surface-bound H-atoms by another reactant should first release the reactive sites for the further dissociative adsorption of H₂.

A higher or lower partial pressure of the hydrogen source will shift the H-coverage up and down, respectively. When the threshold H-coverage is passed (i.e., 1.00 ML for the crystalline Ni(111) surface), the high applied pressure will result in the diffusion of surface-bound H-atoms to the subsurface. The extent of the dissolution of H-atoms depends largely on the applied pressure and temperature. A similar threshold coverage is observed for the interstitial H-coverage. Once the interstitial sites are filled up with a coverage of above 1.00 ML of H, dissolution of interstitial H-atoms to the layer below the interstitial sites will be initiated. A higher temperature facilitates H-diffusion in the interstitial space between the Ni(111) layers (planar diffusion) and H-diffusion between the interstitial spaces (vertical diffusion). Hence, by applying a high pressure and high temperature, a significant amount of hydrogen can be stored in a crystalline metal like Ni. Equivalently, the stored H-atoms in the bulk can easily go back to the surface and release a large amount of heat. Through the reverse reaction, molecular hydrogen can either associatively desorb from the surface and produce an abundant amount of H₂ or be consumed by another reactant in a catalytic reaction.

We showed before that catalytic hydrogenation reactions proceed faster in the presence of a high H-coverage. This indicates that the hydrogenation of molecular fragments of added value chemicals is facilitated under conditions of a high H-coverage. However, the facilitative hydrogenation of molecular fragments to the reactants occurs as well. Hence, the overall rate of conversion should be the same. However, here, we show that the H-absorption hinders the reverse reactions to the reactants and shifts the equilibrium to the side of the product.

In a plasma process, there is an increased flow of H-atoms that can readily adsorb at the surface and achieve the threshold coverage without applying a high pressure as in a thermal process. As a result, depending on the crystal planes and type of metals, a large amount of H-atoms can be dissolved in the metal catalyst, explaining the high efficiency of plasma-assisted catalytic reactions.

Acknowledgements

Financial support from the Reactive Atmospheric Plasma processIng – eDucation (RAPID) network, through the EU 7th Framework Programme (grant agreement no. 606889), is gratefully acknowledged. The calculations were performed using the Turing HPC infrastructure at the CalcUA core facility of the Universiteit Antwerpen, a division of the Flemish Supercomputer Center VSC, funded by the Hercules Foundation, the Flemish Government department (EWI) and the Universiteit Antwerpen.

References

1. J. Völkl and G. Alefeld, in Diffusion of hydrogen in metals, ed. G. Alefeld and J. Völkl, Hydrogen in Metals I: Basic Properties, Springer Berlin Heidelberg, Berlin, Heidelberg, 1978, pp. 321–348.
2. S. T. Ceyer, The Unique Chemistry of Hydrogen beneath the Surface: Catalytic Hydrogenation of Hydrocarbons, Acc. Chem. Res., 2001, 34, 737–744.
3. A. D. Johnson, S. P. Daley, A. L. Utz and S. T. Ceyer, Chemistry of Bulk Hydrogen: Reaction of Hydrogen Embedded in Nickel with Adsorbed CH₃, Science, 1992, 257, 223–225.
4. S. P. Daley, A. L. Utz, T. R. Trautman and S. T. Ceyer, Ethylene Hydrogenation on Ni(111) by Bulk Hydrogen, J. Am. Chem. Soc., 1994, 116, 6001–6002.
5. B. Hammer and J. K. Norskov, Why gold is the noblest of all the metals, Nature, 1995, 376, 238–240.
6. G. Kresse and J. Hafner, First-principles study of the adsorption of atomic H on Ni(111), (100) and (110), Surf. Sci., 2000, 459, 287–302.
7. J. E. Mueller, A. C. T. van Duin and W. A. Goddard, Competing, Coverage-Dependent Decomposition Pathways for C2Hy Species on Nickel(111), J. Phys. Chem. C, 2010, 114, 20028–20041.
8. T. Vegge, Locating the rate-limiting step for the interaction of hydrogen with Mg(0001) using density-functional theory calculations and rate theory, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 70, 035412.
9. X.-Q. Zhang, R. A. van Santen and E. J. M. Hensen, Carbon-Induced Surface Transformations of Cobalt, ACS Catal., 2015, 5, 596–601.
10. J. P. Van Hook, Methane-Steam Reforming, Catal. Rev., 1980, 21, 1–51.
11. D. Pakhare and J. Spivey, A review of dry (CO₂) reforming of methane over noble metal catalysts, Chem. Soc. Rev., 2014, 43, 7813–7837.
12. X. Tu and J. C. Whitehead, Plasma-catalytic dry reforming of methane in an atmospheric dielectric barrier discharge: Understanding the synergistic effect at low temperature, Appl. Catal., B, 2012, 125, 439–448.
13. E. C. Neyts, K. Ostrikov, M. K. Sunkara and A. Bogaerts, Plasma Catalysis: Synergistic Effects at the Nanoscale, Chem. Rev., 2015, 115, 13408–13446.
14. A. Fridman, Plasma Chemistry, Cambridge University Press, 2008.
15. A. Bogaerts, T. Kozak, K. van Laer and R. Snoeckx, Plasma-based conversion of CO₂: current status and future challenges, Faraday Discuss., 2015, 183, 217–232.
16. B. Hammer and J. K. Nørskov, Theoretical surface science and catalysis—calculations and concepts, Advances in Catalysis, Academic Press, 2000, pp. 71–129.
17. S. Furukawa, K. Ehara, K. Ozawa and T. Komatsu, A study on the hydrogen activation properties of Ni-based intermetallics: a relationship between reactivity and the electronic state, Phys. Chem. Chem. Phys., 2014, 16, 19828–19831.
18. F. A. Lewis, Solubility of hydrogen in metals, Pure Appl. Chem., 1990, 62, 6.
19. M. Shirazi, E. C. Neyts and A. Bogaerts, DFT study of Ni-catalyzed plasma dry reforming of methane, Appl. Catal., B, 2017, 205, 605–614.
20. M. Shirazi and S. D. Elliott, Atomistic kinetic Monte Carlo study of atomic layer deposition derived from density functional theory, J. Comput. Chem., 2014, 35, 244–259.
21. H. M. Cuppen, L. J. Karssemeijer and T. Lamberts, The Kinetic Monte Carlo Method as a Way To Solve the Master Equation for Interstellar Grain Chemistry, Chem. Rev., 2013, 113, 8840–8871.
22. X. Q. Zhang, W. K. Offermans, R. A. van Santen, A. P. J. Jansen, A. Scheibe, U. Lins and R. Imbihl, Frozen thermal fluctuations in adsorbate-induced step restructuring, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 113401.
23. X.-Q. Zhang, T. T. Trinh, R. A. van Santen and A. P. J. Jansen, Mechanism of the Initial Stage of Silicate Oligomerization, J. Am. Chem. Soc., 2011, 133, 6613–6625.
24. A. W. C. van den Berg and C. O. Arean, Materials for hydrogen storage: current research trends and perspectives, Chem. Commun., 2008, 668–681.
25. Y.-H. Huang, R. I. Dass, Z.-L. Xing and J. B. Goodenough, Double Perovskites as Anode Materials for Solid-Oxide Fuel Cells, Science, 2006, 312, 254–257.
26. J. N. Huiberts, R. Griessen, J. H. Rector, R. J. Wijngaarden, J. P. Dekker, D. G. de Groot and N. J. Koeman, Yttrium and lanthanum hydride films with switchable optical properties, Nature, 1996, 380, 231–234.
27. S. D. Elliott, G. Dey, Y. Maimaiti, H. Ablat, E. A. Filatova and G. N. Fomengia, Modeling Mechanism and Growth Reactions for New Nanofabrication Processes by Atomic Layer Deposition, Adv. Mater., 2016, 28, 5367–5380.
28. E. C. Neyts, Y. Shibuta, A. C. T. van Duin and A. Bogaerts, Catalyzed Growth of Carbon Nanotube with Definable Chirality by Hybrid Molecular Dynamics–Force Biased Monte Carlo Simulations, ACS Nano, 2010, 4, 6665–6672.
29. W. Grochala and P. P. Edwards, Thermal Decomposition of the Non-Interstitial Hydrides for the Storage and Production of Hydrogen, Chem. Rev., 2004, 104, 1283–1316.
30. G. Kresse and J. Hafner, Ab initio molecular dynamics for liquid metals, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 558–561.
31. P. E. Blöchl, Projector augmented-wave method, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979.
32. J. P. Perdew, K. Burke and M. Ernzerhof, Generalized Gradient Approximation Made Simple, Phys. Rev. Lett., 1996, 77, 3865–3868.
33. M. Dion, H. Rydberg, E. Schröder, D. C. Langreth and B. I. Lundqvist, van der Waals Density Functional for General Geometries, Phys. Rev. Lett., 2004, 92, 246401.
34. K. Lee, É. D. Murray, L. Kong, B. I. Lundqvist and D. C. Langreth, Higher-accuracy van der Waals density functional, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 081101.
35. J. Klimeš, D. R. Bowler and A. Michaelides, van der Waals density functionals applied to solids, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83, 195131.
36. K. Jiří, R. B. David and M. Angelos, Chemical accuracy for the van der Waals density functional, J. Phys.: Condens. Matter, 2010, 22, 022201.
37. F. Mittendorfer, A. Garhofer, J. Redinger, J. Klimeš, J. Harl and G. Kresse, Graphene on Ni(111): Strong interaction and weak adsorption, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 201401.
38. J. Harl and G. Kresse, Accurate Bulk Properties from Approximate Many-Body Techniques, Phys. Rev. Lett., 2009, 103, 056401.
39. A. F. Voter and J. D. Doll, Dynamical corrections to transition state theory for multistate systems: Surface self-diffusion in the rare-event regime, J. Chem. Phys., 1985, 82, 80–92.
40. P. Hänggi, P. Talkner and M. Borkovec, Reaction-rate theory: fifty years after Kramers, Rev. Mod. Phys., 1990, 62, 251–341.
41. K. M. Bal and E. C. Neyts, Merging Metadynamics into Hyperdynamics: Accelerated Molecular Simulations Reaching Time Scales from Microseconds to Seconds, J. Chem. Theory Comput., 2015, 11, 4545–4554.
42. G. Henkelman, B. P. Uberuaga and H. Jónsson, A climbing image nudged elastic band method for finding saddle points and minimum energy paths, J. Chem. Phys., 2000, 113, 9901–9904.
43. H. Jónsson, Simulation of surface processes, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 944–949.
44. G. Henkelman, A. Arnaldsson and H. Jónsson, Theoretical calculations of CH₄ and H₂ associative desorption from Ni(111): Could subsurface hydrogen play an important role?, J. Chem. Phys., 2006, 124, 044706.
45. A. Michaelides, P. Hu and A. Alavi, Physical origin of the high reactivity of subsurface hydrogen in catalytic hydrogenation, J. Chem. Phys., 1999, 111, 1343–1345.
46. V. Ledentu, W. Dong and P. Sautet, Heterogeneous Catalysis through Subsurface Sites, J. Am. Chem. Soc., 2000, 122, 1796–1801.
47. J. Z. Null, H. W. Null and B. X. null, Interaction of gas phase atomic hydrogen with Pt(111): direct evidence for the formation of bulk hydrogen species, Sci. China, Ser. B: Chem., 2007, 50, 91.

---

Footnote

† Eindhoven University of Technology, Department of Applied Physics, P.O. Box 513, 5600 MB Eindhoven, The Netherlands. E-mail: m.shirazi@tue.nl

---