Imaging Aβ(1–42) fibril elongation reveals strongly polarised growth and growth incompetent states†
Abstract
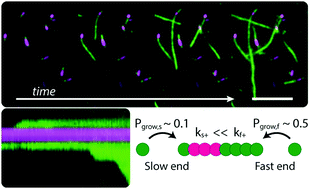
The major hallmark of Alzheimer's disease is the deposition of plaques of amyloid fibrils formed from amyloid-β (Aβ) peptides. Kinetic studies have contributed significantly towards a mechanistic understanding of amyloid fibril self-assembly, however dynamic features of the aggregation process cannot be captured using ensemble methods. Here we present an assay for imaging Aβ42 aggregation dynamics at the single fibril level, allowing for the quantitative extraction of concentration and temperature dependent kinetic parameters. From direct observation of elongation using TIRF and super-resolution optical microscopy, we find that Aβ42 fibril growth is strongly polarized, with fast and slow growing ends arising from different elongation rates, but also from a growth incompetent state, which dominates the process at the slow growing end. Our findings reveal the surprising complexity of the Aβ42 fibril elongation reaction at the microscopic level.
- This article is part of the themed collection: 2017 PCCP HOT Articles


 Please wait while we load your content...
Please wait while we load your content...