Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Unidirectional motion of a camphor disk on water forced by interactions between surface camphor concentration and dynamically changing boundaries†
Jerzy
Gorecki
 *a,
Hiroyuki
Kitahata
*a,
Hiroyuki
Kitahata
 b,
Nobuhiko J.
Suematsu
b,
Nobuhiko J.
Suematsu
 c,
Yuki
Koyano
c,
Yuki
Koyano
 d,
Paulina
Skrobanska
d,
Paulina
Skrobanska
 a,
Marian
Gryciuk
a,
Marian
Gryciuk
 a,
Maciej
Malecki
a,
Maciej
Malecki
 a,
Takahiro
Tanabe
d,
Hiroya
Yamamoto
d and
Satoshi
Nakata
a,
Takahiro
Tanabe
d,
Hiroya
Yamamoto
d and
Satoshi
Nakata
 d
d
aInstitute of Physical Chemistry, Polish Academy of Sciences, Kasprzaka 44/52, 01-224 Warsaw, Poland. E-mail: jgorecki@ichf.edu.pl
bDepartment of Physics, Chiba University, 1-33 Yayoi-cho, Inage-ku, Chiba 263-8522, Japan
cGraduate School of Advanced Mathematical Sciences and Meiji Institute of Advanced Study of Mathematical Sciences, Meiji University, 4-21-1 Nakano, Tokyo 164-8525, Japan
dGraduate School of Science, Hiroshima University, 1-3-1 Kagamiyama, Higashi-Hiroshima 739-8526, Japan
First published on 26th June 2017
Abstract
We study the motion of a camphor disk on the water surface in a system with flexible boundaries. The boundaries can be dynamically modified by non-uniform surface tension resulting from the nonhomogeneous surface concentration of the camphor molecules dissipated by the disk. We investigate the geometry of the boundaries that forces unidirectional motion of the disk. The studied system can be regarded as a signal diode if the presence or absence of a camphor disk at a specific point is interpreted as the binary TRUE and FALSE variables. The diode can be incorporated into more complex devices, like a ring that imposes unidirectional rotation of camphor disks.
Introduction
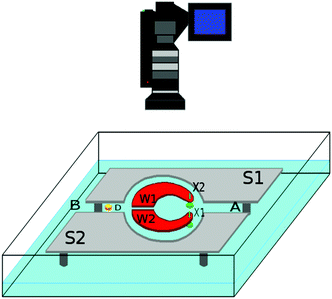
Camphor particles self-moving on the water surface have been investigated as an example of self-propelled objects for almost two centuries.1–3 The driving force for a camphor particle comes from spatial inhomogeneities in the surface tension around it. A camphor particle placed on the water surface dissipates camphor molecules. The profile of the surface camphor concentration on water results from the balance between the inflow of camphor molecules from the solid camphor, and their sublimation into the air phase and dissolution into the water phase.3 The surface tension is a decreasing function of the surface concentration of camphor molecules.4,5 As a result, the camphor particle moves in the direction of a region with a lower surface camphor concentration. There are many advantages of using camphor in experiments with self-propelled particles. Such systems allow for easy control over experimental conditions and the motility time is long.There are many studies on the influence of the water chamber shape on the complexity of the motion of camphor particles.6–8 However, most of the published results were obtained for systems with fixed, time independent chamber boundaries. The authors recall only two papers concerned with the interactions mediated by surface camphor concentrations that can dynamically change system boundaries, depending on the location of a camphor particle.9,10 In the paper of Nakata et al.9 a disk was placed inside a small ring that could float on the water surface. The system was generalized in ref. 10 and a cross-shaped camphor rotator inside a flexible floating loop composed of a cellulose string was studied. The ring and the loop were much smaller than the Petri dish where the system was placed. In both cases the coupling between the camphor particle and system boundaries (ring or loop) was observed, but the interactions did not change qualitatively the character of the camphor motion. Here (cf.Fig. 1) we consider a system with the moving boundaries in a form of a gate with swinging wings that can open or close depending on the surface camphor concentration. The geometry of the swinging wings has been selected such that they can close irreversibly, making a part of the water chamber inaccessible to the disk.
Let us consider the camphor disk as an information carrier and relate binary information to its presence (= TRUE) or absence (= FALSE) in a selected region of space at a given time.11 The idea of using camphor disks for information processing application fits into the theoretical concept of billiard-ball computing.12 In billiard-ball computing it is assumed that information carrying objects move with a constant speed without any energy losses. Information is processed through elastic collisions with a cleverly prepared geometry of walls and in elastic collisions with other objects. Such properties of a mechanical information carrier seem to be highly idealized. We think that the idea of the sustained motion of an object can be achieved if self-propelled particles are considered as information carriers. The motion of such objects is usually supported by chemical or physical processes that use the energy of the medium and transform it into the mechanical one.
The gate considered in this paper can open and transmit camphor disks in one direction and it remains closed in the other. Therefore, it can be applied as a signal diode for information coded in the presence of a camphor particle. We name it a chemo-mechanical signal diode because it opens with the large gradient of surface camphor concentration and its closed position is stabilized by the mechanical properties of plastics used. A signal diode is an important element of complex information processing devices. If the diode is placed between an input channel and the signal processing region, unwanted interferences between the input signal and the output can be stopped. The signal diode can also be used to force the required direction of information flow important for programmable gates,13 frequency filters14 and counters.15 Intensive studies on chemical signal diodes were done for information processing with an excitable Belousov–Zhabotinsky reaction.16,17 The basic construction of a chemical signal diode13,18 uses the asymmetry of the junction formed by a rectangular excitable channel on one side and a triangular excitable channel on the other. The excitable channels are separated by the gap of the non-excitable medium. For the BZ-reaction the diode functionality is based on the properties of the reaction involved, and in particular on the non-symmetrical dissipation of the reaction activator. The diodes described in ref. 13 and 18 do not involve any mechanical motion coupled with chemical processes. However, the BZ reaction,19 and other nonlinear processes,20 can lead to changes in surface tension. These changes can be used to move a nonreactive particle21 and visualize unidirectional propagation. In the case of a diode for camphor disks the water channels play the role of an excitable medium where information can propagate and the surrounding plastic sheets form non-excitable boundaries. The unidirectionality of motion is introduced by the nonsymmetrical positions of the wing axes and their specific geometries.
Experimental section
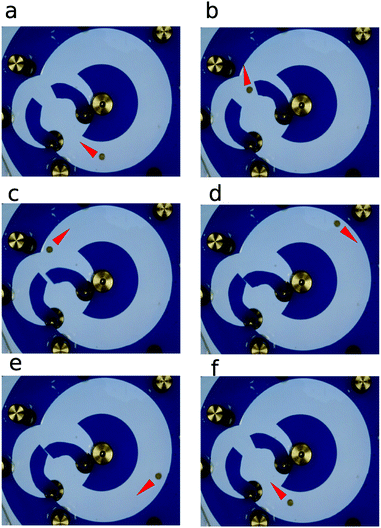
Our experiments on a gate that forces unidirectional motion of camphor disks were performed for the system illustrated in Fig. 1 except those in Fig. 5. The gate was located in a tank with distilled water (the water level: 10 mm). The grey and red areas represent polypropylene sheets reclining on the water surface. The locations of grey sheets S1 and S2 on the water surface were fixed. They defined the geometry of the water channel A–B in which information can be transmitted. The gate was located in the circular chamber in the mid of the channel. It was made of two red wings W1 and W2, which were able to rotate around fixed axes X1 and X2 marked in green. The wings could move on the water surface only. Therefore, their motion was restricted by the shape and size of the water chamber, and the position of the other wing. If both wings moved towards the boundaries of the chamber, then the gap between them was sufficiently large and a camphor disk (D) could pass through the gate. The motion of the wings and the camphor disk was digitally recorded. The camera (SONY NEX-VG20EH) was always located above the system as indicated in Fig. 1. In experiments we used commercially available camphor (99% purity, Sigma-Aldrich) without further purification. The diameter of the camphor disk was 3 mm and it was 1 mm high. The disk was made by pressing in a pill maker.Fig. 2 shows snapshots illustrating that the gate works as a chemo-mechanical diode for the signal coded in the location of a camphor disk. The disks were transmitted from right to left, but not allowed to propagate in the reverse direction. The width of the water channel was 20 mm, as indicated in Fig. 2c. The central chamber was made of two half-disks with a diameter of 20 mm. Wings W1 and W2 were made of a transparent plastic photo-copy film (STAEDTLER Lumocolor, thickness: 0.1 mm). The wing axes are marked with green dots in the centres of the black circles. There were small black dots (diameter 2 mm) glued at the opening ends of the wings used to digitize the wing motion from the recorded movie. The experiments were performed at a temperature of 24 ± 1 °C. At such temperature the dissolution rate of camphor in water is negligible (less than 2 μg s−1)5 and the dissolved camphor does not change the water density.
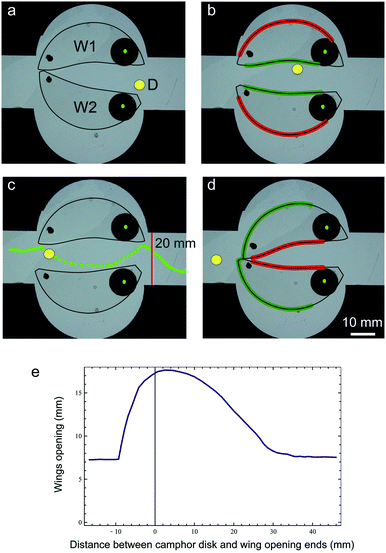 | ||
| Fig. 2 (a–d) Snapshots from a movie showing that a camphor disk (marked by a yellow disk) can open the gate and move from right to left. The interval between the snapshots was 0.5 s. Green dots inside the black circles show the positions of the rotation axes. Red and green lines indicate high and low surface tensions, respectively. The dark blue coloured regions in (a–d) correspond to the sheets defining the channel. The green squares in (c) mark the trajectory of the disk when it passes through the gate. The same trajectory is illustrated in Fig. 4a. (e) Wing opening as a function of the distance between the camphor disk and wing opening ends. | ||
The camphor disk dissipates molecules on the water surface, but they continuously sublimate. Therefore, the surface concentration of camphor close to the disk is higher than that away from it. If the disk is near the wings, the surface concentration of camphor on the edge of the wing close to the disk is larger than on the other edges, because the wing obstructs the surface motion of camphor molecules. The surface tension of water is a decreasing function of the surface concentration of camphor.3 For pure water it is 72 mN m−1, whereas for the maximum concentration of dissolved camphor it decreases to 55 mN m−1.22 Such a significant change is sufficient to move objects on the water surface. A wing is attracted to the regions where the surface concentration of camphor is small. In Fig. 2b and d, the wing boundaries experiencing high and low surface tension are marked with red and green lines, respectively. In Fig. 2a, the disk is located on the right side of the gate. It is far away from the opening ends of the wings and the surface diffusion of camphor has little influence on wing positions. Fig. 2b illustrates the response of the wings to the disk that entered the gate by 15 mm. The surface concentration of camphor in between the wings was higher than that on the other side of the wings. Therefore, the water surface tension in between the wings was lower (green line) than close to the chamber boundaries (red line). Direct measurement with a platinum wire (diameter 0.5 mm) as a Wilhelmy plate gives 65 mN m−1 close to the boundary marked with the green line and a value similar to the surface tension of pure water close to the red line.23 As a result, the wings were attracted towards the chamber boundary and the gate opened. If the diameter of the central chamber is large, then the gate can open wide enough to pass the camphor disk (cf.Fig. 2c). After opening, the disk spontaneously moved toward the left part of the channel, where the surface concentration of camphor was low. When the disk passed to the other side of the gate, the surface concentration of camphor in the left side of the gate became high. On the other hand, the surface concentration inside the gate decreased because of camphor sublimation. As indicated in Fig. 2d, the regions of high and low surface tension reversed when compared to Fig. 2b. Now the wings were pushed towards each other and mechanically closed the gate. The wings remained closed any time the camphor disk appeared on the left side. The disk motion in the direction from left to right was blocked. The opening of the wings, measured as the distance between the black dots marking the wing opening ends, as a function of the distance between the camphor disk and the midpoint between the dots is shown in Fig. 2e. The black dots were placed a bit away from the opening ends and the distance between them was 7 mm when the gate was closed.
We performed a number of experiments with the gate illustrated in Fig. 1 and a few (up to 5) camphor disks. If the disks were placed in the B region (cf.Fig. 1), then the wings never opened. If they were initially placed in the A region, then the gate opened just after the first disk got close to the wings, and the disks moved to the B region. If there were disks in both A and B regions, then a disk from the A region could open the gate and the transition against the diode direction could occur. However, after some time all disks grouped in the B region. An example of such evolution is attached as Movie (si1.avi) in the ESI.†
Numerical simulations of gate opening
Our model for the numerical calculation of the chemo-mechanical signal diode returns the time dependent position of the camphor disk centre, rc(t), and the angles, ϕ1(t) and ϕ2(t), describing the positions of both wings with respect to the symmetry axis of the channel, together with the surface concentration of camphor c(t, x, y).3,24,25 The time evolution of c(t, x, y) is calculated from the equation: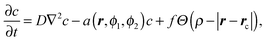 | (1) |
The position of the camphor particle can be calculated from the following Newton's equation of motion:
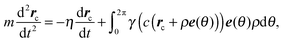 | (2) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ, sin
θ, sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ), and γ(c) is the relation between the surface tension γ and camphor concentration c. As the simplest approximation, we assumed that
θ), and γ(c) is the relation between the surface tension γ and camphor concentration c. As the simplest approximation, we assumed that| γ(c) = γ0 − kc | (3) |
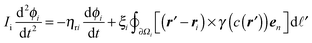 | (4) |
We adopt the Neumann boundary conditions for eqn (1) at the periphery of the water surface in a sufficiently long rectangular channel and a circular chamber. Initially, a camphor disk is located near one end of the rectangular chamber, so that the camphor disk starts to move to the gate. In order to avoid collisions between a wing and the chamber boundary, between the wings, or between the camphor disk and a wing, we detect the possible overlap and set normal velocities to zero. The numerical calculation was performed using the Euler method with a time step of Δt = 10−4, and a spatial unit of Δx = 0.025. The configuration used in the simulation is depicted in Fig. 3. We found that the camphor disk passes through in one direction, but it does not pass in the opposite one. The simulated time evolution of the gate is attached as a Movie (si2.mpg) in the ESI.†
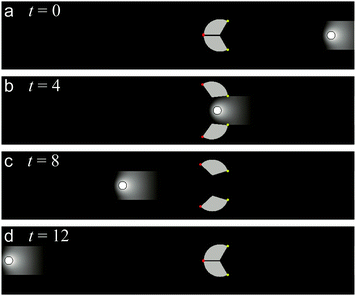 | ||
| Fig. 3 Numerical results showing that a camphor disk (white disk) can open the gate and move from right to left. The position of the disk together with the profile of the surface camphor concentration is illustrated. The gate wings are formed by a circular sector with a central angle of 2π/3 and a radius of 1. The yellow dots mark the positions of the wing axes. The red dots show the moving ends of the wings (cf.Fig. 4). The radii of the half-disks making the central chamber were 1.1. The snapshot times are given in the figures. | ||
The qualitative agreement between experiments and simulations is illustrated in Fig. 4. It shows superimposed locations of the disk centre (D) and marks at the opening ends of wings W1 and W2. The time corresponding to a given disk–wing configuration is the value of the z-variable and it is indicated as a coloured point, from red to blue.
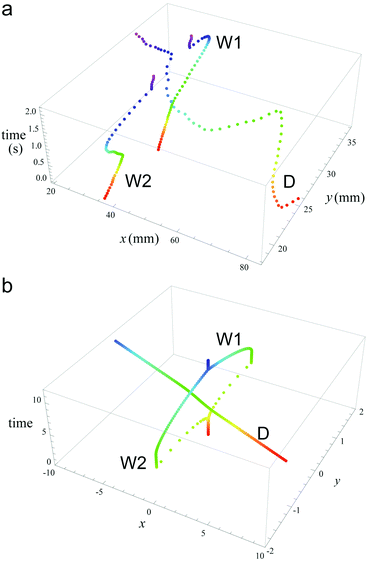 | ||
| Fig. 4 Superimposed location of the disk centre (D) and marks on wings W1 and W2. Figure (a) shows the experimental results. A similar behaviour was obtained in numerical simulations (b). The time in (b) corresponds to that in Fig. 3. | ||
Discussion
In this paper we studied the motion of a camphor disk in a system with dynamically changing boundaries. There is a coupling between the geometry of the boundaries and the disk motion. The surface concentration of camphor molecules released from the disk generates a torque moving objects reclining on water that define the system boundaries. The geometry of the boundaries affects the surface concentration profile by introducing constraints on the diffusion of camphor molecules. The surface concentration profile determines the camphor disk motion.Our numerical simulations have demonstrated that the interactions between a camphor disk and other objects floating on water can be qualitatively described by the model that links the reaction–diffusion equation for surface camphor concentration with Newton’s equation of motion. We can expect that similar models can be used to simulate other systems in which dynamical coupling between the motion of the camphor disks and the geometry of the boundaries is governed by the surface camphor concentration.
We focused our attention on a gate with swinging wings that allow for unidirectional motion of camphor disks. Experiments have shown that the system illustrated in Fig. 1 works with a high level of reliability. The camphor disk was always transmitted in the expected direction. In most experiments the disk passed through the gate a few seconds after it was placed on the water surface. Neither in experiments nor in simulations have we observed disk propagation in the reverse direction. Therefore, it is natural to consider the gate as a chemo-mechanical signal diode for information coded in the presence or absence of camphor disks on the water surface. This result adds to the other applications of surface phenomena for information processing.27 We have studied gates with different shapes of wings (cf.Fig. 2 and 5 and Movie si1.avi, ESI†) and many of them worked reliably. The gate opens easily if a disk can come to the region in between the wings, so the surface camphor concentration increases and the wings are pushed away. This idea was used to shape the wings from the transmission side of the diode. On the other hand, the wings should close tightly to prevent the increase of camphor concentration between them if a disk approaches the gate from the blocking side. We have also investigated gates with a single wing that can be pushed towards the channel side by a camphor disk. The experiments have shown that such gates were not reliable. Therefore, we think that the construction composed of two wings is the most appropriate for other applications.
The gate forcing unidirectional motion of camphor disks can be incorporated into more complex devices to obtain the required motion of objects. For example, in a ring-shaped water channel a camphor disk can rotate clockwise or anticlockwise.24Fig. 5 illustrates that one can maintain the unidirectional rotation on the ring channel using the gate with swinging wings. The blue plastic sheets shaped the channel and the chamber with the gate. The inner radius of the ring channel was 20 mm, the outer one was 40 mm and thus the width of the ring channel was 20 mm. The chamber where the gate was located was formed by two half-disks with a radius of 20 mm. As seen in Fig. 5a the wings started to open when the disk was circa 40 mm before the opening end. Like in Fig. 2 and 3, the gates remained open until the disk passed through it and closed immediately after the disk passed the wings. In experiments unidirectional rotations of the disk were observed in such systems. A sequence of three consecutive rotations before the disk is trapped between the wings and system boundary is illustrated in Movie, si3.avi, in the ESI.†
The gate can be used to compose networks showing a complex behaviour of camphor particles. It is known3,6–8 that the character of the camphor motion depends on the geometry of the water chamber. Let us assume that a few water chambers forcing different types of motion are connected with channels and gates working as diodes. An example is given in Fig. 6 where a few linear water chambers (marked in blue) are linked by red diodes. The considered chambers split into two channels at one of their ends, as illustrated in Fig. 6. It can be expected that at the junction a camphor disk randomly selects the channel it moves into. If the disk enters the channel with a diode then it passes to another chamber. If it enters the channel without the diode, then after reaching the channel end the disk propagates back towards the other end of the chamber. Assume that we measure the y-coordinate of the disk position and that initially a camphor disk is in chamber 1 of the illustrated system. In the beginning we can expect a few large-amplitude oscillations, followed by some small-amplitude oscillations when the disk stays in chamber 2 and mid-amplitude oscillations when the disk moves to chamber 3. Next large-amplitude oscillations re-appear and the sequence repeats with random transitions between oscillation types mentioned above. We think that designing a system with such complex motion of the camphor disk without the use of diodes would be very difficult.
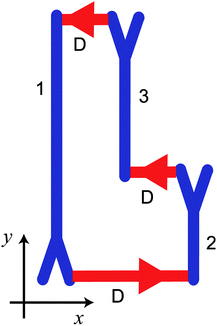 | ||
| Fig. 6 Schematic illustration of a system composed of chambers (1, 2, 3) linked by chemo-mechanical diodes (D) that exhibits a complex time evolution of the y-component of the camphor disk location. | ||
Acknowledgements
We acknowledge Katsuhiko Kayahara and Masakazu Kuze for their assistance with experiments. This work was supported by the JSPS-PAN Bilateral Joint Research Program “Spontaneous creation of chemical computing structures based on interfacial interactions” between Japan and the Polish Academy of Sciences.Notes and references
- C. Tomlinson, Proc. R. Soc. London, 1860, 11, 575 CrossRef.
- L. Rayleigh, Proc. R. Soc. London, 1889, 47, 364 CrossRef.
- S. Nakata, M. Nagayama, H. Kitahata, N. J. Suematsu and T. Hasegawa, Phys. Chem. Chem. Phys., 2015, 17, 10326 RSC.
- S. Soh, K. J. M. Bishop and B. A. Grzybowski, J. Phys. Chem. B, 2008, 112, 10848 CrossRef CAS PubMed.
- N. J. Suematsu, T. Sasaki, S. Nakata and H. Kitahata, Langmuir, 2014, 30, 8101 CrossRef CAS PubMed.
- S. Nakata, S. Y. Hayashima and H. Komoto, Phys. Chem. Chem. Phys., 2000, 2, 2395 RSC.
- Y. Koyano, T. Sakurai and H. Kitahata, Phys. Rev. E, 2016, 94, 042215 CrossRef PubMed.
- S. Nakata, H. Yamamoto, Y. Koyano, O. Yamanaka, Y. Sumino, N. J. Suematsu, H. Kitahata, P. Skrobanska and J. Gorecki, J. Phys. Chem. B, 2016, 120, 9166 CrossRef CAS PubMed.
- S. Nakata, Y. Doi and H. Kitahata, J. Colloid Interface Sci., 2004, 279, 503 CrossRef CAS PubMed.
- S. Nakata, R. Tenno and Y. S. Ikura, Chem. Phys. Lett., 2011, 514, 159 CrossRef CAS.
- Collision-based computing, ed. A. Adamatzky, Springer, 2002 Search PubMed.
- E. Fredkin and T. Toffoli, Int. J. Theor. Phys., 1982, 21, 219 CrossRef.
- K. Yoshikawa, I. N. Motoike, T. Ichino, T. Yamaguchi, Y. Igarashi, J. Gorecki and J. N. Gorecka, Int. J. Unconv. Comput., 2009, 5, 3 Search PubMed.
- J. Gorecka and J. Gorecki, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2003, 67, 067203 CrossRef CAS PubMed.
- J. Gorecki, K. Yoshikawa and Y. Igarashi, J. Phys. Chem. A, 2003, 107, 1664 CrossRef CAS.
- Advances in Unconventional Computing, vol. 1. Theory, vol. 2. Prototypes, Models and Algorithms, ed. A. Adamatzky, Springer, 2017 Search PubMed.
- Á. Tóth, D. Horváth and K. Yoshikawa, Chem. Phys. Lett., 2001, 345, 471 CrossRef.
- K. Agladze, R. R. Aliev, T. Yamaguchi and K. Yoshikawa, J. Phys. Chem., 1996, 100, 13895 CrossRef CAS.
- K. Yoshikawa, T. Kusumi, M. Ukitsu and S. Nakata, Chem. Phys. Lett., 1993, 211, 211 CrossRef CAS.
- É. Pópity-Tóth, V. Pimienta, D. Horváth and A. Tóth, J. Chem. Phys., 2013, 139, 164707 CrossRef PubMed.
- T. Ichino, T. Asahi, H. Kitahata, N. Magome, K. Agladze and K. Yoshikawa, J. Phys. Chem. C, 2008, 112, 3032 CAS.
- Y. S. Ikura, R. Tenno, H. Kitahata, N. J. Suematsu and S. Nakata, J. Phys. Chem. B, 2012, 116, 992 CrossRef CAS PubMed.
- K. Kayahara and M. Kuze, private information.
- M. Nagayama, S. Nakata, Y. Doi and Y. Hayashima, Phys. D, 2004, 194, 151 CrossRef CAS.
- X. Chen, S.-I. Ei and M. Mimura, Networks Heterogeneous Media, 2009, 4, 1 CrossRef.
- H. Kitahata and N. Yoshinaga, arXiv 2016, 1604.01108.
- I. Lagzi, S. Soh, P. J. Wesson, K. P. Browne and B. A. Grzybowski, J. Am. Chem. Soc, 2010, 132, 1198 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: [si1.avi] Experiment with a gate in a straight channel with one and multiple camphor disks (avi). [si2.mpg] Simulations of one camphor disk motion in a gate in a straight channel with Neumann boundary conditions (mpg). [si3.avi] Unidirectional rotation of a camphor disk forced by a diode (avi). See DOI: 10.1039/c7cp03252h |
| This journal is © the Owner Societies 2017 |