How to efficiently tune the biradicaloid nature of acenes by chemical doping with boron and nitrogen

Abstract

Acenes are fascinating polyaromatic compounds that combine impressive semiconductor properties with an open-shell character by varying their molecular sizes. However, the increasing chemical instabilities related to their biradicaloid structures pose a great challenge for synthetic chemistry. Modifying the π-bond topology through chemical doping allows modulation of the electronic properties of graphene-related materials. In spite of the practical importance of these techniques, remarkably little is known about the basic question – the extent of the radical character created or quenched thereby. In this work, we report a high-level computational study on two acene oligomers doubly-doped with boron and nitrogen, respectively. These calculations demonstrate precisely which the chemical route is in order to either quench or enhance the radical character. Moving the dopants from the terminal rings to the central ones leads to a remarkable variation in the biradicaloid character (and thereby also in the chemical stability). This effect is related to a π-charge transfer involving the dopants and the radical carbon centers at the zigzag edges. This study also provides specific guidelines for a rational design of large polyaromatic compounds with enhanced chemical stability.

---

1 Introduction

The n-acenes (C_4n+2H_2n+4) are a class of polyaromatic hydrocarbons (PAHs) composed of linearly condensed benzene rings, resembling a quasi-1D graphene strip with zigzag boundaries. Similar to other π-conjugated systems, the quantum confinement arising from the finite length of acenes determines its basic electronic properties such as band gaps, ionization potential, electron affinity and singlet–triplet (ST) splitting.^1,2 By increasing the carbon framework of oligoacenes, semiconducting properties can already be observed for the medium-sized members pentacene and hexacene, which exhibit high electrical conductivity and low energy gaps that are very attractive for device applications based on organic compounds.^3–5 The trend of vanishing ST splitting with growing acene length indicates the formation of polyradical structures with high chemical instability.^6–9 Thus, the availability of longer acene chains is quite limited and remains a great challenge for experimental research,¹⁰ although recent progress in the synthesis techniques provided oligomers as large as octacene or nonacene under special conditions.¹¹

An efficient strategy for tailoring the electronic, magnetic and physico-chemical properties of graphene-related materials relies on the controlled introduction of substitutional defects (chemical doping).¹² Replacing carbon by boron (B) or nitrogen (N) atoms, for example, allows modulation of the position of frontier energy levels, since these aliovalent species introduce holes or electrons into the π-system via charge transfer. Considerable efforts have been made towards the analysis of the energy gap and transport modulation by doping graphene.^13–16 The dependence of the band structure on graphene doping in various positions¹⁷ and the effect on ionization energies and electron affinities has been studied.^18,19 However, the chemical consequences of heteroatom substitutions in terms of the open-shell nature and stability of these polyaromatic compounds still remain unclear. In particular, the question of how the substitutional B or N doping might be used for tuning the distribution of radical spins in extended acenes is intriguing and opens fascinating opportunities for modulating electronic properties into desired directions. Due to the immanent chemical instability of the n-acenes described above, a reliable documentation of their biradicaloid character is very difficult to obtain from experiments. Quantum chemical calculations, on the other hand, are very well suited to deliver this information and can, thereby, contribute significantly to the efficient development of new organic semiconducting materials.

The present work aims at providing a comprehensive understanding of the structural, electronic and open-shell properties for a series of heteroatom (boron or nitrogen) doped acenes. In our investigation, multireference methods²⁰ will be used which fulfill the challenging needs for a suitable and rigorous treatment of multiradical systems in which the effects of electron unpairing naturally arise from treating the correlated many-body problems. Using the multireference averaged quadratic coupled cluster (MR-AQCC)²¹ method, we investigate how the radical nature of oligoacenes evolves when the dopant position is systematically changed. This information is inferred from simple descriptors such as natural orbital occupation numbers and densities of unpaired electrons,^22–24 which offer a good measure for the singlet open-shell character.^8,25 Moreover, the charge distribution analysis of the π-system provides further insights into the charge transfer process involved in the quenching of the radical character. As an important consequence, the present study provides a comprehensive strategy on how and at which positions to dope the acenes, opening new perspectives for the design of extended PAH compounds with enhanced chemical stability.

2 Methods

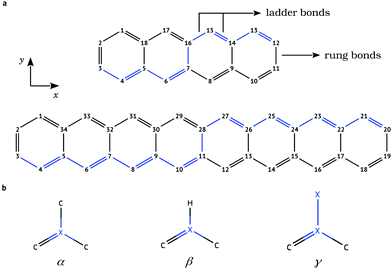
Investigation of chemical doping has been performed for tetracene (C₁₈H₁₂) and octacene (C₃₄H₂₀) by replacing a pair of carbon atoms with an equivalent number of boron (B) or nitrogen (N) heteroatoms (Fig. 1). In both cases, the substitution of two carbon atoms is carried out at symmetric positions with respect to the inversion center of the molecule, starting with the dopants placed at the terminal rings and then changing their positions simultaneously towards the central bond. In this particular substitution scheme, the doped structures belong to the C_2h symmetry point group, where each one of the doping species occupies the (−x,y,0) and (x,−y,0) positions within the carbon backbone. Therefore, 5 and 9 different doping configurations are obtained in the case of tetracene and octacene, respectively, for each N or B doping pair.

Fig. 1 Structures and doping configurations. (a) Schematic molecular structure of pristine tetracene and octacene with the numbering scheme adopted to identify the doping positions. The conjugation path along which doping is carried out is highlighted in blue. (b) Illustration of the three possible substitution patterns of doped oligoacenes according to the local molecular structure around an impurity center, X = B or N: in α-substitution, dopants are coordinated with three C atoms as in a graphene lattice, in β-substitution, two C and one H atoms are covalently bonded to each dopant in a benzene-like form, and γ-substitution corresponds to the case where two dopants are bonded to each other and to two C atoms.

Full geometry relaxations were carried out using the second-order Møller–Plesset perturbation theory²⁶ within the resolution of identity approximation (RI-MP2).²⁷ The triple-ζ valence polarization def2-TZVP basis set²⁸ has been used in all the geometry optimizations.

Electronic correlation effects were taken into account in the framework of multiconfiguration (MC) and multireference (MR) methods. In the former case, complete active space self-consistent field (CASSCF)²⁹ calculations were performed for all structures. The optimized molecular orbitals (MOs) are used in the subsequent MR calculations. Since our focus is the π-conjugated system, the σ orbitals were frozen at the CASSCF level. It has been shown before²⁵ that freezing the σ-system had only a minor influence on unpaired densities and singlet/triplet splittings. Following the experience with a previous study on acenes and periacenes,⁸ the active orbital space comprised eight electrons correlated within eight orbitals, CAS(8,8), of π-symmetry. The selection of the active space was supported by analyzing the deviation threshold of the natural orbital (NO) occupations of the CASSCF calculations from two (occupied) or zero (virtual). For octacene, the actual open-shell structure contains four orbitals (HONO−1, HONO, LUNO, and LUNO+1) with a threshold >0.1 e. Considering an additional threshold of 0.05 e, we found that in total four π occupied orbitals (eight π electrons) and four π unoccupied orbitals, equally chosen from each irreducible representation of the respective symmetry point group, form a good choice for constructing the CAS(8,8) reference space. The same reference space was also used for the smaller tetracene. In the following, the averaged quadratic coupled cluster (MR-AQCC) approach²¹ was applied to expand the correlated many-electron wavefunction in configuration state functions (CSFs) with all single and double excitations from all the reference configurations. In cases where additional CSFs with a significant weight outside of the reference space (intruder states) were detected, all individual CSFs contributing with more than 1% to the AQCC wave function were added to the reference space. The Gaussian polarized 6-31G* basis set was used in all CASSCF and MR-AQCC calculations.

As key quantities for analyzing the radical nature of the doped systems, (i) the natural orbital occupation numbers (NOONs) as computed from the AQCC density by following the deviations of individual NO occupations n_i from zero (unoccupied) and two (doubly occupied), respectively, in conjunction with (ii) the unpaired density and the population of effectively unpaired electrons N_U^22–24 as originally proposed by Takatsuka et al.,^22,23 have been chosen. The nonlinear model of Head-Gordon²⁴ was chosen to evaluate N_U as given by the expression

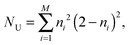where n_i is the occupation of the ith NO and M is the total number of NOs. Accordingly, the open-shell character is maximized when the contribution from each orbital to the effective number of unpaired electrons, N_U, approaches n_i = 1.

The RI-MP2 calculations were performed using the quantum chemical program package ORCA 3.0.3.³⁰ For the MCSCF and MR calculations, we have used the parallel implementation^31,32 of the COLUMBUS program package.^33–36 Post-processing of the MR results was carried out using the TheoDORE program^37,38 to evaluate the Mulliken atomic charges and the partitioning of unpaired densities into atomic contributions.

3 Results and discussion

3.1 Molecular structure

The structures of tetracene and octacene investigated in this work and the definition of bond types are shown in Fig. 1. The MP2 geometry optimization of tetracene accurately reproduces the experimental bond lengths,³⁹ with a largest deviation of −0.04 Å obtained for the C2–C3 and the C11–C12 “rung” bonds (Table S1 in the ESI†). These are continuously elongated when going from the end rings to the central bond. Because of the lack of experimental data for the structures of octacene, the MP2 bond lengths are compared with the values derived from both restricted (RB3LYP) and unrestricted (UB3LYP) DFT geometry optimizations performed by Yang et al.⁴⁰ (see Table S1, ESI†). The C–C bond distances predicted by MP2 are shorter by less than 0.02 Å in comparison with those obtained using RB3LYP. Using the spin-unrestricted formalism for the B3LYP geometries, the difference in the bond length of two successive C–C ladder bonds decreases as well as the length of the rung bonds, bringing the DFT geometries in close accordance with MP2. Also, an even better agreement between MP2 and B3LYP geometries is found for the innermost benzene rings. Another interesting aspect of oligoacenes reproduced by the MP2 calculations is the geometry of the innermost region where successive C–C ladder bonds tend toward equalized lengths, indicating a higher delocalization of the π bonds especially in the octacene.⁴¹ Hence, the electronic properties of the doped acenes should be sensitive not only to the relative separation among the dopants but also to the differences in the local molecular structure.

To evaluate the effects of heteroatomic substitutions on the equilibrium structures of oligoacenes, changes in the bond distances are examined. Due to the different covalent radius of carbons and dopants, all bonds around the B atoms are significantly lengthened, whereas a contraction is observed for N-doping (Tables S2 and S3 in the ESI†). The B–C bond distances vary from 1.48 Å to 1.56 Å, around the typical value of 1.50 Å reported for B-doped graphene nanostructures.^42–44 For N-doping, the N–C rung bonds are the largest ones with the length varying from 1.39 to 1.43 Å, close to DFT values calculated for N–graphene systems.^44–46 These bond length variations around the impurities may induce some strain in the acene backbone, which can be estimated by calculating the deviation of bond lengths from a fully resonant bonding of 1.4 Å (R_i − 1.4), defined here as the resonant bond deviation (RBD). It also provides useful insight into the extent of aromaticity in the sp² carbon network.

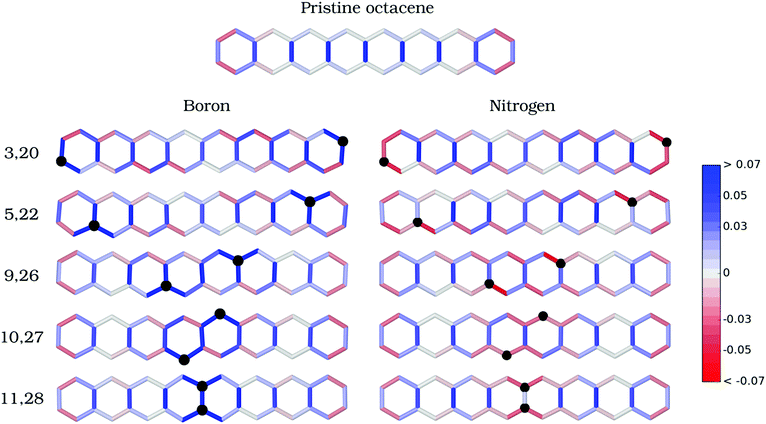
The bond alternation pattern (Fig. 2 and Fig. S1 in the ESI†) for the equilibrium geometry of pristine octacene shows that the rung C–C bond distances are significantly lengthened (0.03 Å) when going from the outermost to the inner benzenoid rings. The adjoining ladder bonds, in turn, assume a fully resonant character with C–C distances of about 1.4 Å, starting already from the second outer rings. This bonding pattern confirms the lower aromaticity of the acene core in long oligomers⁴⁷ and contributes to reducing electronic interaction between the π-systems of the two ladder chains.

Fig. 2 Assessing the doping effects on molecular structures. Alternation of bond lengths (Å) is represented in a color scale according to the deviation from a fully resonant bond length of 1.40 Å for the pristine and doped octacene at five different doping configurations. Bond length contractions are marked in red and stretching are marked in blue. Comparison between the geometries of the pristine molecule and doped systems reveals that the B–C bond lengths are stretched, while the N–C bond lengths are slightly shortened, but in all cases the geometry distortions propagate away from the doping sites.

RBD is strongly affected by introducing B or N defects into the octacene skeleton. The inter-atomic bonds surrounding the B defects have stronger single-bond character upon relaxation (intense blue in Fig. 2), whereas N–C bonds in N2-octacenes (red in Fig. 2) exhibit a markedly higher double-bond character compared to the pristine system. In both cases, the aromaticity of the outermost benzenoid rings in pristine acenes is disrupted by the doping at external positions. Besides the local effects, there is a contraction of the rung bonds away from the B or N dopants. For instance, introducing B impurities at the 3,20-β and 5,22-α positions induces a shortening of the central C11–C28 bond length by 0.02 Å and 0.03 Å with respect to 1.464 Å of the pristine molecule (Fig. S1 in the ESI†). Furthermore, there is a noticeable enhancement in the bond-distance alternation of successive (C–C) ladder bonds for the doped structures compared to pristine octacene (Fig. 2), which is a characteristic of closed-shell quinoidal structures.

3.2 Polyradical character

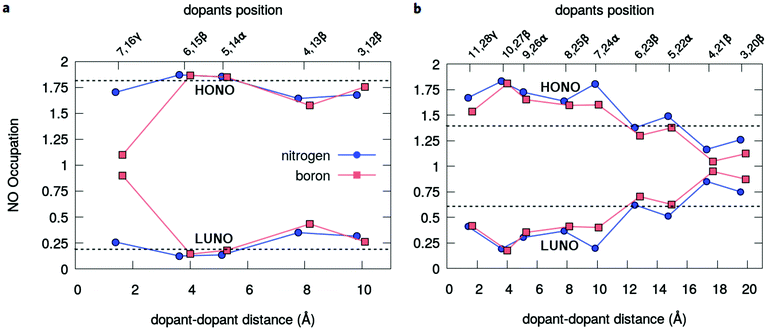
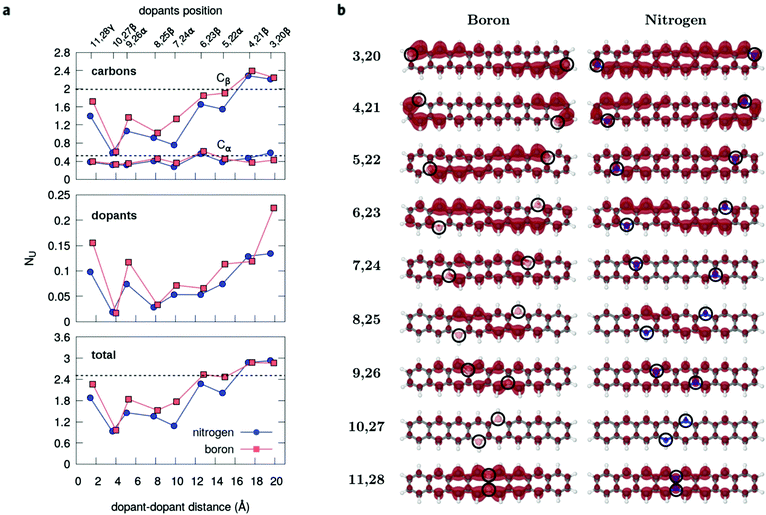
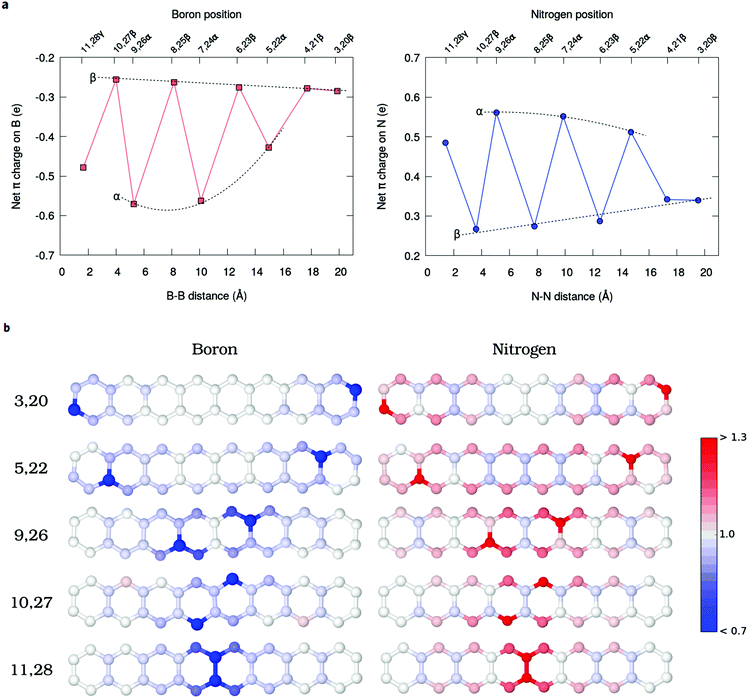
The radical nature of the doped oligoacenes is studied first by evaluating the natural orbital occupation numbers (NOONs) computed from the MR-AQCC density (see the Methods section). Following the highest occupied natural orbital (HONO) and the lowest unoccupied natural orbital (LUNO) along the dual-doped acene series (Fig. 3 and Fig. S2 in the ESI†), there is a general tendency of approaching the HONO/LUNO occupancies towards the closed-shell reference values of two/zero as the doping sites are changed from the outer to the inner rings. Starting with the β-substitution in the outermost rings (which originally have the highest aromaticity, Fig. 2) results in a HONO–LUNO occupation gap of 0.4–0.5 e, indicating a biradical character. This effect is much less pronounced in the doped tetracene case. Especially in the doped octacene series, a gradual quenching in the biradical character is observed, as indicated by a significant increase in the HONO–LUNO occupation gaps, which become larger than those of the pristine molecules (0.8 e for octacene, Fig. 3). The lowest radical character is achieved at the innermost β-configuration (6,15 for tetracene and 10,27 for octacene) with occupation gaps varying around 1.6–1.7 e. Interestingly, N-doping is slightly more effective for reducing the radical character as compared to boron which is noticeably seen in the octacene series (Fig. 3b). For the directly bonded dopants, γ-configuration, there is an increase in the radical character, noticeably higher in the B-doped tetracene. This effect is probably due to the lack of electrons in boron which could induce destabilization of the π-bonding orbitals, mainly in a closed-shell system with a low number of π-electrons.

Fig. 3 Modulation of the radical character. Natural orbital occupation numbers of the frontier levels – the HONO and the LUNO – derived from the correlated MR-AQCC wavefunction for the series of dual-doped (a) tetracene and (b) octacene. The horizontal dashed lines correspond to the reference values calculated for the pristine molecules with the same method.

A comprehensive view on the modulation of the radical character is provided by the analysis of unpaired electrons (Fig. 4). Doping the octacene at the aromatic external rings (3,20β and 4,21β, Fig. 4a), the total number of unpaired electrons, N_U, increases from 2.5 e in pristine octacene to about 3.0 e. The corresponding density is delocalized over the oligomer but has a higher concentration close to the impurities at the terminal rings with a depletion towards the central moiety. This probably reflects the loss of aromatic character due to the doping at the end-rings. As the distance between the dopants decreases towards the center, N_U decreases and achieves its minimal value at the 10,27β configuration with approximately one unpaired electron for both B and N-doping. This tendency is reverted reaching the γ-configuration, but still presenting a lower N_U compared to the pristine acene. These observations are consistent with the analysis based on NO occupation numbers.

Fig. 4 Radical character fingerprints. (a) Evolution of the total number of effectively unpaired electrons (N_U) and its atomic compositions calculated from the MR-AQCC density for the series of dual-doped octacenes, which demonstrate the wide range of the polyradical character achievable. The horizontal dashed line (lower panel) corresponds to the reference value of N_U = 2.5 e obtained for the pristine octacene, of which 2.0 unpaired electrons are distributed over the β-type carbons, C_β, and the remaining 0.5 are located on the α-type, C_α (upper panel). (b) The unpaired electron densities plotted at a 0.002 e Bohr⁻³ isosurface level indicate the spatial regions of a higher polyradical character.

Interestingly, the breakdown of the atomic distribution of N_U (Fig. 4a) reveals that most of the open-shell electrons contributing to the radical behavior of the doped acenes comes from the β-carbons (C_β), whereas the graphene-like carbons C_α contribute with a small amount of 0.2–0.5 unpaired electrons. This is also evidenced by the unpaired density plots (Fig. 4b). The remaining fraction of unpaired electrons is localized on the dopants and follows the same decreasing trend as C_β and the total N_U. Accordingly, C_β and dopants should play a key role in the quenching of the polyradical character. In fact, as shown for pristine n-acenes,^8,48 the distribution of unpaired densities already resides mainly on β-carbons of the zigzag boundaries, which commonly appears to be the rule in many extended PAHs.^8,25,49 Additionally, the population of unpaired electrons in the pristine PAHs^7,48 is increasingly higher around the central moieties of the zigzag edges.

The higher efficiency of N-doping for stabilizing the radical character of acenes is also evidenced by the unpaired electron distribution. Recent experimental studies^50–52 have suggested the introduction of nitrogen atoms into the acene framework (aza-acenes) as one possible route to stabilize longer oligomers. Concomitantly, it has been shown theoretically^53,54 that the hydrogenated forms of aza-acenes with inner N substitutions possess one more aromatic sextet ring compared to their pristine acene counterparts, which explain qualitatively the higher stability of these N-rich compounds according to Clar's rule.^55,56

According to the above discussion based on natural orbital occupations and unpaired electron distributions, our results clearly demonstrate the possibility of tuning the radical character of acenes by means of chemical doping. In particular, the introduction of electrons (holes) into the π-system via N (B) substitutions is more effective in reducing the electron unpairing when doping is performed at the inner β positions. This poses a natural question about the underlying electronic process involved in quenching of the radical character. Further insights into this regard can be obtained from a detailed Mulliken population analysis in conjunction with the distribution of natural orbitals.

3.3 Charge transfer and orbital analysis

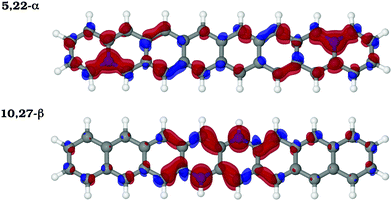
The Mulliken net charges calculated from the MR-AQCC π-density clearly indicate the emergence of a charge transfer process involving the hetero-atomic species B or N (Fig. 5a). Regardless of the doping site, B atoms exhibit a negative net π-charge resulting from the interaction between the empty p-orbital of each B atom and the π-electrons distributed on carbons, which confirms the electron-withdrawing nature of this species with respect to the π-system for doping of graphene nanostructures. Conversely, N atoms donate partially the lone pair electrons for the π-system of octacene as indicated by the positive net-charges (Fig. 5a). Overall, the coordination of the heteroatom with three carbons (α-configurations) presents the highest charge transfer (0.4–0.6 e per dopant) which also increases when going from the end-rings towards the center.

Fig. 5 Charge transfer upon doping. (a) The Mulliken π-charges calculated from the MR-AQCC electron density for the series of dual-doped octacene structures indicate the acceptor and donor characters of B and N impurities, respectively. (b) Color-scale mapping of the Mulliken population of the π electron density illustrating the charge transfer process.

One striking feature of our results is that the extra electron or hole provided by the dopants (as compared to carbon) is partially delocalized in the π-system, but occupying preferably the p_z orbitals of the β-carbons (Fig. 5b). These atoms correspond to those containing the higher amount of unpaired electrons in the pristine molecule. In particular, the central C_βs, which concentrate most of the radical character in acenes, appear as the species most affected by the charge transfer with an increasingly high Mulliken π population for the innermost doping configurations (Fig. 5b). For example, moving the N dopants from the 3,20 to 10,27 β-positions, the π population of C12 and C29 atoms increases from 1.00 e to 1.13 e. To obtain a more detailed view of the charge rearrangements upon chemical doping, the electron density difference (EDD) maps of the π-system (Δρ = ρ_dop − ρ_prist) are illustrated in Fig. 6 for two different N-doped octacene structures chosen as examples. The EDD maps are calculated by subtracting the AQCC π-electron density of the doped structure from that obtained for the pristine one. One can see that there is a large gain of π-electron density mostly around the C_βs atoms upon N-doping. While the EDD isosurfaces also show significant charge rearrangements around some C–C bonds, there is a good correspondence between the charge accumulation regions observed in the EDD isosurfaces and the Mulliken π-population as shown in Fig. 5b, thus confirming the charge transfer process predicted by the Mulliken analysis.

Fig. 6 Rearrangement of the π-electron density upon doping. Isosurface maps of the π-electron density difference (EDD − Δρ = ρ_dop − ρ_prist) calculated for the 5,22-α and 10,27-β N2-octacene structures. The red color indicates charge accumulation regions and the blue color indicates charge depletion.

In the case of the σ-system (Fig. S4 in the ESI†), the net charges are more localized around the dopants and follow a trend related to the difference in electronegativity between the nearest-bonded atoms. Furthermore, the spatial distribution of the HONO and LUNO in doped acenes tends to localize mostly on the C_βs nearest to the impurities, while in the undoped octacene the HONO and LUNO are centralized in the middle of the molecule (Fig. S5 in the ESI†). For the innermost B or N substitutions, there is a notable similar spatial distribution of HONO and LUNO orbitals between the pristine and doped systems. Therefore, for these substitutions, the frontier natural orbitals and the charge transfer involve the same atoms. Taken together, these results suggest that the long-range charge transfer occurring in the π-system upon doping plays an important role in the modulation of the radical character of the acenes.

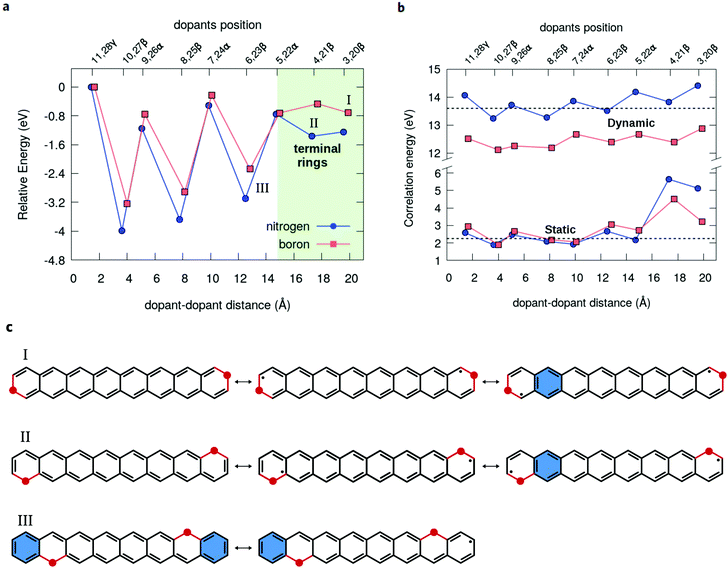
The closed-shell character along the β or α series of dual-doped acenes can be analyzed in terms of energetic stability (Fig. 7a). Upon moving the dopants from the periphery towards the central acene rings, the stabilization is noticeably enhanced for the β-configurations, while there is no clear trend observed for α-configurations. A large energetic stabilization of about 1.6 eV occurs upon changing the dopants in the β-position from the terminal rings to the next ones, probably reflecting an increase in the number of aromatic rings (Fig. 7c). In all cases, the most energetically stable doped structure is found at the 10,27-β substitutional site (Fig. 7a), which also corresponds to the lowest radical structure. As a general aspect, the chemical stabilization of acenes resulting from the doping can be viewed as a competition of two main effects: on the one hand, the quenching of the radical character as the dopants are moved more to the center contributes to the stabilization of the systems but, on the other hand, the increase of electrostatic (Coulomb) repulsion between the dopants leads to an energetic destabilization, which becomes predominant only at the shortest distances. Thus, although the least energetically stable 11,28-γ structures do not have the highest radical character, the shortest separation between the dopants contributes to the destabilization of this structure due to Coulomb repulsion. Overall, nitrogen doping appears to be more effective in stabilizing the oligoacene structures than boron doping, probably due to smaller geometric distortions caused by the impurities.

Fig. 7 Enhancement of the energetic stability upon chemical doping. (a) Relative AQCC energy calculated for the series of boron and nitrogen dual-doped octacene molecules with respect to the total energy of the 11,28 doping configuration. (b) Evolution of the electronic correlation energy calculated as the difference between the MCSCF and HF (static) and MR-AQCC and MCSCF (dynamic) total energies. The horizontal dashed lines represent the reference values obtained for the pristine octacene. (c) Resonance structures of the dual-doped octacene showing an increase in aromaticity as the dopants (in red) are moved from the terminal benzene rings to the next ones along the β positions. Clar's aromatic sextet rings are represented in blue.

Complementary to the above discussion, it is interesting to remark that the progressive decrease in the radical character of the oligoacenes upon chemical doping also reflects in a reduction of the electron-correlation energy (Fig. 7b). The nondynamical (static) contribution for the correlation can be estimated from the differences between the CASSCF and HF total energies, whereas the difference between MR-AQCC and CASSCF gives the dynamic part of the correlation energy. For instance, at the 3,20 pair doping configuration, the static energy is 3.22 eV for B2-octacene and 5.13 eV for N2-octacene, and both numbers decrease up to 1.90 eV for the nearest (non-bonded) dopant separation 10,27.

4 Conclusions

The results presented show that a strong modulation of the radical character of the acenes is attainable through chemical doping by varying the positions of the impurities along the carbon backbone. In particular, inserting the dopants into the outer rings leads to an increase of the radical character compared to the pristine acenes, since these external rings originally possess a higher aromaticity with stronger π-electron bonding and, consequently a smaller unpaired character. As the doping proceeds towards the inner rings, which correspond to the region of higher unpaired electron density of the pristine molecule, the N or B substitutions start to quench the radical character of the acenes. Based on a Mulliken population analysis, this feature was interpreted as the result of a partial charge transfer from the dopants mostly to the β-carbon atoms, which are the centers with the highest electron unpairing in the π-system. In the case of N (B) substitutions, the doubly-occupied (empty) p_z orbital of the impurity atom donates (receives) electrons to (from) the π network, confirming the n-type (p-type) character of the doping. Additionally, the stronger electron pairing of the π-system in doped acenes connected with a lower radical character also results in a relative energetic stabilization of these polyaromatic compounds.

Finally, we should point out that the concise molecular picture derived from our calculations provides a more general understanding about the electronic process underlying the evolution of the radical structure in doped PAHs. In fact, although the present study has focused on a class of quasi-1D polyaromatic systems, they exhibit the feature of localizing the radical spin states in the zigzag boundaries commonly observed in many other extended PAHs, for which the present results can be directly transferred. However, there are other classes of PAHs such as zethrenes or diindeno[b,i]anthracenes^57,58 to name a few, where the analysis of reactive centers is not so clear and where calculations as the ones presented here will provide important support by pinpointing the most chemically reactive centers and tuning their native radical structures through the introduction of donor or acceptor hetero-atomic defects in the carbon skeleton. Thus, the tunability of the diradical character of the acenes demonstrated in the present study through chemical substitutions is a potential route to be explored for designing organic molecules with enhanced nonlinear optical activity^59,60 or with optimized efficiency for singlet fission process in organic photo-voltaic devices^61,62 while retaining the feasibility of chemical synthesis.

Data availability

The data that support the findings of this study are available from the corresponding authors on reasonable request.

Acknowledgements

The financial assistance of the Brazilian agencies Conselho Nacional de Desenvolvimento Científico e Tecnológico (CNPq) and Fundação de Amparo à Pesquisa do Estado de São Paulo (FAPESP) under Projects Process No. 2014/24155-6 and 2015/500118-9 are gratefully acknowledged. The postdoctoral researchers express their gratitude to Coordenação de Aperfeiçoamento de Pessoal de Nível Superior (CAPES) under Project CAPES/ITA 005/2014 by the fellowship. The authors are thankful to the Vienna Scientific Cluster (VSC) under project 70376 for providing the high-performance computational infrastructure and to the FAPESP/Texas Tech University SPRINT program (project no. 2015/50018-9) for travel support.

References

1. M. Y. Han, B. Özyilmaz, Y. Zhang and P. Kim, Phys. Rev. Lett., 2007, 98, 206805.
2. G. D. Scholes and G. Rumbles, Nat. Mater., 2006, 5, 683–696.
3. J. E. Anthony, Angew. Chem., Int. Ed., 2008, 47, 452–483.
4. M. Kitamura and Y. Arakawa, J. Phys.: Condens. Matter, 2008, 20, 184011.
5. M. Watanabe, Y. J. Chang, S.-W. Liu, T.-H. Chao, K. Goto, M. M. Islam, C.-H. Yuan, Y.-T. Tao, T. Shinmyozu and T. J. Chow, Nat. Chem., 2012, 4, 574–578.
6. M. Bendikov, H. M. Duong, K. Starkey, K. N. Houk, E. A. Carter and F. Wudl, J. Am. Chem. Soc., 2004, 126, 7416–7417.
7. J. Hachmann, J. J. Dorando, M. Avilés and G. K.-L. Chan, J. Chem. Phys., 2007, 127, 134309.
8. F. Plasser, H. Pašalić, M. H. Gerzabek, F. Libisch, R. Reiter, J. Burgdörfer, T. Müller, R. Shepard and H. Lischka, Angew. Chem., Int. Ed., 2013, 52, 2581–2584.
9. R. Huang, H. Phan, T. S. Herng, P. Hu, W. Zeng, S.-q. Dong, S. Das, Y. Shen, J. Ding, D. Casanova and J. Wu, J. Am. Chem. Soc., 2016, 138, 10323–10330.
10. R. Einholz, T. Fang, R. Berger, P. Grüninger, A. Früh, T. Chassé, R. F. Fink and H. F. Bettinger, J. Am. Chem. Soc., 2017, 139, 4435–4442.
11. C. Toenshoff and H. F. Bettinger, Angew. Chem., Int. Ed., 2010, 49, 4125–4128.
12. S.-S. Yu and W.-T. Zheng, Nanoscale, 2010, 2, 1069.
13. B. Huang, Q. Yan, G. Zhou, J. Wu, B.-L. Gu, W. Duan and F. Liu, Appl. Phys. Lett., 2007, 91, 253122.
14. J. Gebhardt, R. J. Koch, W. Zhao, O. Höfert, K. Gotterbarm, S. Mammadov, C. Papp, A. Görling, H.-P. Steinrück and T. Seyller, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 155437.
15. N. Ketabi, T. de Boer, M. Karakaya, J. Zhu, R. Podila, A. M. Rao, E. Z. Kurmaev and A. Moewes, RSC Adv., 2016, 6, 56721–56727.
16. P. Nath, S. Chowdhury, D. Sanyal and D. Jana, Carbon, 2014, 73, 275–282.
17. J. Jiang, J. Turnbull, W. Lu, P. Boguslawski and J. Bernholc, J. Chem. Phys., 2012, 136, 014702.
18. A. E. Torres and S. Fomine, Phys. Chem. Chem. Phys., 2015, 17, 10608–10614.
19. A. E. Torres, R. Flores, L. Fomina and S. Fomine, Mol. Simul., 2016, 42, 1512–1518.
20. P. G. Szalay, T. Müller, G. Gidofalvi, H. Lischka and R. Shepard, Chem. Rev., 2012, 112, 108–181.
21. P. G. Szalay and R. J. Bartlett, Chem. Phys. Lett., 1993, 214, 481–488.
22. K. Takatsuka, T. Fueno and K. Yamaguchi, Theor. Chim. Acta, 1978, 48, 175–183.
23. V. N. Staroverov and E. R. Davidson, Chem. Phys. Lett., 2000, 330, 161–168.
24. M. Head-Gordon, Chem. Phys. Lett., 2003, 372, 508–511.
25. A. Das, T. Müller, F. Plasser and H. Lischka, J. Phys. Chem. A, 2016, 120, 1625–1636.
26. C. Møller and M. S. Plesset, Phys. Rev., 1934, 46, 618–622.
27. F. Weigend and M. Häser, Theor. Chem. Acc., 1997, 97, 331–340.
28. F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305.
29. K. Ruedenberg, L. M. Cheung and S. T. Elbert, Int. J. Quantum Chem., 1979, 16, 1069–1101.
30. F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 73–78.
31. H. Dachsel, H. Lischka, R. Shepard, J. Nieplocha and R. J. Harrison, J. Comput. Chem., 1997, 18, 430–448.
32. T. Müller, J. Phys. Chem. A, 2009, 113, 12729–12740.
33. P. G. Szalay, T. Muller and H. Lischka, Phys. Chem. Chem. Phys., 2000, 2, 2067–2073.
34. H. Lischka, R. Shepard, R. M. Pitzer, I. Shavitt, M. Dallos, T. Muller, P. G. Szalay, M. Seth, G. S. Kedziora, S. Yabushita and Z. Zhang, Phys. Chem. Chem. Phys., 2001, 3, 664–673.
35. H. Lischka, T. Müller, P. G. Szalay, I. Shavitt, R. M. Pitzer and R. Shepard, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2011, 1, 191–199.
36. Columbus, an Ab Initio Electronic Structure Program, Release 7.0, 2016, http://https://www.univie.ac.at/columbus/.
37. TheoDORE (Theoretical Density, Orbital Relaxation and Exciton analysis) (1.4), 2016, http://theodore-qc.sourceforge.net.
38. F. Plasser, M. Wormit and A. Dreuw, J. Chem. Phys., 2014, 141, 024106.
39. R. B. Campbell, J. M. Robertson and J. Trotter, Acta Crystallogr., 1962, 15, 289–290.
40. Y. Yang, E. R. Davidson and W. Yang, Proc. Natl. Acad. Sci. U. S. A., 2016, 113, E5098–E5107.
41. D.-e. Jiang and S. Dai, J. Phys. Chem. A, 2008, 112, 332–335.
42. R. H. Miwa, T. B. Martins and A. Fazzio, Nanotechnology, 2008, 19, 155708.
43. R. Faccio, L. Fernández-Werner, H. Pardo, C. Goyenola, O. N. Ventura and A. W. Mombrú, J. Phys. Chem. C, 2010, 114, 18961–18971.
44. N. Al-Aqtash, K. M. Al-Tarawneh, T. Tawalbeh and I. Vasiliev, J. Appl. Phys., 2012, 112, 034304.
45. Y. Fujimoto and S. Saito, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 245446.
46. Z. Wang, J. Xiao and X. Li, Solid State Commun., 2012, 152, 64–67.
47. P. Bultinck, M. Rafat, R. Ponec, B. Van Gheluwe, R. Carbó-Dorca and P. Popelier, J. Phys. Chem. A, 2006, 110, 7642–7648.
48. S. Horn, F. Plasser, T. Müller, F. Libisch, J. Burgdörfer and H. Lischka, Theor. Chem. Acc., 2014, 133, 1511.
49. J. Wang, D. Y. Zubarev, M. R. Philpott, S. Vukovic, W. A. Lester, T. Cui and Y. Kawazoe, Phys. Chem. Chem. Phys., 2010, 12, 9839.
50. B. D. Lindner, J. U. Engelhart, O. Tverskoy, A. L. Appleton, F. Rominger, A. Peters, H.-J. Himmel and U. H. F. Bunz, Angew. Chem., Int. Ed., 2011, 50, 8588–8591.
51. J. U. Engelhart, O. Tverskoy and U. H. F. Bunz, J. Am. Chem. Soc., 2014, 136, 15166–15169.
52. X. Shi and C. Chi, Chem. Rec., 2016, 16, 1690–1700.
53. J. I. Wu, C. S. Wannere, Y. Mo, P. v. R. Schleyer and U. H. F. Bunz, J. Org. Chem., 2009, 74, 4343–4349.
54. R. Rakhi and C. H. Suresh, Phys. Chem. Chem. Phys., 2016, 18, 24631–24641.
55. E. Clar, The aromatic sextet, J. Wiley, 1972.
56. T. Wassmann, A. P. Seitsonen, A. M. Saitta, M. Lazzeri and F. Mauri, J. Am. Chem. Soc., 2010, 132, 3440.
57. Z. Sun, Z. Zeng and J. Wu, Acc. Chem. Res., 2014, 47, 2582–2591.
58. G. E. Rudebusch, J. L. Zafra, K. Jorner, K. Fukuda, J. L. Marshall, I. Arrechea-Marcos, G. L. Espejo, R. Ponce Ortiz, C. J. Gómez-García, L. N. Zakharov, M. Nakano, H. Ottosson, J. Casado and M. M. Haley, Nat. Chem., 2016, 8, 753–759.
59. K. Yoneda, M. Nakano, K. Fukuda and B. Champagne, J. Phys. Chem. Lett., 2012, 3, 3338–3342.
60. S. Muhammad, M. Nakano, A. G. Al-Sehemi, Y. Kitagawa, A. Irfan, A. R. Chaudhry, R. Kishi, S. Ito, K. Yoneda and K. Fukuda, Nanoscale, 2016, 8, 17998–18020.
61. M. B. Smith and J. Michl, Annu. Rev. Phys. Chem., 2013, 64, 361–386.
62. S. Ito and M. Nakano, J. Phys. Chem. C, 2015, 119, 148–157.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c7cp03198j

---