Ultrafast X-ray absorption study of longitudinal–transverse phonon coupling in electrolyte aqueous solution
Abstract
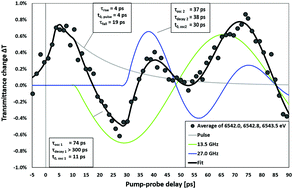
Ultrafast X-ray absorption spectroscopy is applied to study the conversion of longitudinal to transverse phonons in aqueous solution. Permanganate solutes serve as X-ray probe molecules that permit the measurement of the conversion of 13.5 GHz, longitudinal phonons to 27 GHz, transverse phonons that propagate with high-frequency sound speed. The experimental results, combined with QM/MM MD simulations, show that the hydrogen bond network around the charged solutes has a glass-like stiffness that persists for at least tens of picoseconds.
- This article is part of the themed collection: 2017 PCCP HOT Articles


 Please wait while we load your content...
Please wait while we load your content...