B–H⋯π: a nonclassical hydrogen bond or dispersion contact?

Abstract

Close B–H⋯π contacts have recently been observed in crystallographic structures of Ir–dithiolene–phosphine complexes containing boron hydride cluster. This finding was interpreted using quantum chemical calculations as a new type of electrostatically driven nonclassical hydrogen bonding. However, such an explanation contradicts the wealth of evidence for unique noncovalent interactions of boron hydrides. Moreover, care must be exercised when computational methods are used to interpret new phenomena. Therefore, here, we cautiously examine the B–H⋯π interaction by means of advanced quantum chemistry and disprove the claimed attractive electrostatic nature and rather define it as a nonspecific dispersion-driven contact. In summary, we present evidence that the crystallographically observed B–H⋯π contacts do not constitute a novel type of hydrogen bonding of boron hydride clusters.

---

Introduction

Nonclassical (weak) hydrogen bonds are formed between weak donors, such as C–H, and/or weak acceptors, such as π-electron density. They abound in organic compounds and biomolecules (proteins, carbohydrates) and are important contributors to their stability due to their large numbers.¹ As such, they have been widely studied both experimentally and theoretically. By means of quantum chemical (QM) calculations on model systems, it has been ascertained that the electrostatic component of the stabilization energy is reduced as compared to classical hydrogen bonds due to the lowered acidity of the donor and the lowered basicity of the acceptor. Instead, systematically attractive dispersion appears as an important contributor to the stability.²

A “new type of electrostatically attractive B–H⋯π nonclassical hydrogen bonding” has recently been proposed based on crystallographically observed contacts between the boron cluster and phenyl within Ir–dithiolene–phosphine complexes.³ However, the strength of these interactions has very recently been questioned.⁴ Moreover, such an interpretation of the crystallographic data contradicts the wealth of evidence for unique noncovalent interactions of boron hydrides.⁵ The aim of this study is thus to gain deeper insight and to reveal the nature of the noncovalent interactions in the B–H⋯π motif.

Boron hydrides (boranes) are binary inorganic man-made compounds with characteristics vastly differing from organic compounds. Boranes form a large variety of electron-deficient three-dimensional clusters, which are held together by unconventional three-center two-electron (3c2e) B–B–B bonding.⁶ Due to the slightly lower electronegativity of boron than hydrogen, the terminal (exoskeletal) hydrogens of boranes have a hydridic character,⁷ which enables them to form special hydrogen bonds called dihydrogen (or proton–hydride) bonds.^7,8 These are characterized by the interaction between a partially positively charged hydrogen of a proton donor (e.g. CH, NH, OH groups) and an M–H proton acceptor (e.g. a partially negatively charged H atom bound to an electropositive atom M such as B). Any B–H vertex in boranes can be replaced by a heterovertex (yielding heteroboranes, e.g. C–H, carboranes; S thiaboranes), which then acts as an electron donor and is thus a center of a partial positive charge.⁹ This has been proven experimentally by dipole moment measurements in a few cases.¹⁰ In contrast to the terminal (exoskeletal) H atoms, the bridging (μ) H atoms of diborane (B₂H₆) or nido-C₂B₉H₁₃ are bonded through 3c2e bonds and thus bear partial positive atomic charges.⁷ It should be noted here that the concept of atomic partial charges is, on the one hand, useful in assessing electrostatic interactions in molecules but, on the other hand, it is not experimentally observable and thus must be used with caution.⁵ It is known that the widely used natural bond orbital (NBO) method,¹¹ which provides useful insight into the electrostatic properties of organic compounds, does not determine the B–H polarity vector correctly.⁷ The reason for this might be that the NBO method is based on the transformation of the canonical orbitals into the localized ones, which might fail when 3c2e bonding occurs. In contrast, qualitatively correct answers for boron clusters⁷ are obtained when using the restrained fit to the electrostatic potential (RESP) method.¹²

The unique characteristics of heteroboranes give rise to a wide array of their noncovalent interactions.^5,9 Focusing on weak hydrogen bonding, we note two examples here. The first is the C–H⋯π hydrogen bond between the acidic C–H groups of carboranes and the π-electron density of benzene.¹³ The second is the special B₂H⋯π interaction in which the bridging partially positively charged hydrogen of diborane interacts with π systems.¹⁴ In relation to the recent study by Cremer et al.,³ it is however counterintuitive that the terminal boron-bound hydrogens, which should bear a partial negative charge, would form an electrostatically attractive B–H⋯π hydrogen bond with a π-electron density of phenyl. This controversial conclusion may be drawn based on an inappropriate use of NBO for boron clusters as noted above. Alternatively, the polarization of the B–H bond brought about by the close apposition of an H-bond acceptor (phenyl π-electron density) could make the H atom less negative or even neutral, which would enable the H atom to approach the aromatic system more closely, making dispersion stronger. In such a case, carboranes would qualify to the definition of an “amphiphilic noncovalent bonding partner.”¹⁵ Additionally, one could envisage a situation in which the strong electron-withdrawing substituents (such as fluorines or cyano groups) on the phenyl ring create a π-hole (positive region), which would then interact with the B–H hydridic hydrogens.¹⁶ We scrutinize here all these options for the interpretation of B–H⋯π contacts as weak H-bond by means of the advanced QM computational techniques first on the model systems and then on the Ir–dithiolene–phosphine complexes studied by Cremer et al.³

Materials and methods

Model complex preparation

The Ir–dithiolene–phosphine [Cp*Ir-(P(C₆H₅)₃)S₂C₂B₁₀H₁₀] complex designated as B1 in ref. 3 was cut into a carborane⋯benzene complex and the cut bonds were capped by hydrogens. Different orientations were achieved by swapping two B–H and two C–H vertices. The structures were optimized at the density functional theory (DFT) level augmented with empirically parameterized dispersion (DFT-D3) with the default zero-damping function,¹⁷ using the BP86 functional and def2-QZVP basis set in Turbomole 6.6¹⁸ using the Cuby4¹⁹ program. For gradient optimizations, we used the LBFGS algorithm with strict optimization criteria (energy change <0.0006 kcal mol⁻¹, the largest gradient component <0.12 kcal mol⁻¹ Å⁻¹ and the root-mean-square gradient <0.06 kcal mol⁻¹ Å⁻¹). Vibrational frequencies were calculated numerically at the above-mentioned level to confirm that the complexes represent true minima. The trifluoro-toluene (TFT)⋯benzene complex geometry was fully adopted from ref. 15.

Interaction energy calculations

Interaction energies were evaluated at the MP2.5/CBS level²⁰ as the sum of the MP2/CBS energy and the MP2.5 correction. MP2/CBS was approximated by RI-MP2-F12/cc-pVTZ-F12.²¹ The MP2.5 correction term was calculated using the aug-cc-pVDZ basis set. The MP2.5/CBS interaction energies were compared to benchmark CCSD(T)/CBS for the interaction motifs closo-1,2-C₂B₁₀H₁₂⋯benzene complex. CCSD(T)/CBS was computed as the sum of the MP2/CBS energy and the CCSD(T) correction. The CCSD(T)/CBS correction term was determined using the aug-cc-pVTZ basis set. Counterpoise corrections for basis set superposition error (BSSE) were used for all the MP2, MP3, and CCSD(T) energy calculations.

The interaction energy was decomposed using the density functional theory-based symmetry-adapted perturbation theory (DFT-SAPT).²² The inaccurate energies of the virtual orbitals obtained when using the DFT method were corrected by a gradient-controlled shift procedure. The PBE1PBE/aug-cc-pVDZ and PBE1PBE/TZVP calculations were carried out to obtain the desired shift value. The DFT part was treated using the localized and asymptotically corrected LPBE0AC exchange–correlation functional with density fitting and the aug-cc-pVDZ basis set. This combination of the functional and the basis set has been shown to provide a reasonably good description of electrostatic and induction energies, but the dispersion term is underestimated by approximately 10–20%.²³ We used the specific scaling factor optimized for heteroborane cages (the factor of 1.148) to scale the dispersion energy to obtain results comparable with the CBS data.^9b

Spin states of crystallographic B1 complex

The energetic stabilities of states of different multiplicity (low-spin singlet and triplet and high-spin quintet) were calculated on the crystallographic geometry of the B1 complex³ using unrestricted DFT-D3 at the BP86/def2-QZVP level (def2-ecp for Ir) in Turbomole 6.6.¹⁸

Electrostatic potentials

ESPs were computed at the HF/cc-pVDZ level (the CEP-121G basis set and pseudopotential were used for the Ir atom). It has recently been shown that this basis set size is sufficient for these purposes.²⁴ Differential electron densities (DED) defined as the difference between the complex electron density and the sum of the monomer electron densities as well as ESPs along the main intermolecular coordinate were calculated at the HF/cc-pVTZ level, all using Gaussian09²⁵ and Molekel4.3²⁶ programs. Dipole moments were calculated at the HF/cc-pVDZ level of theory.

Results and discussion

Electrostatic properties of isolated molecules

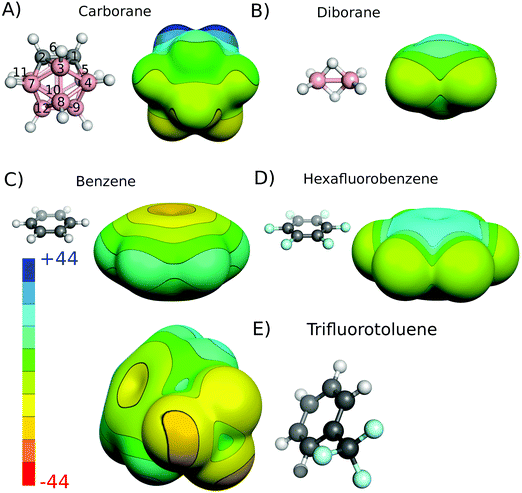
The charge distribution of molecules that underlie their noncovalent interactions can be inferred from their experimental or quantum mechanically (QM) calculated electrostatic potentials (ESPs). For the closo-1,2-C₂B₁₀H₁₂ neutral carborane, the calculated carbon-bound hydrogens have a highly positive ESP surface (Fig. 1A). The magnitude of the ESP surface on the top of the vertex (V_s) is about 40 kcal mol⁻¹ (Table 1). Antipodally to the C–H vertices, the B–H(9) and B–H(12) vertices have a highly negative ESP surface with a minimum of −9.4 kcal mol⁻¹ (Fig. 1A and Table 1). Indeed, the middle point of the CC vector is the center of partially positive charge, which has also been determined experimentally in an unambiguous way by interpreting the dipole moment in terms of a simple vector algebra.^10a It should be stressed that the closo-1,2-C₂B₁₀H₁₂ molecules exhibit a very large dipole moment of 4.5 D, measured experimentally.^10a A comparably large dipole moment of 4.5 D can be found in benzonitrile (C₆H₅CN) for example.²⁷ Consistent with the previous findings,^7a,14 the bridging (μ) hydrogen atoms of diborane have a positive ESP surface while the terminal hydrogen atoms of diborane have a negative ESP surface (Fig. 1B).

Fig. 1 Molecular structures and computed electrostatic potential (ESP) of closo-1,2-C₂B₁₀H₁₂, diborane, benzene, hexafluorobenzene, and trifluorotoluene. The standard vertex numbering of closo-1,2-C₂B₁₀H₁₂ is shown. The ESP has been computed on the 0.001 a.u. molecular surface at the HF/cc-pVDZ level. The ESP color range in kcal mol⁻¹. The atom color coding is as follows: pink – B; gray – C; cyan – F; white – H.

Table 1 Magnitude (V_s) of the computed electrostatic potential surface (ESP) of closo-1,2-C₂B₁₀H₁₂ computed on the 0.001 a.u. molecular surface at the HF/cc-pVDZ level. Atom numbering as in Fig. 1A. All energies are in kcal mol⁻¹

Vertex	V s on the top of the H atom
CH (1, 2)	40.2
BH (3, 6)	10.0
BH (4, 5, 7, 11)	1.9
BH (8, 10)	−6.3
BH (9, 12)	−9.4

---

An alternative view on the electrostatic properties of molecules is given by QM computed partial atomic charges. This concept, however, does not correspond to an experimental observable and must thus be used with caution. It has been shown for anionic heteroboranes⁷ that the NBO method gives partial charges inconsistent with their experimentally observed capability of dihydrogen bonding.⁸ In contrast, the RESP method provides correct partial negative charges on boron-bound hydrogens.⁷ In Table 2, these findings are extended to the neutral closo-1,2-C₂B₁₀H₁₂.

Table 2 Partial atomic charges (in e⁻) of isolated closo-1,2-C₂B₁₀H₁₂ computed by different QM methods at the DFT level (B3LYP functional). Atom numbering is shown in Fig. 1A

	RESP		NBO
	cc-pVDZ		cc-pVTZ	cc-pVQZ
	UFF radii	MK radii
C (1, 2)	−0.03	−0.01	−0.37	−0.41
B (3, 6)	−0.01	0.01	0.08	0.09
B (4, 5, 7, 11)	0.00	0.03	−0.05	−0.03
B (8, 10)	0.02	0.06	−0.17	−0.17
B (9, 12)	0.00	0.03	−0.15	−0.14
H (1, 2)	0.17	0.15	0.29	0.31
H (3, 6)	−0.02	−0.04	0.07	0.07
H (4, 5, 7, 11)	−0.03	−0.05	0.08	0.08
H (8, 10)	−0.04	−0.07	0.09	0.08
H (9, 12)	−0.04	−0.07	0.08	0.08

---

Model complexes

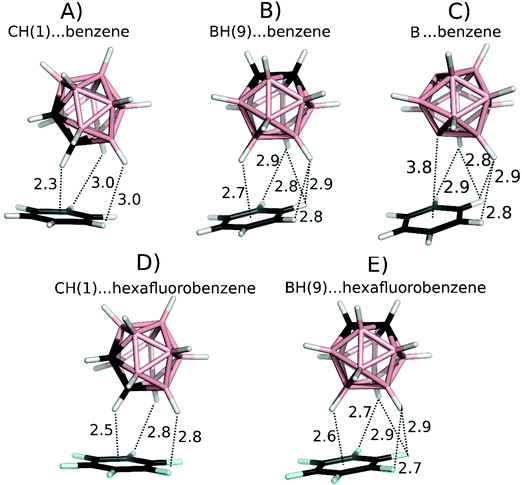
The DFT-D3 optimized geometries of the model complexes featuring C–H⋯π, B–H⋯π, C–H⋯π-hole, and B–H⋯π-hole interactions (Fig. 2) served for the calculations of interaction energies using the highly accurate MP2.5/CBS and benchmark CCSD(T)/CBS methods.²⁰

Fig. 2 Optimized structures of the complexes of closo-1,2-C₂B₁₀H₁₂ and closo-1,7-dehydro-B₁₂H₁₀ with benzene and hexafluorobenzene. The distances are in Å. The element color coding is as follows: pink – B; black – C; cyan – F; white – H.

The MP2.5 results were in good agreement with the CCSD(T) benchmark data – with a root-mean-square error (RMSE) of 0.22 kcal mol⁻¹ (Table 3). The novel “B–H⋯π H-bond” (Fig. 2B)³ can be compared to the known C–H⋯π weak H-bond of carboranes (Fig. 2A).^13,14a Geometrically, the C–H⋯π motif was about 0.6 Å shorter than the B–H⋯π in the studied closo-1,2-C₂B₁₀H₁₂⋯benzene complex. Energetically, the computed interaction energies showed that the B–H⋯π interaction (maximal interaction of −3.50 kcal mol⁻¹) was about half the strength of the C–H⋯π interaction (−6.35 kcal mol⁻¹; Table 3). It should also be noted that the DFT-D3 method overestimated both types of these interactions by about 1 kcal mol⁻¹, thus seemingly increasing the relative strength of the B–H⋯π versus the C–H⋯π interaction.

Table 3 Interaction energies and their components (all in kcal mol⁻¹) of closo-1,2-C₂B₁₀H₁₂⋯benzene, closo-1,7-dehydro-B₁₂H₁₀⋯benzene and closo-1,2-C₂B₁₀H₁₂⋯hexafluorobenzene complexes^a

Interaction motif	MP2.5/CCSD(T)	DFT-D3/BP-86/def2-QZVP	DFT-SAPT total
	ΔE	ΔE	E ^pol1	E ^exch1	E ^ind	E ^disp2	ΔE
a The interaction energy (ΔE) and its decomposition into electrostatic (E^pol1), exchange–repulsion (E^exc1), dispersion (E^disp2) and induction (E^ind) terms; energy in kcal mol^−1. b E ^ind = E^ind2 + E^ex-ind2 + δHF.
closo-1,2-C2B10H12⋯benzene
C–H(1)⋯C6H6	−6.58/−6.35	−7.18	−5.02	9.22	−1.82	−8.84	−6.46
B–H(9)⋯C6H6	−2.65/−2.58	−3.48	−1.94	7.21	−0.64	−7.50	−2.86
B–H(8)⋯C6H6	−2.79/−2.71	−3.61	−2.07	7.30	−0.66	−7.53	−2.95
B–H(3)⋯C6H6	−3.10/−3.50	−4.41	−3.17	8.32	−0.87	−7.96	−3.68
B–H(4)⋯C6H6	−3.21/−3.11	−4.01	−2.60	7.72	−0.76	−7.90	−3.54
closo-1,7-Dehydro-B12H10⋯benzene
B⋯C6H6	−4.18	−4.42	−2.99	5.10	−0.69	−5.83	−4.14
closo-1,2-C2B10H12⋯hexafluorobenzene
C–H(1)⋯C6F6	−3.30	−4.86	−1.63	8.81	−1.27	−9.38	−3.47
B–H(9)⋯C6F6	−4.89	−5.72	−4.19	9.46	−0.78	−9.44	−4.95
B–H(8)⋯C6F6	−4.75	−5.63	−4.19	9.63	−0.81	−9.50	−4.87
B–H(3)⋯C6F6	−4.03	−5.07	−3.11	8.70	−0.78	−9.00	−4.20
B–H(4)⋯C6F6	−4.36	−5.31	−3.49	8.89	−0.77	−9.12	−4.48

---

To understand the driving forces behind the noncovalent interactions in the studied complexes, we applied a computational partitioning of the interaction energy terms. Among various techniques allowing energy partitioning, the DFT-SAPT²² method provides the most reliable results; the polarization/electrostatic, exchange–repulsion, induction, and dispersion energy terms for the benzene⋯carborane complexes are presented in Table 3. It is evident that the C–H⋯π motif has a large dispersion component (−8.84 kcal mol⁻¹), followed by electrostatics (−5.02 kcal mol⁻¹) and induction (−1.82 kcal mol⁻¹) in accordance with previous calculations.^2b,14a All the B–H⋯π motifs have a similarly large dispersion component (−7.50 to −8.00 kcal mol⁻¹) and, in contrast to the CH⋯π motif, the electrostatic and induction terms are weaker (−1.94 to −3.17 kcal mol⁻¹ for electrostatics and −0.64 to −0.87 for induction). However, the electrostatic term is not repulsive, as could be expected from simple electrostatic considerations. This might be due to the fact that the repulsive B–H⋯π interaction is accompanied by four attractive C–H⋯H–B dihydrogen bonds with H⋯H distances of about 2.8 Å (see Fig. 2B). To test this hypothesis, we replaced the B–H vertex with a bare B vertex in closo-1,7-dehydro-B₁₂H₁₀²⁸ keeping the binding motif unchanged (see Fig. 2C). Upon the elimination of the B–H⋯π contact, the electrostatic term became more favorable by about 1 kcal mol⁻¹ (from −1.94 to −2.99 kcal mol⁻¹), which clearly indicates that the B–H⋯π contact was electrostatically repulsive. The interaction between the B and π-electrons is negligible due to the large distance of 3.8 Å.

The charge-transfer energy is not a separated energy component in the DFT-SAPT analyses and it is included in the induction term. We opted for the constrained DFT calculation of the charge-transfer energy, which yields reliable and robust results with respect to the strength of the charge transfer, the basis set size, and the DFT functional used.²⁹ The computed charge-transfer energy is small for all the carborane⋯benzene complexes (ranging between 0 and −0.10 kcal mol⁻¹). This is in agreement with the finding that the induction term was much less attractive than dispersion or electrostatic terms in the DFT-SAPT analysis.

Although the induction term was considerably smaller than the dispersion and electrostatic terms in the DFT-SAPT analysis, it should not be underestimated. In order to test whether the closo-1,2-C₂B₁₀H₁₂ molecule may be an “amphiphilic nonbonding partner”, as has recently been shown for trifluorotoluene (TFT),¹⁵ we compared the polarization of the B(9)–H bond in the closo-1,2-C₂B₁₀H₁₂⋯benzene complex in B(9)–H geometry (Fig. 2B) with the polarization of the CF₃ group in the trifluoro-toluene (TFT)⋯benzene complex, whose geometry was adopted from ref. 15. We first analyzed the shift in the electron density of the studied molecules upon the complex formation, i.e. the isodensity of the differential electron density (DED) shown in Fig. 3.

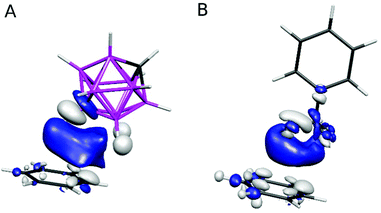Fig. 3 Differential electron densities (DED) of the closo-1,2-C₂B₁₀H₁₂⋯benzene complex in B(9)–H geometry (A) and the trifluorotoluene⋯benzene complex (B). The ±0.00033 a.u. isodensity is depicted. Atom color coding as in Fig. 2; DED color coding: white – positive isodensity surface, blue – negative isodensity surface.

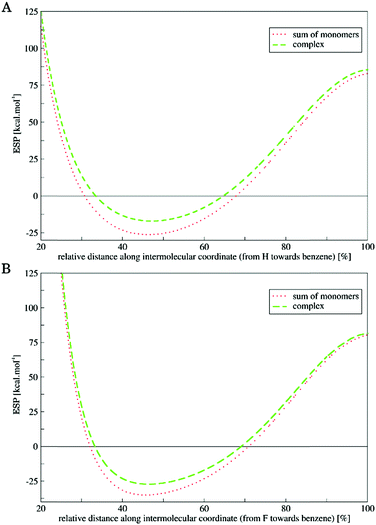
The DED of both the complexes exhibited regions with positive values (increased electron density) located at the monomers (white clouds, cf.Fig. 3) and regions with negative values (decreased electron density) in the inter-monomer areas (blue clouds, cf.Fig. 3). This indicates that upon interaction the electron density was shifted from the regions in between the monomers to the region located at the particular monomers. Second, we compared the ESPs of the complexes with those of the sum of the ESPs of the monomers (see Fig. 4).

Fig. 4 ESPs of the closo-1,2-C₂B₁₀H₁₂⋯benzene complex in B(9)–H geometry (A) and the trifluorotoluene⋯benzene complex (B). ESPs are calculated along the main intermolecular coordinate, i.e. along the B–H⋯π and C–F⋯π noncovalent bonds (from H/F toward the benzene; π ring is represented with the center of mass of the carbon ring); ESP line coding: dashed – complex, dotted – sum of the monomers.

The ESP in the region about the van der Waals radius of both the H^δ− and F^δ− became less negative when the interaction was present (complex vs. sum of the monomers) in both cases. This change of the ESP proves that the electron density was shifted from the regions in-between monomers upon interaction. This is in full agreement with the DED maps described above (cf.Fig. 3). The polarized electron density makes the size of H^δ−/F^δ− effectively smaller, which allows monomers to approach each other more closely. Consequently, it allows the dispersion component to be stronger. Hence, we can conclude that the BH^δ− vector of closo-1,2-C₂B₁₀H₁₂ carborane represents another type of amphiphilic moiety, besides the CF₃^δ− group of TFT. However, in the latter case, it is more pronounced due to the anomeric effect (negative hyperconjugation),³⁰ smaller dipole moment (2.7 vs. 4.5 D for TFT and closo-1,2-C₂B₁₀H₁₂, respectively), and a partial positive charge on the C atom of the CF₃ group (see also ESP in Fig. 1). Let us note that the amphiphilicity of the BH groups of carborane will be influenced by their position on the cage, i.e. growing in the order BH (9, 12) < BH (8, 10) < BH(4, 5, 7, 11) < BH (3, 6).

To understand the characteristics of a potential B–H⋯π-hole interaction, we replaced benzene in the CH(1) and BH(9) model complexes (Fig. 2A and B) with hexafluorobenzene. While benzene acts as an electron donor, hexafluorobenzene acts as an electron acceptor.¹⁶Fig. 1C and D shows the ESP of both the systems, with the π-hole of the latter clearly visible. Interaction energies and the DFT-SAPT energy components are shown in Table 3. These results clearly show the differences between the C–H and B–H interactions with π-electrons and a π-hole. B–H⋯π-hole complexes are analogous to C–H⋯π complexes. Both are characterized by a large interaction energy (−4.0 to −4.9 and −6.4 kcal mol⁻¹ for B–H⋯π-hole and C–H⋯π, respectively) and an important electrostatic energy component (−3.1 to −4.2 and −5.0 kcal mol⁻¹ for B–H⋯π-hole and C–H⋯π, respectively). On the other hand, B–H⋯π complexes are analogous to C–H⋯π-hole complexes. Both are characterized by a small interaction energy (−2.6 to −3.5 and −3.3 kcal mol⁻¹ for B–H⋯π and C–H⋯π-hole, respectively) and a small electrostatic energy component (−1.9 to −3.2 and −1.6 kcal mol⁻¹ for B–H⋯π and C–H⋯π-hole, respectively). It can thus be concluded that the B–H⋯π contacts observed in the crystallographic complexes³ do not represent a novel H-bonding interaction but rather a nonspecific dispersion-driven contact.

Ir–dithiolene–phosphine complexes

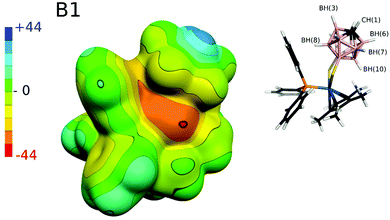
Having found the nonspecific weak dispersion-driven nature of B–H⋯π interactions in model carborane⋯benzene complexes, we wanted to understand the characteristics of this structural motif in the Ir–dithiolene–phosphine [Cp*Ir-(P(C₆H₅)₃)S₂C₂B₁₀H₁₀] complex designated as B1 in ref. 3. To this aim, we first tested the stability of different spin states of Ir in the complex. We found that the low-spin singlet was by 51.5 and 110.0 kcal mol⁻¹, respectively, more stable than the low-spin triplet and high-spin quintet and, therefore, the former spin state was used for the ESP calculation (Fig. 5).

Fig. 5 Computed electrostatic potential (ESP) of the Ir–dithiolene–phosphine [Cp*Ir-(P(C₆H₅)₃)S₂C₂B₁₀H₁₀] complex (B1) on a 0.001 a.u. molecular surface computed at the UHF/cc-pVDZ level (for Ir, the CEP-121G basis set was used). The ESP color range is in kcal mol⁻¹. The atom color coding is as follows: pink – B; black – C; white – H, yellow – S, blue – Ir, orange – P.

In line with our findings on the isolated carborane above (Tables 1 and 2), the BH(8) group in contact with the phenyl moiety bears a hydridic hydrogen (Table 4) and furthermore, no π-hole can be found on the benzene ring approaching the B–H vertex (Fig. 5). In agreement with the above-mentioned discussion on the model complexes, the calculated ESP surface of the B1 system (Fig. 5) confirms that there is no specific electrostatically driven attractive interaction between the B–H and phenyl groups in the B1 system and rather the B–H⋯π contact is dispersion driven.

Table 4 Partial atomic charges and magnitude (V_s) of the electrostatic potential surface (ESP) of selected hydrogen atoms in the B1 molecule computed at the HF/cc-pVDZ level (for Ir the CEP-121G basis set was used). Charges and V_s are in e⁻ and kcal mol⁻¹, respectively

Vertex	V s on the top of the H atom	RESP partial atomic charge on the H atom
C–H (1, 2)	31.4	0.16
B–H (3, 6)	2.5	−0.02
B–H (4, 5, 7, 11)	−7.5	−0.03
B–H (8, 10)	Not accessible	−0.01

---

Conclusions

The nature of interaction in the B–H⋯π motif observed crystallographically in Ir–dithiolene–phosphine complexes³ has been studied here by means of advanced QM calculations including energy decomposition to physical terms. We have shown that the B–H⋯π motif is not an electrostatically attractive nonclassical hydrogen bond but rather a nonspecific weak dispersion-driven B–H⋯π contact.

Acknowledgements

This work was supported by the research project RVO 61388963 of the Czech Academy of Sciences. We acknowledge the financial support of the Czech Science Foundation (AP, JR, RS, ML, PH: P208/12/G016 and JF, DH: 17-08045S). This work was supported by the Ministry of Education, Youth and Sports from the Large Infrastructures for Research, Experimental Development and Innovations project “IT4Innovations National Supercomputing Center – LM2015070” as well as from the project LO1305 (PH).

Notes and references

1. (a) G. R. Desiraju and T. Steiner, The Weak Hydrogen Bond, Oxford University Press, Oxford, 1999; (b) S. Tsuzuki, T. Uchimaru and M. Mikami, J. Phys. Chem. B, 2009, 113, 5617; (c) M. Brandl, M. S. Weiss, A. Jabs, J. Suhnel and R. Hilgenfeld, J. Mol. Biol., 2001, 307, 357.
2. (a) W. Zierkiewicz, P. Jurečka and P. Hobza, ChemPhysChem, 2005, 6, 609; (b) S. Tsuzuki and A. Fujii, Phys. Chem. Chem. Phys., 2008, 10, 2584.
3. X. Zhang, H. Dai, H. Yan, W. Zou and D. Cremer, J. Am. Chem. Soc., 2016, 138, 4334.
4. J. Grunenberg, Chem. – Eur. J., 2016, 22, 18678.
5. R. Sedlak, J. Fanfrlík, A. Pecina, D. Hnyk, P. Hobza and M. Lepšík, Boron – the Fifth Element, Challenges and Advances in Computational Chemistry and Physics, ed. D. Hnyk and M. McKee, Springer, Heidelberg, New York, Dordrecht and London, 2015, ch. 9, vol. 20.
6. W. N. Lipscomb, In Boron Hydrides, W. A. Benjamin, Inc., New York, 1963.
7. (a) J. Fanfrlík, M. Lepšík, D. Hořínek, Z. Havlas and P. Hobza, ChemPhysChem, 2006, 7, 1100; (b) J. Fanfrlík, D. Hnyk and M. Lepšík, and P. Hobza, Phys. Chem. Chem. Phys., 2007, 9, 2085.
8. (a) N. V. Belkova, E. S. Shubina and L. M. Epstein, Acc. Chem. Res., 2005, 38, 624; (b) R. Custelcean and J. E. Jackson, Chem. Rev., 2001, 101, 1963.
9. (a) J. Fanfrlík, A. Přáda, Z. Padělková, A. Pecina, J. Macháček, M. Lepšík, J. Holub, A. Růžička, D. Hnyk and P. Hobza, Angew. Chem., Int. Ed., 2014, 53, 10139; (b) A. Pecina, M. Lepšík, D. Hnyk, P. Hobza and J. Fanfrlík, J. Phys. Chem. A, 2015, 119, 1388; (c) J. Fanfrlik and D. Hnyk, CrystEngComm, 2016, 18, 8982.
10. (a) D. Hnyk, V. Všetečka, L. Drož and O. Exner, Collect. Czech. Chem. Commun., 2001, 66, 1375; (b) J. Machacek, J. Plesek, J. Holub, D. Hnyk, V. Vsetecka, I. Cisarova, M. Kaupp and B. Stibr, Dalton Trans., 2006, 1024.
11. A. E. Reed, L. A. Curtiss and F. Weinhold, Chem. Rev., 1988, 88, 899.
12. C. I. Bayly, P. Cieplak, W. D. Cornell and P. A. Kollman, J. Phys. Chem., 1993, 97, 10269.
13. (a) R. J. Blanch, M. Williams, G. D. Fallon, M. G. Gardiner, R. Kaddour and C. L. Raston, Angew. Chem., Int. Ed., 1997, 36, 504; (b) C. L. Raston and G. W. V. Cave, Chem. – Eur. J., 2004, 10, 279.
14. (a) R. Sedlák, J. Fanfrlík, D. Hnyk, P. Hobza and M. Lepšík, J. Phys. Chem. A, 2010, 114, 11304; (b) S. X. Tian, H.-B. Li, Y. Bai and J. Yang, J. Phys. Chem. A, 2008, 112, 8121; (c) H. Li, D. Min, S. G. Shore, W. N. Lipscomb and W. Yang, Inorg. Chem., 2007, 46, 3956; (d) P. K. Bhattacharyya, New J. Chem., 2017, 41, 1293.
15. C. Esterhuysen, A. Hesselmann and T. Clark, ChemPhysChem, 2017, 18, 1.
16. H. Wang, W. Wang and W. Jin, J. Chem. Rev., 2016, 116, 5072.
17. S. Grimme, J. Antony, S. Ehrlich and H. A. Krieg, J. Chem. Phys., 2010, 132, 154104.
18. R. Ahlrichs, M. Bär, M. Häser, H. Hom and C. Kölmel, Chem. Phys. Lett., 1989, 162, 165.
19. J. Řezáč, J. Comput. Chem., 2016, 37, 1230.
20. (a) M. Pitonák, P. Neogrády, J. Cerný, S. Grimme and P. Hobza, ChemPhysChem, 2009, 10, 282; (b) J. Řezáč and P. Hobza, Chem. Rev., 2016, 116, 5038.
21. K. A. Peterson, T. B. Adler and H.-J. Werner, J. Chem. Phys., 2008, 128, 084102.
22. (a) B. Jeziorski, R. Moszynski and K. Szalewicz, Chem. Rev., 1994, 94, 1887; (b) H. L. Williams and C. F. Chabalowski, J. Phys. Chem. A, 2001, 105, 646; (c) G. Jansen and A. Hesselmann, Chem. Phys. Lett., 2002, 357, 464; (d) J. Misquitta and K. Szalewicz, Chem. Phys. Lett., 2002, 357, 301; (e) J. Misquitta, R. Podeszwa, B. Jeziorski and K. Szalewicz, J. Chem. Phys., 2005, 123, 214103.
23. A. Hesselman, G. Jansen and M. Schütz, J. Chem. Phys., 2005, 122, 14103.
24. K. E. Riley, K.-A. Tran, P. Lane, J. S. Murray and P. Politzer, J. Comput. Sci., 2016, 17, 273.
25. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, T. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 09, Revision A.02, Gaussian, Inc., Wallingford CT, 2016.
26. P. Flukiger, H. P. Luthi, S. Sortmann and J. Weber, Molekel 4.3, 2000–2002.
27. K. Wohlfart, M. Schnell, J.-U. Grabow and J. Kupper, J. Mol. Spectrosc., 2008, 247, 119.
28. P. D. Pancharatna, M. M. Balakrishnarajan, E. D. Jemmis and R. Hoffman, J. Am. Chem. Soc., 2012, 134, 5916 . Additionally, 3 naked boron vertices are known in closo,closo-[B₂₁H₁₈]⁻ reported in; E. Bernhardt, D. J. Brauer, M. Finze and H. Willner, Angew. Chem., 2007, 46, 2927 , and 4 naked boron vertices in closo,closo-[B₂₀H₁₆] reported in; D. Hnyk, J. Holub, T. Jelínek, J. Macháček and M. G. S. Londesborough, Collect. Czech. Chem. Commun., 2010, 75, 1115 and the references therein. Similarly, naked C vertices in heteroboranes were observed in closo-1,2-dehydro-1,2-C₂B₁₀H₁₀ reported in; Z. Qiu and Z. Xie, Dalton Trans., 2014, 43, 4925.
29. J. Řezáč and A. de la Lande, J. Chem. Theory Comput., 2015, 11, 528.
30. A. E. Reed and P. von Ragué Schleyer, J. Am. Chem. Soc., 1987, 109, 7362.

---

Footnote

† We dedicate this study to our colleague and friend Prof. Dieter Cremer who passed away in April, 2017.

---