Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
On the role of topology in regulating transcriptional cascades†
Mahan
Ghafari
ab and
Alireza
Mashaghi
 *a
*a
aLeiden Academic Centre for Drug Research, Faculty of Mathematics and Natural Sciences, Leiden University, Leiden, The Netherlands. E-mail: a.mashaghi.tabari@lacdr.leidenuniv.nl
bDepartment of Physics, Emory University, Atlanta, GA 30322, USA
First published on 8th September 2017
Abstract
We study the impact of topology on the response of a transcriptional cascade with certain circuit topologies to a constant and time-varying input signal. We systematically analyze the response of the output to activating and repressing cascades. We identify two types of responses for a linear cascade, namely the “Decaying mode”, where the input signal becomes exceedingly weaker as it propagates, and the “Bistable mode”, where the input signal can either be amplified or die out in the pathway. We examine how the transition occurs from one mode to the other as we add coherent and/or incoherent feed-forward loops in an otherwise linear cascade. We find that pathways with at least one incoherent feedforward loop can perform adaptive responses with the quality of response varying among different topologies. Furthermore, we study the origin of a (non)monotonic input–output profile for various circuit topologies over a wide range of parameter space. For a time-varying input signal, we identify some circuit topologies that are more prone to noise propagation than others that are more reliable in blocking out high-amplitude fluctuations. We discuss the effect of cell to cell variation in protein expression on the output of a linear cascade and compare the robustness of activating and repressing cascades to noise propagations. In the end, we apply our model to study an example of a transcription cascade that guides the development of Bacillus subtilis spores and discuss an example from a metabolic pathway where a transition from the decaying to bistable mode can occur by changing the topology of interactions in the pathway.
1 Introduction
Genome-wide studies of transcriptional networks have demonstrated a huge complexity of interactions among many components of gene expression networks, often referred to as “hairball” diagrams. This level of complexity makes it difficult to formulate unifying approaches towards understanding the dynamics of such networks and arrive at useful conclusions.1 Topology plays a critical role in determining the relation between various parts of the network and how they function together. To understand the role of topology in governing the dynamics of transcriptional regulatory networks such as sensory networks that respond to signals such as stresses and nutrients, and developmental networks that govern differentiation process, many approaches have been developed to estimate the expression levels of interacting elements, how interactions change with time in response to environmental cues, and the impact of topology on the robustness of the responses.2–5 In recent years, various topological features of signaling pathways have been identified and their functional relevance has been investigated.6–10 Coherent and incoherent feedforward motifs, for example, are known to determine the (non)monotonicity of input–output profiles.11,12 While an incoherent feedforward loop can provide fold-change detection13 and accelerate response time,14 a coherent feedforward loop can serve as a sign-sensitive delay element in regulatory networks.6 These studies suggest that the nature of interaction between the members of the pathway (i.e. being repressing or activating) and their network of interaction determines the response of the system to various inputs. Longer transcriptional cascades, with an ordered sequential chain of regulations, are also at the basis of many complex developmental processes.15 For instance, the transcriptional program of skeletogenic cell development in a sea urchin embryo includes several layers of regulation that correspond to developmental phases.16 Despite experimental advancements in understanding regulatory networks in such complex developmental processes, we lack a systematic approach towards understanding the functional features of long transcriptional cascades and how the addition of coherent and incoherent interlocked feedforward loops and changing the arrangement of interactions within the cascade affect its function. By analogy with the arrangement of intra-molecular interactions in proteins and nucleic acids, we define circuit topology and contact order for a transcriptional cascade.17–23 We propose that the arrangement of these interactions is an important topological property and put forward a mathematical model that explains the dynamics of each element and how various topological features can change the response of each element in the cascade. We study how different topologies can change the kinetics and steady-state level of the response. Most transcriptional factors are composed of multiple subunit components, e.g. dimers, and tetramers. The transcription factor gets fully active when these subunits bind to inducer molecules to regulate gene expression. The binding process usually reaches equilibrium within milliseconds for typical inducers. A useful phenomenological model that governs the reaction kinetics in the steady-state is the Hill function that captures cooperative behavior in a single exponent.24–26 When several transcription factors are chained to regulate their respective downstream genes, they form transcriptional cascades which are commonly found in developmental transcription networks.27 Long transcriptional cascades usually lead to longer response time for the downstream genes which occur in time scale of cell generations (can take up to hours). Therefore, we can safely assume that there is a separation of timescale between the binding process (reaches equilibrium in seconds), transcription and translation of target genes (take up to minutes), and the accumulation of protein products (take many minutes/hours).28 The cascade includes a linear chain of reactions that carry biochemical information received by its first component along its linear path to the last component. The components of the linear pathway can interact coherently and/or incoherently, i.e. every upstream element activates its neighboring downstream element (no backwards interaction). We used a bottom up approach for studying the role of topology: we start off by examining the properties of a simple chain with no out-of-chain interaction and then add interactions with simplest to the topologically more complex arrangements. In the end, we use our model to infer the dynamics of the developmental network for Bacillus subtilis spores and discuss how a similar mathematical approach can be used to study the dynamics of metabolic pathways.2 Methods
2.1 Dynamics of a linear pathway
The concentration of a protein in a population of cells can vary from cell to cell due to stochastic processes.29–31 If a gene is bound by a relatively large number of transcription factors, it exhibits more robust expression and is less prone to stochastic variations in expression. Here, we employ the widely used linear noise approximation (LNA)30,32–34 which allows rapid characterization of the stochastic properties of the cascade over large parameter regions. By using the LNA method, the reaction rates in the master equation are linearized and the steady-state solution becomes a multivariate Gaussian distribution. Thus, the marginal distributions for each element of the cascade can be described at the level of Gaussian fluctuations with the mean value for the number of proteins that is given by the steady-state solution to the deterministic model. This method has proven to be effective, especially in describing the dynamics of gene regulatory networks, where the mean expression level of each protein can be modelled with high accuracy by combining transcription and translation into one step.35–37 Thus, to describe the dynamics of each element in the pathway we use the following interpretation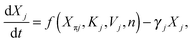 | (1) |
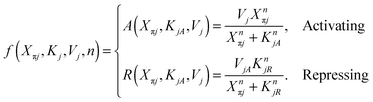 | (2) |
2.2 Topological measures
By analogy with the arrangement of contacts in a linear biopolymer,18 arrangement of biochemical interactions in an otherwise linear cascade is a topological property. Any two interactions can take one of the three arrangements, series (S), parallel (P), and cross (X). Another important measure of the arrangement of interactions is the average distance between the interacting partners, the so-called contact order in structural biology.19 The size of the cascade and the position of the interactions in the pathway are also important structural features that are examined along with circuit topology. For a cascade with an arbitrary number of interactions, the assignment protocol of circuit topologies can be applied to any pair of interactions leading to a complete characterization of the topology of pathways. Such classification of arrangements could, in principle, be implemented in any type of pathway. In the case of gene regulatory networks, the types of pairwise interactions correspond to feedforward loop motifs. A feedforward loop consists of three genes (A, B, and C) and three regulatory interactions. The most downstream element of the feedforward loop, e.g. C, is directly regulated by 2 other products A and B. The production of B, in turn, is regulated by A. While in a coherent feed-forward loop the regulation of B and C by A is of the same type (i.e. both activating or both repressing), in an incoherent loop the regulations are of opposite nature (i.e. one activating and one repressing). The distribution of cascade lengths in databases of transcriptional networks for S. cerevisiae,40 endomesoderm development in sea urchin,41 and Drosophila early development (pair-rule genes) demonstrates that transcriptional cascades can involve up to 8–9 genes (see ref. 27 for a review).3 Results
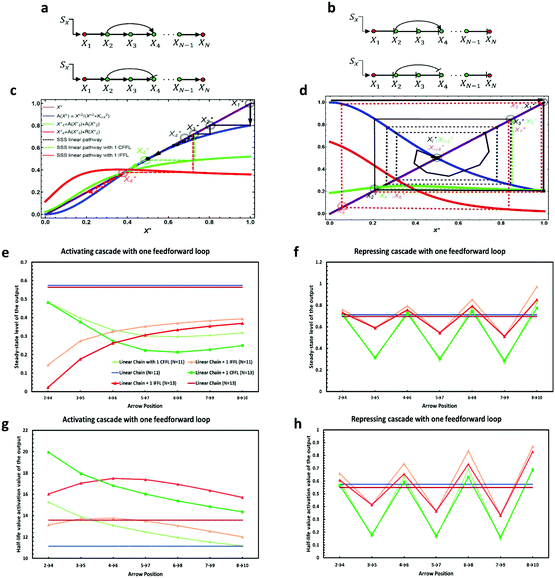
3.1 Properties of a linear pathway with one feed-forward loop
Consider a linear cascade of arbitrary length, N, with a linear chain of biochemical reactions consisting of one input signal Sx, which can be an inducer molecule that binds to protein X1 or a modification of X1 by a signal-transduction cascade, and a chain of transcription factor proteins {X1,X2,…,XN} that regulate one another. A constant input signal Sx of amplitude β is transduced through the pathway where it stimulates the first element, X1. As the level of X1 reaches half of its maximal, it effectively starts to regulate the second element, X2. The same chain of interactions regulate X3 up to XN. The basic properties of a linear activating/repressing cascade before increasing the complexity of interactions are worth discussing. To address the mean-field dynamics of the system using eqn (1) and (2), we assume, from now on, that all the interactions in the linear cascade are all of the same type (i.e. either activating or repressing Hill functions) with constant and equal degradation rates γj = γ, binding constants Kj = K, maximum expression levels Vj = V, and cooperativity coefficient n = 2 (i.e. transcription factors bind DNA as dimers). Fixing the cooperativity at other constant values greater than two has marginal effects compared to n = 2 (see ref. 34 for further discussion). Solving for the steady-state of the system, we find the following set of fixed points for the linear cascades: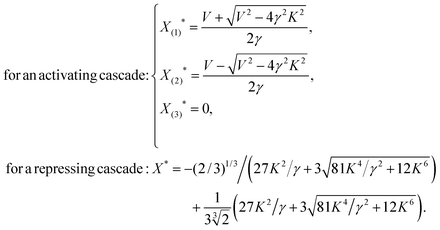 | (3) |
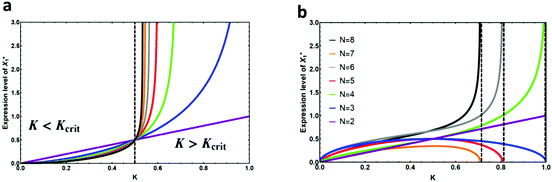
From eqn (3), we find that an activating cascade exhibits a saddle-node bifurcation and has three fixed points whereas a repressing cascade has only one stable fixed point. The critical protein binding constant, Kcrit = V/(2γ), sets the boundary between two distinct behaviors for the activating cascade (for detailed analysis see Appendix A, ESI†). (i) Decaying mode: for K > Kcrit, there is only one stable fixed point at X(3)* = 0, as given by eqn (3). In this parameter regime, the activation threshold for each element of the cascade is too high such that the input signal cannot transmit through the downstream elements (also see Fig. 3). Therefore, irrespective of the magnitude of the initial signal, the steady-state level of each element decreases as the signal transmits through the cascade until it eventually dies out as it reaches the most downstream gene. As a result, the output gene does not get activated and the cell is at a disadvantage. (ii) Bistable mode: for K < Kcrit, there are two stable fixed points at X(1)* and X(3)*, and one unstable fixed point at X(2)*. Depending on the strength of the input signal, the steady-state level of each element would either increase to reach a non-zero value (cell is not at a disadvantage), when SX > X(2)*, or decrease to zero (cell is at a disadvantage), when SX < X(2)*. Since in real biological systems there are always cell to cell variations in the production of each protein, for cells in which X* < X(2)*, the downstream genes cannot get activated which can be disadvantageous for them.
Note that in this scenario, there is a chance for the signal not to die out as it propagates further downstream and reaches the non-trivial fixed point X(1)*. (iii) Transition point: K = Kcrit defines the boundary between the first two modes of the cascade. By changing the maximum expression level, V, or degradation/dilution rate, γ, we can tune the transition point. For instance, by increasing V and/or decreasing γ, we can shift the threshold value up such that the transition from Bistable to Decaying mode becomes less likely. Thus, we can synthetically tune an activating cascade to ensure that all genes get activated. Such points of qualitative change in the behavior of signal-response profile has also been found in other types of biological networks.42–46 On the other hand, as eqn (3) suggests, a repressing cascade has only one stable fixed point. Therefore, given that the duration of the constant input signal is long enough to effectively initiate the repressing chain of regulations,28,47 regardless of the magnitude of the input signal, the steady-state expression level of the output always approaches a non-zero value. This implies that repressing cascades are more robust to fluctuations in the input signal and, thus, can be found more frequently in linear transcriptional cascades.48,49
This preliminary finding forms the basis for our analysis in the following sections regarding the role of topology in regulatory cascades. We now introduce one interlocked (in)coherent feedforward loop into the cascade by adding one extra interaction, i.e. an activating or a repressing regulation, to the linear cascade (see the curved arrows in Fig. 1a). We consider the behavior of the cascade near its transition point (K = Kcrit). By changing the position of the feedforward loop along the cascade, we measure the steady-state response of each element and the half-life time for the activation of the last element XN (i.e. output) as a function of the arrow position. We find that the kinetics and the steady-state response of the output for both cases with an extra activating and repressing interaction of length two, i.e. connecting a pair of elements through a feedforward loop, significantly depends on their positions in the cascades (see Fig. 1).
To explain the dependency of the steady-state level of the output on the curved arrow, we need to understand its effect on the steady-state value of intermediate nodes Xj*. The one-dimensional map to find the steady-state solution in this case is very similar to the one we found for a linear cascade, except for the fact that the regulating function for the doubly regulated node, m, where the (in)coherent feedforward loop acts, differs from others
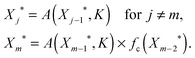 | (4) |
Note that all the interactions in the linear cascade are either activating, i.e. f(Xj−1*,KA) = A(Xj−1*,KA), or repressing i.e. f(Xj−1*,KA) = R(Xj−1*,KR), Hill functions and the extra regulation by the curved arrow, fc, can create an interlocked coherent or incoherent feedforward loop depending on whether it is activating A(Xj−1*,KA) or repressing R(Xj−1*,KR) the production of Xm. These two regulations should be multiplied together (AND gate) to get the steady-state level of Xm*.
Therefore, for an activating cascade, the steady-state expression level of each member of the pathway, Xj*, can be divided into two sub-groups: before the doubly regulated node, the steady-state of each element approaches the non-zero fixed point (given by eqn (3)). After the doubly regulated node (i.e. j ≥ m), the value of Xj* changes depending on the nature of interaction from the curved arrow. Consequently, the cascade may either maintain its initial non-zero steady-state or jump over the unstable fixed point and approach zero, i.e. the downstream elements will no longer get activated (see the green and red dotted lines in Fig. 1b) – size of the pathway N determines the number of times we apply the mapping rule in eqn (4). Therefore, an incoherent feedforward loop in the cascade has the ability to shut down the regulatory cascade which could potentially damage the cell function. By changing the position of the curved arrow, we can manipulate the “jump” in the steady-state. While having an incoherent feedforward loop in the upstream (e.g. X2 repressing X4) can have a dramatic impact on the fate of the output, i.e. repressing link in the upstream causes a significant decrease in the expression level of the output, a coherent feedforward loop can increase the expression of output to relatively higher amounts (given that the steady-state value of each element remains above the unstable fixed point). Fig. 1c and d show that placing the incoherent feedforward closer to downstream elements of the cascade (e.g. X8 regulating X10) makes close to no change in the steady-state and half-life time of the output. Our simulation results also show that for an activating cascade of particular size, there is an optimum position for the interlocked coherent feedforward loop to minimize the steady-state and maximize the delay in activation of the output (i.e. X5 activating X7).
On the other hand, a repressing cascade demonstrates a completely different behavior. Since there is only one stable fixed point for the cascade, the steady-state expression level of downstream elements would ultimately approach that fixed point. However, the extra feedforward loop introduces a “lag” in the steady-state response of each downstream element after the doubly regulated node. In other words, for a linear cascade with one coherent feedforward loop (Fig. 1b), the steady-state level of each element Xi* is equal to the steady-state level of Xi−2* of a regular linear cascade with no extra interaction (see the green and black dashed lines in Fig. 1d). Similarly, for a linear cascade with one incoherent feedforward loop, the steady-state level of Xi* would be the same as Xi−4* in a linear cascade (see the red dashed lines in Fig. 1d). This explains the ups and downs in the steady-state expression level of the output as the position of the feedforward loop changes along the cascade (see Fig. 1f). We can also see in Fig. 1f that the variations around the steady-state solution for a linear cascade (solid blue and red lines) are lower for a cascade with an incoherent feedforward loop than those with a coherent feedforward loop. The half-life activation time for the production of the output in a repressing cascade is much shorter compared to the activating cascade (see Fig. 1h). This suggests that long activating transcriptional cascades can lead to long response times for downstream elements while repressing cascades tend to respond with almost no delay. Therefore, our analysis suggests that long activating cascades can exhibit longer delays (on the order of cell generation) more reliably for biological processes such as cell differentiation which requires proteins that are produced in the mother cell to be used in the next generation of daughter cells.
3.2 What is the fate of an input signal as it transmits through a pathway with a certain circuit topology?
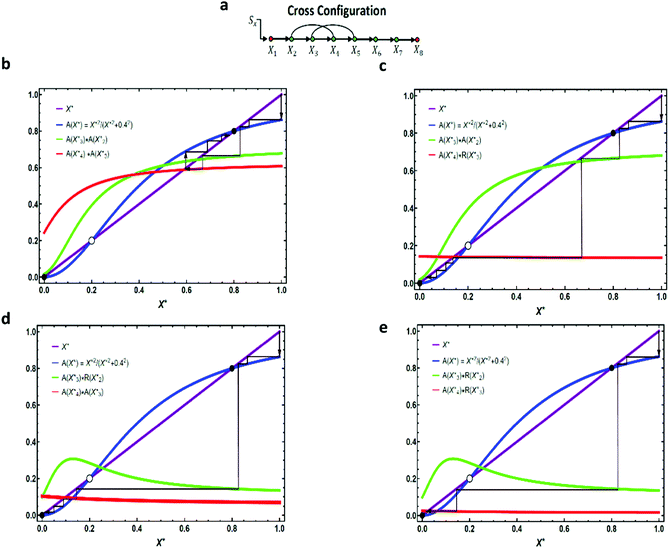
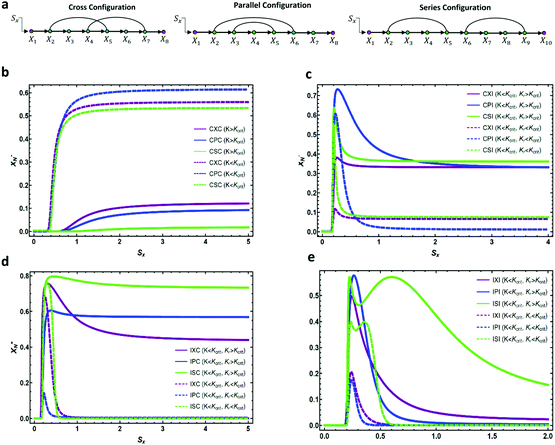
Having analyzed the properties of a linear cascade with one feedforward loop, we now have the means to study different circuit topologies. From now on, we only discuss the topological properties of an activating cascade – the same approach can be applied to study repressing cascades. In the previous section, we found how adding a coherent or incoherent feedforward loop to a linear cascade can change the response of the system to an external input (for a detailed analysis see Appendix B, ESI†). Similarly, for a linear cascade with two extra interactions, we can build two coherent and/or incoherent feedforward loops and depending on the arrangement of the two extra interactions, there can be three different topologies: (i) cross (X), (ii) parallel (P), or (iii) series (S). We can divide all the possible configurations into four classes: CαC, CαI, IαI, and IαC, where α denotes a specific circuit topology (i.e. X, P, or S) and the letter C(I) represents one coherent (incoherent) feedforward loop. To determine the average contact order, consider, for instance, one representation of IXC arrangement where X2 represses the production of X4, creating an incoherent feedforward loop of length two, and X3 activates the production of X5, creating a coherent feedforward loop of length two. This makes an average contact order of (2 + 2)/2 = 2. Here, we fix the contact order to two and study the steady-state and half-life time for one realization of a pathway with cross topology. A similar approach can be implemented to study the other two topologies (see Appendix C, ESI†).As we discussed in the previous section, the curved arrows can have a considerable influence on the fate of the input, especially when they are in the upstream. We consider an example of a cross configuration with X2 regulating X4 and X3 regulating X5 as shown in Fig. 2a. We find three possible scenarios for the bistable mode: (i) in CXC configuration (see Fig. 2b), both activating curved arrows will reduce the expression level of the intermediate elements compared to a normal linear cascade with no extra interaction. However, their effect is not considerable enough to change the fixed point of the system (i.e. no “jumping” over the fixed point occurs). Thus, the pathway will restore the input signal by approaching its non-zero stable fixed point. (ii) For CXI configuration (see Fig. 2c), the first curved arrow decreases the steady-state of X4, similar to case (i) (because the two pathways are identical up to this point), while the second arrow (repressing interaction) causes the steady-state level to drop significantly and switches the stable fixed point of the pathway. Consequently, the input signal will die out as it propagates downstream. (iii) For both IXC and IXI configurations (Fig. 2d and e), the scenarios look similar. The first repressing regulation changes the fixed point of the pathway, whereas the second curved arrow (either the activating or repressing interaction) only determines the magnitude by which the steady-state is going to drop. A similar analysis exploits the steady-state expression levels of the elements of the pathway with Parallel and Series topologies (see Appendix C, ESI†). Our simulations suggest that for CαI configurations, if the magnitude of the repressing interaction is not too strong, then downstream genes would still be able to get activated (see also Fig. S4b and d, ESI†). However, IαC and IαI configurations are less likely to activate downstream elements of the cascade.
3.3 Non-monotonic input–output profiles and the emergence of adaptive response in circuit topologies with incoherent feed-forward loops
Impulse responses and sustained responses are also key features of linear cascades. To study the monotonicity of the input–output profile for a certain circuit topology, we first examine the properties of a linear cascade of length N with no feedforward loop. In order to effectively activate/repress the output, XN, the adjacent upstream element XN−1 should reach half of its maximum expression level, i.e. when XN−1* = K the production rate of XN reaches f(XN−1* = K) = V/2. Since the cascade is linear, XN−1* is, in turn, regulated by XN−2*. Thus, for XN−1* to reach K, the expression level of XN−2* should satisfy the condition XN−1* = K = f(XN−2*). We can write a recursion relation for the regulation of each gene as a function of its adjacent upstream gene. Ultimately, we find a condition for the regulation of output XN* as a function of the input X1*. For an activating cascade, we have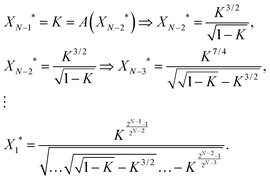 | (5) |
We were not able to find a closed form for the input–output profile of a repressing cascade. However, the results of our computer calculations can be found in Fig. 3. As demonstrated in Fig. 3a, the expression level of X1* that is needed to activate XN* gets exceedingly high for K > Kcrit, whereas it diminishes to lower values for K < Kcrit. This highlights the point that we made earlier about the “Decaying mode”, where it becomes exceedingly unlikely for a signal to propagate through the pathway with K > Kcrit, and “Bistable mode”, where the input signal can get amplified as it propagates through the downstream elements. Fig. 3b shows that there is a unique cut-off value for the protein binding constant, K, given N, beyond which XN−1 cannot effectively repress the production of XN (vertical dashed lines). It also demonstrates that the expression level of X1* required for repressing the output becomes exceedingly large for linear cascades of size N = 4, 6, and 8. This happens because for these cascades, the steady-state level of XN−1 is below the fixed point value of a repressing cascade, X(1)* (see eqn (3)). Thus, if the cut-off value of K is higher than X(1)*, it will be implossible for XN−1 to repress the production of the output.
Now, we examine the monotonicity of the input–output profile for three realizations of cross, parallel, and series topologies (see Fig. 4). Our numerical results indicate that for the CαC configuration with two coherent feedforward loops (Fig. 4b) the input–output profile is monotonic. We observe that for K > Kcrit, the response of the output is weaker than that for K < Kcrit as it is harder for the signal to activate downstream elements. We also note that when K > Kcrit, the response of the CPC pathway is strongest, whereas for K < Kcrit CXC has the strongest response. For CαIs with the first feedforward loop being coherent and the second one incoherent, the CPI pathway has the highest peak in the non-monotonic response (see Fig. 4c). While for KR > Kcrit the repressing interaction cannot get fully activated, i.e. the expression level of the output reaches a non-zero value as the amplitude of the signal increases, for KR < Kcrit the input–output profile performs an almost adaptive response where the expression level of the output settles at a low persistence amount. As demonstrated in Fig. 4d, the IαC category of pathways demonstrates a fully adaptive response for KR < Kcrit, i.e. the system's ability to respond to a change in the input stimulus and returning to its pre-stimulated output level, with ISC having the highest peak in the adaptive response. Comparing the adaptive response in Fig. 4c and d, we find that if the incoherent feedforward loop appears in the pathway before the coherent one, it has a stronger effect in controlling the adaptive behavior of the response. For IαI, all the circuit topologies perform an adaptive response with IPI and ISI having the highest peaks. Also for KR < Kcrit, the input–output profiles demonstrate lower peak amplitudes and faster decays. It is also important to note that for the ISI topology, the steady-state level of the intermediate element X5* (the first doubly regulated element) acts as an input to the second part of the pathway, hence, creating an input–output profile that has two peaks. The first one corresponds to the activation of the first incoherent feedforward loop by the input and the other corresponds to the activation of the second incoherent feedforward loop by the first one. This is one of the characteristic features of incoherent feedforward loops connected in Series which has been analyzed in regulatory networks.50 Therefore, we have shown that while some activating cascades with one incoherent feedforward loop can perform pulse-like responses, others can also produce sustained responses which make them more robust against cell-to-cell variations.
3.4 Time dependent input signal: which circuit topology is more robust to noise?
So far, we have only studied the response of a linear cascade to a constant input signal. However, in many biological systems, we often deal with time-varying signals which reflect the changes in the environmental conditions. Such systems are subject to extrinsic noise, in which the cellular capacity to produce proteins and the concentration of transcription factors that regulate a gene fluctuate over a certain period. The correlation time of such variations in production rates is often on the scale of a cell generation: that is, a cell with high production levels often tends to stay high for a cell cycle or more.51 Here, we take an approach similar to the work by Gomez-Uribe and collaborators52 in studying such systems in the deterministic regime. We study the response of a coherent and incoherent feedforward loop to an oscillatory input signal of the form Sx(t) = s0(1 + α![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin(ωt)). We further discuss what will happen if we introduce the second feedforward loop and change the circuit topology of the cascade. Although a deterministic sinusoidal signal does not exist in a real biological system, high frequency changes in the input can serve as fluctuations in the signal. For a signal with small variations around its baseline level (i.e. α
sin(ωt)). We further discuss what will happen if we introduce the second feedforward loop and change the circuit topology of the cascade. Although a deterministic sinusoidal signal does not exist in a real biological system, high frequency changes in the input can serve as fluctuations in the signal. For a signal with small variations around its baseline level (i.e. α![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin(ωt) ≪ 1), the time varying response of the cascade can be linearized about its steady-state by doing first-order Taylor series expansion such that the dynamics of the variations is governed by linear and time-independent coefficients (see Appendix D for analytical results, ESI†). Therefore, we can approximate |δXi|, the amplitude of variations in each element, around the steady-state solution Xi*. By defining a gain, gij, for the ith element being regulated by its parent element j (depends on the first derivative of the production rate) and a cut-off frequency ωci (depends on the degradation/dilution rate), we analyze how the system responds to the changes in input frequency. For instance, in a simple feedforward loop with 3 elements {X1, X2, X3}, where X3 is the doubly regulated element, the amplitude of variations in the response of each element can be found (see Appendix D for the derivation and full expression of each element, ESI†):
sin(ωt) ≪ 1), the time varying response of the cascade can be linearized about its steady-state by doing first-order Taylor series expansion such that the dynamics of the variations is governed by linear and time-independent coefficients (see Appendix D for analytical results, ESI†). Therefore, we can approximate |δXi|, the amplitude of variations in each element, around the steady-state solution Xi*. By defining a gain, gij, for the ith element being regulated by its parent element j (depends on the first derivative of the production rate) and a cut-off frequency ωci (depends on the degradation/dilution rate), we analyze how the system responds to the changes in input frequency. For instance, in a simple feedforward loop with 3 elements {X1, X2, X3}, where X3 is the doubly regulated element, the amplitude of variations in the response of each element can be found (see Appendix D for the derivation and full expression of each element, ESI†):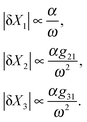 | (6) |
Therefore, the amplitude of variations in the output around its steady-state solution decays as 1/ω2 for high frequency changes in the input singal. In other words, the feedforward loop acts as a low pass filter to the input signal with high frequency. For lower frequencies in the input, the variations would be larger for proteins with smaller degradation rates (i.e. smaller values of ωc). This property of feedforward loops has also been highlighted in the work by Guantes and collaborators.53 The variations in each element also depend linearly on the amplitude of oscillations in the input α, as well as the gain from the parent element(s) which directly regulates them. Note that the amplitude of variation in the doubly regulated element, X3, to the first leading term in ω, only depends on g31 which changes with the expression level of X1. This indicates that the noise propagation in a feedforward loop with high frequency input only depends on the parent element with the most variation in the amplitude. In other words, when X3 is both regulated by X2 and X1 (parent elements), the amplitude of variation in X3 is most dominated by the parent element X1 which is closer to the source and has a higher variation amplitude. Therefore, cascades where the most upstream elements are interacting with the most downstream elements are more susceptible to noise propagation. In the case of three different circuit topologies demonstrated in Fig. 4a, the amplitude of variation for the doubly regulated elements is:
(i) Cross configuration
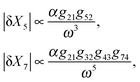 | (7) |
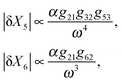 | (8) |
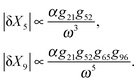 | (9) |
We find that while the doubly regulated elements in cross and series configurations exhibit the same dependency on ω (eqn (7) and (9)), parallel configuration shows a relatively weaker dependency (eqn (8)). The reason why parallel configuration is a weaker low-pass filter is that there are long-range interactions between the upstream and downstream elements, i.e. the upstream element X2 regulates X6 which is almost at the end of the pathway. This topological property of the Parallel configuration makes it less robust to noise propagations. For a slowly varying input signal (ω ≪ ωc1, ωc2, ωc3), the characteristic frequency of each element is higher than the input signal. Thus, the signal is perceived as a constant input for each member of the cascade. Thus, each element has enough time to reach its steady-state expression level before it starts to sense the oscillations of the input signal (see Fig. 5b). On the other hand, if the oscillations in the input are too fast (ω ≫ ωc1, ωc2, ωc3), the dynamics of each element is too slow to sense the rapid oscillations in the input (see Fig. 5a). Consequently, the variations decay to zero for very large oscillations (see eqn (7)–(9)). Although our approximation is only suitable for small amplitudes and is expected to hold for small perturbations around the mean, our experience with the simulations was that it provides a good guide for describing output for all amplitudes. This analysis shows that by adjusting the pathway parameters γ and K we can make our linear pathway robust to fluctuations of high frequency and each circuit topology demonstrates a unique low-pass filtering property with parallel topologies being the most susceptible one to noise. We have shown that, in addition to all these features, they are also able to reduce signal fluctuations. This further justifies their ubiquity in biological networks, and perhaps accounts in part for the robustness of living systems.
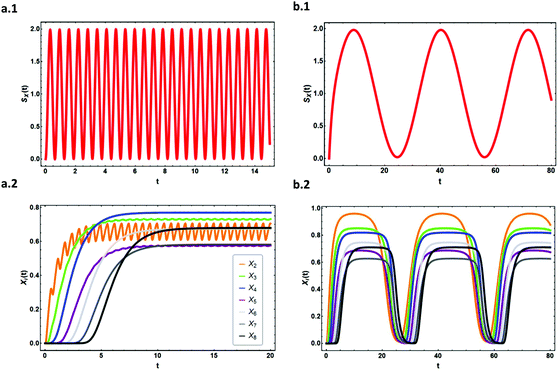 | ||
| Fig. 5 The effect of large amplitude noise propagation on the expression level of each element in a linear activating cascade with cross topology given in Fig. 4a. The expression level of each element is demonstrated as a function of time for (a.1) and (a.2) ω = 10, α = 10, s = 1 and for (b.1) and (b.2) ω = 0.1, α = 1, and s = 1. The expression level of the output X8 for (a) is ≈0.68, for (b) is ≈0.70, and for a cascade with constant input signal is ≈0.70. Thus, there is a minor change in the steady-state expression level of the output when the noise frequency is high (regardless of the amplitude α) compared to a constant input (i.e. low-pass filtering property of the linear cascade). | ||
4 A linear cascade with series configuration in B. Subtilis
Here, we provide an example of a regulatory gene cascade that guides the B. Subtilis spore.54 We identify the underlying circuit topologies of the cascade and try to understand its dynamics based on the behavior of individual circuit topologies. When B. Subtilis bacteria are under conditions of nutrient limitation, they stop growing and start to differentiate into spores and can remain dormant for extended periods of time. When a bacterium makes a spore, it switches on a new set of proteins which involves hundreds of genes. The genes are turned on and off to carry out specific stages in the formation of the spore.28,54 As demonstrated in Fig. 5, the transcriptional network that regulates sporulation is an activating cascade which is made of several coherent and incoherent feedforward loops and includes a subset of parallel configurations.As we discussed in Section 3.1, this activating cascade should be in the bistable mode (i.e. has a non-zero steady-state fixed point) so that all the elements of the cascade are guaranteed to get activated (as long as the input signal is persistent). We also know that there should be a well-defined delay between the activation of each element in an activating cascade so that each gene is activated at a particular time. Following the approach in Sections 3.1 and 3.2 (see eqn (3) and (4)), we can find the steady-state level of each element:
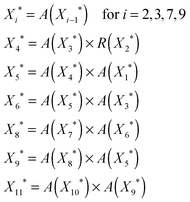 | (10) |
We also know that IPC configuration in Fig. 5b is capable of producing a sustained response to input signal (see Section 3.3) which is essential for maintaining the robustness of the cascade (Fig. 6).
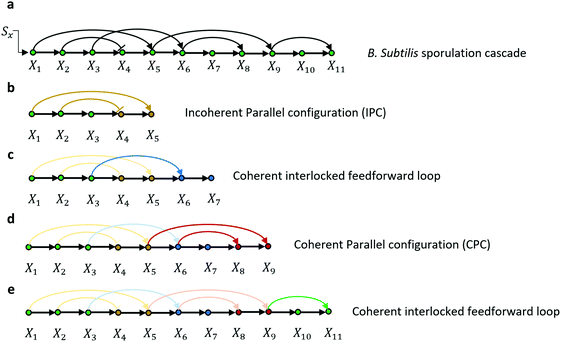 | ||
| Fig. 6 (a) A transcriptional cascade for the development of Bacillus subtilis spores. Note that the original cascades include multiple sub-branches that represent groups of tens of hundreds of genes.54 We only selected the longest activating cascade to study the kinetics and steady-state response of the output and removed all the other sub-branches out of the cascade. (b–e) Are the underlying topological substructures in the cascade. | ||
5 Dynamics of metabolic pathways
One of the other important categories of pathways are metabolic networks. The mathematical description of the dynamics of metabolic pathways is provided by means of a set of ordinary differential equations which represent the inflow and outflow rates to the production of metabolites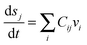 | (11) |
6 Discussion
Linear cascades are common in many biological systems. From G-protein cascade-mediating phototransduction63 and MAP kinase cascades in S. cerevisiae,64 to gene regulatory cascades in the flagellar motor development of E. coli.65 More complex regulatory architectures, such as the one in developmental programs, include regulators that are ordered in layers where proteins from one layer control the ones in subsequent layers.48,49 Such patterns are observed in transcriptional networks during sea urchin development16,66 and Bacillus subtilis sporulation development54 (also see ref. 66 and 67 for a review). A cascade-like network topology entails an inherent temporal order of regulation events and provides robustness both to spurious input signals and to noise in the rates of protein production.48,68 In this work, by analogy with the arrangement of intra-molecular interactions in proteins and nucleic acids, we defined three distinct circuit topologies for an otherwise linear transcriptional cascade and systematically constructed a mathematical framework to address some of their key function-topology features. Following a bottom-up approach, we first found the steady-state expression level for each member of the cascade and identified two types of responses to a constant (persistent) input signal, namely the decaying mode and the bistable mode. Applying the mean-field approximation, we found a critical binding constant above which it becomes exceedingly difficult for the signal to propagate through the cascade. Below this critical value, the system can assume a non-zero steady-state value. We then examined how the system can switch from one mode to another as we add coherent and/or incoherent feedforward loops into the cascade. We found that, in the bistable mode, a switch from a non-zero to zero steady-state expression level occurs most effectively if interlocked incoherent feedforward loops appear closer to upstream elements. Understanding this switch-like transition in pathways with incoherent feedforward loops would also help us better understand the effect of paradoxical components in transcriptional circuits,69 where one element of the pathway is responsible for both activating and repressing the expression level of a downstream element (or promoting proliferation and death rate), and the conditions under which homeostasis can be achieved.70 We also examined the input–output profile of cascades with different circuit topologies and various combinations of coherent and incoherent feedforward loops. We found that in the bistable mode, cascades with at least one incoherent feedforward loop can perform adaptive responses with the IαoC category of pathways demonstrating the sharpest transient peak and the most sensitive adaptive response. We argued that the strength of the repressing interaction governs the non-monotonic behavior and determines the quality of the adaptive response. We also found an analytical expression for the activation/repression threshold of the output as a function of the input source for a linear cascade of arbitrary length. Our results also indicated that cross and series configurations demonstrate strong low-pass filtering dynamics, while parallel configurations are not strong low-pass filters due to a long-range interaction between upstream and downstream elements, which allows noise to propagate even further down into the pathway. The cut-off frequency of each element, which depends on the degradation/dilution rate, can provide a versatile module to tune the noise-filtering property.52 In the end, we analyzed the topological features of a transcriptional cascade in B. subtilis spore development. We believe that the same approach can be used to understand the dynamics of other transcriptional cascades. Our mathematical approach can also be implemented in studying systems with positive or negative feedback,45,71i.e. multistable biological systems that switch between discrete states, and systems with extensive crosstalk between pathways.72,73 Understanding the role of topology in cellular networks helps us better understand how one specific change in the set of interactions can shift the dynamics from one behavior to another and how regulatory cascades can bound the fluctuations in the input signal. This could also be of great value in designing effective therapeutic strategies to treat diseases and to modify cellular processes with simple engineering principles. Motivated by recent advancements in synthetic biology to manipulate biological entities, we believe that the time is ripe for designing systems that aid in the development and interpretation of analytical models with increasing complexity and discover additional constraints on design principles for biological networks.Conflicts of interest
There are no conflicts of interest to declare.References
- T. R. Sorrells and A. Johnson, Cell, 2015, 161, 714–723 CrossRef CAS PubMed.
- A. Blais and B. Dynlacht, Genes Dev., 2005, 19, 1499–1511 CrossRef CAS PubMed.
- E. Davidson and M. Levin, Gene regulatory networks, 2005 Search PubMed.
- L. M. Angerer and R. C. Angerer, Curr. Top. Dev. Biol., 2003, 53, 159–198 CrossRef CAS PubMed.
- B. Aldridge, J. Burke, D. Lauffenburger and P. Sorger, Nat. Cell Biol., 2006, 8, 1195–1203 CrossRef CAS PubMed.
- A. Z. S. Mangan and U. Alon, J. Mol. Biol., 2003, 334, 197–204 CrossRef PubMed.
- H. Jeong, S. Mason, A.-L. Barabási and Z. Oltvai, Nature, 2001, 411, 41–42 CrossRef CAS PubMed.
- D.-S. Lee, J. Park, K. Kay, N. Christakis, Z. Oltvai and A.-L. Barabási, Proc. Natl. Acad. Sci. U. S. A., 2008, 105, 9880–9885 CrossRef CAS PubMed.
- S.-H. Yook, Z. Oltvai and A.-L. Barabási, Proteomics, 2004, 4, 928–942 CrossRef CAS PubMed.
- A. Mashaghi, A. Ramezanpour and V. Karimipour, Eur. Phys. J. B, 2004, 41, 113–121 CrossRef CAS.
- R. van Wijk, S. Tans, P. ten Wolde and A. Mashaghi, Sci. Rep., 2015, 5, 11376 CrossRef PubMed.
- S. Kaplan, A. Bren, E. Dekel and U. Alon, Mol. Syst. Biol., 2008, 4, 203 CrossRef PubMed.
- L. Goentoro, O. Shoval, M. Kirschner and U. Alon, Mol. Cell, 2009, 36, 894–899 CrossRef CAS PubMed.
- S. Mangan, S. Itzkovitz, A. Zaslaver and U. Alon, J. Mol. Biol., 2006, 356, 1073–1081 CrossRef CAS PubMed.
- E. Davidson, The regulatory genome: gene regulatory networks in development and evolution, Academic Press, 2010 Search PubMed.
- P. Oliveri, Q. Tu and E. Davidson, Proc. Natl. Acad. Sci. U. S. A., 2008, 105, 5955–5962 CrossRef CAS PubMed.
- A. Mugler, S. Tans and A. Mashaghi, Phys. Chem. Chem. Phys., 2014, 16, 22537–22544 RSC.
- A. Mashaghi, R. van Wijk and S. Tans, Structure, 2014, 22, 1227–1237 CrossRef CAS PubMed.
- D. Baker, Nature, 2000, 405, 39–42 CrossRef CAS PubMed.
- A. Mashaghi and A. Ramezanpour, RSC Adv., 2015, 5, 51682–51689 RSC.
- A. Mashaghi and A. Ramezanpour, Soft Matter, 2015, 11, 6576–6585 RSC.
- N. Nikoofard and A. Mashaghi, Nanoscale, 2016, 8, 4643–4649 RSC.
- S. Verovšek and A. Mashaghi, Frontiers in Applied Mathematics and Statistics, 2016, 2, 6 CrossRef.
- A. Hill, Biochem. J., 1913, 7, 471 CrossRef CAS PubMed.
- H. McAdams and A. Arkin, Annu. Rev. Biophys. Biomol. Struct., 1998, 27, 199–224 CrossRef CAS PubMed.
- Q. Zhang, S. Bhattacharya and M. Andersen, Open Biol., 2013, 3, 130031 CrossRef PubMed.
- N. Rosenfeld and U. Alon, J. Mol. Biol., 2003, 329, 645–654 CrossRef CAS PubMed.
- U. Alon, An introduction to systems biology: design principles of biological circuits, CRC Press, 2006 Search PubMed.
- N. R. I. Lestas, J. Paulsson and G. Vinnicombe, IEEE Trans. Autom. Control, 2008, 53, 189–200 CrossRef.
- J. Paulsson, Nature, 2004, 427, 415–418 CrossRef CAS PubMed.
- G. Karlebach and R. Shamir, Nat. Rev. Mol. Cell Biol., 2008, 9, 770 CrossRef CAS PubMed.
- J. Elf and M. Ehrenberg, Genome Res., 2003, 13, 2475–2484 CrossRef CAS PubMed.
- A. Mugler, E. Ziv, I. Nemenman and C. Wiggins, Syst. Biol., 2009, 3, 379–387 CAS.
- E. Ziv, I. Nemenman and C. Wiggins, PLoS One, 2007, 2, e1077 Search PubMed.
- T. Gardner, C. Cantor and J. Collins, Nature, 2000, 403, 339–342 CrossRef CAS PubMed.
- J. Hasty, D. McMillen, F. Isaacs and J. Collins, Nat. Rev. Genet., 2001, 2, 268–279 CrossRef CAS PubMed.
- M. Elowitz and S. Leibler, Nature, 2000, 403, 335–338 CrossRef CAS PubMed.
- P. Smolen, D. Baxter and J. Byrne, Bull. Math. Biol., 2000, 62, 247–292 CrossRef CAS PubMed.
- S. Mangan and U. Alon, Proc. Natl. Acad. Sci. U. S. A., 2003, 100, 11980–11985 CrossRef CAS PubMed.
- T. Lee, N. Rinaldi, F. Robert, D. Odom, Z. Bar-Joseph, G. Gerber, N. Hannett, C. Harbison, C. Thompson, I. Simon and J. Zeitlinger, Science, 2002, 298, 799–804 CrossRef CAS PubMed.
- E. Davidson, J. Rast, P. Oliveri, A. Ransick, C. Calestani, C.-H. Yuh, T. Minokawa, G. Amore, V. Hinman, C. Arenas-Mena and O. Otim, Science, 2002, 295, 1669–1678 CrossRef CAS PubMed.
- M. Laurent and N. Kellershohn, Trends Biochem. Sci., 1999, 24, 418–422 CrossRef CAS PubMed.
- J. Ferrell and E. Machleder, Science, 1998, 280, 895–898 CrossRef CAS PubMed.
- M. Thomson and J. Gunawardena, Nature, 2009, 460, 274–277 CrossRef CAS PubMed.
- D. Angeli, J. Ferrell and E. Sontag, Proc. Natl. Acad. Sci. U. S. A., 2004, 101, 1822–1827 CrossRef CAS PubMed.
- E. Ozbudak, M. Thattai, H. Lim, B. Shraiman and A. V. Oudenaarden, Nature, 2004, 427, 737–740 CrossRef CAS PubMed.
- M. Wall, M. Dunlop and W. Hlavacek, J. Mol. Biol., 2005, 349, 501–514 CrossRef CAS PubMed.
- S. Hooshangi, S. Thiberge and R. Weiss, Proc. Natl. Acad. Sci. U. S. A., 2005, 102, 3581–3586 CrossRef CAS PubMed.
- N. Rappaport, S. Winter and N. Barkai, Theor. Biol. Med. Modell., 2005, 2, 22 CrossRef PubMed.
- S. Ishihara, K. Fujimoto and T. Shibata, Genes Cells, 2005, 10, 1025–1038 CrossRef CAS PubMed.
- N. Rosenfeld, J. Young, U. Alon, P. Swain and M. Elowitz, Science, 2005, 307, 1962–1965 CrossRef CAS PubMed.
- C. Gomez-Uribe, G. Verghese and L. Mirny, PLoS Comput. Biol., 2007, 3, e246 Search PubMed.
- R. Guantes, J. Estrada and J. Poyatos, PLoS One, 2010, 5, e12314 Search PubMed.
- S. Wang, B. Setlow, E. Conlon, J. Lyon, D. Imamura, T. Sato, P. Setlow, R. Losick and P. Eichenberger, J. Mol. Biol., 2006, 358, 16–37 CrossRef CAS PubMed.
- R. Heinrich, S. Rapoport and T. Rapoport, Prog. Biophys. Mol. Biol., 1978, 32, 1–82 CrossRef.
- M.-A. Albert, J. Haanstra, V. Hannaert, R. Van, F. Opperdoes, B. Bakker and P. Michels, J. Biol. Chem., 2005, 280, 28306–28315 CrossRef CAS PubMed.
- M. Rizzi, M. Baltes, U. Theobald and M. Reuss, Biotechnol. Bioeng., 1997, 55, 592–608 CrossRef CAS PubMed.
- V. Singh, C. Kaur, V. Chaudhary, K. Rao and S. Chatterjee, Sci. Rep., 2015, 5, 12906 CrossRef CAS PubMed.
- M. Savageau, Addison Wesley Publication, 1976 Search PubMed.
- H. Kacser, J. Burns and D. Fell, The control of flux, 1995 Search PubMed.
- B. Mulukutla, A. Yongky, S. Grimm and P. D. W.-S. Hu, PLoS One, 2015, 10, e0121561 Search PubMed.
- B. Ingalls, Internet. [cited at p. 117], 2013.
- R. Heinrich, B. Neel and T. Rapoport, Mol. Cell, 2002, 9, 957–970 CrossRef CAS PubMed.
- B. Schoeberl, C. Eichler-Jonsson, E. Gilles and G. Müller, Nat. Biotechnol., 2002, 20, 370–375 CrossRef PubMed.
- S. Kalir, J. McClure, K. Pabbaraju, C. Southward, M. Ronen, S. Leibler, M. Surette and U. Alon, Science, 2001, 292, 2080–2083 CrossRef CAS PubMed.
- E. Davidson, Curr. Opin. Genet. Dev., 2009, 19, 535–540 CrossRef CAS PubMed.
- N. Yosef and A. Regev, Cell, 2011, 144, 886–896 CrossRef CAS PubMed.
- M. Thattai and A. van Oudenaarden, Biophys. J., 2002, 82, 2943–2950 CrossRef CAS PubMed.
- Y. Hart and U. Alon, Mol. Cell, 2013, 49, 213–221 CrossRef CAS PubMed.
- Y. Hart, S. Reich-Zeliger, Y. Antebi, I. Zaretsky, A. Mayo, U. Alon and N. Friedman, Cell, 2014, 158, 1022–1032 CrossRef CAS PubMed.
- B. Novák and J. Tyson, Nat. Rev. Mol. Cell Biol., 2008, 9, 981–991 CrossRef PubMed.
- I. Fraser and R. Germain, Nat. Immunol., 2009, 10, 327–331 CrossRef CAS PubMed.
- M. Natarajan, K.-M. Lin, R. Hsueh, P. Sternweis and R. Ranganathan, Nat. Cell Biol., 2006, 8, 571–580 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c7cp02671d |
| This journal is © the Owner Societies 2017 |