Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
2-Thiouracil intersystem crossing photodynamics studied by wavelength-dependent photoelectron and transient absorption spectroscopies†
José A.
Sánchez-Rodríguez‡
a,
Abed
Mohamadzade‡
a,
Sebastian
Mai‡
 b,
Brennan
Ashwood‡
b,
Brennan
Ashwood‡
 c,
Marvin
Pollum
c,
Philipp
Marquetand
c,
Marvin
Pollum
c,
Philipp
Marquetand
 b,
Leticia
González
b,
Leticia
González
 *b,
Carlos E.
Crespo-Hernández
*b,
Carlos E.
Crespo-Hernández
 *c and
Susanne
Ullrich
*a
*c and
Susanne
Ullrich
*a
aDepartment of Physics and Astronomy, University of Georgia, Athens, GA 30602, USA. E-mail: ullrich@physast.uga.edu
bInstitute of Theoretical Chemistry, Faculty of Chemistry, University of Vienna, Währinger Straße 17, 1090 Vienna, Austria. E-mail: leticia.gonzalez@univie.ac.at
cDepartment of Chemistry and Center for Chemical Dynamics, Case Western Reserve University, 10900 Euclid Avenue, Cleveland, Ohio 44106, USA. E-mail: carlos.crespo@case.edu
First published on 12th June 2017
Abstract
Single-atom substitution within a natural nucleobase—such as replacing oxygen by sulfur in uracil—can result in drastic changes in the relaxation dynamics after UV excitation. While the photodynamics of natural nucleobases like uracil are dominated by pathways along singlet excited states, the photodynamics of thiobases like 2-thiouracil populate the triplet manifold with near unity quantum yield. In the present study, a synergistic approach based on time-resolved photoelectron spectroscopy (TRPES), time-resolved absorption spectroscopy (TRAS), and ab initio computations has been particularly successful at unraveling the underlying photophysical principles and describing the dissimilarities between the natural and substituted nucleobases. Specifically, we find that varying the excitation wavelength leads to differences between gas-phase and condensed-phase experimental results. Systematic trends are observed in the intersystem crossing time constants with varying excitation wavelength, which can be readily interpreted in the context of ab initio calculations performed both in vacuum and including solvent effects. Thus, the combination of TRPES and TRAS experiments with high-level computational techniques allows us to characterize the topology of the potential energy surfaces defining the relaxation dynamics of 2-thiouracil in both gas and condensed phases, as well as investigate the accessibility of conical intersections and crossings, and potential energy barriers along the associated relaxation coordinates.
Introduction
Canonical nucleobases found in DNA and RNA possess inherent photoprotective mechanisms against harmful UV radiation, featuring primarily ultrafast excited-state relaxation to the ground state, either directly or through intermediate singlet excited states.1–11 Thiobases—structurally modified nucleobases where a sulfur atom substitutes the oxygen atom in a carbonyl group—have revealed how single-atom substitution can drastically affect the accessibility of these relaxation pathways.7,12–21 Molecules such as 6-thioguanine17,22,23 4-thiothymine,13,14,16,18,24 and 2-thiocytosine21 exhibit femtosecond intersystem crossing (ISC) dynamics that result in nearly unity triplet yields. The population of the triplet state prepares a highly reactive molecule, which by itself, or through diffusional encounter with molecular oxygen to generate singlet oxygen,18,22,23 can damage biomolecules within the cell.25–27 Hence, not only how the triplet states are populated in these thiobases, but also the magnitude of their triplet-state lifetimes, are of special interest in phototherapeutic applications.18,20,28–30Besides the 6-thioguanine, 4-thiothymine, and 2-thiocytosine monomers, other thiobases such as 2-thiouracil also populate the reactive triplet state in high yields and on an ultrafast time scale. However, the dynamics responsible for ISC to the triplet state and then again back to the ground state are not fully elucidated, and are the subject of the present study. Early experiments with 2-thiouracil in solution19,31 provided evidence for the involvement of the 1nπ* state in the ultrafast population of the 3ππ* state, and a triplet decay lifetime of 70 ns in acetonitrile was measured by Vendrell-Criado et al.32 Recently, Yu et al.33 reported the first investigation of the excited-state dynamics of 2-thiouracil in the gas phase using time-resolved photoionization. The results revealed an ultrafast (<100 fs) lifetime, which was assigned to internal conversion from the 1ππ* state to the 1nπ* state, a second lifetime of 775 fs associated with the population of the triplet manifold, and a third lifetime of 203 ps, which was assigned to the decay of the 3ππ* state back to the ground state. The repopulation of the ground state in few hundreds of picoseconds in the gas phase was proposed to be associated with a small energy barrier (ca. 0.2 eV) that needs to be overcome in order to access the triplet–singlet intersection seam and a large spin–orbit coupling of 130 cm−1 at this intersection.33
A number of computational studies have also investigated the molecular mechanisms responsible for the efficient ISC of 2-thiouracil. The first study, by Cui and Fang,34 who employed the CASPT2//CASSCF method (computing energies with CASPT2 based on geometries obtained with CASSCF), reported three possible pathways from the initially excited S2(1ππ*) state to the lowest triplet state T1(3ππ*). The proposed pathways are S2(1ππ*) → S1(1nπ*) → T1(3ππ*) (path I), S2(1ππ*) → T2(3nπ*) → T1(3ππ*) (path II), and S2(1ππ*) → T3(3nπ*) → T2(3nπ*) → T1(3ππ*) (path III), as sketched in Fig. 1. In their computations, Cui and Fang34 imposed planarity of the 2-thiouracil molecule in the optimization of the excited-state stationary points. This motivated less-restrictive follow-up calculations by Gobbo and Borin,35 who identified paths I and II as probable relaxation pathways. More recently, a study by some of us36 highlighted that most of the stationary and intersection points of 2-thiouracil exhibit significant out-of-plane distortions contrary to the presumptions of Cui and Fang.34 Hence, Mai et al.36 concluded that while the general relaxation pathways of Cui and Fang (paths I to III) correctly involve the relevant excited states, the details of the relaxation pathways (i.e., energies, energy gaps, barriers, involvement of specific structures) are not reliable. Using MS-CASPT2 for both energies and geometries,36 the authors showed that S2 → S1 → T2 → T1 is in fact the primary relaxation pathway. Noteworthy, they also clarified36,37 that this pathway corresponds to 1ππ* → 1nπ* → 3ππ* (as in path I), as the 3ππ* state is the second-lowest triplet state (the T2) at the singlet–triplet crossing after temporarily switching order with the 3nπ* state. That study also showed that this crossing seam between the 1nπ* and 3ππ* states is easily accessible, and that the large spin–orbit couplings (SOCs) of up to 150 cm−1 can induce population transfer to the triplet state. The magnitude of the SOCs can be explained by the change of orbital type in the 1nπ* → 3ππ* transition (following the El-Sayed rule38) and the heavy-atom effect of the sulfur atom. Furthermore, the particular topology of the excited-state potentials disfavors direct relaxation to the ground state, explaining the near-unity ISC yield of 2-thiouracil.19 These findings, derived from static calculations, were more recently confirmed by MS-CASPT2-based dynamics simulations,37 which showed trajectories relaxing primarily along path I, although path II was also observed. According to the kinetic model of ref. 37, the 1ππ* → 1nπ* step occurs within less than 100 fs (τ1 = 59 ± 12 fs), followed by the 1nπ* → 3ππ* ISC step with a lifetime (τ2) of approximately 400 fs. It was also shown that the process of relaxation towards the S1(1nπ*) minimum is accompanied by strong out-of-plane motion of the sulfur atom.37
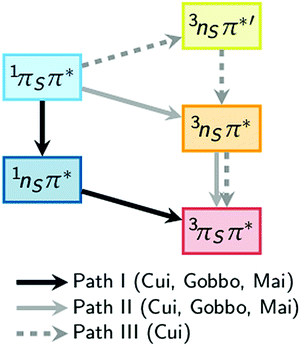 | ||
| Fig. 1 Comparison of theoretical pathways for the population of the excited triplet state as calculated by Cui and Fang,34 Gobbo and Borin,35 and Mai et al.36 | ||
In the present work, we show interesting changes of the above-mentioned lifetimes when varying the excitation wavelength in our gas-phase (time-resolved photoelectron spectroscopy, TRPES) and condensed-phase (time-resolved absorption spectroscopy, TRAS) measurements. In particular, we find a strikingly different behavior between dynamics in the gas phase and solution. Based on ab initio simulations, we explain these findings with the presence of energy barriers to access conical intersections and singlet–triplet crossing points.
Experimental details
Time-resolved photoelectron spectroscopy setup
The apparatus used in the gas-phase experiments, including a femtosecond laser system, a gaseous molecular beam source, and a magnetic bottle photoelectron spectrometer, have been described in detail in ref. 39–43.In order to transfer 2-thiouracil (Sigma Aldrich, ≥98%) into the gas phase, the sample was placed in a quartz holder and heated to 210 °C. The continuous gas molecular beam was transported to the source vacuum chamber with a helium carrier gas while being doubly skimmed. In the ionization region of the spectrometer the molecular beam and the UV femtosecond pump pulse and time-delayed probe pulse intersect, with the pump and probe beams being focused by two separate 50 cm lenses to spatially overlap at a small angle.
All pump pulses (249, 259.9, 271, 283 and 291.5 nm) were generated using a Coherent Inc. OPerA optical parametric amplifier (OPA). The probe pulse of 329 nm was produced from a Coherent Inc. traveling-wave OPA (TOPAS-C). The probe beam wavelength was selected due to its low absorbance in 2-thiouracil,44 thus reducing the possibility of obtaining undesirable probe–pump signal. In order to promote a 1 + 2′ pump–probe scheme for ionization, the pump pulse energy was kept at 1.5–1.7 μJ per pulse and the probe pulse energy at 11–15 μJ per pulse.
A 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 50 mixture of 1,3-butadiene and helium was used to conduct the timing calibrations. The Gaussian cross-correlation function showed a full width at half maximum of around 200 fs, and defined the position of zero pump–probe delay. The photoelectron energy spectra were calibrated using the known ionization potentials and vibrational features of 1,3-butadiene.45
50 mixture of 1,3-butadiene and helium was used to conduct the timing calibrations. The Gaussian cross-correlation function showed a full width at half maximum of around 200 fs, and defined the position of zero pump–probe delay. The photoelectron energy spectra were calibrated using the known ionization potentials and vibrational features of 1,3-butadiene.45
For each excitation wavelength, short-range 2D TRPES data were recorded with equal step size of 25 fs for a pump–probe delay up to 4 ps. The contributions that make up the overall TRPES signal were deconvoluted with a global analysis program written in Labview based on simultaneous fitting of the spectra and associated decay dynamics. The algorithm uses standard sequential rate equations with numerical convolution. Three individual contributions were necessary to accurately fit the measured data, such that the residual signal was negligible and random (see the ESI† in Fig. S1 for the systematic fitting residuals obtained with only two constants). Time traces of individual contributions are generated by integration over all electron energies. The dynamics of the long-lived (tens to hundreds ps) contribution were characterized in a separate long-range TRPES scan with unequal step size that extends beyond 200 ps pump–probe delay. Using a sequential triple exponential decay function convoluted with a Gaussian instrument response function, a time constant for the long (ps) decay was extracted in OriginPro from a global fit to the energy-integrated short- and long-range scans and used in the 2D fits described above.
Femtosecond-to-microsecond time-resolved absorption setup
TRAS was used to study the decay of the triplet state of 2-thiouracil in acetonitrile. The laser and spectrometer setup was described in significant detail in previous publications.19,46 In brief, a Ti:Sapphire oscillator seeds a chirped pulse regenerative amplifier (Coherent Libra-HE). The amplifier generates 4 mJ, 100 fs pulses at 800 nm with a 1 kHz repetition rate, which were used to pump an optical parametric amplifier (OPA, TOPAS, Quantronix/Light Conversion). A small fraction of the fundamental beam was split off prior to the OPA and focused through a constantly-moving 2 mm CaF2 crystal to generate a broadband probe pulse (320–710 nm). The spectrometer (Helios, Ultrafast Systems, LLC) employs a mechanical delay stage to adjust the time it takes the probe pulse to reach the sample. The broadband probe pulses were split into two fractions. One beam passes through the sample (2 mm path length) to probe the transient signals, while the other serves to correct for changes in the white light continuum throughout the experiment. The pulses were focused into optical fibers leading to CMOS detection units. Generation of the reference signal comes via a chopper wheel, which blocks every other pump pulse, providing an alternating sequence of spectra with and without sample excitation, and thus providing ΔA transient absorption data. The OPA was tuned to excitation wavelengths of 268, 290, and 316 nm. Excitation pulses were set to an intensity of 1 μJ at the sample using a neutral density optical filter in order to minimize cross-phase modulation effects as well as sample degradation.The nanosecond transient absorption experiments make use of an electronically-triggered photonic crystal fiber for probe light generation in the spectral range from ∼375 to 800 nm (Eos, Ultrafast Systems, LLC) with a time resolution of 400 ps and a temporal window of up to 120 μs.46,47 This light source is conveniently coupled to our femtosecond transient absorption spectrometer described above, which allows the use of identical experimental conditions, signal detection, and data collection.
For these experiments, samples were prepared in acetonitrile at a concentration of 0.6 mM, unless stated otherwise, and under N2-saturated conditions to minimize diffusional quenching of the long-lived signals by molecular oxygen which may become relevant on ns-to-μs time scales. N2-Saturated solutions were purged for 30 min prior and blanketed with N2 for the course of the experiment. Air-saturated solutions, of ca. 0.5 mM concentration of 2-thiouracil in acetonitrile, were used during the collection of the ultrafast dynamics at excitation wavelengths of 268 and 290 nm. A concentration of 1.2 mM was used for ultrafast experiments performed with excitation wavelength of 316 nm. For all transient absorption experiments, solutions were continuously stirred using a Teflon stir bar, and samples were replaced with fresh solutions before the change in absorbance reached 5% to avoid any contamination of the transient signals by the excitation of possible photoproducts.
A homemade software (Labview, National Instruments, Inc.) was used for data collection. Approximately 30 kinetic traces in the probe spectral range from ca. 630 to 710 nm were averaged from the transient absorption band of the triplet state and fitted to a single-exponential decay function, convoluted by the instrument response function of 400 ps using Igor Pro 6.36.19,46
Computational details
In order to rationalize the observed rates for ISC to the ground state, we performed quantum chemical calculations on the MS-CASPT2(12,9)/cc-pVDZ (multi-state complete active space second-order perturbation theory) level of theory.48,49 We optimized two T1 minima and two T1/S0 minimum-energy crossing points50 of 2-thiouracil, using numerical gradients and the polarizable continuum model (PCM)51 to account for the acetonitrile solvent. Because T1 → S0 ISC is a slow process, the PCM charges were computed self-consistently with the T1 state. The energy profiles shown below were obtained with single-point calculations on geometries obtained by linear interpolation in internal coordinates. All computations were performed with MOLCAS 8.0,52 using no IPEA shift61 and an imaginary level shift of 0.2 a.u. The optimized coordinates are given in the ESI.†Results and discussion
Fig. 2 presents the UV absorption spectrum of 2-thiouracil in the gas phase44 (green) and in acetonitrile solution19,31 (blue). The green arrows mark the pump and probe wavelengths employed in the TRPES measurements, whereas the blue arrows indicate the pump wavelengths used in the TRAS experiments. Excitation occurs primarily to the lowest-energy absorption band, which ab initio calculations36 assign to the bright 1πSπ6* state and, towards the high-energy side of the band, the 1πSπ2* state (these are the S2 and S4 states at the Franck–Condon (FC) point); the energetic positions of these states are indicated in the figure. Note that from here on we adopt the state nomenclature from ref. 36 in order to distinguish between the several nπ* and ππ* states of 2-thiouracil. Accordingly, the bright 1πSπ6* and 1πSπ2* states correspond to electron promotion from the π orbital localized at the sulfur atom into two different ring π* orbitals: π6* localized significantly at carbon C6 (i.e., the π* orbital of the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C double bond) and π2* at C2 (π* orbital of the C
C double bond) and π2* at C2 (π* orbital of the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) S double bond), as shown in Fig. 2 (bottom).36 The weak absorption toward longer wavelengths is associated with the 1nSπ2* state (S1), a transition with small oscillator strength originating from the non-bonding sulfur orbital.
S double bond), as shown in Fig. 2 (bottom).36 The weak absorption toward longer wavelengths is associated with the 1nSπ2* state (S1), a transition with small oscillator strength originating from the non-bonding sulfur orbital.
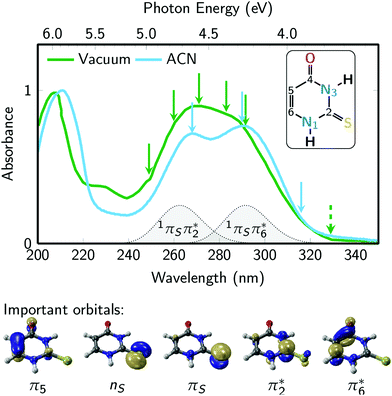 | ||
| Fig. 2 2-Thiouracil absorption spectrum44 in the gas phase (green) and acetonitrile (ACN, blue) with an absorption band centered around 275 nm wavelength, which is due to the bright S2(1πSπ6*) and S4(1πSπ2*) states. The green arrows represent the pump wavelengths centered at 249, 259.9, 271, 283 and 291.5 nm and the green dashed arrow represents the 329 nm probe wavelength used in the TRPES experiments. The blue arrows represent the pump wavelengths (268, 290, and 316 nm) used in the TRAS experiments, which monitored the dynamics in the 320 to 700 nm probe range. The inset shows the molecular structure of 2-thiouracil's most stable tautomer,53,54 with the atomic numbering also shown. Important frontier orbitals of 2-thiouracil are shown below the spectra. These five orbitals are involved in all relevant excited states (labelled as 1nSπ2*, 1πSπ2*, 1πSπ6*, 3nSπ2*, 3πSπ2*, 3π5π6*). | ||
Role of the excitation wavelength in the excited-state dynamics in gas phase
The 2-thiouracil TRPES results shown in Fig. 3 are arranged from top to bottom in order of increasing excitation wavelengths with the corresponding data (column 1) and fit results presented along each row (total 2D fit in column 2; individual 2D contributions in columns 3–5; energy-integrated time traces in columns 6 and 7). All color maps are plotted as a function of electron binding energy versus pump–probe delay. The electron binding energies are calculated by subtracting the measured photoelectron kinetic energies from the total photon energy of the 1 + 2′ multiphoton excitation–ionization process.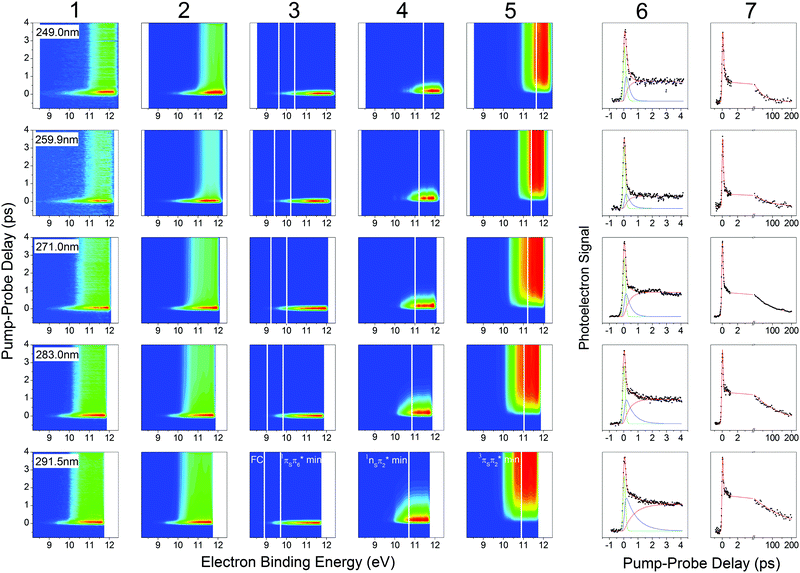 | ||
| Fig. 3 TRPES and time traces of 2-thiouracil pumped at 249 nm (first row), 259.9 nm (second row), 271 nm (third row), 283 nm (fourth row) and 291.5 nm (fifth row) and probed at 329 nm in a 1 + 2′ process. TRPES signal, fit, and individual contributions are presented in the first five columns. The vertical white lines indicate calculated total binding energies for different geometries (FC, 1πSπ6* min, 1nSπ2* min, 3πSπ2* min) from ref. 33, shifted accordingly in the first four rows. Column 6 shows the energy-integrated signals of the first five columns, i.e. the signal (dots), fit (red solid line) and individual contributions (green, blue, pink solid lines) for the short scan. Column 7 shows the signal (dots) and fit (red solid line) for a separate long-range scan, which was used to extract the long-lived decay time constant. The 291.5 nm data set in the bottom row was previously published in ref. 33. | ||
Analysis of the photoelectron spectra relies on ionization correlations between the neutral excited and ionic states. The basic procedure has been described in detail in ref. 33 for the TRPES measurement at 291.5 nm excitation, which is reproduced here in the bottom row of Fig. 3. A brief summary of essential information is given below. Photoionization from all relevant excited states (1nSπ2*, 1πSπ2*, 1πSπ6*, 3nSπ2*, 3πSπ2*, 3π5π6*) will preferentially occur into the lowest ionization band (IP1),55 which is due to two close-lying ionic states with the hole in either the sulfur n or π orbital.56 The change in ionization energy along the relaxation path was previously characterized by ab initio calculations.33 Taking the destabilization of the ionic states and the stabilization of the neutral states (i.e., vibrational energy gain) during relaxation into account, photoelectron signals are expected at the total electron binding energies indicated as solid white lines in Fig. 3. For 291.5 nm excitation, these correspond to 8.9 eV for ionization from the FC region, 9.7 eV and 10.7 eV from the 1πSπ6* and 1πSπ2* minima, respectively, and between 10.9 eV and 10.1 eV for ionization from two different minima (3πSπ2*, 3π5π6*) in the triplet manifold. This information provides the basis for identification of the electronic excited states participating in the three-step relaxation process. Column 3 displays the short-lived TRPES signal following excitation to the bright 1πSπ* states and the subsequent relaxation towards the minimum of the 1πSπ6 state. The observed broad photoelectron band from ionization into IP1 (FC) and IP1 (1πSπ6* min) confirms this assignment. An approximately 1 eV shift of the photoelectron band towards higher electron binding energies in column 4 is in agreement with the calculated increase in IP1 for ionization from the 1nSπ2* minimum (IP1 (1nSπ2* min)) plus vibrational energy gain, and the TRPES signal is therefore assigned to the 1nSπ2*. No notable shift of the TRPES signal is observed between columns 4 and 5, suggesting the assignment to one of the two 3ππ* states (3πSπ2* or 3π5π6*), which were predicted to occur at similar electron binding energies as the 1nSπ2* state.56 We therefore propose internal conversion from the 1πSπ6* to the 1nSπ2* followed by ISC to the 3ππ* states as the dominant path for relaxation.
In a simplified picture, we assume a Δν = 0 propensity rule, such that any vibrational excitation in the electronically excited states is carried into the cationic state upon photoionization. As shorter excitation wavelengths are employed, photoexcitation to the 1πSπ6* (S2) or 1πSπ2* (S4) states leads to population of these states with increasing vibrational excitation, which according to our assumption leaves the photoelectron kinetic energy (Ekin) unaffected. Correspondingly, we observe a shift of the photoelectron bands towards higher electron binding energy (Ebind = Eexc + 2Eprobe − Ekin) with increasing excitation energy. The expected shifts are calculated relative to the 291.5 nm data set described above and indicated by solid white lines throughout Fig. 3. The effect becomes most visible when comparing the TRPES measurements with 291.5 nm (∼4.25 eV) and 249 nm (∼4.98 eV) excitation, where the difference in vibrational excitation amounts to ∼0.7 eV. Looking at the TRPES contributions in columns 3, 4 and 5, the onset of each photoelectron band is observed to shift between 0.5–1 eV with this change in excitation wavelengths. Due to the good agreement with the expected value and the absence of any other significant wavelength-dependent changes in the TRPES spectra, we conclude that relaxation primarily proceeds along the proposed 1πSπ6* → 1πSπ2* → 3ππ* pathway for all excitation wavelengths employed in this study. For shorter excitation wavelengths, as mentioned above, it is also conceivable that the second bright state (1πSπ2*) is initially excited, but it can be assumed that this state internally converts to the lower 1πSπ6* state and subsequently to the 1nSπ2* within the temporal resolution of the experiments, as given by the fitted constant τ1.
Table 1 collates all extracted time constants for the three-step relaxation process sorted by increasing excitation wavelength. The time constants τ1, τ2, and τ3 are associated with the TRPES contributions plotted in columns 3, 4, and 5, respectively. A general trend can be observed, where excitation with higher photon energy results in faster relaxation dynamics for τ2 and τ3. For all wavelengths, the first time constant τ1 is ultrafast (<100 fs) and within our Gaussian instrument response function. The second time constant τ2 ranges from ca. 200 to 800 fs and the third constant τ3 from ca. 50 to 200 ps.
| Pump wavelength (nm) | Pump energy (eV) | τ 1 (fs) | τ 2 (fs) | τ 3 (ps) |
|---|---|---|---|---|
| a Assigned to internal conversion from the 1πSπ6* to 1nSπ2* state. b Assigned to intersystem crossing from the 1nSπ2* state to the triplet manifold. c Assigned to the decay of the lowest-energy triplet state. | ||||
| 249.0 | 4.98 | 85 | 207 | 48.1 |
| 259.9 | 4.77 | 67 | 285 | 85.6 |
| 271.0 | 4.58 | <50 | 333 | 109 |
| 283.0 | 4.38 | <50 | 544 | 142 |
| 291.5 | 4.25 | <50 | 775 | 203 |
Comparing our time constants to the dynamics studies of Mai et al.,37 a good agreement between theory and experiments is observed. According to their mechanism, the presence of a 1πSπ6*/1nSπ2* conical intersection close to the 1πSπ6* minimum promotes ultrafast (<100 fs) internal conversion following excitation to the bright 1πSπ6* state. The slight increase in τ1 at shorter excitation wavelengths may be attributable to population of the higher-lying 1πSπ2* state and consequently a longer time to populate the 1nSπ2* state via the 1πSπ6*. Importantly, the state switch to 1nSπ2* induces changes in the geometry of 2-thiouracil, like out-of-plane puckering of the C2 atom and pyramidalization of the thiocarbonyl group, which take hundreds of femtoseconds to reach the 1nSπ2* minimum. At that point, population transfer to the 3πSπ2* state can occur after surmounting a small energy barrier (0.05–0.09 eV36) to reach the 1nSπ2*/3πSπ2* intersection seam. This barrier is possibly the reason for the observed pump-wavelength dependence of the ISC time constant. At shorter pump wavelengths, it is also conceivable that a minor fraction of the population takes other ISC routes, e.g., 1πSπ2* → 3nSπ2* → 3πSπ2*, as observed in the dynamics simulations of Mai et al.37 These additional ISC routes would also contribute to the observed increase of the ISC rate.
The third time constant τ3 is associated with ISC from the lowest adiabatic triplet potential energy surface, which features two distinct minima arising from the 3πSπ2* and 3π5π6* triplet states, back to the ground state. The associated decay time of tens to hundreds of picoseconds may be unexpectedly fast, but is theoretically supported by the presence of only a small energy barrier (0.2 eV) at the 3πSπ2*/S0 crossing point and the magnitude of the SOCs (130 cm−1) between the triplet state and the ground state.33 In contrast, as discussed in a previous work,33 the natural bases uracil and thymine show triplet lifetimes of >1 ns due to much smaller SOCs (∼2 cm−1) and larger energy barriers (∼0.4 eV).33 Like for τ2, the presence of an energy barrier to reach the triplet–singlet intersection seam could be the reason for the observed strong excitation wavelength-dependence of τ3.
Collectively, geometric changes of the molecule and the energy barriers to access the crossing seams play an important role in its ability to reach crossing points between excited states. Photoexcitation at shorter excitation wavelengths results in highly vibrationally excited molecules, leading to large-amplitude out-of-plane vibrations, including the carbon puckering and sulfur pyramidalization modes necessary for the ISC processes, and allows surmounting the relevant barriers, as described above. This reasoning can explain the systematic trend in time constants observed in the TRPES data.
Role of the excitation wavelength in the ultrafast excited-state dynamics in solution
The gas-phase results indicate that the magnitude of the ISC lifetimes to populate the triplet state or to repopulate the ground state decrease by a factor of four as the excitation wavelength is decreased from 291.5 to 249 nm (4.25 to 4.98 eV). It is proposed that this decrease is due to a higher probability of the population to overcome the calculated energy barriers to access the 1nSπ2*/3πSπ2* and the 3πSπ2*/S0 intersection seams. Recent experimental and computational studies19,21,31,33–37 suggest that the electronic relaxation mechanism of 2-thiouracil in solution is similar to that in the gas phase, which motivated further TRAS studies for direct comparison. In this section, we present the effects of varying the excitation wavelength on the ultrafast (i.e., sub-ns) dynamics of 2-thiouracil in solution, whereas the effects of excitation wavelength on the triplet decay to the ground state are postponed to the next section.Fig. 4 shows the transient absorption contour plots, the decay associated spectra (DAS), kinetic traces at selected probe wavelengths, and the corresponding fitting curves for 2-thiouracil in acetonitrile upon excitation at 268, 290, and 316 nm. Lifetimes obtained from a global fit analysis of the broadband data using a two-component sequential model plus a constant offset (see ESI† for details) are presented in Table 2. The black DAS is present at time zero and has been previously assigned to the 1nSπ2* state,31 but may also capture some residual absorption of the very short-lived 1πSπ* states. The black DAS subsequently evolves to the red spectrum with τsolv1, which further evolves to a constant offset spectrum (in blue) with τsolv2. The latter spectrum does not decay within the 200 ps time window used in the fs-TRAS experiments and was previously identified as the absorption spectrum of the long-lived 3ππ* state of 2-thiouracil in acetonitrile.19,31 Its ns decay dynamics will be discussed separately in the next section.
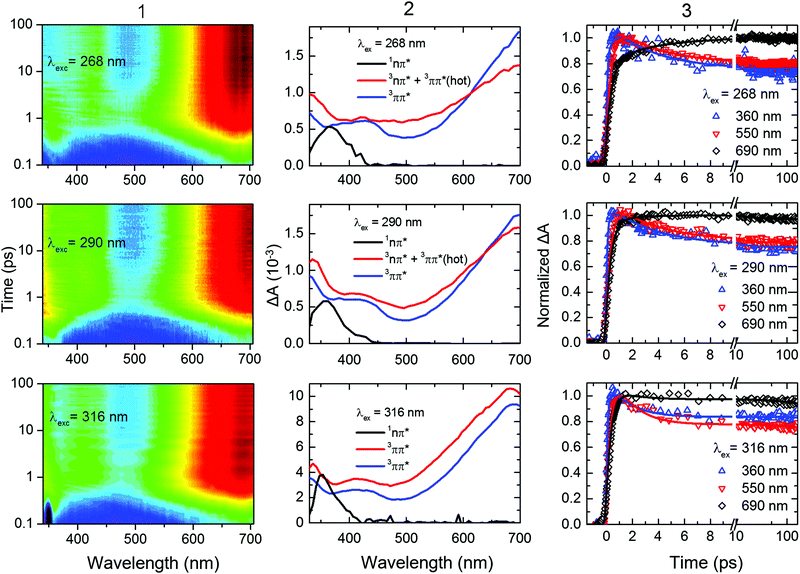 | ||
| Fig. 4 (Column 1) Contour plots of the multidimensional sub-ns TRAS data collected for 2-thiouracil in acetonitrile following excitation at the specified wavelengths. For clarity and completeness, the experimental transient absorption data is shown in Fig. S2 in the ESI.† The data was globally fitted to a two-component sequential kinetic model plus a constant offset, producing the decay associated spectra (DAS, Column 2) and the kinetic traces shown at representative probe wavelengths (Column 3). The black DAS spectrum is present at time zero and evolves to the red spectrum with τsolv1, which further evolves to an offset (spectrum in blue) with τsolv2. These lifetimes are gathered in Table 2. In the bottom middle panel, the change in amplitude between the blue and red DAS (both assigned to the 3ππ* state) is due triplet self-quenching (see main text for details). | ||
| λ ex (nm) |
τ
solv1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) a (fs) a (fs) |
τ solv2 (ps) |
τ
solv3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) d (ns) d (ns) |
|---|---|---|---|
| a Assigned to a combination of internal conversion from the 1πSπ6* to 1nSπ2* state and intersystem crossing to the triplet manifold. b Assigned to 3nπ* and vibrational cooling in the T1 state following 268 and 290 nm excitation. c Assigned to triplet self-quenching following 316 nm excitation. d Triplet decay lifetimes measured in a separate experiment (see below) for a 2-thiouracil concentration of 0.6 mM; reported uncertainties are twice the standard error obtained from global analyses of at least two independent data sets of experiments at each excitation wavelength. | |||
| 268 | 440 ± 30 | 3.7 ± 0.2b | 73 ± 10 |
| 290 | 380 ± 30 | 3.5 ± 0.2b | 69 ± 4 |
| 316 | 330 ± 40 | 5.5 ± 0.7c | 296 ± 23 |
Inspection of Fig. 4 and Table 2 shows subtle, but noticeable spectral and temporal changes in the excited-state dynamics of 2-thiouracil in solution as the excitation wavelength is varied (all spectral changes mentioned in the following correspond to a decrease in excitation wavelength). The spectral changes may be more conveniently visualized in the normalized DAS shown in Fig. S3 in the ESI.† The DAS show that the spectrum of the 1nSπ2* state (black spectrum) broadens and slightly redshifts. Similarly, the intermediate spectrum depicted in red broadens and its absorption maximum redshifts from ca. 682 to ≥700 nm (see transient absorption spectra in Fig. S2, ESI†). The maximum of the 3ππ* state spectrum depicted in blue also redshifts slightly. Upon excitation at 316 nm, the intermediate spectrum in red decays across the entire spectral probe window to the spectrum assigned to the 3ππ* state (blue spectrum). Conversely, as the excitation wavelength is decreased from 316 nm to 290 or 268 nm, the redshift of the intermediate absorption spectrum in red leads to an apparent increase in absorbance in the spectral range from 625 to 700 nm before reaching the spectrum of the 3ππ* state. The redshifting and broadening of these two DAS suggest that the excited-state absorption may be occurring from high-energy parts of the corresponding potential energy surfaces. In terms of the lifetimes, a slight increase in the magnitude of τsolv1 is observed with a decrease in excitation wavelength (see also Fig. 5), whereas the magnitude of τsolv2 also changes (Table 2).
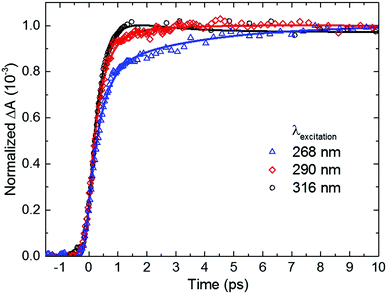 | ||
| Fig. 5 Dependence of the rate of triplet state population on excitation wavelength for 2-thiouracil in acetonitrile. Kinetic traces were taken at a probe wavelength of 690 nm, near the absorption maximum of the triplet state. For easier inspection, only the initial 10 ps time window of the dynamics is shown (see Fig. 4, right panel for an extended time window). | ||
Based on the discussion above and the assignment of the first and second DAS (black and red in Fig. 4), we assign τsolv1 to the 1πSπ6* → 1nSπ2*(hot) → 1nSπ2* → 3πSπ2* process,19,31 thus this constant is approximately equivalent to a combination of τ1 and τ2 of the TRPES experiments. The slight increase in the magnitude of τsolv1 and the broadening in the first DAS may be due to increased vibrational energy in the 1nSπ2* state, as vibrational cooling dynamics in an electronic state exhibits longer cooling times and broader electronic absorption spectra as the excitation energy is increased.57 Hence, the slowdown in τsolv1 with decreasing excitation wavelength can be understood as due to the vibrational energy redistribution (intramolecular, intermolecular, or both) being the rate-limiting step. However, another possibility is that the change in τsolv1 may be due to excitation of the higher-energy 1πSπ2* state in addition to (or at the expense of) the 1πSπ6* state. As shown in ref. 36 and 37, population in 1πSπ2* needs to overcome a small energy barrier before internal conversion to the 1nSπ2* state can occur (in contrast to population in the 1nSπ6* state), which could also explain the increase in the magnitude of τsolv1. If so, the observed broadening in the 1nSπ2* state spectrum could alternatively be explained by the absorption of the 1πSπ2* and/or 1πSπ6* states in the same spectral probe region that the 1nSπ2* state absorbs. Calculations of the absorption spectra of these states reported in the ESI† (Fig. S4) lend support to this proposition.
The spectral and temporal changes associated with τsolv2 as the excitation wavelength is decreased are more challenging to interpret. Upon 316 nm excitation, a uniform decay of absorbance from the red to the blue DAS is seen across the entire spectral window (Fig. 4). This decay process has been previously31 assigned to ground-state repopulation due to triplet self-quenching of 2-thiouracil molecules that aggregated in the ground state prior to excitation.19,31,58 In other words, a fraction of the triplet state population decays to the ground state by triplet self-quenching during τsolv2 when excitation is done at 316 nm. On the other hand, for excitation at 268 and 290 nm, an increase in absorbance at probe wavelengths of ca. ≥625 nm is observed in going from the second DAS (red spectrum) to the third DAS (blue), such that the latter DAS reaches the triplet absorption maximum at around 700 nm. Taking into consideration all the experimental and computational data available to date,31,33–37 we assign τsolv2 upon 268 or 290 nm excitation to vibrational cooling dynamics in the triplet state—analogous to 2-thiothymine.59 The narrowing of the transient absorption spectra during this lifetime supports this assignment. The different observations when excitation is performed at 290 or 268 nm versus at 316 nm can be explained by the different amount of vibrational energy in the triplet state. Additionally, we remark that a fraction of the excess vibrational energy may also redistribute intra-molecularly, in which case it could be used to overcome the energy barrier between the triplet minimum and the ground state intersection seam. This latter statement is explored in more detail in the next section from both experimental and computational perspectives.
Role of the excitation wavelength in the triplet state decay lifetime in solution
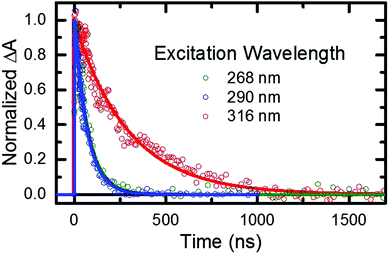
As stated in the previous section, any fraction of the excess excitation energy that accumulates intra-molecularly in the triplet state may in principle be used to overcome the calculated energy barrier between the triplet minimum and the ground state intersection seam.33,36,37 If so, an increase in the rate of triplet state decay back to the ground state may be observed, similar to that reported above in the gas phase. Hence, nanosecond TRAS experiments monitoring the decay of the triplet state of 2-thiouracil were performed in acetonitrile at multiple excitation wavelengths, in order to provide more insights into this possibility.From the fitting of the decay traces (see Fig. 6), it is apparent that triplet state decay in solution is three orders of magnitude slower than in gas phase. Moreover, the decay of the triplet state (τsolv3 in Table 2) is fivefold faster following excitation at 268 or 290 nm than at 316 nm. These experimental observations support the idea that an energy barrier between the triplet minimum and the ground state intersection seam also exists in solution.
PCM-MS-CASPT2(12,9)/cc-pVDZ calculations (Fig. 7) evidence that an energy barrier does indeed exist between the triplet minimum and the intersection seam with the ground state in acetonitrile. As shown in Fig. 7, the magnitude of the energy barrier increases by ∼40%, from 0.20 eV in vacuum to about 0.28 eV in acetonitrile, which partially explains the much slower triplet state decay in solution. Furthermore, the calculations predict that the lowest triplet surface has two minima, with the second triplet minimum (3π5π6*) being slightly lower in energy than the 3πSπ2* minimum by ca. 0.1 eV in acetonitrile. The 3π5π6* minimum is connected to a second T1/S0 intersection seam (3π5π6*/S0), where carbon atom C5 is strongly displaced from the molecular plane. This intersection seam is analogous to the one found in the natural nucleobases thymine and uracil,33 but its high energy and negligible SOCs mean that decay at this seam will not be competitive with decay at the 3πSπ2*/S0 seam. Hence, ISC to the ground state should always involve the 3πSπ2*/S0 intersection, independent of the minimum to which the population has settled during the vibrational cooling process. Population trapped in the lower-energy 3π5π6* minimum will therefore have to overcome an effective barrier of 0.36 eV to undergo ISC to the ground state. We think that this theoretical prediction can satisfactorily explain the observation that excitation at 316 nm leads to an ISC lifetime of ca. 300 ns, whereas excitation at shorter wavelengths than ca. 308 nm32 results in an ISC lifetime of ca. 70 ns (see Fig. 6 and Table 2). Excitation at 316 nm leads to trapping of population (τsolv3 ∼ 300 ns) in the 3π5π6* minimum, whereas excitation at wavelengths shorter than 308 nm may provide enough excess vibrational energy to settle in the 3πSπ2* minimum. Since the 3πSπ2* minimum is predicted to access the T1/S0 crossing more effectively than the 3π5π6* minimum (Fig. 7), excitation at shorter wavelengths can populate the 3πSπ2* minimum more effectively, leading to a faster decay of the triplet state population. If this interpretation of the experimental results holds true, then the DAS assigned to the lowest-energy triplet state in Fig. 4 could represent a weight-averaged linear combination of the spectra of the 3πSπ2* and the 3π5π6* minima, particularly as the excitation energy is increased. This could explain the subtle, but noticeable spectral changes in the DAS assigned to the lowest-energy triplet state with excitation energy (see the normalized DAS in Fig. S3 in the ESI†).
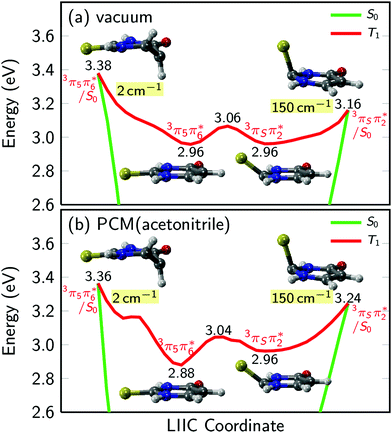 | ||
| Fig. 7 Potential energy profiles of the lowest triplet state of 2-thiouracil in vacuum and acetonitrile. Numbers in labels give the energy in eV above the ground state minimum, numbers shaded in yellow give the magnitude of SOCs at the crossing points. In vacuum and solution, the lowest triplet potential energy surface has two minima, arising from the 3πSπ2* and 3π5π6* states, respectively. The minima are separated by a small barrier and are each connected to a T1/S0 crossing point. The results are computed with MS-CASPT2(12,9)/cc-pVDZ as in ref. 37. For panel (b), the PCM charges were computed in equilibrium with the T1 state. | ||
Excitation-wavelength-dependent dynamics: gas-phase versus condensed-phase
As explained above, the excited-state dynamics of 2-thiouracil exhibits a striking dependence on excitation wavelength. In both gas and condensed phases, a decrease in excitation wavelength allows for population of higher-lying singlet states and for the accumulation of excess vibrational energy in the lowest-energy singlet state (1nSπ2*). Interestingly, the excess vibrational energy in the 1nSπ2* state apparently modulates the rate of intersystem crossing in the gas and solution phases differently. In the gas phase, more excitation energy accelerates ISC to the triplet manifold as population in the 1nSπ2* can more easily overcome the energy barrier to the 1nSπ2*/3πSπ2* intersection seam. In solution, it appears that the rate-limiting step of the experimentally-measured ISC lifetime (τsolv1, which combines the following processes: 1πSπ6* → 1nSπ2*(hot) → 1nSπ2* → 3πSπ2*) is the dissipation of excess vibrational energy in the 1nSπ2* state (either by intramolecular or intermolecular redistribution, or both), instead of overcoming the energy barrier to the 1nSπ2*/3πSπ2* intersection seam, as is the case in the gas phase. This supposition can satisfactorily explain the observation that while ISC in the gas phase occurs more rapidly with decreasing excitation wavelength, in the condensed phase ISC (τsolv1) slightly slows down. In other words, while the ISC lifetime in the gas phase is primarily modulated by the amount of excess vibrational energy available to overcome the relevant energy barrier, in solution, the ISC lifetime is primarily modulated by the rate of vibrational energy redistribution in the 1nSπ2*(hot) state. As remarked above, vibrational dynamics in an electronic state usually exhibit longer lifetimes as the excitation wavelength is decreased.57The triplet state decay to the ground state occurs more rapidly with decreasing excitation wavelength in both the gas and condensed phases. However, this dependence is bimodal (τsolv3 = 300 ns with λex = 316 nm and τsolv3 = 70 ns when λex ≤ 308 nm) in solution, whereas in gas phase τ3 depends continuously on the excitation wavelength. On the one hand, Fig. 7 shows that 0.2 eV are needed to reach the 3πSπ2*/S0 crossing from either of the calculated T1 minima in the gas phase, and this barrier can be more easily overcome as more excess vibrational energy is available. This process leads to the trend observed for the triplet decay reported in Table 1. On the other hand, the transfer of excess vibrational energy to the solvent in the triplet manifold seems to occur faster than triplet decay in acetonitrile, which leads to trapping of the system in either of the calculated T1 minima, with the distribution depending on the amount of excess energy initially available. The removal of excess vibrational energy by the solvent most likely explains the three orders of magnitude slower triplet decay in solution compared to vacuum. Furthermore, in acetonitrile, the 3π5π6* and 3πSπ2* minima are not degenerate (Fig. 7) and therefore, whether population in the T1 state relaxes to the 3π5π6* or to the 3πSπ2* minimum will affect how fast the triplet state can be depopulated. Specifically, population in the 3π5π6* minimum must overcome an energy barrier of 0.36 eV to access the 3πSπ2*/S0 crossing, whereas population in the 3πSπ2* minimum only needs to surmount an energy barrier of 0.28 eV. Thus, excitation with wavelengths shorter than 308 nm seems to populate primarily the 3πSπ2* minimum, whereas excitation at 316 nm seems to populate mostly the 3π5π6* minimum. The latter leads to a slower rate of triplet state decay. It appears that a combination of electronic and vibrational solvent effects leads to a lengthening of the triplet decay lifetime by nearly three orders of magnitude in going from gas phase to acetonitrile.
Conclusions
TRPES and TRAS experiments reveal that the excited-state dynamics of 2-thiouracil can be modulated sensitively depending on the excitation wavelength used. As the excitation wavelength is decreased, high-lying singlet states can be populated, which leads to the population of the lowest-energy 1nπ* state with increasing excess of vibrational energy in both gas and condensed phases. It is proposed that excitation to higher vibrational levels and, in particular, out-of-plane vibrational modes, promote puckering and pyramidalization distortions in 2-thiouracil that are necessary to access ISC pathways. In the gas phase, the excess vibrational energy is used to overcome an energy barrier to access the triplet state, whereas intermolecular energy transfer in solution removes the excess energy before ISC to the triplet state ensues. Specifically, overcoming the energy barrier to access the 1nSπ2*/3πSπ2* intersection seam controls the ISC lifetime to the triplet state, whereas vibrational energy redistribution of the 1nπ*(hot) state is proposed to be the rate-limiting step in the ISC event to the triplet state in solution.We have also shown that triplet state decay to the ground state occurs more rapidly as the excitation energy is increased in both gas and condensed phases. Strikingly, this acceleration in the triplet state decay occurs bimodal in solution, whereas it is continuous in the gas phase. This behavior is explained by the presence of two minima in the potential energy surface of the lowest-energy triplet state, together with the existence of an energy barrier to access the 3πSπ2*/S0 crossing seam. While the calculations show that the energy barrier between both triplet minima does not change appreciably in going from vacuum to acetonitrile and both triplet minima have equal energy in the gas phase, the two minima are non-degenerate in solution. This latter observation seems to explain the decay of the triplet state to the ground state in a bimodal fashion in solution, as the excitation wavelength is decreased, while in the gas phase a continuous acceleration is observed. We note that, while our manuscript was under review, another work was published by Bai and Barbatti60 where the triplet decay of the closely related 2-thiothymine was investigated theoretically using excited-state optimizations and PES scans in the gas phase. Their results fully agree with our gas phase calculations, also finding the two triplet minima and related crossing points.
In conclusion, the experimental and computational results presented in this study show that the accessibility of conical intersections, crossing seams, and energy barriers along the associated singlet and triplet relaxation coordinates can be better understood via a systematic variation of the excitation wavelength in both gas and condensed phases. Specifically, systematic trends among the intersystem crossing lifetimes were revealed with a decrease in excitation wavelength, which can be directly correlated to the topology of the potential energy surfaces, and satisfactorily interpreted by static ab initio calculations that take into consideration solvents effects and that are complementary to the high-level dynamics simulations carried out in vacuum.37
Acknowledgements
This work was supported by the National Science Foundation, grant CHE-1362237 (J. S.-R., A. M., S. U.), and grants CHE-1255084 and CHE-1539808 (B. A., M. P., C. E. C.-H.), and the Austrian Science Fund FWF, grant P25827 (S. M., P. M., L. G.). J. S.-R., A. M., and S. U. would also like to thank Mr T. J. Godfrey for his assistance in the laboratory. Part of the calculations were performed at the Vienna Scientific Cluster (VSC3). We also thank the COST action XLIC (CM1204) for fruitful discussions over the past years.References
- C. E. Crespo-Hernández, B. Cohen, P. M. Hare and B. Kohler, Chem. Rev., 2004, 104, 1977–2019 CrossRef PubMed.
- A. L. Sobolewski and W. Domcke, Europhys. News, 2006, 37, 20–23 CrossRef CAS.
- C. T. Middleton, K. de La Harpe, C. Su, Y. K. Law, C. E. Crespo-Hernández and B. Kohler, Annu. Rev. Phys. Chem., 2009, 60, 217–239 CrossRef CAS PubMed.
- B. Kohler, J. Phys. Chem. Lett., 2010, 1, 2047–2053 CrossRef CAS.
- T. Gustavsson, R. Improta and D. Markovitsi, J. Phys. Chem. Lett., 2010, 1, 2025–2030 CrossRef CAS.
- K. Kleinermanns, D. Nachtigallová and M. S. de Vries, Int. Rev. Phys. Chem., 2013, 32, 308–342 CrossRef CAS.
- M. Barbatti, A. C. Borin and S. Ullrich, Photoinduced Phenomena in Nucleic Acids I, Top. Curr. Chem., Springer, 2015, vol. 355 Search PubMed.
- M. Barbatti, A. C. Borin and S. Ullrich, Photoinduced Processes in Nucleic Acids. I, Top. Curr. Chem., Springer, 2015, vol. 355, pp. 1–32 Search PubMed.
- H. R. Hudock, B. G. Levine, A. L. Thompson, H. Satzger, D. Townsend, N. Gador, S. Ullrich, A. Stolow and T. J. Martínez, J. Phys. Chem., 2007, 111, 8500–8508 CrossRef CAS PubMed.
- S. Ullrich, T. Schultz, M. Z. Zgierski and A. Stolow, Phys. Chem. Chem. Phys., 2004, 6, 2796–2801 RSC.
- C. Z. Bisgaard, H. Satzger, S. Ullrich and A. Stolow, ChemPhysChem, 2009, 10, 101–110 CrossRef CAS PubMed.
- Y. Harada, T. Suzuki, T. Ichimura and Y.-Z. Xu, J. Phys. Chem. B, 2007, 111, 5518–5524 CrossRef CAS PubMed.
- Y. Harada, C. Okabe, T. Kobayashi, T. Suzuki, T. Ichimura, N. Nishi and Y.-Z. Xu, J. Phys. Chem. Lett., 2010, 1, 480–484 CrossRef CAS.
- C. Reichardt and C. E. Crespo-Hernández, J. Phys. Chem. Lett., 2010, 1, 2239–2243 CrossRef CAS.
- H. Kuramochi, T. Kobayashi, T. Suzuka and T. Ichimura, J. Phys. Chem. B, 2010, 114, 8782–8789 CrossRef CAS PubMed.
- C. Reichardt and C. E. Crespo-Hernández, Chem. Commun., 2010, 46, 5963–5965 RSC.
- C. Reichardt, C. Guo and C. E. Crespo-Hernández, J. Phys. Chem. B, 2011, 115, 3263–3270 CrossRef CAS PubMed.
- M. Pollum, S. Jockusch and C. E. Crespo-Hernández, J. Am. Chem. Soc., 2014, 136, 17930–17933 CrossRef CAS PubMed.
- M. Pollum, S. Jockusch and C. E. Crespo-Hernández, Phys. Chem. Chem. Phys., 2015, 17, 27851–27861 RSC.
- M. Pollum, L. Martínez-Fernández and C. E. Crespo-Hernández, in Photoinduced Phenomena in Nucleic Acids I, Top. Curr. Chem., ed. M. Barbatti, A. C. Borin and S. Ullrich, Springer, 2015, vol. 355, pp. 245–327 Search PubMed.
- S. Mai, M. Pollum, L. Martínez-Fernández, N. Dunn, P. Marquetand, I. Corral, C. E. Crespo-Hernández and L. González, Nat. Commun., 2016, 7, 13077 CrossRef CAS PubMed.
- M. Pollum, L. A. Ortiz-Rodríguez, S. Jockusch and C. E. Crespo-Hernández, Photochem. Photobiol., 2016, 92, 286–292 CrossRef CAS PubMed.
- B. Ashwood, S. Jockusch and C. E. Crespo-Hernández, Molecules, 2017, 22, 379 CrossRef PubMed.
- L. Martínez-Fernández, G. Granucci, M. Pollum, C. E. Crespo-Hernández, M. Persico and I. Corral, Chem. – Eur. J., 2017, 23, 2619–2627 CrossRef PubMed.
- P. O’Donovan, C. M. Perrett, X. Zhang, B. Montaner, Y.-Z. Xu, C. A. Harwood, J. M. McGregor, S. L. Walker, F. Hanaoka and P. Karran, Science, 2005, 309, 1871–1874 CrossRef PubMed.
- X. Zhang, G. Jeffs, X. Ren, P. O'Donovan, B. Montaner, C. M. Perrett, P. Karran and Y.-Z. Xu, DNA Repair, 2007, 6, 344–354 CrossRef CAS PubMed.
- P. Karran and N. Attard, Nat. Rev. Cancer, 2008, 8, 24–36 CrossRef CAS PubMed.
- M. Pollum, L. Guan, S. Ahsanuddin, E. Baron, M. Lam and C. E. Crespo-Hernández, J. Invest. Dermatol., 2016, 136, S105 CrossRef.
- O. Reelfs, P. Karran and A. R. Young, Photochem. Photobiol. Sci., 2012, 11, 148–154 CAS.
- G. Trigiante and Y.-Z. Xu, in Photodynamic Therapy: Fundamentals, Applications and Health Outcomes, ed. A. G. Hugo, Nova Science, 2015 Search PubMed.
- M. Pollum and C. E. Crespo-Hernández, J. Chem. Phys., 2014, 140, 071101 CrossRef PubMed.
- V. Vendrell-Criado, J. A. Sáez, V. Ljiaubet-Vallet, M. C. Cuquerella and M. A. Miranda, Photochem. Photobiol. Sci., 2013, 12, 1460–1465 CAS.
- H. Yu, J. A. Sanchez-Rodriguez, M. Pollum, C. E. Crespo-Hernández, S. Mai, P. Marquetand, L. González and S. Ullrich, Phys. Chem. Chem. Phys., 2016, 18, 20168–20176 RSC.
- G. Cui and W. Fang, J. Chem. Phys., 2013, 138, 044315 CrossRef PubMed.
- J. P. Gobbo and A. C. Borin, Comput. Theor. Chem., 2014, 1040–1041, 195–201 CrossRef CAS.
- S. Mai, P. Marquetand and L. González, J. Phys. Chem. A, 2015, 119, 9524–9533 CrossRef CAS PubMed.
- S. Mai, P. Marquetand and L. González, J. Phys. Chem. Lett., 2016, 7, 1978–1983 CrossRef CAS PubMed.
- M. A. El-Sayed, J. Chem. Phys., 1963, 38, 2834–2838 CrossRef CAS.
- N. L. Evans and S. Ullrich, J. Phys. Chem. A, 2010, 114, 11225–11230 CrossRef CAS PubMed.
- H. Yu, N. L. Evans, A. S. Chatterley, G. M. Roberts, V. G. Stavros and S. Ullrich, J. Phys. Chem. A, 2014, 118, 9438–9444 CrossRef CAS PubMed.
- H. Yu, N. L. Evans, V. G. Stavros and S. Ullrich, Phys. Chem. Chem. Phys., 2012, 14, 6266–6272 RSC.
- N. L. Evans, H. Yu, G. M. Roberts, V. G. Stavros and S. Ullrich, Phys. Chem. Chem. Phys., 2012, 14, 10401–10409 RSC.
- T. J. Godfrey, H. Yu and S. Ullrich, J. Chem. Phys., 2014, 141, 044314 CrossRef CAS PubMed.
- A. Khvorostov, L. Lapinski, H. Rostkowska and M. J. Nowak, J. Phys. Chem. A, 2005, 109, 7700–7707 CrossRef CAS PubMed.
- J. H. Eland, Int. J. Mass Spectrom. Ion Phys., 1969, 2, 471–484 CrossRef CAS.
- C. Reichardt, R. A. Vogt and C. E. Crespo-Hernández, J. Chem. Phys., 2009, 131, 224518 CrossRef PubMed.
- C. Reichardt, C. Wen, R. A. Vogt and C. E. Crespo-Hernández, Photochem. Photobiol. Sci., 2013, 12, 1341–1350 CAS.
- J. Finley, P. Å. Malmqvist, B. O. Roos and L. Serrano-Andrés, Chem. Phys. Lett., 1998, 288, 299 CrossRef CAS.
- B. O. Roos, R. Lindh, P. Å. Malmqvist, V. Veryazov and P. O. Widmark, J. Phys. Chem. A, 2004, 108, 2851–2858 CrossRef CAS.
- M. J. Bearpark, M. A. Robb and H. B. Schlegel, Chem. Phys. Lett., 1994, 223, 269 CrossRef CAS.
- L. Serrano-Andrés, M. P. Fülscher and G. Karlström, Int. J. Quantum Chem., 1997, 65, 167–181 CrossRef.
- F. Aquilante, J. Autschbach, R. K. Carlson, L. F. Chibotaru, M. G. Delcey, L. De Vico, I. Fdez. Galván, N. Ferré, L. M. Frutos, L. Gagliardi, M. Garavelli, A. Giussani, C. E. Hoyer, G. Li Manni, H. Lischka, D. Ma, P. Å. Malmqvist, T. Müller, A. Nenov, M. Olivucci, T. B. Pedersen, D. Peng, F. Plasser, B. Pritchard, M. Reiher, I. Rivalta, I. Schapiro, J. Segarra-Martí, M. Stenrup, D. G. Truhlar, L. Ungur, A. Valentini, S. Vancoillie, V. Veryazov, V. P. Vysotskiy, O. Weingart, F. Zapata and R. Lindh, J. Comput. Chem., 2016, 37, 506–541 CrossRef CAS PubMed.
- C. Puzzarini, M. Biczysko, V. Barone, I. Peña, C. Cabezas and J. L. Alonso, Phys. Chem. Chem. Phys., 2013, 15, 16965–16975 RSC.
- M. K. Shukla and J. Leszczynski, J. Phys. Chem. A, 2004, 108, 10367–10375 CrossRef CAS.
- A. R. Katritzky, M. Szafran and G. Pfister-Guillouzo, J. Chem. Soc., Perkin Trans. 2, 1990, 871–876 RSC.
- M. Ruckenbauer, S. Mai, P. Marquetand and L. González, J. Chem. Phys., 2016, 144, 074303 CrossRef PubMed.
- F. Laermer, T. Elsaesser and W. Kaiser, Chem. Phys. Lett., 1989, 156, 381 CrossRef CAS.
- When using a pump wavelength of 316 nm, a higher concentration of 2-thiouracil was used in order to improve the signal to noise ratio because the ground-state molar absorptivity of 2-thiouracil is much smaller at 316 nm than at 268 or 290 nm. This is likely the reason for the observation of triplet self-quenching at 316 nm, but not at the other two excitation wavelengths.
- K. Taras-Goślińska, G. Burdziński and G. Wenska, J. Photochem. Photobiol., A, 2014, 275, 89 CrossRef.
- S. Bai and M. Barbatti, Phys. Chem. Chem. Phys., 2017, 19, 12674–12682 RSC.
- J. P. Zobel, J. J. Nogueira and L. González, Chem. Sci., 2017, 8, 1482–1499 RSC.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c7cp02258a |
| ‡ These authors contributed equally to this work. |
| This journal is © the Owner Societies 2017 |