XUV-induced reactions in benzene on sub-10 fs timescale: nonadiabatic relaxation and proton migration
Abstract
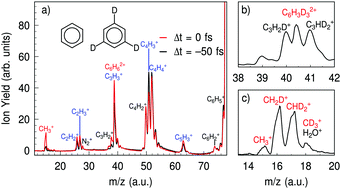
Unraveling ultrafast dynamical processes in highly excited molecular species has an impact on our understanding of chemical processes such as combustion or the chemical composition of molecular clouds in the universe. In this article we use short (<7 fs) XUV pulses to produce excited cationic states of benzene molecules and probe their dynamics using few-cycle VIS/NIR laser pulses. The excited states produced by the XUV pulses lie in an especially complex spectral region where multi-electronic effects play a dominant role. We show that very fast τ ≈ 20 fs nonadiabatic processes dominate the relaxation of these states, in agreement with the timescale expected for most excited cationic states in benzene. In the CH3+ fragmentation channel of the doubly ionized benzene cation we identify pathways that involve structural rearrangement and proton migration to a specific carbon atom. Further, we observe non-trivial transient behavior in this fragment channel, which can be interpreted either in terms of propagation of the nuclear wavepacket in the initially excited electronic state of the cation or as a two-step electronic relaxation via an intermediate state.
- This article is part of the themed collection: XUV/X-ray light and fast ions for ultrafast chemistry


 Please wait while we load your content...
Please wait while we load your content...