Electronic structure and time-dependent description of rotational predissociation of LiH
Abstract
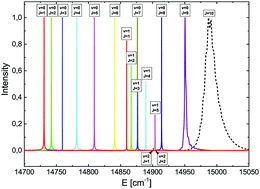
The adiabatic potential energy curves of the 1Σ+ and 1Π states of the LiH molecule were calculated. They correlate asymptotically to atomic states, such as 2s + 1s, 2p + 1s, 3s + 1s, 3p + 1s, 3d + 1s, 4s + 1s, 4p + 1s and 4d + 1s. A very good agreement was found between our calculated spectroscopic parameters and the experimental ones. The dynamics of the rotational predissociation process of the 11Π state were studied by solving the time-dependent Schrödinger equation. The classical experiment of Velasco [Can. J. Phys., 1957, 35, 1204] on dissociation in the 11Π state is explained for the first time in detail.
- This article is part of the themed collection: XUV/X-ray light and fast ions for ultrafast chemistry


 Please wait while we load your content...
Please wait while we load your content...