Spectral dependence of photoemission in multiphoton ionization of NO2 by femtosecond pulses in the 375–430 nm range†
Abstract
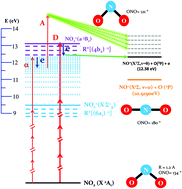
We investigate the multiphoton ionization of NO2 using tunable (430–375 nm) femtosecond pulses and photoelectron–photoion coincidence momentum spectroscopy. In order to understand the complex electronic and nuclear photodynamics at play following absorption of three to five photons, we also report extended photoionization calculations using correlated targets and coupled channels. Exploring the multiphoton dissociative ionization (MPDI) and multiphoton ionization (MPI) processes over such a broad energy range enables us to lend further support to our work carried out around 400 nm of a femtosecond laser [S. Marggi Poullain et al., J. Phys. B: At., Mol. Opt. Phys., 2014, 47, 124024]. Two excitation energy regions are identified and discussed in terms of the proposed reaction pathways, highlighting the significant role of Rydberg states, such as the [R*(6a1)−1, 3pσ] Rydberg state, in the NO2 multiphoton excitation and photoionization. These new results support our previous assumption that different bent and linear geometries of the NO2+(X1Σg) ionic state contribute to the MPDI and MPI, consistent with the reported calculations which reveal an important vibronic coupling characterizing the photoemission. Remarkably, the strong anisotropy of the recoil frame photoelectron angular distribution (RFPAD) previously observed at 400 nm appears as a fingerprint across the whole explored photon energy range.
- This article is part of the themed collection: XUV/X-ray light and fast ions for ultrafast chemistry


 Please wait while we load your content...
Please wait while we load your content...