Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Role of electronic correlations in photoionization of NO2 in the vicinity of the 2A1/2B2 conical intersection
Danilo S.
Brambila
 *ab,
Alex G.
Harvey
a,
Karel
Houfek
c,
Zdeněk
Mašín
*ab,
Alex G.
Harvey
a,
Karel
Houfek
c,
Zdeněk
Mašín
 a and
Olga
Smirnova
*ad
a and
Olga
Smirnova
*ad
aMax-Born-Institute, Max-Born-Strasse 2A, D-12489 Berlin, Germany. E-mail: Olga.Smirnova@mbi-berlin.de
bFritz-Haber-Institut der Max-Planck-Gesellschaft, Faradayweg 4-6, D-14195 Berlin, Germany. E-mail: brambila@fhi-berlin.mpg.de
cInstitute of Theoretical Physics, Faculty of Mathematics and Physics, Charles University Prague, V Holešovičkách ch 2, 180 00 Praha 8, Czech Republic
dInstitut für Theoretische Physik, Nichtlineare Optik und Quantenelektronik, Technische Universität Berlin, 10623 Berlin, Germany
First published on 17th May 2017
Abstract
We present the first ab initio multi-channel photoionization calculations for NO2 in the vicinity of the 2A1/2B2 conical intersection, for a range of nuclear geometries, using our newly developed set of tools based on the ab initio multichannel R-matrix method. Electronic correlation is included in both the neutral and the scattering states of the molecule via configuration interaction. Configuration mixing is especially important around conical intersections and avoided crossings, both pertinent for NO2, and manifests itself via significant variations in photoelectron angular distributions. The method allows for a balanced and accurate description of the photoionization/photorecombination for a number of different ionic channels in a wide range of photoelectron energies up to 100 eV. Proper account of electron correlations is crucial for interpreting time-resolved signals in photoelectron spectroscopy and high harmonic generation (HHG) from polyatomic molecules.
1 Introduction
Understanding molecular photochemical reactions is a challenging task due to both the large number of excited states that usually participate in the reaction and the various intra-molecular radiationless processes, which redistribute the charge and vibrational energy of the molecule. These include, e.g., internal conversion, isomerization, and proton or electron transfer.1–3 Greater insight into these photochemical reactions, and the corresponding underlying dynamical processes, can be obtained by performing experiments in the time domain. Typically, this involves pump–probe experiments where: (i) a pump laser pulse excites the molecule, creating a wavepacket consisting of a coherent superposition of the molecular eigenstates; (ii) the wavepacket propagates in the energetically accessible regions of the reaction coordinates; (iii) and finally, the wavepacket is probed by the most suitable technique (e.g. laser induced fluorescence,4 resonant multiphoton ionization,5,6 photoionization,7 high harmonic generation8–10 and transient absorption11,12). Time-resolved information on the photochemical reaction is obtained by using a variable delay between the pump and the probe.Interpreting the information recorded in the pump–probe signal is, however, challenging. In particular, the dynamics induced by the pump step is often entangled with the complexity of the final state, or a superposition of such states, accessed by the probe. Here, we focus on how this challenge manifests itself when photoelectron spectroscopy or high harmonic generation is used as a probe step.
Time-resolved photoelectron spectroscopy (TRPES) is a powerful and wide-spread technique for investigating photochemical reactions.13 There are several reasons for using photoelectron spectroscopy as a probe in time-resolved experiments. First, XUV light can be used to photoionize valence electrons, thus providing valuable insight into the chemically active molecular orbitals of the target. Second, photoionization is always an allowed process, so it can be used to probe, in principle, all the reaction coordinates. Third, low intensity XUV radiation can be treated using first-order perturbation theory, thus greatly simplifying the theoretical treatment of the ionization process.
Moreover, new FEL facilities and HHG sources are now able to deliver broadband XUV radiation with ∼10 fs duration, giving access to the fastest molecular processes with unprecedented temporal resolution.7,14 These advances have stimulated a growing number of experimental and theoretical efforts for investigating several aspects of molecular dynamics, e.g., to map the electronic character of molecules along the reaction path,15–17 to shed light on the deactivation pathways of complex molecules,18–20 and most relevant for this work, to elucidate the non-adiabatic dynamics in polyatomic molecules.21–26
High harmonic generation (HHG) provides complementary information to photoelectron spectroscopy. Indeed, the radiative photorecombination step in HHG, which is responsible for the emission of a high-frequency photon, is an inverse of the photoionization step in photo-electron spectroscopy. Notably, when several final states of the ion participate in photoionization, the photoelectron spectra contain incoherent superposition of the contributions correlated to these final ionic states. In contrast, high harmonic generation encodes the interference of these ionic channels and hence the relative phases between them, which determine the dynamics of the hole created by ionization and can be reconstructed from the measurements.27–33
The interferometric property of HHG places particular premium on a balanced and accurate description of the photorecombination step from the number of different participating ionic channels, therefore demanding a high-level modelling of correlation and polarization. Additionally, for complex molecules the use of longer-wavelength (mid-infrared) pulses of the driving field is necessary.34,35 This in turn leads to larger energies of the recombining electron. Therefore, accurate theoretical modelling of HHG requires the extension of the energy region available in photoionization calculations, which is a challenging task for current state-of-art high-quality multichannel calculations. The data presented in this work satisfy these demanding requirements and open the way towards the calculations of HHG from NO2 including the effects of nuclear motion.
To describe the photoionization step, the existing state-of-the-art wavefunction-based theoretical studies of TRPES21,36 use a high-quality configuration interaction (CI) description of the bound molecular states, but a single Slater determinant description of the residual ionic states. This approach neglects the electronic correlation in the ions, an assumption that is particularly crude for treating highly excited ionic states, or the region of the reaction coordinates where non-adiabatic dynamics may affect the ion. We address this limitation here using the multichannel R-matrix method. The calculations are performed using the UKRmol + package,37–39 which allows us to describe the electronic correlation in several neutral and ionic molecular states via configuration interaction. In this paper, we concentrate exclusively on the photoionization process in TRPES. The coupling of the photoionization calculations performed here with nuclear dynamics for TRPES or time-resolved high harmonic spectroscopy is the subject of a future work.
In this work, we extend our previous results for the photoionization of NO2 in the equilibrium geometry,40 and demonstrate the first application of the R-matrix method for the photoionization of polyatomic molecules for several nuclear geometries. Here, we restrict our analysis to photoionization from the ground and the first excited neutral states of NO2, leaving the residual ion in the lowest energy singlet and triplet ionic states for an asymmetric stretching varying from 0 to 0.2 Å and bending angles from 80° to 160°. We are interested in studying photoionization transitions close to the conical intersection between the ground and the first excited neutral states of NO2,21 which occurs at a bending angle of ≈107°. Previous quantum chemical calculations41 have shown the existence of an avoided crossing between the two lowest energy singlet ionic states of NO2 also at ≈107°. Consequently, a precise evaluation of the photoionization matrix elements for such a transition requires a careful description of electronic correlation for both neutral and the singlet ionic states.
This paper is organized as follows: in Section 2, we briefly describe the principles of the R-matrix method. In Section 3, we present the details of the calculations and in Section 4, we report the orientationally averaged results and the photoelectron angular distributions (PADs) for the photoionization of the NO2 molecule in a range of nuclear geometries. Finally, in Section 5, we present the conclusions and future directions of this work.
2 Photoionization calculations using the R-matrix method
The molecular-frame photoelectron angular distribution for photoionization from the ΦNi bound state and leaving the ion in the ϕN−1f state is given by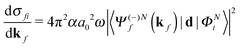 | (1) |
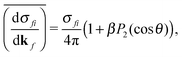 | (2) |
The R-matrix method divides the configurational space into an inner (r ≤ a) and an outer (r > a) region. The R-matrix radius, a, is chosen in such a way that only the continuum electron reaches the R-matrix boundary. In the inner region, both the continuum and the bound-state wavefunctions are given in terms of the basis functions, ψNk, as
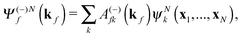 | (3) |
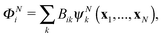 | (4) |
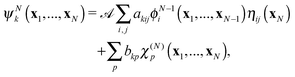 | (5) |
![[scr A, script letter A]](https://www.rsc.org/images/entities/char_e520.gif) is the antisymmetrisation operator, bkp and akij are coefficients determined by diagonalization of the Hamiltonian. In the second summation, χ(N)p are the so-called L2 configurations, which improve the description of electron correlation, polarization and help in converging the partial wave expansion by allowing the continuum electron to enter high angular momentum states close to the nuclei. They are formed by allowing the continuum electron to occupy target molecular orbitals. The reason they need to be explicitly added is that the one electron continuum functions are orthogonalized to the target molecular orbitals. Restricting the continuum electron to the continuum orbitals would neglect an important part of the Hilbert space.
is the antisymmetrisation operator, bkp and akij are coefficients determined by diagonalization of the Hamiltonian. In the second summation, χ(N)p are the so-called L2 configurations, which improve the description of electron correlation, polarization and help in converging the partial wave expansion by allowing the continuum electron to enter high angular momentum states close to the nuclei. They are formed by allowing the continuum electron to occupy target molecular orbitals. The reason they need to be explicitly added is that the one electron continuum functions are orthogonalized to the target molecular orbitals. Restricting the continuum electron to the continuum orbitals would neglect an important part of the Hilbert space.
Following the assumption that only the continuum electron reaches the R-matrix boundary, the outer region solutions are found by matching with known asymptotic solutions. The coefficients of the continuum and the bound state wavefunctions (A(−)kf(kf) and Bik, respectively) are then found after matching the solutions of the inner and the outer region at the R-matrix boundary (see ref. 39 for further details).
3 Calculations
As illustrated in Fig. 1, NO2 has three vibrational modes: symmetric stretch, scissors and asymmetric stretch. The latter is defined as the simultaneous shortening of one of the N–O bond lengths by ra/2, and the stretching of the other N–O bond length by ra/2. The ground state equilibrium geometry has C2v symmetry with a bond distance of rs ≈ 1.25 Å and an O–N–O angle of γ ≈ 133°. In this paper, the molecule is fixed in the zx plane, with the z-axis coinciding with the molecular axis (see Fig. 1). We consider here variations of the asymmetric stretch (ra) and bending angle (γ). For this reason, the calculations are performed in the Cs point symmetry group, since a non-zero asymmetric stretch breaks the symmetry of the molecule with respect to reflection in the zy plane. Consequently, the ground and first excited neutral states of NO2, which belong to the A1 and B1 irreducible representations in C2v (only for ra = 0), respectively, are both mapped into A′ symmetry in Cs.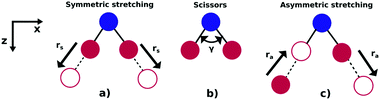 | ||
| Fig. 1 Vibrational modes of the NO2 molecule: (a) symmetric stretch, (b) scissors and (c) asymmetric stretching. | ||
3.1 Molecular orbitals and target models
In Cs symmetry, the ground electronic configuration of NO2 at the equilibrium geometry is given by| (1 − 3a′)6(4 − 7a′)8(1a′′)2(8a′)2(2a′′)2(9a′)2(10a′)1 |
In our calculations, we generate using MOLPRO43 the molecular orbitals on a grid of geometries using a state averaged MCSCF procedure using the 6-311G** atomic basis.44 Hartree–Fock orbitals at the equilibrium geometry were used as an initial guess for the state averaged MCSCF procedure. We included in the state averaging the (1–2)1A′, (1–2)1A′′, (1–2)3A′, (1–2)3A′′ ionic and the (1)2A′ and (2)2A′ neutral states. Both neutral states had a weight of 30% in the averaging. Following our previous work on the photoionization of NO2 at the equilibrium geometry,40 we defined an active space consisting of the 6–10a′ and 1–3a′′ orbitals, and tested its two different variants: model-1, which includes single excitations to the 11–14a′ orbitals, and model-2 that extends the single excitations up to the 11–15a′, 4a′′ orbitals (see Table 1). Note that in our approach, the target configuration state functions (CSFs) are coupled to the continuum electron via the close-coupling equation, see eqn (5). Consequently, it is important to use an optimal number of target CSFs, in order to keep the size of the N-electron Hamiltonian manageable and also to obtain an accurate description of the continuum and bound wavefunctions.
| Target models | Active space | CSFs |
|---|---|---|
| Model-1 | (1–5a′)10(6–10a′, 1–3a′′)12 | 3219 |
| (1–5a′)10(6–10a′, 1–3a′′)11(11–14a′)1 | ||
| Model-2 | (1–5a′)10(6–10a′, 1–3a′′)12 | |
| (1–5a′)10(6–10a′, 1–3a′′)11(11–15a′, 4a′′)1 | 4731 | |
Little difference was observed in the potential energy surfaces generated from the two different target models. In Fig. 2, we show the potential energy curves obtained from model-1 (solid lines) for ra = 0 Å and 80° < γ < 160°. Red, orange, blue and green plots corresponds to the curves from the (1)1A′, (1)3A′ ionic and the (1)2A′, (2)2A′ neutral states, respectively. The dots correspond to the calculations from ref. 41 for the ionic, and from ref. 42 for the neutral states. In general, we observe a good agreement between the potential energy surfaces obtained from model-1 and the results from ref. 41 and 42.
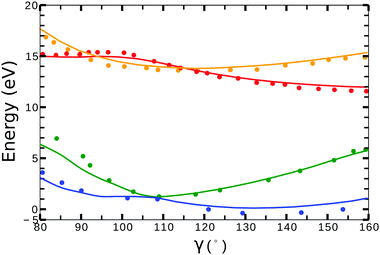 | ||
| Fig. 2 Potential energy curves (ra = 0) for the (1)2A′ (blue), (2)2A′ (green) neutral and (1)3A′ (orange), (1)1A′ (red) ionic states of NO2. Solid lines correspond to the calculations using the target orbitals from model-1 (see Table 1). Dots correspond to the calculations from ref. 41 for the cationic, and from ref. 42 for the neutral states. | ||
3.2 Inner and outer regions
The continuum orbitals were generated using Gaussian-type orbitals (GTOs), with angular momentum up to l = 6 and optimized to represent the continuum up to 90 eV. The exponents of the continuum GTOs centered at the center of mass of the molecule are listed in Table 2. The molecular integrals in the inner region were computed in quadruple precision. This allowed us to avoid numerical linear dependency problems and retain all the continuum functions in the basis. For each geometry, the 16 lowest energy virtual orbitals were included in the calculations for improving the description of polarization in the inner region. Convergence for all models, with respect to the number of states included in the close coupling expansion, was achieved for calculations with at least 80 target states.| Angular momentum | Gaussian exponent |
|---|---|
| l = 0 | 33.559323, 2.576968, 0.276187, 0.184632, 0.126330, 0.086941, 0.059603, 0.040429, 0.026977, 0.017594, 0.011082 |
| l = 1 | 1.546842, 0.367220, 0.254952, 0.182860, 0.133060, 0.097244, 0.070868, 0.051199, 0.036466, 0.025435, 0.017157 |
| l = 2 | 0.437039, 0.303223, 0.217211, 0.158560, 0.116878, 0.086332, 0.063474, 0.046155, 0.032943, 0.022774 |
| l = 3 | 0.409883, 0.291455, 0.213760, 0.159587, 0.120199, 0.090678, 0.068084, 0.050566, 0.036876, 0.026055 |
| l = 4 | 0.340244, 0.243185, 0.179271, 0.134479, 0.101646, 0.076790, 0.057555, 0.042443, 0.030365 |
| l = 5 | 0.225709, 0.167874, 0.128505, 0.099316, 0.076719, 0.058780, 0.044303, 0.032392 |
| l = 6 | 0.118188, 0.085985, 0.062824, 0.045463, 0.032349, 0.022480, 0.015073 |
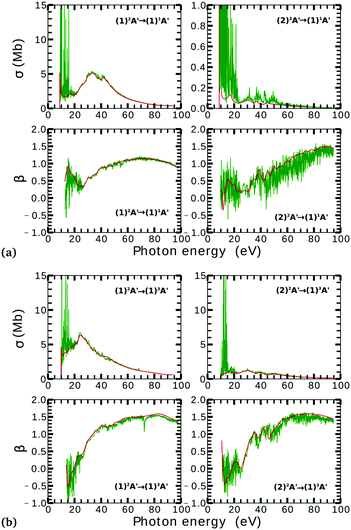
Due to computational limitations, we only performed convergence tests at the photoionization level for a few critical molecular geometries at the extremes of the angular grid. As indicated in Fig. 3 and 4, there is a good agreement on the asymmetry parameter and partial cross-sections between calculations using model-1 and model-2. Since model-1 is computationally cheaper than model-2, the former was chosen for the photoionization calculations over the whole grid of nuclear geometries.
We used the Perl scripts45 to prepare the input files and to drive and monitor the complex sequence of R-matrix programs which have to be executed to complete the calculation for multiple geometries. The scripts were originally developed for the calculations of electron–molecule collisions and subsequently adapted to enable photoionization and execution on large computer clusters. The structure of the scripts comprises definitions, for each program, of the input generation, program execution and output analysis, followed by a specification of the calling sequence of all programs. This system is therefore very flexible with respect to the inclusion of new programs in the suite and is very helpful in organizing large amounts of output data.
4 Results
4.1 Orientationally averaged results
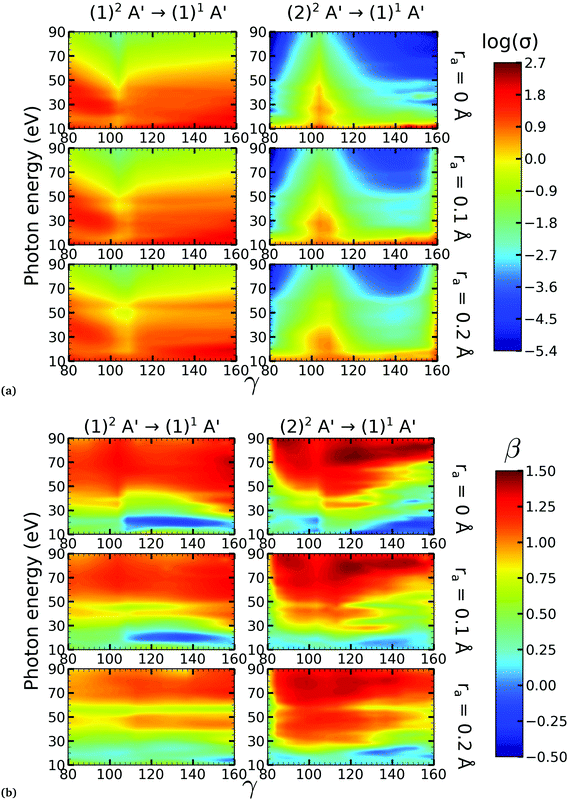
There is a strong correlation between the partial photoionization cross-sections and the dominant electronic configurations of the neutral (initial) and cationic (final) states. Changes in molecular geometry can lead to changes in the dominant electronic configurations, thus leading to variations in the partial photoionization cross-section. This is observed in Fig. 5(a), where far from the conical intersection, the (1)1A′ ionic and (1)2A′ and (2)2A′ neutral states have the following electronic configuration:
˙ the (1)1A′ ionic state has a leading configuration of …(9a′)0(10a′)2 for γ < 100° and …(9a′)2(10a′)0 for γ > 115°. The change in the electronic configuration of this state occurs at γ ≈ 107°, due to the avoided crossing between the (1)1A′ and (2)1A′ states.
˙ the (1)2A′ neutral state has a leading configuration of …(9a′)1(10a′)2 for γ < 100° and …(9a′)2(10a′)1 for γ >115°.
˙ the (2)2A′ neutral state has a leading configuration of …(9a′)2(10a′)1 for γ < 100° and …(9a′)1(10a′)2 for γ >115°.
Note that far from the conical intersection, the leading electronic configuration of the (1)1A′ ionic state is always a 1h state with respect to the (1)2A′ neutral state. Consequently, we observe a large magnitude of the partial photoionization cross-section for the (1)2A′ → (1)1A′ photoionization transition for γ < 100° and γ > 115° (see the left column of Fig. 5(a)). On the other hand, far from the conical intersection, the leading electronic configuration of the (1)1A′ ion is always a satellite state (2h–1p) with respect to the (2)2A′ neutral. The photoionization transitions are then mediated through at least one non-dominant electronic configuration, thus leading to a low magnitude of the partial photoionization cross-section for the (2)2A′ → (1)1A′ transition (see the right column of Fig. 5(a)).
Close to the conical intersection, the neutral states are strongly coupled, thus, we observe that the partial photoionization cross-section decreases for the (1)2A′ → (1)1A′ photoionization transition, and increases for the (2)2A′ → (1)1A′ photoionization transition. We note that the avoided crossing between the (1)2A′ and the (2)1A′ ionic states at γ ≈ 107° also leads to a strong coupling between these states. Consequently, photoionization calculations that do not describe correctly the effect of electronic correlation in the (1)1A′ state fail to accurately evaluate the (1)2A′ → (1)1A′ and (2)2A′ → (1)1A′ photoionization transitions at γ ≈ 108°.
In Fig. 5(b) we plot the asymmetry parameter for photoionization from both neutral states leaving the ion in the (1)1A′ state. At photon energies below 50 eV, we notice a pronounced change of the asymmetry parameter as γ passes by the conical intersection. The increased sensitivity at low energies goes hand in hand with the variation of the photoionization cross-sections at low energies. On the other hand, at photon energies above 50 eV there is almost no signature of the change in electronic configurations of the neutral or the ionic states for 80° < γ < 160°.
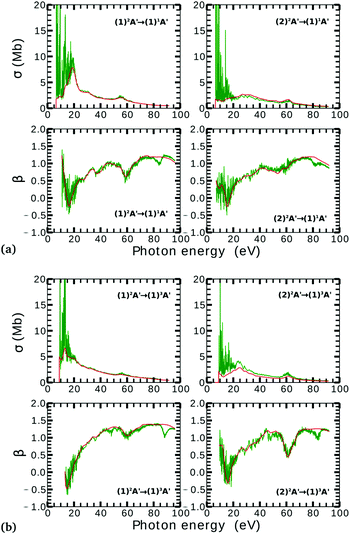
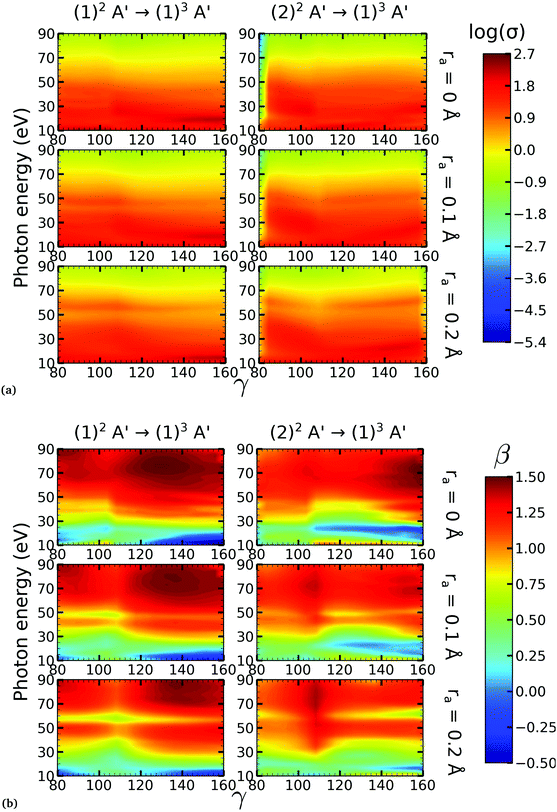
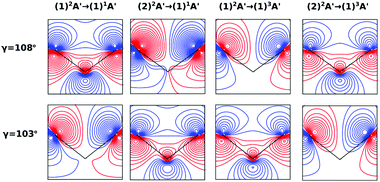
On the other hand, the asymmetry parameter for the (1)2A′ → (1)3A′ and (2)2A′ → (1)3A′ transitions shown in Fig. 6(b) exhibits a sudden change in amplitude when crossing the conical intersection at low photon energies. This indicates that even though the dipole transition strength is approximately constant for all geometries considered, the angular distribution of the ejected electrons varies considerably as the molecule crosses the conical intersection. This is confirmed in Fig. 7, where we plot the Dyson orbitals in the zx plane for the (1)2A′ → (1)1A′ and (2)2A′ → (1)1A′ photoionization transitions in the vicinity of the conical intersection. We can see that as the system goes through the conical intersection, the Dyson orbitals for the (1)2A′ → (1)1A′ and (2)2A′ → (1)1A′ transitions are swapped. The result is the appearance and disappearance of the nodal plane, respectively, along the molecular axis in the two Dyson orbitals as γ varies from 108° to 103°. This shows that even for a non-oriented ensemble of molecules, one could use the asymmetry parameter to identify changes in the electronic configuration of the neutral states.
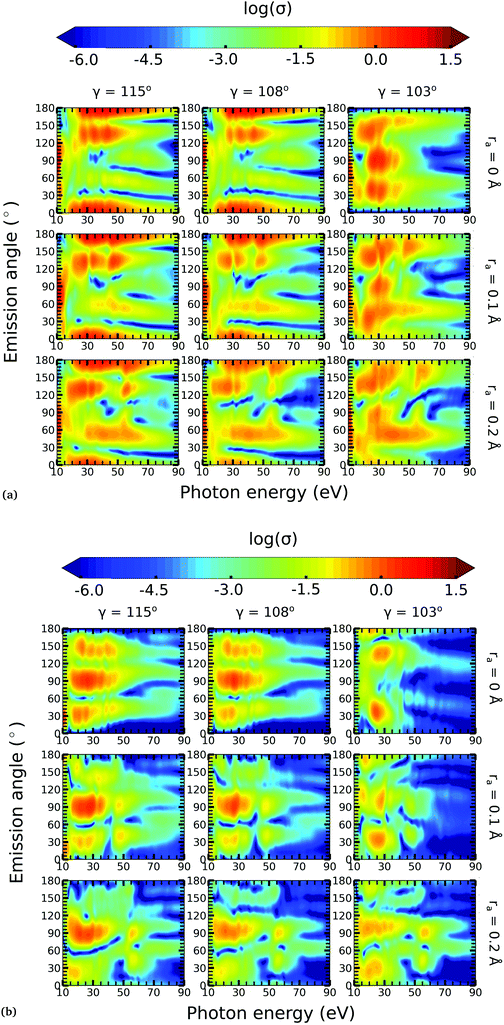
4.2 Photoelectron angular distributions
In this work, we calculated the PADs for parallel and perpendicular alignments for transitions from the (1)2A′ and (2)2A′ neutral states to the (1)1A′ and (1)3A′ ionic states in the range of molecular geometries of 80° ≤ γ ≤ 160°, 0 Å ≤ ra ≤ 0.4 Å. However, we will restrict ourselves to the discussion of the PADs for the (1)2A′ → (1)1A′ photoionization transition near the conical intersection and only examine emission in the xz plane, which is the preferred plane for photoemission8 in NO2.In Fig. 8, we show the PADs for the (1)2A′ → (1)1A′ transition for parallel and perpendicular alignments at bending angles of 115°, 108°, and 103° and asymmetric stretchings of 0 Å, 0.1 Å and 0.2 Å. The emission angle is measured from the molecular axis in the zx plane. At ra = 0 Å, we observe a node along the molecular axis in the PADs for γ < 107° in the case of parallel alignment (Fig. 8(a)) and for γ > 107° in the case of perpendicular alignment (Fig. 8(b)). The origin of this node can be explained by analyzing the photoionization transition in the C2v point group which, at ra = 0, includes the invariance of the molecule upon reflection in the zy plane. In C2v, the (1)2A′ neutral state maps into the (1)2A1 state for γ > 107°, and into the (1)2B1 state for γ < 107°. Since, in the case of parallel alignment, the dipole operator has A1 symmetry, the scattering states must necessarily have A1 symmetry for γ > 107° and B1 symmetry for γ < 107°. Consequently, since the singlet state (1)1A′ maps into A1 in C2v, the continuum electron has to belong to A1 symmetry for γ > 107° and to B1 symmetry for γ < 107°. As the states with B1 symmetry are antisymmetric under reflection in the zy plane, the continuum electron exhibits a node at the molecular axis for γ < 107° (see Fig. 7 and 8(a)). A similar analysis shows that the reverse occurs for perpendicular alignment, i.e., the node at the molecular axis occurs for γ > 107° (see Fig. 8(b)).
The PADs also can be used to identify the main partial wave channels that contribute to the photoelectron signal. Taking again as an example the PAD for parallel alignment and ra = 0, the continuum electron necessarily belongs to B1 symmetry for γ < 107° (see the PADs corresponding to γ < 107° and ra = 0 in Fig. 8(a)). In B1 symmetry, the partial waves can have any value of l and m must be odd. However, an examination of the Legendre polynomials for this set of quantum numbers demonstrates that only partial waves with an odd l value have a maximum at an angle of 90° with respect to the molecular axis. Consequently, we conclude that the partial waves with l = 3 and l = 5 dominate the PADs for photon energies from 30 to 50 eV.
5 Conclusions
We performed NO2 photoionization calculations for a range of geometries close to the conical intersection between the (1)2A′ and (2)2A′ neutral states. We analyzed partial cross-sections, asymmetry parameters, Dyson orbitals and PADs for photoionization leaving the ion in the (1)1A′ and (1)3A′ states. At ra = 0 Å, we identify a peak in the partial cross-section for photoionization from the (2)2A′ state leaving the ion in the (1)1A′ state, which appears due to the conical intersection in the neutral and the avoided crossing between the (1)1A′ and (2)1A′ ionic states at 102° < γ < 107°. Away from this region the signal is low. This is due to the character of the ionic state changing from a satellite to a main line state when passing through the conical intersection (γ ≈ 107°), and then back to a satellite state when passing through the avoided crossing (γ ≈ 102°). The opposite happens with ionization from the (1)2A′ state with a dip showing up at 102° < γ < 107°. The cross-section for photoionization leaving the ion in the (1)3A′ state is relatively homogeneous throughout the range of geometries investigated since this ionic state is always a 1h state with respect to the initial neutral state. In both cases, the asymmetry parameter exhibited a clear signature of the molecular orbitals from which the photoelectron was ejected, i.e., a significant change in magnitude as the molecule goes through the conical intersection, especially at energies below 40 eV.To the best of our knowledge, we presented in this paper the first photoionization calculations over a large grid of nuclear geometries using robust CI methods for describing both the neutral and the ionic states. We find that the effects of configuration-interaction are especially important to describe accurately photoionization leaving the ion in the (1)1A′ state (see Fig. 5(a)) and should be taken into account when interpreting the time-resolved photoelectron spectra, which map the dynamics taking place on multiple potential energy surfaces of the molecule and their interplay via the conical intersection,21 since the range of geometries for which the configuration mixing is important is relatively large.
Our approach allows us to perform calculations of TRPES using broad-band XUV probe laser pulses, which leave the ion in highly excited states after ionization, thus providing rich information regarding the electron dynamics of polyatomic molecules in non-adiabatic regions of the reaction coordinates. In addition, we highlight that our results are also relevant for high harmonic spectroscopy,8 since the recombination step in HHG is strongly linked to the one-photon ionization described here (see ref. 33 and 46–48).
Acknowledgements
The authors gratefully acknowledge the support of their collaboration through European Cooperation in Science and Technology (COST), program CM1204 XLIC. Z. M. and O. S. acknowledge the support of the DFG grant 292/5-1. K. H. acknowledges the support by the Czech Grant Agency grant GACR 16-17230S. Open Access funding provided by the Max Planck Society.References
- M. Bixon and J. Jortner, J. Chem. Phys., 1968, 48, 715–726 CrossRef CAS.
- J. Jortner, S. A. Rice and R. M. Hochstrasser, Adv. Photochem., John Wiley & Sons, Inc., 2007, pp. 149–309 Search PubMed.
- W. Domcke and G. Stock, Adv. Chem. Phys., John Wiley & Sons, Inc., 2007, pp. 1–169 Search PubMed.
- J. L. Kinsey, Annu. Rev. Phys. Chem., 1977, 28, 349–372 CrossRef CAS.
- L. Armstrong, B. L. Beers and S. Feneuille, Phys. Rev. A: At., Mol., Opt. Phys., 1975, 12, 1903–1910 CrossRef.
- S. N. Dixit and P. Lambropoulos, Phys. Rev. A: At., Mol., Opt. Phys., 1983, 27, 861–874 CrossRef CAS.
- J. Ullrich, A. Rudenko and R. Moshammer, Annu. Rev. Phys. Chem., 2012, 63, 635–660 CrossRef CAS PubMed.
- H. J. Wörner, J. B. Bertrand, B. Fabre, J. Higuet, H. Ruf, A. Dubrouil, S. Patchkovskii, M. Spanner, Y. Mairesse, V. Blanchet, E. Mével, E. Constant, P. B. Corkum and D. M. Villeneuve, Science, 2011, 334, 208–212 CrossRef PubMed.
- H. Ruf, C. Handschin, A. Ferré, N. Thiré, J. B. Bertrand, L. Bonnet, R. Cireasa, E. Constant, P. B. Corkum, D. Descamps, B. Fabre, P. Larregaray, E. Mével, S. Petit, B. Pons, D. Staedter, H. J. Wörner, D. M. Villeneuve, Y. Mairesse, P. Halvick and V. Blanchet, J. Chem. Phys., 2012, 137, 224303 CrossRef CAS PubMed.
- A. Ferrè, H. Soifer, O. Pedatzur, C. Bourassin-Bouchet, B. Bruner, R. Canonge, F. Catoire, D. Descamps, B. Fabre, E. M'ievel, S. Petit, N. Dudovich and Y. Mairesse, Phys. Rev. Lett., 2016, 116, 053002 CrossRef PubMed.
- R. Berera, R. van Grondelle and J. T. M. Kennis, Photosynth. Res, 2009, 101, 105–118 CrossRef CAS PubMed.
- E. Goulielmakis, Z.-H. Loh, A. Wirth, R. Santra, N. Rohringer, V. S. Yakovlev, S. Zherebtsov, T. Pfeifer, A. M. Azzeer and M. F. Kling, et al. , Nature, 2010, 466, 739–743 CrossRef CAS PubMed.
- A. Stolow, A. E. Bragg and D. M. Neumark, Chem. Rev., 2004, 104, 1719–1758 CrossRef CAS PubMed.
- K. L. Reid, Annu. Rev. Phys. Chem., 2003, 54, 397–424 CrossRef CAS PubMed.
- S. Ullrich, T. Schultz, M. Z. Zgierski and A. Stolow, Phys. Chem. Chem. Phys., 2004, 6, 2796–2801 RSC.
- A. Toniolo, A. L. Thompson and T. J. Martínez, Chem. Phys., 2004, 304, 133–145 CrossRef CAS.
- Y. Liu, B. Tang, H. Shen, S. Zhang and B. Zhang, Opt. Express, 2010, 18, 5791–5801 CrossRef CAS PubMed.
- J. Wan, J. Meller, M. Hada, M. Ehara and H. Nakatsuji, J. Chem. Phys., 2000, 113, 7853–7866 CrossRef CAS.
- E. V. Gromov, A. B. Trofimov, N. M. Vitkovskaya, H. Köppel, J. Schirmer, H.-D. Meyer and L. S. Cederbaum, J. Chem. Phys., 2004, 121, 4585–4598 CrossRef CAS PubMed.
- T. Fuji, Y.-I. Suzuki, T. Horio, T. Suzuki, R. Mitrić, U. Werner and V. Bonačić-Koutecký, J. Chem. Phys., 2010, 133, 234303 CrossRef PubMed.
- Y. Arasaki, K. Takatsuka, K. Wang and V. McKoy, J. Chem. Phys., 2010, 132, 124307 CrossRef PubMed.
- S. P. Neville, Y. Wang, A. E. Boguslavskiy, A. Stolow and M. S. Schuurman, J. Chem. Phys., 2016, 144, 014305 CrossRef PubMed.
- R. Schneider and W. Domcke, Chem. Phys. Lett., 1988, 150, 235–242 CrossRef CAS.
- M. Thoss, W. H. Miller and G. Stock, J. Chem. Phys., 2000, 112, 10282–10292 CrossRef CAS.
- U. Werner, R. Mitrić and V. Bonačić-Koutecký, J. Chem. Phys., 2010, 132, 174301 CrossRef PubMed.
- A. J. Gianola, T. Ichino, R. L. Hoenigman, S. Kato, V. M. Bierbaum and W. C. Lineberger, J. Phys. Chem. A, 2004, 108, 10326–10335 CrossRef CAS.
- O. Smirnova, Y. Mairesse, S. Patchkovskii, N. Dudovich, D. Villeneuve, P. Corkum and M. Y. Ivanov, Nature, 2009, 460, 972–977 CrossRef CAS PubMed.
- O. Smirnova, S. Patchkovskii, Y. Mairesse, N. Dudovich and M. Y. Ivanov, Proc. Natl. Acad. Sci. U. S. A, 2009, 106, 16556–16561 CrossRef CAS PubMed.
- O. Smirnova, S. Patchkovskii, Y. Mairesse, N. Dudovich, D. Villeneuve, P. Corkum and M. Y. Ivanov, Phys. Rev. Lett., 2009, 102, 063601 CrossRef PubMed.
- Y. Mairesse, J. Higuet, N. Dudovich, D. Shafir, B. Fabre, E. Mével, E. Constant, S. Patchkovskii, Z. Walters and M. Y. Ivanov, et al. , Phys. Rev. Lett., 2010, 104, 213601 CrossRef CAS PubMed.
- S. Haessler, J. Caillat, W. Boutu, C. Giovanetti-Teixeira, T. Ruchon, T. Auguste, Z. Diveki, P. Breger, A. Maquet and B. Carré, et al. , Nat. Phys., 2010, 6, 200–206 CrossRef CAS.
- P. M. Kraus, B. Mignolet, D. Baykusheva, A. Rupenyan, L. Horny, E. Penka, G. Grassi, O. I. Tolstikhin, J. Schneider and F. Jensen, et al. , Science, 2015, 350, 790–795 CrossRef CAS PubMed.
- B. D. Bruner, Z. Mašín, M. Negro, F. Morales, D. Brambila, M. Devetta, D. Faccialà, A. G. Harvey, M. Ivanov, Y. Mairesse, S. Patchkovskii, V. Serbinenko, H. Soifer, S. Stagira, C. Vozzi, N. Dudovich and O. Smirnova, Faraday Discuss., 2016, 194, 369–405 RSC.
- R. Torres, T. Siegel, L. Brugnera, I. Procino, J. G. Underwood, C. Altucci, R. Velotta, E. Springate, C. Froud and I. Turcu, et al. , Phys. Rev. A: At., Mol., Opt. Phys., 2010, 81, 051802 CrossRef.
- R. Cireasa, A. Boguslavskiy, B. Pons, M. Wong, D. Descamps, S. Petit, H. Ruf, N. Thiré, A. Ferré and J. Suarez, et al. , Nat. Phys., 2015, 11, 654–658 CrossRef CAS.
- S. M. Poullain, C. Elkharrat, W. B. Li, K. Veyrinas, J. C. Houver, C. Cornaggia, T. N. Rescigno, R. R. Lucchese and D. Dowek, J. Phys. B: At., Mol. Opt. Phys., 2014, 47, 124024 CrossRef.
- J. Tennyson, Phys. Rep., 2010, 491, 29–76 CrossRef CAS.
- J. M. Carr, P. G. Galiatsatos, J. D. Gorfinkiel, A. G. Harvey, M. A. Lysaght, D. Madden, Z. Mašín, M. Plummer, J. Tennyson and H. N. Varambhia, Eur. Phys. J. D, 2012, 66, 58 CrossRef.
- A. G. Harvey, D. S. Brambila, F. Morales and O. Smirnova, J. Phys. B: At., Mol. Opt. Phys., 2014, 47, 215005 CrossRef.
- D. S. Brambila, A. G. Harvey, Z. Mašín, J. D. Gorfinkiel and O. Smirnova, J. Phys. B: At., Mol. Opt. Phys., 2015, 48, 245101 CrossRef.
- D. M. Hirst, J. Chem. Phys., 2001, 115, 9320–9330 CrossRef CAS.
- V. Kurkal, P. Fleurat-Lessard and R. Schinke, J. Chem. Phys., 2003, 119, 1489–1501 CrossRef CAS.
- H.-J. Werner, P. J. Knowles, G. Knizia, F. R. Manby, M. Schütz, P. Celani, T. Korona, R. Lindh, A. Mitrushenkov, G. Rauhut, K. R. Shamasundar, T. B. Adler, R. D. Amos, A. Bernhardsson, A. Berning, D. L. Cooper, M. J. O. Deegan, A. J. Dobbyn, F. Eckert, E. Goll, C. Hampel, A. Hesselmann, G. Hetzer, T. Hrenar, G. Jansen, C. Köppl, Y. Liu, A. W. Lloyd, R. A. Mata, A. J. May, S. J. McNicholas, W. Meyer, M. E. Mura, A. Nicklass, D. P. O'Neill, P. Palmieri, D. Peng, K. Pflüger, R. Pitzer, M. Reiher, T. Shiozaki, H. Stoll, A. J. Stone, R. Tarroni, T. Thorsteinsson and M. Wang, MOLPRO, version 2012.1, a package of ab initio programs, 2012 Search PubMed.
- A. D. Mclean and G. S. Chandler, J. Chem. Phys., 1980, 72, 5639–5648 CrossRef CAS.
- K. Houfek, http://https://ccpforge.cse.rl.ac.uk/gf/project/ukrmol-scripts/.
- A.-T. Le, R. R. Lucchese, S. Tonzani, T. Morishita and C. D. Lin, Phys. Rev. A: At., Mol., Opt. Phys., 2009, 80, 013401 CrossRef.
- Z. Chen, A.-T. Le, T. Morishita and C. D. Lin, Phys. Rev. A: At., Mol., Opt. Phys., 2009, 79, 033409 CrossRef.
- O. Smirnova and M. Ivanov, Attosecond and XUV Physics, Wiley-VCH Verlag GmbH & Co. KGaA, 2014, pp. 201–256 Search PubMed.
| This journal is © the Owner Societies 2017 |