Corannulene and its complex with water: a tiny cup of water

Abstract

We report the results of a broadband rotational spectroscopic study of corannulene, C₂₀H₁₀, all of its singly substituted ¹³C isotopologues, and a complex of corannulene with one molecule of water. Corannulene is a polycyclic aromatic hydrocarbon (PAH) with a curved structure that results in a large dipole moment. Observation of ¹³C isotopic species in natural abundance allowed us to precisely determine the molecular structure of corannulene. The differences between the experimental C–C bond lengths correlate to the double-bond character predicted using Kekule's resonance structures. In the case of C₂₀H₁₀–H₂O, the water molecule is found to reside inside the bowl-like structure of corannulene. Our experimental and theoretical results indicate that the water molecule rotates freely around its C₂ axis and that dispersion interactions are the dominant contribution to the binding.

---

1 Introduction

Despite much spectroscopic effort, the interstellar role of polycyclic aromatic hydrocarbons (PAHs) is not yet well understood. They are thought to be ubiquitous throughout the interstellar medium (ISM), in a wide variety of environments, and they are proposed to be the source of unidentified infrared (UIR) bands between 3 and 16 μm. From analysis of these bands, it is thought that PAHs account for about 20% of the galactic carbon budget.^1,2

Though their presence has not been confirmed by the unambiguous identification of a single PAH, it is believed that the UIR bands are indicative of the presence of PAHs. Recently, two fullerenes, which are thought to be closely related to PAHs, C₆₀ and C₇₀ were detected in the mid-infrared frequency range in the planetary nebula, Tc1.³ In 2015, Campbell et al. attributed two lines of the diffuse interstellar bands to C₆₀⁺ cations by using laboratory absorption spectroscopy of C₆₀⁺ in the gas phase, cooled to 5.8 Kelvin.⁴ These observations triggered the discussion that PAHs, which could be fullerene precursors, might be more widespread in interstellar space than initially thought. PAHs and fullerenes are chemically connected to each other via hydrogenation and dehydrogenation pathways, potentially involving pseudofullerenes.³ PAHs are also discussed as missing links for the formation of more complex organic molecules in the Universe by providing seeds as starting points of chemical reactions, as formulated in the PAH hypothesis.²

A large fraction of the approximately 200 molecules detected in the ISM were identified via their rotational emission using radio astronomy,^5–7 which allowed for their unambiguous identification. As new radio interferometers, such as the Atacama Large Millimeter/submillimeter Array (ALMA) and the expanded Very Large Array (eVLA), as well as the James Webb Space Telescope for infrared studies come online, there are opportunities for the chemical inventory of the ISM to increase rapidly. These facilities have increased sensitivity and outstanding spatial resolution, and there is a large amount of new radioastronomic data from these instruments. The bottleneck in analyzing these datasets is the lack of laboratory data. The main constraint for pure rotational spectroscopy is the fact that the molecules must have a permanent electric dipole moment. This is not the case with most PAHs, which only have a small or non-existent dipole moment, and this stipulation is only fulfilled by some classes of PAHs, such as substituted species⁸ or PAHs that are not fully aromatic.⁹

An exception to this is corannulene, C₂₀H₁₀.¹⁰ It can be envisioned as the cap of C₆₀, saturated with hydrogen atoms. Corannulene is a fully aromatic PAH with a permanent dipole moment of 2.07 D, as experimentally determined using rotational spectroscopy combined with Stark effect measurements.¹⁰ This extraordinarily large dipole moment originates from its curved shape and makes it a very promising candidate for radioastronomic detection of PAHs in the ISM, even though it is considered to be a small PAH by interstellar standards. However, subsequent radioastronomic searches in the Red Rectangle and TMC-1 were unsuccessful.^11–13

Motivated by the potential role of PAHs in interstellar chemistry, recent developments in radioastronomy and new capabilities of rotational spectroscopy allowed by the advent of broadband chirped pulse rotational spectroscopy (CP-FTMW),¹⁴ we employ CP-FTMW spectroscopy^14,15 to extend the set of available molecular parameters for corannulene. We use the cold and collision free conditions of a molecular jet to extend the previous microwave spectroscopic study on the corannulene monomer to provide a full analysis of this special PAH, including an accurate redetermination of its molecular structure. Moreover, we study the complexation of C₂₀H₁₀ with water, a potential starting point for PAH chemistry and ice formation on dust grains. For the C₂₀H₁₀–water complex, we aim at evaluating the preferred binding position of the water molecule to corannulene – inside the bowl or outside of the bowl – and whether the water molecule would show rotational or translational mobility on the surface provided by corannulene. Precise information on the corannulene–water interaction can be useful for models aiming at describing aerosol and ice grain formation. Independent of an astrochemical interest, this high resolution rotational spectroscopy study of corannulene and its water cluster is also of relevance in its own interest. Corannulene is a rigid, highly symmetric molecule (C_5v point group), and thus exhibits the rotational spectrum of a symmetric top. As a result, the intensity of many rotational transitions is concentrated in a single resolvable spectroscopic line resulting in an intense rotational spectrum.¹⁰

2 Experimental and computational details

All rotational spectroscopy measurements were performed with the Hamburg COMPACT spectrometer, which has been described in detail elsewhere.¹⁶ The molecules were seeded into a supersonic expansion with neon as the carrier gas by using a pulse nozzle (Parker General Valve, Series 9) equipped with a heatable reservoir close to the valve orifice, operating at 4 Hz. Corannulene (C₂₀H₁₀) was purchased from TCI Deutschland GmbH (with a specified purity of more than 97%) and used without further purification. C₂₀H₁₀ is a solid at room temperature; it sublimes at 170 °C (0.02 Torr) and melts at 268–269 °C (under nitrogen). The sample was heated in the reservoir nozzle to around 170 °C in order to generate sufficient vapor pressure for recording the rotational spectrum. Clusters with water were generated by first flowing the carrier gas (neon) through a reservoir containing water that was external to the chamber. After supersonic expansion into vacuum using neon at 2 bar, the molecular jet was polarized with a 4 μs chirp spanning 2–8 GHz. The chirp was generated with an arbitrary waveform generator, amplified to 300 W with a traveling wave tube amplifier, and transmitted into the vacuum chamber via a horn antenna. Following excitation, the free induction decay (FID) of the macroscopic ensemble of polarized molecules was recorded. The fast frame capability¹⁷ of the Tektronix DPO 71254C was used in which eight consecutive excitation chirps, each followed by 50 μs so that the FID could be collected, were recorded and averaged. This resulted in an effective repetition rate of 32 Hz. For the spectrum of the corannulene monomer 2.5 million FIDs were coadded, and for the corannulene–water complex 4.1 million FIDs were coadded. Fourier transformation of the averaged time domain FID, recorded at point spacings of 10 ps, resulted in a frequency domain rotational spectrum with frequency resolution of 25 kHz. The intensity of the monomer spectrum was sufficient to observe the spectra of all ¹³C singly substituted species (see below) in addition to that of the parent isotopologue.

The experimental results were complemented by and compared with electronic structure calculations. M06-2X/cc-pVDZ, M06-2X/6-311++G(d,p) and conventional MP2/6-311++G(d,p) calculations were performed using the Gaussian 09, rev. D.01¹⁸ program suite to assess the sensitivity of the predictions to the choice of method and basis set. Symmetry adapted perturbation theory (SAPT) calculations¹⁹ in the PSI4 package²⁰ were used to investigate the intermolecular interactions for the corannulene–water complex. The binding energy of the dimers E_d was determined with density fitted MP2 (RI-MP2) at 6-311++G**, aug-cc-pVDZ and aug-cc-pVTZ basis sets using the ORCA 3.0.3 software package.²¹ Because basis set superposition error (BSSE) can be large for binding energies of non-covalently bonded clusters, we also determined the counterpoise (CP)²² corrected binding energy. While the uncorrected energy often overbinds the clusters and the CP corrected one underbinds, the true binding energy falls somewhere between the uncorrected and CP corrected values. A more robust way to overcome BSSE as well as basis set incompleteness error (BSIE) is to use explicitly correlated methods. One such method, RI-MP2-F12,²³ is implemented efficiently with the 3C(FIX) ansatz²⁴ in the Molpro 2015 package.²⁵ At the RI-MP2 optimized geometry, we calculated the RI-MP2-F12 energy with the cc-pVTZ-F12 (VTZ-F12) orbital basis with aVTZ/JKFIT DH-HF fitting basis, aVTZ/MP2FIT DF-MP2 fitting basis, VTZ-F12/OPTRI complementary auxiliary basis set (CABS).

3 Results and discussion

3.1 Rotational spectroscopy of corannulene

The high-resolution broadband rotational spectrum obtained for the corannulene monomer is displayed in Fig. 1. Corannulene is an oblate symmetric top of C_5v symmetry and gives rise to a simple, characteristic spectrum. Five ΔJ = 1 rotational transitions were observed for the parent monomer (with J being the total angular momentum quantum number), and their assignment is indicated in the top panel of Fig. 1. In accordance with ref. 10, no K substructure was observed, with K being the quantum number associated with rotation about the principal rotation axis of the molecule. Previously, 15 rotational transitions between 5–20 GHz were recorded, and a set of rotational constants were obtained from fitting a symmetric-top Hamiltonian to the experimental transition frequencies.¹⁰ The results of jointly fitting these previous transitions with the newly obtained low-frequency transitions from the present CP-FTMW spectroscopy study are summarized in Table 1. Line lists are given in Table S1 of the ESI.† The low-frequency range of our spectrometer enabled us to extend the dataset down to 3 GHz. The molecule is very rigid, as evidenced by the small experimentally determined centrifugal distortion constant D_J, even though transitions up to J = 19 are included.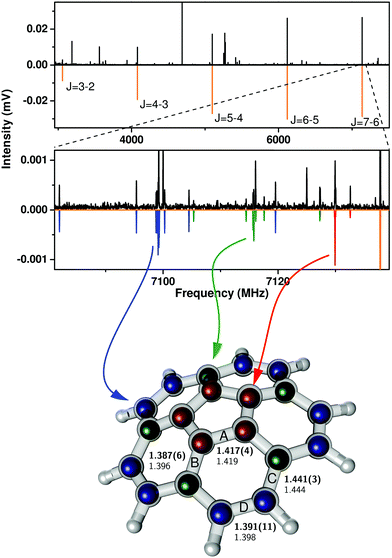

Fig. 1 Broadband rotational spectrum of corannulene (top panel) and its zoom illustrating rotational transitions from singly substituted ¹³C isotopologues (middle panel) (top traces: experimental data, lower traces: simulations based on spectral fits, Table 1). Rotational transitions arising from all three possible isotopologues, corresponding to substitution in the inner, middle, and outer carbon position, have been assigned and are indicated by the color code. On the bottom, the experimentally determined atom positions (colored balls) and the numerical values for the four distinct C–C bonds, labeled A–D, from the present study (upper number) are compared with those from an MP2/6-311++G(d,p) calculation (lower number).

Table 1 The fitted spectroscopic constants for the parent and for all three possible singly substituted ¹³C isotopologues of the corannulene monomer

	Parent		^13Co (outer)	^13Cm (middle)	^13Ci (inner)
	Exp.^a	Calc.^b
a Current measurements combined with those from ref. 10. b DFT calculation at the M06-2X/cc-pVDZ level. c Calculated from the planar moment Pb(^13Co) = 954.77(44) uÅ^2 for the ^13Co species and Ic = 2Pb(^13Co) − Ia + Ib, where Ia and Ib are the moments of inertia for this species. d C = 263.74(60) MHz, if used as a parameter of fit. e Assumed value, taken from the parent species. f The number of fitted transitions. g Standard deviation of the fit.
A (MHz)			509.80864(26)	509.84975(41)	509.65615(73)
B (MHz)	509.842688(16)	509.72	504.41888(24)	506.70892(41)	508.90885(79)
C (MHz)	[264.66]^c	264.49	263.20(12)	[263.81]^c^,^d	[264.46]^c
D J (kHz)	0.004364(46)		[0.004364]^e	[0.004364]^e	[0.004364]^e
D JK (kHz)			0.083(21)
N	20		31	25	13
σ (kHz)	2.62		4.69	6.50	9.92

---

A zoom into the broadband spectrum, as shown in the middle part of Fig. 1, illustrates the J = 7–6 spectra of the three ¹³C isotopologues in natural abundance. The ¹³C isotopic lines are represented by the color code in which the red trace corresponds to isotopic substitution of a carbon atom C_i in the inner pentagon (five-fold degenerate due to C_5v symmetry). The green trace corresponds to substitution of a carbon atom C_m in the intermediate circle (also five-fold degenerate), and the blue trace identifies the spectrum resulting from substitution of C_o, a carbon atom in the outer circle, which is ten-fold degenerate due to a combination of C₅ and σ_v symmetry operations. As the zoomed-in spectrum in Fig. 1 shows, the transition frequencies are shifted to lower frequency in relation to the parent in proportion to increasing distance of the substituted carbon atom from the molecular center of mass. The isotopic spectra for single ¹³C substitution are somewhat easier to observe than in other species since the high symmetry of corannulene leads to natural abundance spectra that are enhanced by a factor of five for ¹³C_i and ¹³C_m substitution, and a factor of ten for the ¹³C_o isotopologue. A ¹³C substitution reduces the symmetry of the molecule from an oblate symmetric top to that of a near-oblate asymmetric top. This lower symmetry leads to K-type splitting in the spectra, which is the most pronounced for the ¹³C_o isotopologue (¹³C substitution in the outer ring, blue trace in Fig. 1). Only for this ¹³C_o isotopologue is the asymmetry splitting sufficiently large to allow for the determination of all three rotational constants. The standard assumption of isotopic invariance of molecular geometry then allowed us to use these constants to calculate the axial rotational constant C for the other isotopic species. This is possible since the ¹³C atom is in the ac-inertial plane for the substitution positions, so that the planar moment 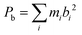(where m_i are atomic masses, and b_i their b-principal axis coordinates) is the same for all of the measured isotopic species and thus equal to the value for the parent species.

The experimentally determined rotational constants of the three different ¹³C isotopologues are also summarized in Table 1 and the experimental frequencies are reported in Tables S2–S4 (ESI†). We find that the DFT calculation at the M06-2X/cc-pVDZ is fortuitous at reproducing the ground state rotational B constant for corannulene, as well as the C constant estimated from the value of P_b(¹³C_o).

The corannulene bowl is relatively shallow so that it can be subject to a motion inverting the bowl. Experimental investigations by NMR spectroscopy indicated that in solution this motion can occur at a rate of 200 kHz under room temperature conditions,²⁶ yet both experiment²⁶ and calculations²⁷ estimate the barrier to this motion to be well over 40 kJ mol⁻¹. The inversion motion is arrested in the crystal and has not yet been observed in the gas phase, including our present spectra. The signature of such a motion in rotational transitions would be a characteristic equal intensity line doubling resulting from inversion splitting of the ground vibrational state. Nevertheless, the magnitude of this splitting is inversely proportional to the barrier and to the reduced mass for the inversion motion. For corannulene both are much too high for such splitting to be resolved. Phrased differently, on the timescale of the experiment (a few tens of μs), no interconversion takes place, in accordance with previous gas-phase results.

3.2 Structure of corannulene

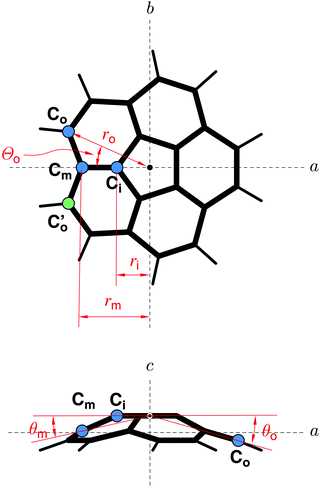
The high molecular symmetry of corannulene reduces the amount of the available spectroscopic information, but it also considerably reduces the number of independent structural parameters. In C₂₀H₁₀, there are only four distinct C–C bonds, indicated by A–D in the structure in the bottom part of Fig. 1. These are the C–C bonds in the central pentagon (denoted by A), the bonds between an inner carbon atom and a carbon atom in the middle ring (denoted by B), the bonds between a middle carbon atom and a carbon atom in the outer ring (denoted by C), and finally bonds connecting two outer carbon atoms (denoted D), which are connected to hydrogen atoms as well.

As has been demonstrated for another higher-symmetry molecular species, namely cyclohexane,²⁸ the relatively small number of measured isotopologues is not prohibitive to the determination of a reliable molecular geometry. This is providing that full advantage is taken of the molecular symmetry. The resulting r₀ geometry determined for the D_3d-symmetric cyclohexane was used to predict the value of the difficult to determine axial rotational constant, which was later confirmed by femtosecond rotational coherence spectroscopy.²⁹ In the case of corannulene it turns out that only six independent structural parameters are needed to describe the carbon skeleton, when these parameters are defined in a centrosymmetric declaration as shown in Fig. 2. Another three structural parameters are required for the C–H bonds. A least squares fit of these parameters to all of the available experimental data can be conveniently set up using the STRFIT program,³⁰ freely available on the PROSPE website.^31,32 The primary results of such a fit are given in Table S5 (ESI†). The fitted centrosymmetric parameters and their uncertainties have been converted into the chemically relevant structural parameters with the program EVAL (also on the PROSPE website) and are listed in Table 2. This table allows a comparison with other experimental results and with quantum chemistry calculations. Prior to discussing the actual values it should be noted that the present rotational data were insufficient to determine all nine structural parameters that define the complete structure of corannulene. For this reason we made some judicious assumptions concerning three of those parameters. The values in square brackets in Table 2 have been fixed to the average of the two cited quantum chemistry calculations. We note that a much broader range of calculations resulted in very similar values for these parameters. The two angles associated with the C–H bonds were found to have a minimal effect on the results of the structural fit, for example an uncertainty of 0.3° in their values added much less than 10% to the deviations of the parameters of the fit. It is only the dihedral angle Θ_o for the outer carbon atom that turned out to be critical, primarily for the uncertainty in bond D. The uncertainty for this bond as cited in Table 2 accounts for an assumed ±0.1° uncertainty in Θ_o, which encompasses the range of values seen in DFT and ab initio calculations.

Fig. 2 The six unique structural coordinates defining the carbon skeleton of corannulene: the distance r_i of the inner carbon C_i from the centre of the pentagon, the distance r_m and the angle θ_m for the intermediate carbon C_m, and the distance r_o, the angle θ_o, and the dihedral angle Θ_o for the outer carbon atom C_o. Other members of the C_i, C_m, and C_o atom subsets are generated by means of the C₅ symmetry operation, while C_o′ atoms are generated from the C_o atoms by means of a reflection about the ac plane.

Table 2 Structural parameters (Å and degree) of corannulene from MW (this work), GED,³³ X-ray³⁴ and calculations (employing the 6-311++G(d,p) basis set) and comparison with the estimated double-bond (DB) character according to Kekule's resonance structures

Parameter		MW, r0	GED, rα	X-ray^a	Calculated, re		DB character
		This work	Ref. 33	Ref. 34	MP2	M06-2X
a Average values over chemically equivalent parameters in two crystallographically independent molecules. b The cited uncertainty is a single standard deviation. c The angle between the plane containing Co and the c-inertial axis and the plane containing Cm and the c-inertial axis. d Assumed value, fixed to the average of the two respective quantum-chemical calculations, see text.
A	r(CiCi)	1.417(4)^b	1.410(3)	1.413(2)	1.419	1.416	0.27
B	r(CiCm)	1.387(6)	1.408(10)	1.391(4)	1.396	1.376	0.46
C	r(CmCo)	1.441(3)	1.441(8)	1.440(2)	1.444	1.446	0.27
D	r(CoCo)	1.391(11)	1.374(8)	1.402(5)	1.398	1.380	0.73
∠(A–B)	∠(CiCiCm)	122.6(3)	122.4(3)	123.0(2)	122.5	122.8
∠(B–C)	∠(CiCmCo)	114.5(3)	113.9(3)	114.3(1)	114.9	114.6
∠(C–D)	∠(CmCoCo)	121.9(2)	122.4(2)	122.0(2)	121.8	121.9
	Θ o	[23.66]^d			23.59	23.73
	r(CH)	1.101(14)	1.112(9)	1.01(1)	1.089	1.085
	∠(HCoCo)	[118.45]^d	118.2(1)	120.(1)	118.32	118.58
	Θ(HCoCoCm)	[174.13]^d			174.02	174.23

---

It should be noted that the geometries for corannulene in Table 2 all have a slightly different physical meaning. Thus they can only be compared in an approximate manner. The present geometry (MW, r₀) pertains to the ground vibrational state, the gas phase electron diffraction (GED) geometry³³ includes harmonic vibration–rotation contributions, while the X-ray geometry³⁴ results from averaging over many unequal values in two crystallographically independent molecules. The calculated geometries are equilibrium geometries, r_e, at the minimum of the molecular potential. With these caveats in mind we note from Table 2 that the current determination is in closest agreement with quantum chemistry calculations, as summarised also in Fig. 1. The agreement concerns not only the C–C bond lengths, but also the angles, which are all in good correlation with the calculated values.

It turns out that the relative C–C bond lengths can be usefully rationalised in terms of classical resonance structures. Taking into account the three possible Kekule type resonance structures and their multiplicities as discussed in ref. 33, the fraction of double-bond character (DB) for the individual bonds A, B, C, and D is 0.27, 0.46, 0.27, and 0.73, respectively. This approach thus predicts that bond D is the shortest, while bonds A and C are predicted to be the longest. Bond B is predicted to be of intermediate length, which is in fair agreement with our experimental findings. This is despite the fact that we observe bonds B and D to be of similar length. It is intriguing that the relative values of the bond lengths predicted by the basic concept of resonance among Kekule structures are in such a good agreement with the experimental structure for this nonplanar, aromatic molecule. It also turned out that the rotational spectroscopy data allows fitting C–H bond length and, even though it is not particularly precise, is at a typically larger value than the calculated equilibrium distances.

We note that there are some discrepancies between the various sets of values in Table 2. The Kekule picture can only be taken so far since the weight of experimental and computational evidence points to bond A being significantly shorter than bond C, even though both have the same DB character. Also bond B from the GED study appears to be longer (and comparable to bond A), which is perhaps due to the greatest uncertainty in the GED determination of the length of bond B. In contrast, the structure determination of crystalline C₂₀H₁₀ using X-ray diffraction results in a similar alternation in bond lengths and angles as in the microwave and quantum-chemical data, but with different absolute values. This is most likely due to packing effects in the crystal.³⁴

3.3 Corannulene–water complex

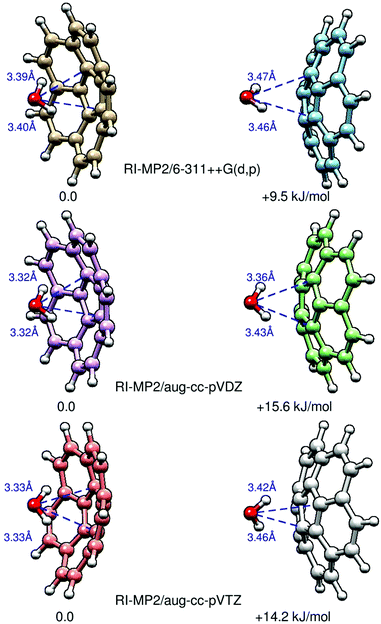
In order to elucidate the preferred binding position of water on the corannulene surface, we recorded the rotational spectrum of the corannulene–water complex. There are two potential binding motifs: to the inside of the bowl (C₂₀H₁₀–w-in) or on the outside (C₂₀H₁₀–w-out). Ab initio calculations at the MP2 level of theory reveal that C₂₀H₁₀–w-in is the favored configuration of the complex and approximately 10 kJ mol⁻¹ lower in energy than C₂₀H₁₀–w-out (see Fig. 3 and Table 3). In Fig. 3, we present results of three different theoretical approaches for the two isomers, and we highlight their energy differences ΔE. Note that these structures are C₁-symmetric, with non-zero dipole-moment components μ_a and μ_b, even when performing the calculations using tight convergence criteria. The distances of the water oxygen to the nearest carbon atom (R_OCi) are also given. We find that the respective bonds for the C₂₀H₁₀–w-in complex are always shorter than for those in the C₂₀H₁₀–w-out complex. Structures in which water is interacting with one or several of the hydrogen atoms of corannulene are found to be irrelevant.

Fig. 3 The structures for the two isomers of the corannulene–water complex, C₂₀H₁₀–w-in (left) and C₂₀H₁₀–w-out (right), calculated at the RI-MP2 level of theory with different basis sets. The relative energies ΔE are given, and the closest oxygen–carbon distances R_OCi are marked.

Table 3 Spectroscopic and molecular parameters obtained from a global analysis (including both internal rotation states m = 0 and m = 1) of the symmetric-top spectrum of the observed corannulene–water cluster, C₂₀H₁₀–w-in, and comparison with results from ab initio calculations at the MP2/6-311++G(d,p) level of theory. E_d is the binding energy, which is counterpoise-corrected for the calculated values, and ΔE defines the relative energies of the two isomers

	Exp.	Calculated
		In	Out
a The value estimated for free corannulene, see Table 1. b Distance estimated by using the pseudo-diatomic model, see text. c Distance derived from Rcm by assuming the C20H10–w-in geometry. d Distance derived from Rcm by assuming the C20H10–w-out geometry. e Negative of Lennard-Jones well depth from the pseudo-diatomic model.
A (MHz)		460.8	407.9
B (MHz)	455.597043(55)	460.5	407.6
C (MHz)	264.66^a	265.3	264.2
D J (kHz)	0.02013(57)
D Jm (MHz)	4.306704(78)
H Jm (kHz)	0.00801(81)
|μa| (D)		0.23	0.02
|μb| (D)		0.29	0.02
|μc| (D)		0.51	5.1
μ tot (D)		0.63	5.1
R cm (Å)	2.640^b	2.468	3.804
R Ox (Å)	3.318,^c 2.094^d	3.179	3.240
R OCi (Å)	3.531,^c 2.416^d	3.399	3.447
E d (kJ mol^−1)	−12.0^e	−17.8	−11.3
ΔE (kJ mol^−1)		0	+6.5

---

The observed rotational spectrum of the complex is that of an oblate symmetric top with no K-substructure, just as observed for free corannulene. This is contrary to our initial expectation that addition of a water molecule would break the high symmetry of corannulene and thus lead to an asymmetric rotor spectrum. The rotational spectrum of the corannulene–water complex only exhibits c-type transitions (i.e., interacting with the μ_c dipole moment component of the complex and following the selection rules J + 1_Ka+1,Kc ← J_Ka,Kc). It shows a characteristic fine structure, in which, every rotational transition is split into two components that are caused by the internal motion of the water molecule relative to corannulene. These two sets of rotational transitions can be attributed to two free-rotor states specified by the quantum number m = 0, ±1,… Both the m = 0 and the m = 1 transitions appear as symmetric tops. This situation is very similar to the one described and treated for the benzene–water complex.^35,36 In that case a double symmetric-top spectrum was also observed, and rationalised by means of a low-barrier or even barrier-less internal rotation of the water molecule about the sixfold symmetry axis of benzene.

In general, internal rotation theory predicts symmetric-top spectra for coaxial rotors of at least three-fold and two-fold symmetry with a small effective barrier. As in the benzene–water complex, we used the treatment originally pioneered for the weakly bound cluster CF₃H–NH₃,³⁷ allowing a global fit of transitions for both internal rotation substates. Such a global fit provides us with detailed experimental information about the structure and internal dynamics of the complex. The fit is based on the symmetric-top Hamiltonian³⁷ inclusive of free internal rotation terms, such that the transition frequencies are described by ν(J,m) = 2(J + 1)[B − D_Jmm²] − 4(J + 1)³[D_J + H_Jmm²]. Here, the quantum number m = 0, ±1,… specifies the internal rotation state, as mentioned above, and D_J, D_Jm, and H_Jm are centrifugal distortion constants. The results of this fit are summarised in Table 3, and the observed transition frequencies are given in Table S6 of the ESI.†

The experimental rotational constants can be directly compared with the results from ab initio calculations (MP2/6-311++G(d,p) level of theory), which are also included in Table 3. Note that theory predicts the complex to be slightly asymmetric, with the rotational constants A and B differing by several hundred kHz. It is, therefore, possible that the reported constant B may actually be equivalent to (A + B)/2 in the presence of some vibrational averaging of the water motion in the cluster. The calculated rotational constants for the two different isomers differ by about 50 MHz. Similar results are obtained at RI-MP2/aug-cc-pVDZ and RI-MP2/aug-cc-pVTZ and even with DFT using M06-2X/6-311++G(d,p) (see Table S7 of the ESI†). The experimentally determined rotational constant B = 455.597043(55) MHz is close to the calculated values for the C₂₀H₁₀–w-in isomer, and this is the lower energy isomer (Fig. 3). C₂₀H₁₀–w-out is assumed to be invisible in the CP-FTMW experiment due to insufficient population in our supersonic expansion using neon carrier gas.

While the rotational constants for the two isomers differ by only about 50 MHz, the magnitudes of their dipole moments have the most notable difference. C₂₀H₁₀–w-out has a large overall dipole moment, arising from the large μ_c component. This component is significantly smaller for C₂₀H₁₀–w-in. This difference can be easily explained by the orientation of the molecules in the complex with respect to each other, as dipole moments are additive. For both isomers, the symmetry axes of the water and the corannulene monomers are almost coaxial with the c internal axis (see Fig. 4). For C₂₀H₁₀–w-out, their respective dipole moments (2.07 D for corannulene and 1.85 D for water) point in the same direction. This explains the large value of the μ_c component (approximately 5 D) with only negligible values for μ_a and μ_b (Table 3). For C₂₀H₁₀–w-in, the corannulene and water symmetry axes are likewise nearly coaxial with the internal axis c, but predicted to be slightly tilted, causing nonzero values for μ_a and μ_b.

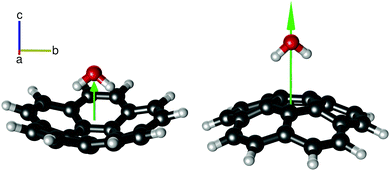Fig. 4 The two isomers of the corannulene–water complex: C₂₀H₁₀–w-in (left) and C₂₀H₁₀–w-out (right). C₂₀H₁₀–w-out is calculated to be 10–15 kJ mol⁻¹ higher in energy than C₂₀H₁₀–w-in (Fig. 3). The green arrow qualitatively indicates the magnitude of the μ_c dipole moment component. For C₂₀H₁₀–w-out, this value is significantly larger because the respective dipole-moment components add up constructively. For both isomers, the C₂ symmetry axis of the water and the C₅ symmetry axis of corannulene almost coincide. The higher stability of the lower dipole moment conformer is a direct indicator that electrostatic interactions are not dominant in the intermolecular interaction between the two molecules.

Most importantly, however, the dipole moments of water and corannulene point in almost opposite directions and therefore partially cancel, resulting in a small μ_c value in the region of 0.5 D. The contributions from μ_a and μ_b are sensitive to the relative orientations of the symmetry axes of water and corannulene with respect to each other. It is thus not surprising that different theoretical levels provide somewhat different calculated μ_a and μ_b values, as reported in Table S7 (ESI†). Note that despite an extensive search, only c-type transitions have been observed experimentally. The missing a- and b-type transitions further support our analysis that low-barrier internal motion of the water molecule with respect to corannulene leads to the average structure of a symmetric top, with vanishingly small μ_a and μ_b dipole moment components.

The combination of experimental and theoretical results allows us to conclude the complex structure is that of the C₂₀H₁₀–w-in complex. The experimental results, even when limited to a single rotational constant and a single centrifugal distortion constant for the cluster, still allow useful information to be derived by means of the pseudo diatomic model. The model was first applied to weakly bound clusters in connection with Ar–HCl³⁸ and was later extended by a succession of refinements taking into account various departures of complexed molecules from simple diatomic symmetry.^39–42 The most useful relations from these papers have been embodied in the computer program DJ, recently added to the PROSPE website.

In the present case, the most useful result of the pseudo-diatomic model is the determination of the centre of mass separation, R_cm, of the clustered molecules from the rotational constants of the cluster and of the constituent molecules (eqn (17), ref. 42). The knowledge of the monomer geometries then allows the determination of the effective distance R_Ox between the water oxygen atom and the plane of the central carbon pentagon of corannulene, as well as of the shortest O–C distance. The model leads to R_cm = 2.640 Å for both C₂₀H₁₀–w-in and C₂₀H₁₀–w-out. A similar determination can be carried out with the STRFIT program by using the r₀ geometries of water⁴³ and of corannulene (as determined above), resulting in R_cm = 2.637 Å. Unambiguous distinction between the in and out conformations is now possible by comparing the R_cm distance and the derived distances with calculations. The comparison makes it clear that the C₂₀H₁₀–w-in isomer has been observed as the R_cm for the out isomer would be expected to be considerably larger. This is primarily due to the fact that in both isomers the water molecule attaches to corannulene at a distance close to the sum of van der Waals radii of oxygen and carbon (3.22 Å, ref. 44). For the out isomer this separation leads to calculated R_cm = 3.80 Å, which is much larger than the experimental value. Conversely, if the experimental value of R_cm is interpreted in terms of the out isomer then it leads to R_OCi = 2.42 Å, which is untenable in view of known van der Waals radii of these atoms. The underlying reason for such a clear distinction is the bowl shape of corannulene, which results in its centre of mass being distant by 0.61 Å from the plane of the central pentagon.

The pseudo-diatomic model can deliver another useful quantity, namely the well depth obtained by approximating the interaction potential with the 6–12 Lennard-Jones potential. The estimate involves calculation of the intermolecular stretching force constant from the centrifugal distortion constant D_J⁴² followed by correction of the rotational constant of the dimer to equilibrium.^39,41 The procedure and intermediate values are detailed in Table S7 and explored further in Table S8 (ESI†). Considering the assumptive character of the pseudo-diatomic model, the resulting Lennard-Jones well depth of 12 kJ mol⁻¹ compares reasonably with the computed dimerisation energies E_d listed in Table 3 and in Table S7 (ESI†), even though we note that E_d values up to 28 kJ mol⁻¹ have been computed (Table S7, ESI†).

The value R_Ox = 3.32 Å for corannulene water can be compared to the oxygen-ring distance of R_Ox = 3.40 Å and R_OC = 3.60 Å for the benzene–water cluster. These values have been estimated from R_cm = 3.329 Å,³⁶ with the assumption that the water hydrogens are directed towards the ring. The interatomic distances appear to be weakly indicative of a stronger interaction energy in the case of C₂₀H₁₀–w-in compared to benzene–water. Evaluation of the Lennard-Jones well depth for benzene–water gives 8.3 kJ mol⁻¹ compared to 12 kJ mol⁻¹ for corannulene–water, in line with comparison of the calculated interaction energies reported in Table 4 below.

Table 4 SAPT analysis (SAPT2+3/aug-cc-pVDZ, all values in kJ mol⁻¹) for the two C₂₀H₁₀–H₂O isomers, in comparison with the water dimer, (H₂O)₂, and the benzene–water complex

Molecule	Electrostatics	Induction	Dispersion	Exchange	Total
C20H10–w-in	−16.05	−10.37	−37.41	+40.63	−22.40
C20H10–w-out	−12.16	−5.64	−20.27	+25.71	−12.33
(H2O)2	−34.15	−10.37	−9.49	+35.0	−19.06
C6H6–H2O	−13.29	−5.52	−14.50	+21.23	−12.08

---

We also note that a straightforward application of the pseudo-diatomic model using just point masses for the monomers leads to spurious results, including R_cm = 8.1 Å. This is due to the considerable disk-like mass distribution in corannulene, which is oriented perpendicular to the intermolecular interaction axis. A similar effect is visible for benzene–water where R_cm evaluated with an uncorrected formula is 0.8 Å greater than with an appropriate correction. This effect was not noticeable, for example, in clusters of hydrogen halides with rare gas atoms.

3.4 Decomposition of interaction energy for corannulene–water

An informative picture of the energetics of the intermolecular interaction is possible upon its decomposition into physically meaningful constituents. A picture of this underlying energetics was obtained for corannulene–water and related dimers by using symmetry adapted perturbation theory at the SAPT2+3/aug-cc-pVDZ level. The resulting values are listed in Table 4. For the C₂₀H₁₀–w-in isomer, the interaction energy is calculated to be 22.4 kJ mol⁻¹ and thus it is in moderate agreement with the E_d value derived using the pseudo-diatomic model (Table 3). It is noteworthy that the values for corannulene–water and the water dimer are of the same order of magnitude. However, in the case of C₂₀H₁₀–w-in, dispersion interactions are the dominant attractive component, whereas electrostatic interactions dominate in the water dimer. In Table 4, we also included values for the benzene–water complex. For this complex, electrostatic and dispersion interactions contribute almost equally to the overall interaction energy.

Dispersion interactions are not very directional, which further supports the inference that the water molecule can rotate almost freely on the C₂₀H₁₀ surface. Note that the potential energy surface of the corannulene–water complex is very flat with a broad minimum (see Fig. S1 of the ESI†). RI-MP2/6-311++G(d,p) calculations were employed to calculate the barrier to water rotation around its C₂ axis in C₂₀H₁₀–w-in, which was determined to be significantly below 1 kJ mol⁻¹. Such a small value becomes meaningless when zero-point effects are included. Thus, the water molecule can rotate almost freely inside the corannulene bowl, resulting in an average structure. This picture is in agreement with the discussion above.

Together, the experimental and theoretical results draw a coherent picture of the structure and internal dynamics of the C₂₀H₁₀–w-in complex, which has an oblate symmetric-top spectrum for both internal-rotation states m = 0 and m = 1, with both states exhibiting only c-type transitions. This is in agreement with a low-barrier internal rotation of the water molecule around its C₂ axis, which is near coincident with the C₅ symmetry axis of corannulene.

4 Summary and conclusions

In summary, we used broadband rotational spectroscopy to study the C_5v-symmetry PAH corannulene, C₂₀H₁₀, and its complex with water. The high measurement speed and sensitivity of our instrument allowed us to record the singly substituted ¹³C isotopologues of C₂₀H₁₀ in natural abundance. These spectra were then exploited to accurately determine its structure. A comparison with Kekule resonance structures shows good agreement, despite the size and curved structure of corannulene.

In the complex of corannulene with water, the water molecule is found to reside inside the corannulene bowl. A complex in which the water resides on the outside of the bowl is calculated to be about 10 kJ mol⁻¹ higher in energy and is therefore, despite its higher dipole moment, not observed in our spectra. The rotational spectrum of the water complex follows that of a symmetric top and shows a characteristic fine structure. These features arise from the internal motion of the water molecule with respect to the corannulene. Our experimental and theoretical results clearly show that the water molecule rotates almost freely inside the water bowl around its C₂ axis, which almost coincides with the C₅ symmetry axis of corannulene. The binding energy is approximately 20 kJ mol⁻¹ and is thus comparable to that of the water dimer. Even though that is the case, the dominant interaction type in the corannulene–water complex is mainly dispersion interactions, while for the water dimer it is mainly electrostatic.

We find that the structure and internal dynamics of the corannulene–water complex are very similar to those observed for the benzene–water complex. In both spectra, a symmetric-top rotational spectrum indicating (almost) free internal rotation was observed. This behavior is intimately related to the high symmetry of the aromatic binding partner and the fact that the rotation axis of the water has to coincide with the symmetry axis of the aromatic species. For other PAH–water complexes that we are studying in parallel, i.e. those of acenaphthene and fluorene, which are of lower symmetry, such behavior is not observed.

Acknowledgements

This work was performed as part of our activities within the framework of the ERC Starting grant ‘Astrorot’, grant agreement number 638027. It has also been supported by the Deutsche Forschungsgemeinschaft within the priority program SPP1807 (Schnell1280/4-1) and by the excellence cluster ‘The Hamburg Centre for Ultrafast Imaging – Structure, Dynamics and Control of Matter at the Atomic Scale’ of the Deutsche Forschungsgemeinschaft via a Mildred Dresselhaus Guest Professorship for A. M. R. and a Louise Johnson Fellowship for A. L. S., B. T. and G. C. S. acknowledge support by NSF grants CHE-1213521 and CHE-1508556, and by NSF grant CHE-1229354 as part of the MERCURY high-performance computer consortium, while Z. K. acknowledges financial support from a grant from the Polish National Science Centre, decision number DEC/2011/02/A/ST2/00298. J. C. L. acknowledges a Mobility Grant (PRX14/00695) of the Ministerio de Educacion, Cultura y Deporte (Spain) and Dr M. Schnell for her kind hospitality.

References

1. O. Berne and A. G. G. M. Tielens, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 401–406.
2. A. G. G. M. Tielens, Annu. Rev. Astron. Astrophys., 2008, 46, 289–337.
3. W. W. Duley and A. Hu, Fullerenes and proto-fullerenes in interstellar carbon dust, Astrophys. J., 2012, 659, L11.
4. E. K. Campbell, M. Holz, D. Gerlich and J. P. Maier, Laboratory confirmation of C₆₀⁺ as the carrier of two diffuse interstellar bands, Nature, 2015, 523, 322–323.
5. http://https://www.astro.uni-koeln.de/cdms, The Cologne Database for Molecular Spectroscopy (CDMS).
6. H. S. P. Müller, S. Thorwirth, D. A. Roth and G. Winnewisser, Astron. Astrophys., 2001, 370, L49–L52.
7. H. S. P. Müller, F. Schlöder, J. Stutzki and G. Winnewisser, J. Mol. Struct., 2005, 742, 215–227.
8. D. McNaughton, P. D. Godfrey, R. D. Brown, S. Thorwirth and J.-U. Grabow, FT-MW and Millimeter Wave Spectroscopy of PANHs: Phenanthridine, Acridine, and 1,10-Phenanthroline, Astrophys. J., 2008, 6780(1), 309.
9. S. Thorwirth, P. Theule, C. A. Gottlieb, M. C. McCarthy and P. Thaddeus, Rotational Spectra of Small PAHs: Acenaphthene, Acenaphthylene, Azulene, and Fluorene, Astrophys. J., 2007, 6620(2), 1309.
10. F. J. Lovas, R. J. McMahon, J.-U. Grabow, M. Schnell, J. Mack, L. T. Scott and R. L. Kuczkowski, Interstellar chemistry: A strategy for detecting polycyclic aromatic hydrocarbons in space, J. Am. Chem. Soc., 2005, 1270(12), 4345–4349.
11. P. Thaddeus, The prebiotic molecules observed in the interstellar gas, Philos. Trans. R. Soc., 2006, 361, 1681–1687.
12. P. Pilleri, D. Herberth, T. F. Giesen, M. Gerin, C. Joblin, G. Mulas, G. Malloci, J.-U. Grabow, S. Brünken, L. Surin, B. D. Steinberg, K. R. Curtis and L. T. Scott, Search for corannulene (C₂₀H₁₀) in the red rectangle, Mon. Not. R. Astron. Soc., 2009, 3970(2), 1053–1060.
13. W. Klemperer, Astronomical chemistry, Annu. Rev. Phys. Chem., 2011, 620(1), 173–184.
14. G. G. Brown, B. C. Dian, K. O. Douglass, S. M. Geyer, S. T. Shipman and B. H. Pate, A broadband Fourier transform microwave spectrometer based on chirped pulse excitation, Rev. Sci. Instrum., 2008, 79(5), 053103.
15. M. Schnell, Broadband Rotational Spectroscopy for Molecular Structure and Dynamics Studies, Z. Phys. Chem., 2013, 227, 1–21.
16. D. Schmitz, V. A. Shubert, T. Betz and M. Schnell, Multi-resonance effects within a single chirp in broadband rotational spectroscopy: The rapid adiabatic passage regime for benzonitrile, J. Mol. Spectrosc., 2012, 280, 77–84.
17. C. Perez, S. Lobsiger, N. A. Seifert, D. P. Zaleski, B. Temelso, G. C. Shields, Z. Kisiel and B. H. Pate, Broadband fourier transform rotational spectroscopy for structure determination: The water heptamer, Chem. Phys. Lett., 2013, 571, 1–15.
18. G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, J. A. Montgomery, T. Vreven, K. N. Kudin, J. C. Burant, J. M. Millam, S. S. Iyengar, J. Tomasi, V. Barone, B. Mennucci, M. Cossi, G. Scalmani, N. Rega, G. A. Petersson, H. Nakatsuji, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, M. Klene, X. Li, J. E. Knox, H. P. Hratchian, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, P. Y. Ayala, K. Morokuma, G. A. Voth, P. Salvador, J. J. Dannenberg, V. G. Zakrzewski, S. Dapprich, A. D. Daniels, M. C. Strain, O. Farkas, D. K. Malick, A. D. Rabuck, K. Raghavachari, J. B. Foresman, J. V. Ortiz, Q. Cui, A. G. Baboul, S. Clifford, J. Cioslowski, B. B. Stefanov, G. Liu, A. Liashenko, P. Piskorz, I. Komaromi, R. L. Martin, D. J. Fox, T. Keith, M. A. Al-Laham, C. Y. Peng, A. Nanayakkara, M. Challacombe, P. M. W. Gill, B. Johnson, W. Chen, M. W. Wong, C. Gonzalez, J. A. Pople and M. J. Frisch, Gaussian 09, revision d.01, Gaussian Inc., Wallingford, CT, 2009.
19. B. Jeziorski, R. Moszynski and K. Szalewicz, Perturbation theory approach to intermolecular potential energy surfaces of van der Waals complexes, Chem. Rev., 1994, 94, 1887–1930.
20. A. C. Simmonett, R. M. Parrish, E. G. Hohenstein, F. A. Evangelista, J. T. Fermann, B. J. Mintz, L. A. Burns, J. J. Wilke, M. L. Abrams, N. J. Russ, M. L. Leininger, C. L. Janssen, E. T. Seidl, W. D. Allen, H. F. Schaefer, R. A. King, E. F. Valeev, C. D. Sherrill, T. D. Crawford and J. M. Turney, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 556–565.
21. F. Neese, The ORCA program system, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 73–78.
22. S. F. Boys and F. Bernardi, Calculation of small molecular interactions by differences of separate total energies – some procedures with reduced errors, Mol. Phys., 1970, 19, 533–566.
23. W. Klopper, F. R. Manby, S. Ten-No and E. F. Valeev, R12 methods in explicitly correlated molecular electronic structure theory, Int. Rev. Phys. Chem., 2006, 25, 427–468.
24. H. J. Werner, T. B. Adler and F. R. Manby, Calculation of small molecular interactions by differences of separate total energies – some procedures with reduced errors, J. Chem. Phys., 2007, 126, 164102.
25. H. J. Werner, P. J. Knowles, G. Knizia, F. R. Manby and M. Schütz, Molpro: A general-purpose quantum chemistry program package, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 242–253.
26. T. L. Scott, M. M. Hashemi and M. S. Bratcher, Corannulene bowl-to-bowl inversion is rapid at room temperature, J. Am. Chem. Soc., 1992, 114, 1920–1921.
27. R. Pevarati and K. K. Baldridge, Implementation and performance of dft-d with respect to basis set and functional for study of dispersion interactions in nanoscale aromatic hydrocarbons, J. Chem. Theory Comput., 2008, 4, 2030–2048.
28. E. Białkowska-Jaworska, M. Jaworski and Z. Kisiel, The structure of cyclohexane, F-, Cl-, Br- and I-cyclohexane, J. Mol. Struct., 1995, 350, 247–254.
29. C. Brügger, H.-M. Frey, P. Steinegger, F. Balmer and S. Leutwyler, Accurate determination of the structure of cyclohexane by femtosecond rotational coherence spectroscopy and ab initio calculations, J. Phys. Chem. A, 2011, 115, 9567–9578.
30. Z. Kisiel, Least-squares mass-dependence molecular structures for selected weakly bound intermolecular clusters, J. Mol. Spectrosc., 2003, 218, 58–67.
31. Z. Kisiel, in Spectroscopy from Space, ed. Demaison J., et al., Assignment and analysis of complex rotational spectra, Kluwer Academic Publishers, 2001, pp. 91–106.
32. Z. Kisiel, PROSPE. Programs for RotationalSpectroscopy. URL http://info.ifpan.edu.pl/~kisiel/prospe.htm.
33. L. Hedberg, K. Hedberg, P.-C. Cheng and L. T. Scott, Gas-phase molecular structure of corannulene, C₂₀H₁₀. An electron-diffraction study augmented by ab initio and normal coordinate calculations, J. Phys. Chem. A, 2000, 104, 7689–7694.
34. C. H. Hanson and C. E. Nordman, The crystal and molecular structure of corannulene, C₂₀H₁₀, Acta Crystallogr., 1976, B32, 1147–1153.
35. S. Suzuki, P. G. Green, R. E. Bumgarner, S. Dasgupta, W. A. Goddard III and G. A. Blake, Benzene forms hydrogen bonds with water, Science, 1992, 257, 942–945.
36. H. S. Gutowsky, T. Emilsson and E. Arunan, Low-j rotational spectra, internal rotation, and structures of several benzene–water dimers, J. Chem. Phys., 1993, 99, 4883–4893.
37. G. T. Fraser, F. J. Lovas, F. D. Suenram, D. D. Nelson and W. Klemperer, Rotational spectrum and structure of CF₃H–NH₃, J. Chem. Phys., 1986, 84, 5983–5988.
38. S. E. Novick, P. Davies, S. J. Harris and W. Klemperer, Determination of the structure of ArHCl, J. Chem. Phys., 1973, 59, 2273–2279.
39. T. J. Balle, E. J. Campbell, M. R. Keenan and W. H. Flygare, A new method for observing the rotational spectra of weak molecular complexes, J. Chem. Phys., 1980, 72, 922–932.
40. W. G. Read, E. J. Campbell and G. Henderson, The rotational spectrum and molecular structure of the benzene-hydrogen chloride complex, J. Chem. Phys., 1983, 78, 3501–3508.
41. S. G. Kukolich and E. J. Campbell, Microwave measurements of bromine quadrupole coupling constants and the molecular structure of XeHBr, Chem. Phys. Lett., 1983, 94, 73–76.
42. A. Bondi, van der Waals Volumes and Radii, J. Phys. Chem., 1964, 68, 441–451.
43. F. C. D. De Lucia, P. Helminger and W. Gordy, Millimeter- and Submillimeter-Wavelength Spectrum and Molecular Constants of T₂O, Phys. Rev. A: At., Mol., Opt. Phys., 1973, 8, 2785–2791.
44. D. J. Millen, Determination of stretching force constants of weakly bound dimers from centrifugal distortion constants, Can. J. Chem., 1985, 7, 1477–1479.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c7cp01506b

---