Tracking areal lithium densities from neutron activation – quantitative Li determination in self-organized TiO₂ nanotube anode materials for Li-ion batteries

Abstract

Nanostructuring of electrode materials is a promising approach to enhance the performance of next-generation, high-energy density lithium (Li)-ion batteries. Various experimental and theoretical approaches allow for a detailed understanding of solid-state or surface-controlled reactions that occur in nanoscaled electrode materials. While most techniques which are suitable for nanomaterial investigations are restricted to analysis widths of the order of Å to some nm, they do not allow for characterization over the length scales of interest for electrode design, which is typically in the order of mm. In this work, three different self-organized anodic titania nanotube arrays, comprising as-grown amorphous titania nanotubes, carburized anatase titania nanotubes, and silicon coated carburized anatase titania nanotubes, have been synthesized and studied as model composite anodes for use in Li-ion batteries. Their 2D areal Li densities have been successfully reconstructed with a sub-millimeter spatial resolution over lateral electrode dimensions of 20 mm exploiting the ⁶Li(n,α)³H reaction, in spite of the extremely small areal Li densities (10–20 μg cm⁻² Li) in the nanotubular active material. While the average areal Li densities recorded via triton analysis are found to be in good agreement with the electrochemically measured charges during lithiation, triton analysis revealed, for certain nanotube arrays, areas with a significantly higher Li content (‘hot spots’) compared to the average. In summary, the presented technique is shown to be extremely well suited for analysis of the lithiation behavior of nanostructured electrode materials with very low Li concentrations. Furthermore, identification of lithiation anomalies is easily possible, which allows for fundamental studies and thus for further advancement of nanostructured Li-ion battery electrodes.

---

Introduction

The mobile world depends on Li-ion batteries which are considered to be today’s ultimate rechargeable energy storage. In particular, for small scale electronics, electrochemical energy storage through Li-ion batteries is the method of choice owing to their ability to provide high energy and sufficiently high power densities.^1–3 Furthermore, electrochemical energy storage in Li-ion batteries is expected to be the key technology for electrically powered vehicles, and is expected to substantially contribute to balancing the difference between supply and demand of renewable energy sources.⁴

However, most of the electrode materials in commercially available batteries are limited by low Li ion diffusion, slow electron transport and high resistances at the electrode/electrolyte interfaces, especially when charge and discharge are performed at high rates. In order to improve the cycling performance of batteries, various approaches have been implemented to develop materials with superior transport properties of electrons and of Li⁺ ions. In particular, different designs of nanomaterials and engineered nanostructures, such as nanowires, nanotubes, hollow spheres and porous nanostructures, with diminished pathways for Li⁺ ion transport have been successfully designed and shown to have stable cycling capacities and high rate capabilities.^5–10 Particularly, 1D structures have demonstrated outstanding performances as they provide a direct path for electron transport towards the current collector, and a high surface area for Li⁺-ion insertion, which is shortening the path for Li⁺ ion diffusion.¹¹ Significant attention has also been devoted to develop silicon coated nanostructures that can accommodate the lithiation-induced strain due to extreme volumetric and structural changes that occur during Li insertion/extraction into Si.

Among many other 1D-nanostructures, titanium dioxide (TiO₂) nanotubes (NT), which promise to provide important advantages in terms of cost-effectiveness, safety and environmental compatibility,^9,12 have been successfully applied for Li-ion insertion/extraction.^7,13,14 The simple way of nanostructuring by anodic oxidation of the parent Ti metal in fluoride containing electrolytes makes self-organized TiO₂ NT highly attractive as the anode material in Li-ion battery applications.¹⁴ Furthermore, no conductive binder is needed for the integration of the nanostructured electrodes in the cell, because the NT are grown on Ti metal which itself serves as a current collector. While this makes the system less complex and thus better suited for fundamental research than complex powder based electrodes, the low amount of the active electrode material, which is usually less than one mg per nanotube array, makes it almost impossible to accurately quantify the absolute Li-content in the electrode.

To further develop advanced macro-sized nanostructured anodes, such as self-organized TiO₂ NT arrays, it is essential to visualize and quantify the distribution of the inserted Li over macroscopic areas. Therefore, Li mapping over the millimeter length scales of interest for electrode design combined with sufficiently high spatial resolution is crucial. While in the literature potentially quantitative methods for Li detection, like X-ray diffraction (XRD),¹⁵ nuclear magnetic resonance spectroscopy (NMR)¹⁶ and X-ray photoelectron spectroscopy (XPS),¹⁷ are reported, these methods cannot be easily employed to obtain spatial information on the Li content.¹⁸ Other methods, like electron energy loss spectroscopy and transmission electron microscopy, can be used to image Li in a specimen volume of the order of Å to some nm,^19,20 which is suitable for the lattice structure analysis of active materials, but does not allow for Li mapping over the length scales of interest for electrode design.

We report on a quantitative 2D determination of the overall Li content in three different nanotubular anode arrays, comprising as-grown amorphous titania nanotubes (TiO₂ NT), carburized anatase titania nanotubes (TiO_2−x–C NT) and silicon-coated carburized anatase titania nanotubes (SiTiO_2−x–C NT) by triton analysis.²¹ The areal Li density in the nanotubular active material is extremely small (10–20 μg cm⁻² Li) compared to that in ink-based electrodes (0.1–10 mg cm⁻² Li), which renders its direct detection very challenging. This method allows for a non-destructive, position dependent, Li areal density measurement, with acceptable spatial resolution and very high sensitivity to Li over the full lateral electrode dimensions.

Results and discussion

Electrochemistry

For lithiation of nanotube arrays, a specially designed cell has been employed (Fig. S1a and b, ESI†) in order to avoid the use of a glass fiber separator between the anode and the Li metal counter electrode. Fig. S1a (ESI†) shows an exploded view of the lithiation cell with the position of the working electrode and the fully assembled cell. This cell design allows for non-destructive disassembly and recovery of the working electrodes after lithiation inside an Ar-filled glovebox.

The nanotubular electrodes are first lithiated by a galvanostatic process at a rate of C/10 from OCP to 1.1 V, followed by potentiostatic lithiation at 1.1 V until the lithiation current is no longer changing by more than 3 × 10⁻⁸ mA s⁻¹. This procedure leads, in the first approximation, to full lithiation of the TiO₂ NT. In this potential range, only TiO₂, not the Si coating, is lithiated. An example of the process is depicted in Fig. S1c (ESI†). The galvanostatic lithiation curve of anatase TiO_2−x–C NT can be described by three different regions: (i) a steady voltage decrease from 3 V to 1.73 V corresponding to the formation of the Li-poor anatase phase Li_xTiO₂ (0.01 < x ≤ 0.21)²² by diffusion of Li into the material, (ii) a plateau at 1.73 V corresponding to a phase transition from the tetragonal Li-poor anatase phase to orthorhombic lithium titanate Li_∼0.55TiO₂,^22–24 and (iii) a second, much smaller plateau at 1.43 V corresponding to a second phase transition to fully lithiated LiTiO₂. The theoretical capacity of fully lithiated LiTiO₂ is 335 mA h g⁻¹.^25,26 In the second step, the NT arrays are galvanostatically lithiated from OCP to 40 mV and potentiostatically until the lithiation current is no longer changing by more than 1 × 10⁻⁷ mA s⁻¹ (Fig. S4, ESI†). This procedure leads to lithiation of both TiO₂ and Si.

In the case of nanostructured electrodes in general, the uncertainties of the gravimetric capacities, induced by non-accurate determination of the active masses, are high. In the present case, uncertainties are induced by the nanoscopic dimensions of the nanotubes and the low amount of Si in the thin film coating, and by the high relative error of the morphological parameters. A detailed error analysis of this system for the determination of gravimetric capacities has been reported in ref. 7. Consequently, in the present work, areal capacities (in mA h cm⁻²) are chosen to represent the lithiation capacities because the error in area determination is as low as <2%, and the data can be directly compared to the reconstructed 2D areal Li density maps determined by triton analysis. Fig. S1d (ESI†) shows an optical image of the working electrode area, consisting of TiO_2−x–C NT on the supporting Ti-substrate with a diameter (∅) of 20.00 (±0.01) mm and a thickness (D) of 0.95 (±0.02) mm. For the calculation of the Li fraction x in Li_xTiO₂ however, the active electrode mass has to be taken into account.

Nanotube morphology, structure and chemical composition

Fig. 1 depicts scanning electron (SE) micrographs of amorphous TiO₂ NT, anatase TiO_2−x–C NT and Si coated SiTiO_2−x–C NT. The SEM images reveal 1.1 μm average tube length, 15 nm average wall thickness at the top, 115 nm average pore diameter, and a solid hemisphere at the bottom of each tube (Fig. S2, ESI†).

Fig. 1 SE micrographs of (a–c) TiO₂ NT, TiO_2−x–C NT and SiTiO_2−x–C NT after lithiation to 1.1 V and (d–f) the corresponding cross-sections.

Analysis of the SEM cross sections of the SiTiO_2−x–C NT reveals that the Si coating is about 10 nm thick and that it covers about 160 nm of the nanotube top length at both inside and outside walls (Fig. 1c, f and Fig. S2, ESI†). The mass of deposited Si was estimated to be ∼5 wt% of the SiTiO_2−x–C NT composite by calculating its volume fraction determined from the SE micrographs, a procedure already employed in ref. 7.

After carbothermal conversion at 400 °C and galvanostatic lithiation to 1.1 V, the NT are found to have an anatase structure. Ex situ XRD measurements in an argon atmosphere show the most prominent anatase peaks (101), (004), (200), (105) and (211) at 2θ ≈ 25, 38, 48, 54, and 55 for TiO_2−x–C NT (black) and SiTiO_2−x–C NT (blue), respectively (Fig. 2a). XRD reference measurements of the pristine samples before lithiation are shown in the ESI,† Fig. S3a. Intriguingly, for both TiO_2−x–C NT (black) and SiTiO_2−x–C NT (blue), after electrochemical lithiation to 1.1 V, no lithium-related new phase can be identified from the XRD spectra, and the original phases are well maintained, indicating that the lithiation process does not change the phase composition significantly. This is consistent with previous findings reported for similar systems.^13,27 A new peak at 35.9° is however observed for SiTiO_2−x–C NT (blue) that is not present in the pristine SiTiO_2−x–C NT (Fig. S3a, ESI†) and could not be clearly identified. In the case of the as-grown amorphous TiO₂ NT (red), only the Ti metal peaks are observed, with the most prominent peaks at ∼35° and 40°, corresponding to the (100) and (101) signals, because these nanotubes consist of amorphous TiO₂.¹⁴ Additionally, a peak at 43.7° is observed, which is only present in the lithiated, amorphous TiO₂ NT (red). This peak is very likely related to an electrochemically driven transformation of amorphous TiO₂ to a face-centered cubic crystalline phase,²⁸ as previously reported by Johnson and Rajh et al.²⁹

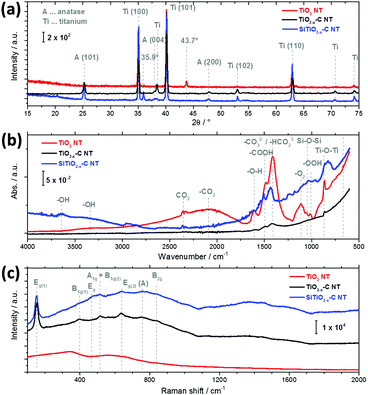Fig. 2 (a) XRD spectra, (b) ATR-FTIR spectra, and (c) micro-Raman spectra of TiO₂ NT (red), TiO_2−x–C NT (black) and SiTiO_2−x–C NT (blue) after lithiation to 1.1 V.

Ex situ ATR-FTIR spectra of the nanotubes before lithiation (Fig. S3b, ESI†) and after lithiation to 1.1 V (Fig. 2b) have also been recorded. In the case of pristine and lithiated NT arrays, a number of intense peaks that are found for amorphous TiO₂ NT (red) are not present in the case of the annealed TiO_2−x–C NT (black) and SiTiO_2−x–C NT (blue). The species on amorphous TiO₂ NT can be identified as adsorbed OH groups,^30–32 or can be attributed to adsorbed carbonate, carbon dioxide (CO₂) or COOH species, which are almost completely removed upon annealing, which is consistent with the literature.³³ The vibrations in the region around 3375 cm⁻¹ are characteristic of the hydroxyl groups from Ti–OH where weak hydrogen bonds are formed with the TiO₂ surface.^32,34 The relatively broad peak at 2100 cm⁻¹ can be assigned to weakly adsorbed CO₂,³⁵ while the double peak centered around 2350 cm⁻¹ is due to atmospheric CO₂ that could not be totally removed during the measurements. The signal at 1630 cm⁻¹ is associated with the deformation vibration of –O–H from physisorbed water.³² The absorption band at 1480 cm⁻¹ belongs to the symmetric and asymmetric stretching vibrations of carboxylate groups.³⁶ The band at 1415 cm⁻¹ is related to antisymmetric stretching modes of CO₃²⁻ and HCO₂³⁻ ions and is found to strongly increase for TiO₂ NT (red) upon lithiation (compare Fig. S3b, ESI†).^32,37,38 The Ti–O stretching mode is observed at 837 cm⁻¹.³¹ The FT-IR spectrum of TiO_2−x–C NT shows no signal other than the double peak of atmospheric CO₂ and small features at 1415 cm⁻¹ (CO₃²⁻ and HCO₂³⁻) and 837 cm⁻¹ (Ti–O stretching). In the spectrum of SiTiO_2−x–C NT, a number of very small features can be identified in addition to the double peak of atmospheric CO₂, i.e., at 3630 cm⁻¹ (unsymmetrical stretching of water molecules),³³ ∼3300 cm⁻¹ (Ti–OH stretching), 2100 cm⁻¹ (–CO₂) and ∼1500 cm⁻¹ (–COOH). The small peak at 1045 cm⁻¹, which is also present in the reference spectra of SiTiO_2−x–C NT (Fig. S3b, ESI†), is indicative of Si–O–Si.^39,40

The crystalline phases of as-grown TiO₂ NT, TiO_2−x–C NT and SiTiO_2−x–C NT before lithiation (Fig. S3c, ESI†) and after lithiation to 1.1 V (Fig. 2c) have been further investigated using Raman spectroscopy. After lithiation, no distinct Raman signals are measured in the case of amorphous TiO₂ NT (red). Four main Raman peaks are observed for TiO_2−x–C NT (black) and SiTiO_2−x–C NT (blue) at 145, 399, 516, and 634 cm⁻¹ that can be ascribed to the E_g, B_1g (1), A_1g/B_1g (2), and E_g (2) vibration modes of the anatase phase for pure TiO₂.^41,42 The weak features between 700 and 800 cm⁻¹ may be attributed to the combination bands of anatase TiO₂ (indicated by (A)),⁴³ while the peaks detected at ∼460 cm⁻¹ (only in the spectrum of SiTiO_2−x–C NT) and at 826 cm⁻¹ can be assigned to the E_g and B_2g bands of rutile TiO₂.⁴⁴ In the presence of anatase TiO₂, the small B_1g band of rutile at 143 cm⁻¹ is usually obscured due to its proximity to the anatase E_g band. However, there is also no distinct peak visible at 612 cm⁻¹ that is caused by the Raman active A_1g mode of rutile, suggesting a very low fraction of the rutile phase compared to the anatase phase in TiO₂.^43,45 In line with the XRD results (Fig. 2a), no lithium-related new phase can be identified from the micro-Raman spectra after electrochemical lithiation to 1.1 V compared to the pristine samples before lithiation (Fig. S3c, ESI†). However, the band maximum position of the anatase E_g mode slightly shifts from 639 to 634 cm⁻¹, which is consistent with previous findings reported for similar systems.⁴⁶ Furthermore, the Raman spectra of TiO_2−x–C NT and SiTiO_2−x–C NT show two weakly resolved bands at 1352 and 1457 cm⁻¹ that may originate from amorphous carbon⁴⁷ and adsorbed polyenes present on TiO₂ after acetylene treatment at 400 °C.^41,42 It has been shown earlier that this carbon in TiO_2−x–C NT and SiTiO_2−x–C NT originates from carburization treatment during nanotube preparation.¹⁴ The band at 1125 cm⁻¹ (SiTiO_2−x–C NT) is attributed to the asymmetric stretching vibration of Ti–O–Si.^48,49

Triton analysis

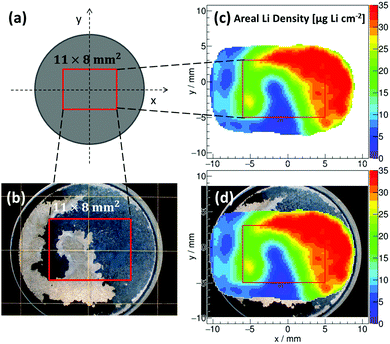
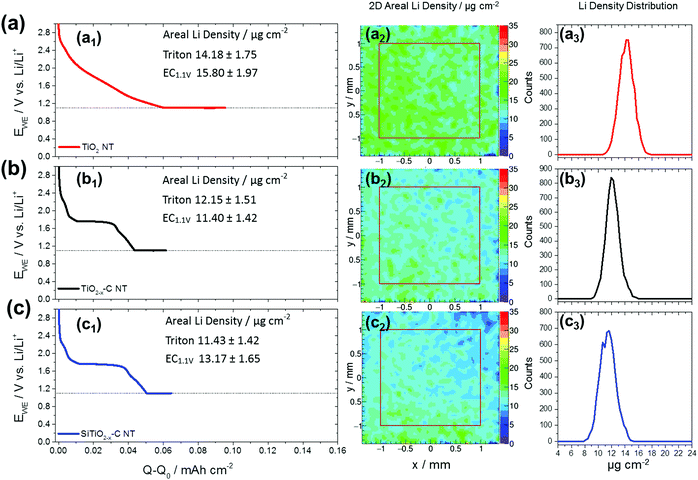
Tritons from the ⁶Li(n,α)³H reaction are measured using a position-sensitive silicon detector having a spatial resolution of 300 μm. Local count rates are used to determine the areal Li concentrations in TiO₂ NT, TiO_2−x–C NT and SiTiO_2−x–C NT on Ti-substrates with diameters of 20.00 (±0.01 mm), Ti substrate thicknesses of 0.95 (±0.02 mm) (Fig. S1d, ESI†), and thicknesses of the nanotubular active materials of ∼1 μm (Fig. 1). In Fig. 3, an example of a reconstructed 2D areal Li density of lithiated TiO_2−x–C NT is shown, where the nanotube array has been partially peeled off upon rinsing with DMC after the electrochemical lithiation process. The reconstructed areal Li density (Fig. 3c) is compared to an optical microscopy image of the same electrode (Fig. 3b). Fig. 3d shows an overlay of both graphs; the electrode areas fully covered with lithiated NT are shown in black and red, respectively. Areas where the nanotube film has been removed are shown in beige and blue, the transition states also coincide in both pictures. For this partially removed lithiated TiO_2−x–C NT array, it is clearly visible that the reconstructed 2D areal Li density from triton analysis exactly resembles the area that is still covered with NT. This is a proof of principle for the applicability of the method to Li detection in self-organized TiO₂ NT electrodes.

Fig. 3 Proof of principle: triton analysis on a partially removed lithiated TiO_2−x–C NT array: (a) scheme of the electrode surface area and the analyzed area reduced to 11 × 8 mm² (red cut), (b) optical micrograph of the electrode surface with the analyzed area (red cut), (c) reconstructed areal Li density on the 11 × 8 mm² target region (red cut), (d) position dependent areal Li density in μg cm⁻² super-imposed over the microscopy image.

Fig. 4 shows galvanostatic lithiation to 1.1 V (C/10), followed by potentiostatic lithiation at 1.1 V of (a₁) TiO₂ NT, (b₁) TiO_2−x–C NT, and (c₁) SiTiO_2−x–C NT, the corresponding reconstructed areal Li densities on a 2 × 2 mm² area in μg cm⁻² (Fig. 4a₂–c₂), and areal Li density distributions over the analyzed area in Fig. 4a₃–c₃. The as-grown amorphous TiO₂ NT show a steady voltage decrease within the given potential range from 3.0 to 1.1 V. In the case of the TiO_2−x–C NT, the plateau that indicates the phase transition from Li-poor anatase TiO₂ to Li-titanate ends at 31 μA h cm⁻² (Li_0.33TiO₂), which indicates that not all of the active mass is undergoing the first phase transition to Li_0.55TiO₂ under the applied lithiation conditions.

Fig. 4 Galvanostatic lithiation to 1.1 V (C/10), followed by potentiostatic lithiation at 1.1 V of (a₁) TiO₂ NT, (b₁) TiO_2−x–C NT, and (c₁) SiTiO_2−x–C NT, (a₂–c₂) the corresponding reconstructed areal Li densities in μg cm⁻² reduced to 2 × 2 mm² and (a₃–c₃) areal Li density distributions in μg cm⁻² over the analyzed area.

For SiTiO_2−x–C NT, the same plateau ends at 38 μA h cm⁻² (Li₄₁TiO₂). The lithiation behavior to 1.1 V of TiO_2−x–C NT and SiTiO_2−x–C NT is similar since Li insertion into Si starts at ∼0.25 V.⁷ A relatively homogeneous lithiation behavior over the analyzed surface area is observed in all three cases. For TiO₂ NT, the areal capacity for galvanostatic lithiation to 1.1 V is determined to be 61 μA h cm⁻² and the areal Li density does not show remarkable changes over the analyzed surface area with an average value of 14.2 μg cm⁻² determined from triton detection (Fig. 4a₁–a₃).

The areal capacities of TiO_2−x–C NT for galvanostatic lithiation to 1.1 V are determined to be 44 μA h cm⁻² (Fig. 4b₁) and for SiTiO_2−x–C NT with 50 μA h cm⁻² (Fig. 4c₁). Both electrochemistry (EC) and triton analysis reveal the highest Li areal density for the amorphous TiO₂ NT with 15.8 (±1.9) μg_Li cm⁻² measured electrochemically and 14.2 (±1.8) μg_Li cm⁻² from triton analysis. The Li content detected for anatase TiO_2−x–C NT is 11.4 (±1.4) and 12.1 (±1.5) μg_Li cm⁻² and that for SiTiO_2−x–C NT 13.2 (±1.7) and 11.4 (±1.4) μg_Li cm⁻² from electrochemistry and triton analysis, respectively. These results are in agreement with the literature, where in general amorphous TiO₂ nanoparticles are shown to reveal higher capacities, especially on the first discharge, compared to anatase nanoparticles.³⁰ The Li content measured electrochemically is typically higher than the corresponding value recorded via triton analysis. This can be explained by surface lithiation and subsequent removal of Li containing species during electrode emersion and rinsing, and/or through side reactions taking place during the electrochemical lithiation process. Electrochemistry and triton analysis reveal much higher Li contents for all three materials after lithiation to 0.04 V compared to lithiation to 1.10 V (Fig. S4, ESI†). The contribution of Si is visualized through a comparison between TiO_2−x–C NT and SiTiO_2−x–C NT (Fig. S5, ESI†). After galvanostatic lithiation to 0.04 V, the gravimetric capacity of the SiTiO_2−x–C NT composite is determined to be 462 (±114) mA h g⁻¹, whereas that of TiO_2−x–C is 332 (±82) mA h g⁻¹, yielding a gravimetric capacity of 2671 (±662) mA h g⁻¹ for Si alone. These results are comparable to previous findings reported for a similar system.⁷ A summary of the average Li surface densities for all three materials measured via triton analysis and EC and their corresponding error estimations is provided in Table 1. The differences between the results obtained via triton analysis and EC in the case of amorphous TiO₂ NT are 1.62 μg_Li cm⁻² when lithiated to 1.1 V and 6.72 μg_Li cm⁻² when lithiated to 0.04 V. For lithiation to 1.1 V, the areal Li densities obtained from both methods are comparable, given the uncertainties in the measurements of ±1.75 μg_Li cm⁻² (trition analysis) and ±1.97 μg_Li cm⁻² (EC). For anatase TiO_2−x–C NT the differences between triton analysis and EC are 0.75 μg_Li cm⁻² when lithiated to 1.1 V and 6.46 μg_Li cm⁻² when lithiated to 0.04 V. For SiTiO_2−x–C NT the variation is 1.74 μg_Li cm⁻² when lithiated to 1.1 V and 12.83 μg_Li cm⁻² when lithiated to 0.04 V. In summary, Table 1 shows that in most cases the average areal Li densities determined via EC and triton analysis are quite similar. The absolute differences are sometimes within the given range of errors when the NT are lithiated to 1.1 V. For all NT arrays a surplus of Li is measured electrochemically, except for TiO_2−x–C NT lithiated to 1.1 V. In this measurement however, the absolute difference (0.75 μg_Li cm⁻²) is within the given error (±1.51 μg_Li cm⁻²).

Table 1 Average areal Li density in μg cm⁻² from triton analysis and from electrochemistry (EC) and their corresponding error estimations

Structure/sample	Lithiation potential [Vvs. Li/Li^+]	Areal Li density – triton [μgLi cm^−2]	Error [μgLi cm^−2]	Areal Li density – EC [μgLi cm^−2]	Error [μgLi cm^−2]	Areal Li density difference [μgLi cm^−2]	x in LixTiO2^a
a Mole Li per mole TiO2, calculated from the areal Li density measured by triton analysis and using the average 24.4 μgLi cm^−2 as x = 1.
TiO2 NT	1.10	14.18	±1.75	15.80	±1.97	1.62	0.58
TiO2 NT	0.04	24.18	±2.96	30.90	±3.86	6.72	0.99
TiO2−x–C NT	1.10	12.15	±1.51	11.40	±1.42	0.75	0.50
TiO2−x–C NT	0.04	22.98	±2.82	29.44	±3.68	6.46	0.94
SiTiO2−x–C NT	1.10	11.43	±1.42	13.17	±1.65	1.74	0.47
SiTiO2−x–C NT	0.04	23.66	±2.90	36.49	±4.56	12.83	0.97

---

The electrochemically measured Li excess, especially when lithiated to low potentials (i.e. 0.04 V), can be explained by a loss of unreacted Li through electrode emersion and rinsing prior to triton analysis. The highest variance (12.83 μg_Li cm⁻²) is observed for SiTiO_2−x–C NT when lithiated to 0.04 V, where the high Li amount measured electrochemically might originate from surface reactions on SiO₂ that are absent on TiO_2−x–C NT.

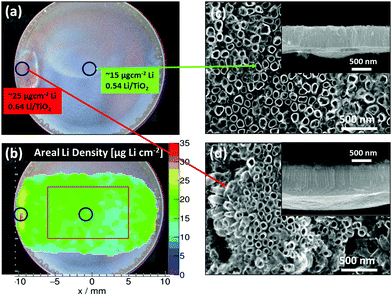
Due to inhomogeneities of the nanostructured electrodes, the areal Li density is prone to lateral variations when measured macroscopically. This is most likely the reason for the observed variations in lithiation/delithiation performance for identically prepared electrode materials, which have been especially noticeable in the case of anatase TiO₂ NT.¹³ In Fig. 5, the TiO_2−x–C NT array, the central position of which has been probed to determine the areal Li density depicted in Fig. 4b, is examined over its complete width. In contrast to the homogeneous Li distribution in the center, the areal Li density of the anatase TiO_2−x–C NT depicts a ‘hot-spot’, i.e., an area with a significantly higher Li content compared to the average, at the rim of the array (Fig. 5b). While the corresponding lithiation curve does not indicate any special feature (Fig. 4b₁), SEM analysis after lithiation reveals the presence of nanotubes with an increased length of 1.7 (±0.1) μm (Fig. 5d) compared to an average of 1.1 (±0.1) μm (Fig. 5c) at the spot where a higher Li density is detected.

Fig. 5 Example of inhomogeneous areal Li density: (a) optical micrograph of the TiO₂–C NT electrode, with indicated areas for SEM analysis (blue circles) and the corresponding areal Li densities in μg cm⁻² highlighted in the red and green textbox, and (b) position dependent areal Li density in μg cm⁻² overlaid with the micrograph. The red cut shows the area used to determine the average Li content. SEM images (c) and (d) show details of TiO_2−x–C NT after lithiation for standard areas (green) and ‘hot spots’ (red). Insets: Cross sections of the TiO_2−x–C NT.

When this increased length is taken into account, the degree of lithiation at the hot spot, with ∼0.64 (±0.20) mole Li per mole TiO₂, is comparable to the average Li density of ∼0.54 (±0.10) mole Li per mole TiO₂. The nature of this ‘hot spot’ may be attributed to an edge effect which can occur in the vicinity of the O-ring during anodization and which results in an increased nanotube length.

However, inhomogeneous lithiation behavior cannot always be explained by an increased amount of active material caused by morphological inhomogeneities. Fig. 6 shows a second example where inhomogeneous lithiation behaviour is observed using triton analysis of the Li concentration in SiTiO_2−x–C NT after lithiation to 1.1 V. In a ‘hot spot’ of about 11 mm length and 5 mm width, the Li areal density reaches values as high as 25 μg cm⁻², while the average Li areal density is 15 μg cm⁻². Investigation of the electrode morphology in the areas of interest reveals that the average nanotube lengths (950 (±100) nm) and outer diameters (135 (±20) nm) are identical for regions with high and average Li concentrations (Fig. 6b and c). In Fig. 6d, a lithiation curve of optimally performing anatase TiO_2−x–C NT¹³ is depicted, showing the first and second phase transition to Li_0.55TiO₂ and to fully lithiated LiTiO₂. The formation of LiTiO₂ is indicated by a small plateau at ∼1.50 V (Fig. 6d). The x-axis has been translated to the molar fraction x in Li_xTiO₂ and the different lithiation stages are emphasized by different background colors, which are in accordance with the corresponding phase transitions in the lithiation curve.

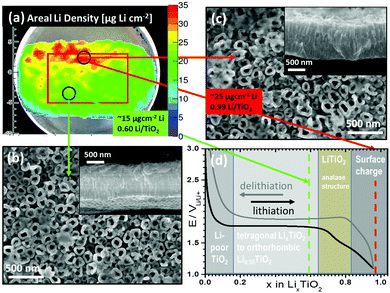Fig. 6 Example of inhomogeneous areal Li density in SiTiO_2−x–C NT: (a) position dependent areal Li density in μg cm⁻² super-imposed with the micrograph, (b) and (c) SEM images of SiTiO_2−x–C NT after lithiation to 1.1 V for areas with an average Li content (green) and ‘hot spots’ (red). Insets: Cross sections. (d) Example for optimal EC lithiation of TiO_2−x–C NT,¹³ showing the potential over the molar fraction x in Li_xTiO₂ and the different lithiation stages emphasized by different background colors, which are in accordance with the corresponding phase transitions in the lithiation curve. The corresponding molar fractions of the hot spots and areas with average Li content are indicated by red and green dashed lines.

The corresponding molar fractions at the points of analysis for high (∼25 μg_Li cm⁻², Li_0.99TiO₂) and medium (15 μg_Li cm⁻², Li_0.60TiO₂) Li content are depicted as vertical dashed lines. For the areas where an average Li content (green) is measured, lithiation of SiTiO_2−x–C NT leads to the formation of Li_0.60TiO₂ (∼15 μg_Li cm⁻²). The areas of high Li content (red), with ∼25 μg_Li cm⁻², indicate full lithiation of the NT to LiTiO₂ and may indicate Li storage at the surface of the material. In this context, it is important to note that triton analysis does not distinguish Li intercalated in the nanotube bulk and Li that is adsorbed at the surface. In order to analyze the nature of adsorbates on the surfaces of SiTiO_2−x–C NT at the positions of high and medium Li concentration, local ATR-FTIR and micro-Raman analysis have been conducted. Both methods do not show any significant difference between areas with high and medium Li content. The amount of adsorbates is lower than that detected on amorphous TiO₂ NT (Fig. S6, ESI†). Therefore, the origin of the high areal Li density at the ‘hot spot’ does not seem to be related to surface lithiation, as sometimes reported to explain exceptionally the high Li content in amorphous TiO₂ electrodes.^30,50 It can thus be assumed that the observed ‘hot spot’ is rather explainable through a bulk phenomenon, possibly due to the kinetic effects during nanotube lithiation.^51–53 It can be assumed that at the positions where ‘hot spots’ are detected via triton analysis, the lithiation kinetics are faster. This could be due to a different texture of the NT at that particular position, which in turn can be caused by inhomogeneities in the local fluoride and water concentrations during nanotube growth. Another reason for the different Li concentrations could be the presence of adsorbates, as for example LiF, which is nonabsorbing in the mid-IR region (∼600–4000 cm⁻¹).⁵⁴ However, LiF should show defined Raman peaks at 288, 470 and 659 cm⁻¹ for E_g, A_1g and T_2g modes,⁵⁵ which we should have detected.

Further endeavors to fundamentally understand these inhomogeneous areal Li densities of TiO_2−x–C NT and SiTiO_2−x–C NT are ongoing in our group.

Conclusions

In conclusion, three different electrode compositions, comprising as-grown amorphous titania nanotubes (TiO₂ NT), carburized anatase titania nanotubes (TiO_2−x–C NT) and silicon-coated carburized anatase titania nanotubes (SiTiO_2−x–C NT), have been synthesized and investigated in terms of their lithiation behavior. The 2D areal Li densities have been reconstructed with a new position sensitive triton analysis technique. The results have been compared to electrochemical lithiation measurements. In general, the average Li areal density determined by both methods is found to be quite similar. In particular, for anatase TiO_2−x–C NT, the differences between triton analysis and EC (0.75 μg_Li cm⁻²), when lithiated to 1.1 V, is within the given range of errors (±1.51 μg_Li cm⁻²). The highest difference between both methods is observed for SiTiO_2−x–C NT after lithiation to 0.04 V, where the electrochemically measured Li excess may be explained by surface lithiation reactions taking place on SiO₂ and removal of Li upon emersion. For certain nanotube arrays, triton analysis reveals areas with a significantly higher Li content compared to the average (‘hot spots’). In some cases, the locally higher Li content is explained by the locally confined presence of NT with increased length. Other ‘hot spots’, however, are not yet fully understood and may originate from inhomogeneities in the local fluoride and water concentrations during nanotube growth, resulting in different textures of the nanotubes that can cause differences in the bulk lithiation kinetics or differences in the occurrence of Li containing adsorbates not detectable with the analysis techniques used in this paper. While this is subject to further studies, the straightforward and simultaneous identification of such local heterogeneities in lithiation characteristics, together with the possibility to detect relatively small Li densities (<10 μg Li cm⁻²), on a considerably large electrode area, is essential for an efficient analysis of the performance of the nanostructured electrode. This type of local Li density determination therefore allows us to control large-area changes due to solid-state or surface-controlled reactions, when using Li as the active element, however it does not allow for discrimination between Li inserted in the bulk of the active material and surface Li. The insights obtained from triton analysis will therefore provide guidance for designing optimized nanostructured Li-battery electrodes.

Experimental

Nanotube synthesis and Si deposition

TiO₂ NT were grown electrochemically on mechanically polished (4000P SiC grinding paper) Ti disks (99.6%, Advent) by exposing the polished surface (2.54 cm²) to an electrolyte containing 50% ethylene glycol by volume (99.5%, Merck) in water (18.2 MU cm, Milli-Q, Millipore) and 1 wt% NH₄F (99.99%, Merck), and by applying an anodic potential of 20 V for 1 h, after a voltage ramp of 1 V s⁻¹. After anodization, the sample was thoroughly rinsed with deionized water to prevent further etching of the surface. In order to increase the electronic conductivity and to modify the Li insertion properties of the as-grown amorphous TiO₂ NT, carbothermal annealing was carried out in a horizontal tube furnace. The reactor tube was first purged with 750 sccm Ar for 2 h at room temperature (RT) to remove air. The Ar flow was then reduced to 200 sccm and kept constant until the end of the annealing procedure. Prior to increasing the temperature, 5 sccm acetylene were added to the Ar flow for 3 min. To avoid thermal stress during the temperature increase to 400 °C, the ramping speed was gradually reduced from 10 °C min⁻¹ until 200 °C, to 5 °C min⁻¹ until 300 °C, and finally 3 °C min⁻¹ until 400 °C. After 20 min at 400 °C, 0.1 sccm acetylene was added to the Ar flow for 1 h. The system was then kept for another 280 min at 400 °C to allow for the complete transformation of the NT and then cooled down to RT at 3 °C min⁻¹. PECVD (Oxford Plasmalab 80þ) with Ar diluted SiH₄ was used to coat the annealed NT with silicon, at 1 Torr total pressure, with 465 sccm Ar and 35 sccm SiH₄ at 250 °C for 1 min.

Electrochemistry

The electrolyte (SelectiLyte battery electrolyte LP 30, Merck) used in all measurements was 1 mole LiPF₆ in a 1 : 1 (w/w) mixture of ethylene carbonate (EC) and dimethyl carbonate (DMC) with or without a 2 wt% vinylene carbonate (VC) additive.⁵⁶ All potentials herein provided are with respect to the Li/Li⁺ reference electrode unless stated otherwise. All cells were assembled in an Ar-filled glove box with water and oxygen contents below 0.1 ppm. The assembled cells were connected to a potentiostat (BioLogic VSP) outside the glove box, and all measurements were performed at room temperature. Galvanostatic lithiation with potential limitation was carried out in the potential window from 0.04 to 3.0 V vs. Li/Li⁺ at a constant current of j₀/10 = 6.7 μA cm⁻² corresponding to a lithiation rate of approx. 0.07C, where the C-rate of 1C = 96 μA cm⁻² is derived from the maximal theoretical capacity of 96 μA h cm⁻². Error estimations regarding the calculation of the volume and mass of the active electrode were done by applying the Gaussian error propagation with independent parameters.

For transfer of the lithiated samples to the PGAA experiment, an airtight target box has been used (Fig. S7, ESI†) to avoid contact with the ambient atmosphere.

Spectroscopic, diffractometric and microscopic characterization

Scanning electron microscopy (SEM) images (using the CrossBeam NVision 40, Zeiss spectrometer), were used to determine the active electrode TiO₂ volume and corresponding mass fraction of deposited Si. Micrographs were recorded for TiO₂ NT, TiO_2−x–C NT and SiTiO_2−x–C NT before and after Si deposition. The micrographs were acquired with an electron acceleration voltage of 15 kV using the inlens detector. Structural and compositional information about the NT films was obtained by X-ray diffraction (XRD). The XRD analysis was performed on a Siemens D5000 diffractometer. Diffractograms were acquired between 15 and 75 degrees (2 theta) with a step size of 0.02 degrees (2 theta) and an acquisition time of 1 s per step in an argon atmosphere. Additional ATR-FTIR (Nicolet iS5) and micro-Raman spectra of SiTiO_2−x–C NT were used for surface and structural characterization. ATR-FTIR absorption spectra were recorded in the −ΔT/T mode with a spectral resolution of 4 cm⁻¹, using a polished Ti-disk as a reference sample. An Olympus BX40 micro-Raman instrument equipped with a He/Ne laser (632.8 nm) was used in a non-focal operation mode and without a polarizer to analyze the average chemical composition and structure of the films for the micro-Raman spectra. The size of the focused laser spot on the sample was determined to be about 1 mm using 50× magnification of the optical microscope. Back-scattered Raman signals were recorded with a resolution of less than 2 cm⁻¹ (as determined by measuring the Rayleigh line) in a spectral range from 90 to 2000 cm⁻¹.

Triton analysis

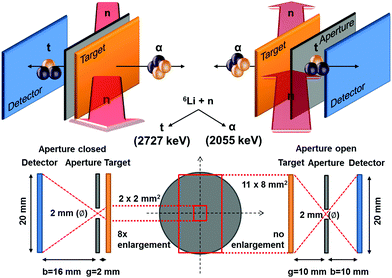
The method is based on the neutron capture reaction ⁶Li(n,α)³H. ⁶Li occurs in natural Li with an isotopic abundance of 7.42%,⁵⁷ and has a large thermal neutron capture cross section σ_th = 940 ± 4.⁵⁸ In the case of neutron capture, the compound nucleus immediately decays into an alpha (α) and a tritium (t) particle (triton) which, in the laboratory system, are emitted in opposite directions due to momentum conservation.

Because of the reaction Q value, the α and the t particles obtain a fixed and relatively high kinetic energy of E_α = 2055 keV and E_t = 2727 keV, respectively.⁵⁹ The basic concept of the detection method is schematically depicted in Fig. 7. A position sensitive silicon detector (Fig. S8, ESI†) is facing the target which is irradiated by cold neutrons where the cross section σ_c = 3474 barn is about 3.6 times larger than in the case of thermal neutrons. Both alpha particles and tritons emitted in the Li capture reaction are detected alternatively (Fig. S9, ESI†). A pinhole aperture at different distances between the target and the detector is used for imaging. The detector as well as the target are tilted by θ = 25° with respect to the axis of the neutron beam.⁶⁰ For quantitative analysis, the spectrum of a Li reference sample coated by vapor deposition with a well-defined amount of Li (λ_ref = 50 μg LiF_nat cm⁻²) has been used.

Fig. 7 Scheme of the PGAA experiment. Upon neutron absorption ⁶Li decays into one α (E_kin = 2055 keV) and one tritium (E_kin = 2727 keV) particle. The measurements were performed in compact (left) and open (right) geometry. The compact geometry allowed for 8× enlargement but a low area of analysis (2 × 2 mm²) and the open aperture geometry allowed no enlargement but a larger area of analysis (11 × 8 mm², drawing not true to scale).

Acknowledgements

We thank the research neutron source Heinz Maier-Leibnitz (MLZ) for providing beamtime and support at the instrument. J. K.-L. and E. P. thank the DFG (project KU 2397/3-1) and the Austrian Science Foundation (FWF, project P235675) for financial support. Financial support from the DFG project (GE 2296/1-1) and (BMBF 05K16WO1) is gratefully acknowledged by R. G. and G. N.

References

1. M. Armand and J.-M. Tarascon, Nature, 2008, 451, 652–657.
2. B. Scrosati and J. Garche, J. Power Sources, 2010, 195, 2419–2430.
3. R. Van Noorden, Nature, 2014, 507, 26–28.
4. X. Zhang, M. van Hulzen, D. P. Singh, A. Brownrigg, J. P. Wright, N. H. van Dijk and M. Wagemaker, Nat. Commun., 2015, 6, 8333.
5. A. A. Belak, Y. Wang and A. Van der Ven, Chem. Mater., 2012, 24, 2894–2898.
6. M. T. McDowell, S. W. Lee, W. D. Nix and Y. Cui, Adv. Mater., 2013, 25, 4966–4985.
7. J. Brumbarov and J. Kunze-Liebhäuser, J. Power Sources, 2014, 258, 129–133.
8. N. Liu, Z. Lu, J. Zhao, M. T. McDowell, H.-W. Lee, W. Zhao and Y. Cui, Nat. Nanotechnol., 2014, 9, 187–192.
9. S. Goriparti, E. Miele, F. De Angelis, E. Di Fabrizio, R. Proietti Zaccaria and C. Capiglia, J. Power Sources, 2014, 257, 421–443.
10. P. Acevedo-Peña, M. Haro, M. E. Rincón, J. Bisquert and G. Garcia-Belmonte, J. Power Sources, 2014, 268, 397–403.
11. S. Ding, J. S. Chen and X. W. David Lou, Adv. Funct. Mater., 2011, 21, 4120–4125.
12. Z. Li, J. Huang, B. Yann Liaw, V. Metzler and J. Zhang, J. Power Sources, 2014, 254, 168–182.
13. J. Brumbarov, J. P. Vivek, S. Leonardi, C. Valero-Vidal, E. Portenkirchner and J. Kunze-Liebhäuser, J. Mater. Chem. A, 2015, 3, 16469–16477.
14. K. Lee, A. Mazare and P. Schmuki, Chem. Rev., 2014, 114, 9385–9454.
15. I. Buchberger, S. Seidlmayer, A. Pokharel, M. Piana, J. Hattendorff, P. Kudejova, R. Gilles and H. A. Gasteiger, J. Electrochem. Soc., 2015, 162, A2737–A2746.
16. M. Wagemaker, A. P. M. Kentgens and F. M. Mulder, Nature, 2002, 418, 397–399.
17. S. Brutti, V. Gentili, H. Menard, B. Scrosati and P. G. Bruce, Adv. Energy Mater., 2012, 2, 322–327.
18. S. K. Aghara, S. Venkatraman, A. Manthiram and E. Alvarez, J. Radioanal. Nucl. Chem., 2005, 265, 321–328.
19. F. Wang, J. Graetz, M. S. Moreno, C. Ma, L. Wu, V. Volkov and Y. Zhu, ACS Nano, 2011, 5, 1190–1197.
20. D. Santhanagopalan, D. Qian, T. McGilvray, Z. Wang, F. Wang, F. Camino, J. Graetz, N. Dudney and Y. S. Meng, J. Phys. Chem. Lett., 2014, 5, 298–303.
21. Y. He, R. G. Downing and H. Wang, J. Power Sources, 2015, 287, 226–230.
22. M. Wagemaker, W. J. H. Borghols and F. M. Mulder, J. Am. Chem. Soc., 2007, 129, 4323–4327.
23. B. Zachau-Christiansen, Solid State Ionics, 1988, 28–30, 1176–1182.
24. L. Kavan, M. Grätzel, S. E. Gilbert, C. Klemenz and H. J. Scheel, J. Am. Chem. Soc., 1996, 118, 6716–6723.
25. M. Wagemaker, W. J. H. Borghols and F. M. Mulder, J. Am. Chem. Soc., 2007, 129, 4323–4327.
26. W. J. H. Borghols, D. Lützenkirchen-Hecht, U. Haake, E. R. H. van Eck, F. M. Mulder and M. Wagemaker, Phys. Chem. Chem. Phys., 2009, 11, 3010.
27. D. Wang, L. Liu, X. Sun and T.-K. Sham, J. Mater. Chem. A, 2015, 3, 412–419.
28. A. Laumann, K. T. Fehr, H. Boysen, M. Hölzel and M. Holzapfel, Z. Kristallogr., 2011, 226, 53–61.
29. H. Xiong, H. Yildirim, E. V Shevchenko, V. B. Prakapenka, B. Koo, M. D. Slater, M. Balasubramanian, S. K. R. S. Sankaranarayanan, P. Greeley, S. Tepavcevic, N. M. Dimitrijevic, P. Podsiadlo, C. S. Johnson and T. Rajh, J. Phys. Chem. C, 2012, 116, 3181–3187.
30. W. J. H. Borghols, D. Lützenkirchen-Hecht, U. Haake, W. Chan, U. Lafont, E. M. Kelder, E. R. H. van Eck, A. P. M. Kentgens, F. M. Mulder and M. Wagemaker, J. Electrochem. Soc., 2010, 157, A582.
31. M. Wan, W. Li, Y. Long and Y. Tu, Anal. Methods, 2012, 4, 2860.
32. G. Li, L. Li, J. Boerio-Goates and B. F. Woodfield, J. Am. Chem. Soc., 2005, 127, 8659–8666.
33. S. Liu, W. Wang, J. Chen, J.-G. Li, X. Li, X. Sun and Y. Dong, J. Mater. Chem. A, 2015, 3, 17837–17848.
34. T. Bezrodna, G. Puchkovska, V. Shimanovska, I. Chashechnikova, T. Khalyavka and J. Baran, Appl. Surf. Sci., 2003, 214, 222–231.
35. Q. Chen, H. Liu, Y. Xin and X. Cheng, Electrochim. Acta, 2013, 111, 284–291.
36. E. Filippo, C. Carlucci, A. L. Capodilupo, P. Perulli, F. Conciauro, G. A. Corrente, G. Gigli and G. Ciccarella, Mater. Res., 2015, 18, 473–481.
37. X. Li, H. Liu, J. Wang, H. Cui, X. Zhang and F. Han, Mater. Sci. Eng., A, 2004, 379, 347–350.
38. J. T. Kloprogge, D. Wharton, L. Hickey and R. L. Frost, Am. Mineral., 2002, 87, 623–629.
39. P. Yang, Q. Tang and B. He, RSC Adv., 2015, 5, 46260–46266.
40. Y. Li, X. Ge, X. Pang, X. Yu, X. Zhen, L. Geng and Y. Wang, Mater. Lett., 2015, 152, 170–172.
41. C. Rüdiger, M. Favaro, C. Valero-Vidal, L. Calvillo, N. Bozzolo, S. Jacomet, C. Hejny, L. Gregoratti, M. Amati, S. Agnoli, G. Granozzi and J. Kunze-Liebhäuser, Phys. Chem. Chem. Phys., 2016, 18, 9220–9231.
42. S. Xiao, W. Zhu, P. Liu, F. Liu, W. Dai, D. Zhang, W. Chen and H. Li, Nanoscale, 2016, 8, 2899–2907.
43. J. Tang and H. M. Meng, Phys. Chem. Chem. Phys., 2016, 18, 1500–1506.
44. S. P. S. Porto, P. A. Fleury and T. C. Damen, Phys. Rev., 1967, 154, 522–526.
45. J. Zhang, M. Li, Z. Feng, J. Chen and C. Li, J. Phys. Chem. B, 2006, 110, 927–935.
46. M. Smirnov and R. Baddour-Hadjean, J. Chem. Phys., 2004, 121, 2348.
47. A. C. Ferrari and J. Robertson, Phys. Rev. B: Condens. Matter Mater. Phys., 2000, 61, 14095–14107.
48. C. Li, J. Catal., 2003, 216, 203–212.
49. G. Busca, G. Ramis, J. M. G. Amores, V. S. Escribano and P. Piaggio, J. Chem. Soc., Faraday Trans., 1994, 90, 3181.
50. Y. M. Lin, P. R. Abel, D. W. Flaherty, J. Wu, K. J. Stevenson, A. Heller and C. B. Mullins, J. Phys. Chem. C, 2011, 115, 2585–2591.
51. A. Auer, E. Portenkirchner, T. Götsch, C. Valero-Vidal, S. Penner and J. Kunze-Liebhäuser, Chem. Mater., 2000 , submitted.
52. W. J. H. Borghols, D. Lützenkirchen-Hecht, U. Haake, E. R. H. van Eck, F. M. Mulder and M. Wagemaker, Phys. Chem. Chem. Phys., 2009, 11, 5742–5748.
53. K. Shen, H. Chen, F. Klaver, F. M. Mulder and M. Wagemaker, Chem. Mater., 2014, 26, 1608–1615.
54. G. V. Zhuang and P. N. Ross, Electrochem. Solid-State Lett., 2003, 6, A136.
55. K. P. Jain, S. Radhakrishna and A. K. Prabhakaran, Phys. Rev. B: Condens. Matter Mater. Phys., 1972, 5, 2325–2328.
56. I. A. Profatilova, C. Stock, A. Schmitz, S. Passerini and M. Winter, J. Power Sources, 2013, 222, 140–149.
57. A. L. Meier, Anal. Chem., 1982, 54, 2158–2161.
58. B. Pritychenko and S. F. Mughabghab, Nucl. Data Sheets, 2012, 113, 3120–3144.
59. D. R. Tilley, C. M. Cheves, J. L. Godwin, G. M. Hale, H. M. Hofmann, J. H. Kelley, C. G. Sheu and H. R. Weller, Nucl. Phys. A, 2002, 708, 3–163.
60. J. Lichtinger, R. Gernhäuser, A. Bauer, M. Bendel, L. Canella, M. Graw, R. Krücken, P. Kudejova, E. Mützel, S. Ring, D. Seiler, S. Winkler, K. Zeitelhack and J. Schöpfer, Med. Phys., 2013, 40, 23501.

---

Footnote

† Electronic supplementary information (ESI) available: Fig. S1–S9. See DOI: 10.1039/c7cp00180k

---