Local structure of a switchable dielectric Prussian blue analogue

Abstract

The Prussian blue (cyanide-bridged, ordered double perovskite) analogue potassium imidazolium hexacyanoferrate, (C₃N₂H₅)₂K[Fe(CN)₆], contains imidazolium cations encapsulated within a metal-cyanide framework. These are free to rotate in the intermediate- and high-temperature phases, but freeze into fixed orientations in the low-temperature phase. The phase transition between intermediate- and low-temperature phases thus causes a substantial change in this material's dielectric constant. However, the detailed cation dynamics, and in particular how they differ between intermediate- and high-temperature phases, remain unclear. We report here total neutron scattering measurements on a perdeuterated sample of this material. Reverse Monte Carlo modelling reveals that the intermediate-temperature phase is associated with a stiffening of the metal-cyanide framework compared to either of the other phases. This shows that the dynamics responsible for the phase transitions involve competition between the energetic penalty for bending the metal-cyanide links and the benefit of host–guest hydrogen bonding. Our results demonstrate both that disordered framework materials have important local structure that is not visible to Bragg scattering, and that there is a crucial link between this structure and the dynamics that give rise to exploitable electric properties.

---

Introduction

The Prussian blues are a diverse family of materials whose simple structure – a cubic network of metal cations linked by cyanide bridges – can produce many useful material properties. The cubic interstices can adsorb or exchange neutral or charged guests, with potential applications including biosensors,¹ photodetectors,² electrodes for Li-³ or Na-ion batteries,^4,5 ion separation membranes,⁶ nuclear waste cleanup materials⁷ and hydrogen storage materials.⁸ There is a strong magnetic exchange interaction through the cyanide anion, and these materials display a range of interesting magnetic properties including photoinduced magnetism.^9,10 Single-molecule magnets have been developed based on nano-sized fragments of the Prussian blue structure.¹¹ Meanwhile, the simple network topology and long, rigid linkers give rise to a series of phase transitions of fundamental interest and can produce anomalous thermal properties such as negative thermal expansion.¹² By varying the charge on the metal cations, the concentration of charged guests or of network defects can be adjusted, influencing all of these properties and leading to phenomena such as spin-glass behaviour.^10,13

Inorganic Prussian blue analogues of chemical formula A^I₂M^I[M^III(CN)₆] have long been known. These compounds tend to have an ordered structure, in which M^I and M^III cations alternate in rock salt fashion to form a cubic framework, and an A cation sits in each cubic interstice for charge balance, giving an overall structure analogous to the mineral elpasolite (K₂NaAlF₆). The bridging cyanide atoms are themselves ordered, forming shorter, more covalent M^III–C bonds, stabilised by π back-bonding, at one end, and longer, more ionic M^I–N interactions at the other. The interstices are large enough to be occupied by a small organic cation A, such as a polymethylammonium or imidazolium; and more recently, several compounds in this category have been reported.^14–16 More generally, these materials are members of the diverse wider family of metal–organic perovskite analogues, in which metals are linked by anions larger than oxide, including bromide, iodide, formate, azide, thiocyanate, or dicyanamide.^17,18

In many of these materials, the high-temperature crystal structure is dynamically disordered, with cations free to rotate. On cooling, a phase transition occurs to a lower-symmetry structure in which the cations are frozen into favourable orientations.¹⁹ Since the cations screen electric fields far more effectively when they are free to rotate, these phase transitions will naturally cause a substantial decrease in the material's dielectric constant. Similarly, since the frozen orientations may have a net dipole moment, these transitions may also involve the onset of ferroelectric order.^20,21 Both of these properties can be exploited for applications in electrical components. Moreover, the versatility of these extended framework structures, in which both framework and guest cations may be readily substituted, will allow these properties to be tuned to meet specific targets.²²

However, the intermolecular forces that give rise to these properties are subtly different from those in the inorganic Prussian blues. Unlike monoatomic metal cations, which induce electric dipole moments by displacement from high-symmetry positions, organic cations may have intrinsic dipole moments. Indeed, they may have higher-order multipole moments, which may have an important influence on the framework symmetry.²³ Furthermore, in addition to these electrostatic interactions, hydrogen bonding between guest and framework will be important in stabilising the various configurations. Understanding structure–property relationships in this family to a level that would enable crystal engineering will require a detailed understanding of both of these effects.

A wide variety of experimental methods have been used to probe these materials' behaviour. Among diffraction methods, X-ray crystallography is a standard and powerful technique, and single crystals of these materials are usually straightforward to produce by solution chemistry methods. However, the standard Bragg scattering formalism only shows the time and space average of the crystal structure, which in disordered phases may be insufficient to characterise the structure in detail. Moreover, X-rays are an unreliable guide to the positions of hydrogen atoms, which are likely to be important in understanding the behaviour of organic guest cations. Neutron diffraction shows hydrogen nuclei clearly, but may require larger samples and expensive deuterated reagents in order to avoid the strong incoherent scattering from the protium nucleus. The Bragg scattering formalism in this case has the same strengths as for X-rays, and the same fundamental weakness: it averages out the local structure.

Alternatively, one might turn to spectroscopic methods, including IR, Raman,²⁴ and solid-state NMR spectroscopy.¹⁵ Such methods have the advantage that they look beyond the crystallographic average in both time and space: NMR (specifically, on the ms–μs timescales relevant to these materials, lineshape analysis) is sensitive to the reorientation dynamics of disordered guests; and vibrational spectroscopy can probe both local (high-frequency) and cooperative (low-frequency) modes. They do not require crystallographic order and are thus equally appropriate for ordered and disordered phases. The principal disadvantage of these methods is that they do not directly give a three-dimensional picture in the same way as diffraction: instead, a model must first be proposed and used to calculate an ideal spectrum which can then be compared with the experimentally observed data.

We here take a third approach that overcomes many of the difficulties associated with both sets of techniques: measurement of total scattering data, comprising Bragg and diffuse scattering together, and analysis by the reverse Monte Carlo (RMC) method. Incorporation of the diffuse scattering makes this technique sensitive to the local as well as the average structure; we conveniently represent local effects by taking the Fourier transform of the scattering data to give the pair distribution function, and requiring that our model reproduces this experimental measurement as well as the intensities of the measured Bragg peaks. This technique is thus highly suitable for use in disordered phases. Using neutron radiation and perdeuterated samples means that our data are sensitive to the position of the hydrogen atoms and hence to the hydrogen bonding. Finally, RMC analysis requires no prior model, and can thus produce atomic configurations consistent with the experimental data without first having to identify candidate models for a material's behaviour. Of course, this method too has disadvantages, of which we mention two in particular here. First, it is expensive in both experimental and computational time. Second, it gives an instantaneous snapshot of a configuration of atoms; while this encodes substantial information about the dynamics of the material, this method is not a direct probe of dynamics.

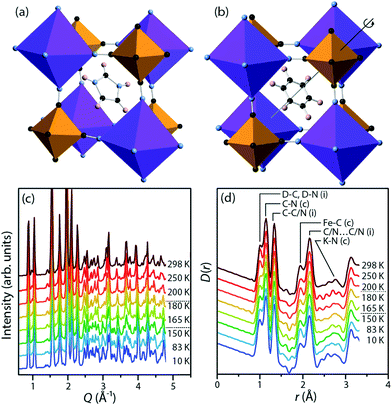
We focus on potassium imidazolium hexacyanoferrate, (C₃N₂H₅)₂K[Fe(CN)₆], a recently discovered material in this family.²⁵ At low temperatures (Fig. 1a), the imidazolium cations in this material are frozen into antiferroelectric order, with no net polarisation. On heating above a phase transition at 158 K, they instead rotate freely within their planes (Fig. 1b). This transition is associated with an increase in space group symmetry from C2/c to R3̄, so that the imidazolium cations are disordered about the threefold axis;²⁶ with a substantial increase in the dielectric permittivity in the plane of the cations; and with a substantial latent heat. This is a cell-doubling transition arising from alternate planes of hexacyanoferrate anions rotating in opposite senses, while the anions themselves remain relatively rigid, a point that will be significant in our analysis below. There is subsequently a second-order phase transition at 187 K to the room-temperature structure, which has space group R3̄m; this is accompanied by a feature in the dielectric permittivity and a small increase in the heat capacity.

Fig. 1 Crystallographic structure of (C₃N₂H₅)₂K[Fe(CN)₆] in (a) the low-temperature C2/c phase, with imidazolium cations frozen into place; (b) the high-temperature R3̄m phase, with imidazolium cations disordered about the threefold axis (indicated) and therefore necessarily modelled as six-membered rings. FeC₆ octahedra are shown in gold, KN₆ octahedra in purple, carbon atoms in black, nitrogen in blue, and hydrogen in pink. (c) The diffraction pattern as a function of temperature. The phase transitions are indicated by dotted lines. (d) The pair distribution function D(r) as a function of temperature, with major peaks identified. Again, the phase transitions are indicated by dotted lines. Here (c) refers to the cyanide ion and (i) to the imidazolium ion.

Understanding this material's behaviour in the dielectric phases depends crucially on measuring its local structure, for two reasons. First, in these phases the imidazolium cations are disordered about crystallographic threefold axes, and indeed have been modelled in single-crystal diffraction analyses as six-membered rings: a clear example of a chemically impossible average structure. Second, the difference between the intermediate- and high-temperature structures is the presence at high temperature of a crystallographic mirror plane through the cyanide ligand. It would, however, be severely misleading to rely on the average structure and imagine that the cyanide atoms are displaced away from the plane only in the intermediate-temperature phase. Rather, they must be in constant motion about the plane at all temperatures, but with a greater correlation length in the intermediate-temperature phase. Thus techniques such as total neutron scattering and RMC modelling provide a unique and important way to understand the structural changes in this material.

Methods

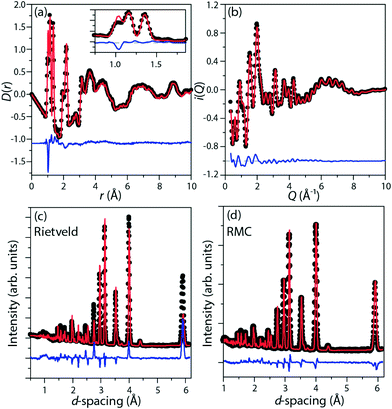
Perdeuterated (DIm)₂K[Fe(CN)₆] was synthesised by literature methods.²⁵ Total neutron scattering data were collected using the POLARIS instrument (ISIS, U.K.; Fig. 1c and d). The data were corrected and normalised to give the scattering function i(Q), and the pair distribution function D(r) calculated by taking the sine Fourier transform over the Q range 0.30 Å to 46.0 Å⁻¹, using GUDRUN.²⁷ Rietveld refinement was performed starting from literature structures using the EXPGUI²⁸ interface to GSAS.²⁹ Configurations consistent with i(Q) and D(r) and with the observed Bragg peaks were produced by the reverse Monte Carlo method (RMC) as implemented in a modified version of RMCProfile.³⁰ The simulation supercells were 50 Å to 60 Å in each linear dimension and contained 11 016 (rhombohedral) or 13 056 (monoclinic) atoms. The initial configurations were generated from Rietveld-refined crystal structures, with imidazolium rings randomly oriented in their plane in the disordered phases. Interatomic potentials governing bond stretching and bending and the planarity of the imidazolium cation were applied to the organic components (imidazolium and cyanide) only, to ensure the refined configurations represented chemically plausible structures; see ESI† for full details. To minimise statistical noise, for each data set 25 unique RMC configurations were produced and analysed. The refinements were considered converged when continued random atomic moves no longer improved agreement between the model and the data, which typically occurred after 4.5 × 10⁶ (rhombohedral) or 6.4 × 10⁶ (monoclinic) atomic moves had been accepted.

A symmetry analysis of the low-to-intermediate temperature phase transition was performed using the online tools of the Bilbao Crystallographic Server.^31–33 Our analysis shows that this is a zone-boundary (cell-doubling) transition with active irrep L₁⁻, where L = (½, 0, 0) in terms of the rhombohedral cell.

Representative fits are given in Fig. 2.

Fig. 2 Representative RMC-refined fits in the high-temperature phase (298 K) to (a) the pair distribution function D(r); (b) the total scattering function i(Q). The Rietveld-refined fit to the diffraction pattern (c), with disordered imidazolium cations modelled as benzene rings, has substantially higher residual than the RMC-refined fit to the same data (d), which allows a more accurate model of this disorder.

Results

In this material, both the metal-cyanide framework and the imidazolium guests can contribute to the electric dipole moment: in addition to the intrinsic dipole moment of the imidazolium cation, either the imidazolium or the metal cations may produce a dipole moment by moving away from the centre of their respective coordination environments. In the average structure of the low-temperature C2/c phase, the iron cations remain at the centre of the FeC₆ coordination octahedra. The potassium cations are displaced by 0.2 Å along the crystallographic b axis from the centroid of the KN₆ coordination octahedra. The intrinsic imidazolium dipole moment points in approximately the [021̄] direction. The refined RMC configurations were analysed for each of these effects separately. Here we consider first the cation dynamics, then the flexibility of the metal cyanide framework, and finally the local correlations between the framework and its cationic guests.

Two different motions of the imidazolium cations were isolated from the refined atomic configurations: rotation in the plane of the molecule and tilting out of that plane. Considering rotation, in the intermediate- and high-temperature phases, the orientation of the imidazolium dipole moment was initially random, with a uniform distribution in the plane. RMC refinement produced no change in this distribution, suggesting that the cations rotate freely rather than hopping between allowed orientations. This contrasts with the isotopological framework material dimethylammonium manganese(II) formate, in which both Bragg and RMC analysis indicate an energy barrier between rotational orientations of the organic cation.³⁴

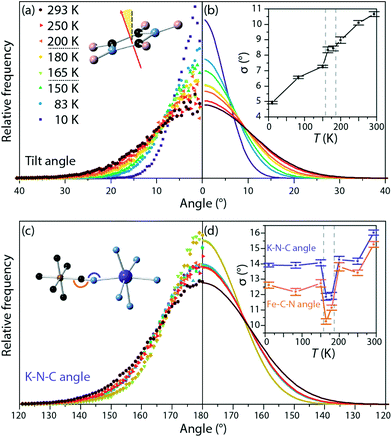
Similarly, the tilt of the imidazole rings out of their mean plane was calculated for all phases (Fig. 3a and b). The width of the distribution of tilt angles increased with temperature, but no discontinuous change was observed at either phase transition. This contrasts with previously reported NMR measurements on the Co analogue to this material, which we discuss in more detail below.¹⁵

Fig. 3 (a) Distribution of tilt angles of the imidazolium cations at different temperatures. (b) Gaussian fits to the data in (a). The inset shows the standard deviation σ of these fits as a function of temperature. (c) Distribution of K–N≡C angles at different temperatures. (d) Gaussian fits to the data in (c). The inset shows the standard deviation σ of these fits (purple) and the equivalent data for Fe–C–N angles (gold). Error bars in the insets show the 95% confidence limit of σ. All frequencies in this figure have been normalised to constant solid angle by dividing by sin θ.

Distortions in the metal-cyanide framework were monitored via the distributions of N–K–N and C–Fe–C angles of the coordination octahedra; of the Fe–C≡N and K–N≡C angles of the cyanide linkers; and of the distances between the imidazole cations and the cyanide N atoms in the same plane. The distribution of angles within the KN₆ and FeC₆ octahedra was approximately Gaussian and centred on 90° and 180° at all temperatures; the breadth of the distribution was almost independent of temperature (see ESI†). At all temperatures, the distribution of the angles in the essentially ionic KN₆ octahedra was broader than in the more covalent FeC₆ octahedra, in accordance with the expectation that more ionic environments can accommodate a wider range of coordination geometries. This is consistent with the low-temperature average structure, in which the K atom moves off-centre as noted previously, and with the cobalt analogue of this material.

The Fe–C≡N and K–N≡C angles were similarly monitored and fit to a Gaussian centred on 180° (Fig. 3c and d). At all temperatures the distribution of angles is broader for the K–N≡C angles than for the Fe–C≡N bond angles, showing greater deformation about the K site; again, this is expected from considerations of the covalency of the two metal-cyanide bonds and from these angles in the low-temperature phase (K–N≡C: 167° to 168°, more distorted than Fe–C≡N: 176° to 177°). More unexpectedly, at both sites, the distribution narrows substantially in the intermediate temperature phase. This narrowing of the distribution of angles indicates that in the intermediate temperature phase, the framework is more rigid than in either of the other two phases. This is consistent with the observation that, to explain the R3̄ structure of the intermediate-temperature phase, the correlation length associated with cyanide deviations away from the high-temperature mirror plane must be high. Direct observation of this purely local effect, however, could not have been achieved from average structural information – i.e., Bragg diffraction data – alone.

Fig. 4 shows the distribution of distances between cyanide N atoms and the centroid of the imidazole ring, a measure of the extent to which the framework distorts around the cation. In the low-temperature phase, three atoms ((i), pink) are close to the centroid (3.88 Å to 4.00 Å), six ((ii), brown) are slightly further away (4.06 Å to 4.18 Å), and three ((iv), blue) are much further away (4.60 Å to 4.68 Å). In the high-temperature phase, three [Fe(CN)₆]³⁻ anions rotate so that the equatorial atoms ((iii), green) adopt a new, intermediate distance (4.38 Å). The distribution of distances as a function of temperature shows that this is not a sharp effect at either phase transition, but instead a gradual transition. As the temperature increases and the unit cell becomes closer to the ideal cubic case, the “near” peak (ii) and “far” peak (iv) both gradually diminish while the intermediate peak (iii) grows.

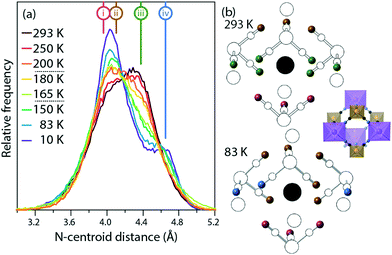Fig. 4 (a) Distribution of centroid⋯N distances from the imidazolium to the framework. The distances in the average crystal structure of the high- and low-temperature phases are labelled (i)–(iv). (b) Average crystal structures of the high- and low-temperature phases. The imidazolium cation is shown as a black circle at the centroid, nitrogen atoms are shown as colored spheres corresponding to the labelled distances (i)–(iv), and all other atoms are shown in white. For ease of comparison, the inset shows the structure in the same orientation, but with the colour scheme of Fig. 1.

Discussion

Our results can be rationalised by a simple qualitative model in which the important interactions are hydrogen bonding between the guest and framework (favourable) and the deformation of metal-cyanide angles (unfavourable). In the low-temperature phase, both hydrogen bonds and framework distortion are present. In the intermediate-temperature phase, the host–guest hydrogen bonds break, allowing the framework to return closer to an ideal linear metal-cyanide geometry; the energy gain is compensated by the entropic stabilisation from the imidazolium cations now being free to rotate. Finally, in the high-temperature phase, the metal-cyanide bond angles begin to distort independently and dynamically, again with an associated entropic benefit. The cooperative distortion in the intermediate-temperature phase is likely to arise in part from the mechanical rigidity of both the FeC₆ and the KN₆ octahedra, which couple the host–guest interactions in one interstice with those in its neighbors.

We now compare our results with literature data on the cobalt analogue of this material. The cobalt compound displays two similar phase transitions, but there are nonetheless important differences between the cobalt and iron compounds' behavior. In particular, the intermediate-temperature phase is stable over a wider temperature range for the cobalt (112 K to 198 K) than the iron compound (158 K to 187 K). We have previously rationalised this in terms of the smaller Co–CN bond length than Fe–CN.²⁶ In light of the present results, we note too that the Co–C≡N bond angle is stiffer than Fe–C≡N.³⁵ This also might be expected to stabilise the intermediate-temperature phase, in which these angles are closer to their ideal linear values, with respect to both of the other two phases.

The difference between the intermediate- and high-temperature data has been attributed in the Co compound, based on ²H-NMR spectroscopy, to the onset of imidazolium tilting at that phase transition.¹⁵ As we note above, in the Fe compound our RMC modelling shows imidazolium tilting at all temperatures, without a sharp increase at the phase transition. This is not a direct contradiction since, as well as the difference in the metals in the two studies, our Fe compound was perdeuterated while Zhang et al. used the Co compound in partially deuterated form, with ²H at the imidazolium C but not N atoms. The effect of deuteration on hydrogen bonding may be significant, even though it is unlikely to alter the energy of the hydrogen bond itself by a large amount, since the phase transition involves competing interactions with similar energies, and a small change in one interaction may change which one predominates. Nonetheless, further investigation of this apparent discrepancy would be worthwhile.

Conclusion

In summary, we have used total neutron scattering and reverse Monte Carlo modelling to investigate the dynamics of the framework and guest cations in the Prussian blue analogue potassium imidazolium hexacyanoferrate(III) as it transitions from an electrically disordered to an ordered state. There was no indication of preferred orientation of the imidazolium relative to the framework above the dielectric transition temperature. The imidazolium is dynamically disordered in both the high- and intermediate-temperature phases. It tilts about the plane of rotation in all phases, and while there is a gradual increase in the breadth of the distribution of tilt angles with increasing temperature, no abrupt change is observed at either phase transition. The distribution of metal-cyanide angles is narrower in the intermediate-temperature phase than in either the high- or low-temperature phases.

Our results reveal several instances in which characterising the phases by their long-range crystallographic symmetry gives a picture that is at best incomplete and at worst may be actively misleading. The difference between the high- and intermediate-temperature phases is best understood in terms of rigidity of the iron-cyanide bond angle, affecting the correlation length associated with cyanide tilting. Similarly, the tilt of the hexacyanoferrate ions, as measured by the distance between the cyanide nitrogen atom and the imidazolium ion centroid, changes gradually with temperature rather than abruptly at a phase transition. We suggest in fact that the average (Bragg) crystal structure is in general inadequate to describe the structure of disordered metal–organic frameworks. We have furthermore demonstrated that the dynamics of this material are governed by the competing energetic benefits of forming host–guest hydrogen bonds and having linear metal-cyanide linkers. In other words, there is a crucial link between the local structure of this material and the dynamics responsible for its remarkable dielectric properties. Understanding these dynamics will contribute to crystal engineering of new materials in this family, helping to tune the phase transition temperatures and changes in dielectric constant for particular applications.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

We thank the ISIS Neutron and Muon Source for beamtime and EPSRC for provision of the MidPlus high-performance computing system on which the calculations were performed (EP/K000233/1, EP/K000128/1) and for funding (A. E. P., EP/L024977/1). We further acknowledge studentships from the STFC (H. D. D.) and EPSRC (E. O. R. B.).

References

1. Z.-D. Gao, Y. Qu, T. Li, N. K. Shrestha and Y.-Y. Song, Sci. Rep., 2014, 4, 6891.
2. L. Han, L. Bai and S. Dong, Chem. Commun., 2013, 50, 802–804.
3. P. Nie, L. Shen, H. Luo, B. Ding, G. Xu, J. Wang and X. Zhang, J. Mater. Chem. A, 2014, 2, 5852–5857.
4. H.-W. Lee, R. Y. Wang, M. Pasta, S. Woo Lee, N. Liu and Y. Cui, Nat. Commun., 2014, 5, 5280.
5. S. Jiao, J. Tuo, H. Xie, Z. Cai, S. Wang and J. Zhu, Mater. Res. Bull., 2017, 86, 194–200.
6. M. Pyrasch, A. Toutianoush, W. Jin, J. Schnepf and B. Tieke, Chem. Mater., 2003, 15, 245–254.
7. P. A. Haas, Sep. Sci. Technol., 1993, 28, 2479–2506.
8. L. J. Murray, M. Dinca and J. R. Long, Chem. Soc. Rev., 2009, 38, 1294–1314.
9. O. Sato, T. Iyoda, A. Fujishima and K. Hashimoto, Science, 1996, 272, 704–705.
10. A. Bleuzen, C. Lomenech, V. Escax, F. Villain, F. Varret, C. Cartier dit Moulin and M. Verdaguer, J. Am. Chem. Soc., 2000, 122, 6648–6652.
11. M. Ohba and H. Okawa, Coord. Chem. Rev., 2000, 198, 313–328.
12. S. Adak, L. L. Daemen, M. Hartl, D. Williams, J. Summerhill and H. Nakotte, J. Solid State Chem., 2011, 184, 2854–2861.
13. Y. Yang, E. Liu, X. Yan, C. Ma, W. Wen, X.-Z. Liao and Z.-F. Ma, J. Electrochem. Soc., 2016, 163, A2117–A2123.
14. W. Zhang, H.-Y. Ye, R. Graf, H. W. Spiess, Y.-F. Yao, R.-Q. Zhu and R.-G. Xiong, J. Am. Chem. Soc., 2013, 135, 5230–5233.
15. X. Zhang, X.-D. Shao, S.-C. Li, Y. Cai, Y.-F. Yao, R.-G. Xiong and W. Zhang, Chem. Commun., 2015, 51, 4568–4571.
16. W.-J. Xu, S.-L. Chen, Z.-T. Hu, R.-B. Lin, Y.-J. Su, W.-X. Zhang and X.-M. Chen, Dalton Trans., 2016, 45, 4224–4229.
17. W. Li, Z. Wang, F. Deschler, S. Gao, R. H. Friend and A. K. Cheetham, Nat. Rev. Mater., 2017, 2, 201699.
18. G. Kieslich and A. L. Goodwin, Mater. Horiz., 2017, 4, 362–366.
19. W.-J. Xu, Z.-Y. Du, W.-X. Zhang and X.-M. Chen, CrystEngComm, 2016, 18, 7915–7928.
20. M. Guo, H.-L. Cai and R.-G. Xiong, Inorg. Chem. Commun., 2010, 13, 1590–1598.
21. W.-J. Xu, P.-F. Li, Y.-Y. Tang, W.-X. Zhang, R.-G. Xiong and X.-M. Chen, J. Am. Chem. Soc., 2017, 139, 6369–6375.
22. C. Shi, C.-H. Yu and W. Zhang, Angew. Chem., Int. Ed., 2016, 55, 5798–5802.
23. N. L. Evans, P. M. M. Thygesen, H. L. B. BostrÃűm, E. M. Reynolds, I. E. Collings, A. E. Phillips and A. L. Goodwin, J. Am. Chem. Soc., 2016, 138, 9393–9396.
24. M. Maczka, N. L. M. Costa, A. Gagor, W. Paraguassu, A. Sieradzki and J. Hanuza, Phys. Chem. Chem. Phys., 2016, 18, 13993–14000.
25. W. Zhang, Y. Cai, R.-G. Xiong, H. Yoshikawa and K. Awaga, Angew. Chem., Int. Ed., 2010, 49, 6608–6610.
26. A. E. Phillips and D. Fortes, Angew. Chem., Int. Ed., 2017 DOI:10.1002/anie.201708514.
27. A. K. Soper, GudrunN and GudrunX: Programs for Correcting Raw Neutron and X-Ray Diffraction Data to Differential Scattering Cross Section, https://epubs.stfc.ac.uk/work/56240.
28. B. H. Toby, J. Appl. Crystallogr., 2001, 34, 210–213.
29. A. C. Larson and R. B. Von Dreele, General Structure Analysis System (GSAS).
30. M. G. Tucker, D. A. Keen, M. T. Dove, A. L. Goodwin and Q. Hui, J. Phys.: Condens. Matter, 2007, 19, 335218.
31. M. I. Aroyo, A. Kirov, C. Capillas, J. M. Perez-Mato and H. Wondratschek, Acta Crystallogr., Sect. A: Found. Crystallogr., 2006, 62, 115–128.
32. M. I. Aroyo, J. M. Perez-Mato, C. Capillas, E. Kroumova, S. Ivantchev, G. Madariaga, A. Kirov and H. Wondratschek, Z. Kristallogr., 2009, 221, 15–27.
33. M. I. Aroyo, D. Orobengoa, G. de la Flor, E. S. Tasci, J. M. Perez-Mato and H. Wondratschek, Acta Crystallogr., Sect. A: Found. Adv., 2014, 70, 126–137.
34. H. D. Duncan, M. T. Dove, D. A. Keen and A. E. Phillips, Dalton Trans., 2016, 45, 4380–4391.
35. I. Nakagawa and T. Shimanouchi, Spectrochim. Acta, 1962, 18, 101–113.

---

Footnotes

† Electronic supplementary information (ESI) available: Data collection run numbers and full details of data processing and analysis. See DOI: 10.1039/c7ce01883e

‡ Current address: Centre for Science at Extreme Conditions, The University of Edinburgh, Peter Guthrie Tait Road, King's Buildings, Edinburgh EH9 3FD, UK.

---