Influence of composition on the isothermal crystallisation of segmented thermoplastic polyurethanes†
Abstract
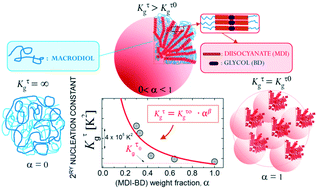
The isothermal crystallisation of a series of segmented thermoplastic polyurethanes (TPUs) composed of 4,4′-methylene bisphenyl diisocyanate (MDI)-1,4-butanediol (BD) segments has been studied in detail. The influence of MDI-BD content within the TPUs on the nucleation, growth and resulting morphology has been analyzed by converging the results obtained from differential scanning calorimetry (DSC), polarised light optical microscopy (PLOM), synchrotron X-ray small angle scattering (SAXS), and atomic force microscopy (AFM). The materials crystallised from a single phase melt, as evidenced by SAXS. The increase of just 13 wt% in MDI-BD content leads to an increment of 4 orders of magnitude in the nucleation density and nucleation rate. In addition, the increase of MDI-BD content also enhances the spherulitic growth rate and overall crystallisation kinetics. The overall isothermal crystallisation kinetics determined by DSC can be described in an unusually large conversion range (i.e., beyond primary crystallisation) using the Avrami equation. The increase of the isothermal crystallisation temperature changes the superstructural morphology from spherulitic to axialitic, and therefore the Avrami index is reduced from approximately 3 to 2. Negative spherulites with the crystallographic c axis oriented tangentially to the spherulite were observed by PLOM and the spherulitic texture details were revealed by AFM and SAXS as a radial lamellar-like assembly of the MDI-BD segments. The energy barrier for nucleation and growth decreased exponentially with the increase in MDI-BD content. Finally, from all the evidence gathered here, a morphological schematic picture of the hierarchical structure of TPUs upon crystallisation is presented. The results presented in this report pave the way for a comprehensive guide to developing materials with the desired structure, based on the understanding of the intricate relationship between crystallinity, thermal history and composition of TPUs.


 Please wait while we load your content...
Please wait while we load your content...