Temperature dependent excited state relaxation of a red emitting DNA-templated silver nanocluster

Abstract

The nanosecond excited state temporal and spectral relaxation of a purified, red-emitting DNA-templated silver nanocluster (DNA–AgNC) was characterized as a function of temperature. The findings are explained by introducing a phenomenological electronic structure diagram. The reproducibility and cyclability of the average decay time opens up the possibility of using DNA–AgNCs for decay time-based nanothermometry.

---

DNA–AgNCs are fluorescent emitters comprising a few silver atoms (typically <25) stabilized by a single stranded DNA scaffold.¹ Their brightness, photostability and wavelength tunability have encouraged their use as sensors and fluorophores in imaging applications.^2–7 Despite the increase in the number of applications, the relationship between the DNA sequence, the AgNC structure and its final photophysical properties is still an active area of research.^8–11 In particular, the DNA scaffold appears to have an important influence on the solvation dynamics of the DNA–AgNCs.^12,13 After the initial sub-picosecond relaxation accounting for most of the Stokes shift, the fluorescence spectra undergo red-shift on a nanosecond time scale.^14–18 As shown in a previous study,¹⁸ the increase of the average decay time as a function of wavelength in purified DNA–AgNCs can be explained by a spectral relaxation. This phenomenon can be convoluted with other phenomena e.g. multiple emitters in non-purified samples.^15,19 Here, we studied the effect of temperature on the nanosecond spectral relaxation dynamics of DNA–AgNCs in 10 mM ammonium acetate (NH₄OAc). Besides giving insight on the spectral relaxation process, this study also demonstrates that the average decay time of DNA–AgNCs could find applications in nanothermometry,²⁰ where nanoscale probes are used as local thermometers.²¹ Therefore, we investigated the performance of the average decay time of DNA–AgNCs as a temperature probe in the temperature range of 5–60 °C together with its stability and cyclability. Although nucleic acid based nanothermometers have been previously reported,²² to the best of our knowledge, the use of DNA–AgNCs in thermometry applications has not been reported.

In this work we used a cytosine rich DNA sequence 5′-TTCCCACCCACCCCGGCCC-3′. This sequence is a shortened version of the sequence 5′-TTCCCACCCACCCCGGCCCGTT-3′ previously studied by Gwinn et al.^8,12,13,23 The removal of the three terminal bases does not seem to change the spectral properties of the DNA–AgNC suggesting that they were not involved in stabilizing the AgNC. After the synthesis of DNA–AgNCs, the sample was purified by HPLC (see Fig. S1, ESI†) where the fraction with a retention time of 9 minutes was obtained. The DNA–AgNCs show an absorption maximum at 573 nm and an emission maximum around 640 nm (Fig. 1). The 2D excitation versus emission plot (Fig. S2, ESI†) shows that the DNA–AgNC appears like a single emissive species. The purified DNA–AgNCs possess good long term stability as evidenced from the very similar absorption spectra measured for a freshly purified sample compared to the same sample one month after synthesis (Fig. S3, ESI†). The fluorescence quantum yield was determined to be 0.80 at 25 °C.²⁴ As shown in Fig. 1, increasing the temperature of the solution from 5 °C to 40 °C causes a red-shift of a few nanometers in the steady state emission spectrum, while the absorption spectrum does not shift significantly. This indicates that temperature mainly affects the excited state relaxation process. An overview of the fluorescence quantum yield, absorption and emission maxima at 5 °C, 25 °C and 40 °C can be found in Table 1.

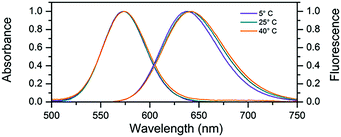Fig. 1 Normalized absorption and steady-state emission at various temperatures. For the emission spectra, the DNA–AgNC sample was excited at 561 nm.

Table 1 Absorption and emission maxima, λ_abs (max) and λ_em (max), weighted average fluorescence decay time, 〈τ_w〉, and fluorescence quantum yield, QY, at different temperatures

	5 °C	25 °C	40 °C
a Average decay time, weighted by the intensity over the whole emission range. b Cresyl violet in ethanol was used as a reference.
λ abs (max)	573 nm	573 nm	574 nm
λ em (max)	638 nm	640 nm	642 nm
〈τw〉^a	2.7 ns	2.59 ns	2.47 ns
QY^b	0.88	0.80	0.70

---

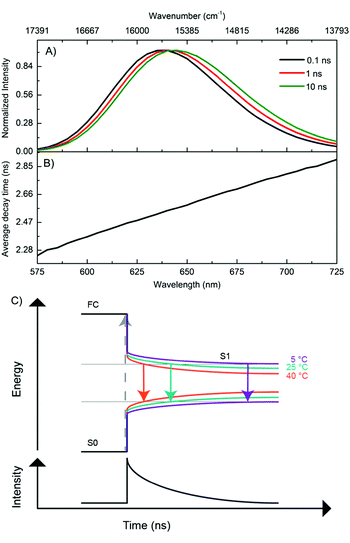
In order to better understand the excited-state relaxation process, we performed time-correlated single photon counting (TCSPC) measurements as a function of emission wavelength at 5 °C, 25 °C and 40 °C on the purified DNA–AgNCs. This allowed construction of time-resolved emission spectra (TRES) and average decay time spectra for the different temperatures.^18,19 Although the steady-state 2D plot indicates a single emitter (Fig. S2, ESI†), a three-exponential model was necessary to fit the globally linked fluorescence decay curves. Due to the spectral relaxation during the time course of the excited state decay, the derived decay associated spectra (DAS) present meaningless components, of which the fastest are usually characterized by negative amplitudes at long wavelengths (Fig. S4, ESI†). This behavior is similar to another purified red emitting DNA–AgNC studied previously.¹⁸ Replotting the same data in the TRES form reveals a continuous red-shift of the emission spectrum with negligible broadening (Fig. 2A). As a result of this continuous red-shift, the average decay time 〈τ〉 increases with emission wavelength (Fig. 2B). This behavior can be found at 5 °C, 25 °C and 40 °C. All these features indicate the presence of a slow changing environment or restructuring of the DNA–AgNC, which is slower than the commonly observed picosecond solvation dynamics of more classical fluorophores in water.²⁵ The scheme proposed in Fig. 2C shows the effect of relaxation on the absorptive and emissive states as a function of time and temperature and combines the steady state observations in Fig. 1 with the continuous spectral relaxation in Fig. 2A. As the temperature increases, the excited state relaxes faster and to a lower energy. The 〈τ〉 decreases as a function of increasing temperature across the whole emission range, as shown in Fig. 4B. Whether the increase in spectral relaxation upon increasing the temperature is solely due to the increased thermal energy (kT) or also due to the decreased viscosity should be explored in further studies. In order to gain insight into the effect of temperature on 〈τ〉, we measured the quantum yield (QY) and calculated the intensity weighted average decay time 〈τ_w〉 from the average decay time spectrum, at 5 °C, 25 °C and 40 °C (Table 1). These experimental values of QY are plotted against 〈τ_w〉 (Fig. 3A, circles) and can be fitted to a linear model (Fig. 3A, blue line). Remarkably, the fit intersects the QY = 0 line at a value of 〈τ_w〉 = 1.55 ns instead of 〈τ_w〉 = 0 (red line), which would be expected from the classic equation QY = k_f 〈τ_w〉.²⁵

Fig. 2 (A) Time-resolved emission spectra of DNA–AgNCs at 25 °C, excited at 561 nm. (B) The average decay time as a function of emission wavelength of DNA–AgNCs at 25 °C, excited at 561 nm. (C) Top: a Jablonski diagram of DNA–AgNCs at different temperatures. The dashed arrow represents the absorption process. Solid arrows represent fluorescence of a specific emission energy which is reached faster at higher temperatures due to faster relaxation. The top diagram illustrates the spectral relaxation during the decay process. Relative energy differences are exaggerated for display purposes. Bottom: time-resolved emission intensity, representing the decay of the DNA–AgNCs from the S₁ to S₀ state.

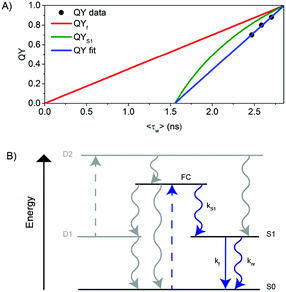Fig. 3 (A) QY versus 〈τ_w〉 for scenario I (see also Fig. S5, ESI†). (B) Schematic representation of the electronic structure of the DNA–AgNC. Blue arrows indicate the processes probed in this paper. Gray arrows indicate the processes not probed in this paper but inferred based on literature data. The decay pathway from S₁ to S₀ as a function of time and temperature can be visualized in more detail in Fig. 2C.

We explain this effect using a generalized phenomenological AgNC electronic structure model, which is shown in Fig. 3B and is based on previous photophysical studies on DNA–AgNCs.^4,6,26 From the Franck–Condon state (FC) right after absorption of a photon, the system evolves to either the ground state (S₀), a dark state (D₁) or to the emissive state (S₁) on a time scale that cannot be resolved with TCSPC equipment used here, but is demonstrated in literature data.^26,27 The dark state D₁ usually has a decay time in the tens of microseconds range and can be used to modulate the fluorescence or generate delayed fluorescence from S₁ through secondary absorption of a photon.^4,6 However, in this study, we are only monitoring the pathways indicated by the blue arrows. Therefore, we rewrite the measured fluorescence steady state quantum yield (QY) as QY = QY_S1·QY_f where QY_S1 is the quantum yield of S₁ formation and QY_f = k_f·〈τ_w〉 is the quantum yield of fluorescence from the S₁ state.²⁸ This model could also help explain the usual nanosecond decay time reported in the literature for DNA–AgNCs, seemingly uncorrelated to the corresponding QY and molar absorption coefficient.^29,30 From the fit to our data, 〈τ_w〉 = 2.86 ns for QY = 1. Since at this point QY = 1 (hence also QY_f and QY_S1 must be 1), we can calculate the value of k_f at QY = 1 to be k^100%_f = 3.5 × 10⁸ s⁻¹ and plot QY_f assuming a constant k^100%_f (red curve) and QY_S1 (green curve) for comparison with our data. The fact that our data was fitted with a linear function of the form QY = a〈τ_w〉 − b, where a,b > 0 implies that QY_S1·k_f = a − b/〈τ_w〉. Since it is not known a priori which of the values (QY_S1 or k_f or both) change with temperature, there are three different possible scenarios that could explain the blue line in Fig. 3A.

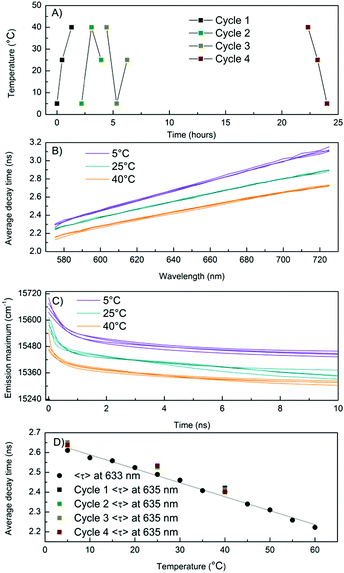
In Scenario I (Fig. 3A and Fig. S5, ESI†), the value of k_f is assumed to be constant and has the value k^100%_f. This implies that QY_S1 (green line) decreases as a function of temperature faster than QY_f (red line) and is responsible for a faster decrease of the measured total QY. Interestingly, this would allow the observed 〈τ_w〉 to remain in the nanosecond range, even close to a QY of zero. The non-radiative rate k_nr = (1/〈τ_w〉) − k_f also increases as a function of temperature in this scenario. In Scenario II (Fig. S6, ESI†), QY_S1 is constant, likely at or close to 1 (since we measured a value of QY = 0.9 at 5 °C), and the decrease in k_f and the increase in k_nr are responsible for the QY trend. In Scenario III (Fig. S7, ESI†), both variables (QY_S1 and k_f) change as a function of temperature in such a way that the linear relationship between QY and 〈τ_w〉 holds. The latter seems unlikely. We currently believe that Scenario I is the most plausible. However, further investigations are needed for a more conclusive answer. In order to assess the reproducibility and cyclability of the temperature response, we measured TRES data while cycling the temperature between 5 °C, 25 °C and 40 °C four times in different orders and in a time span of 25 hours (Fig. 4A). Note that the sample was stored in a fridge between cycle 3 and cycle 4. The average decay time spectra (Fig. 4B) of the four cycles show a very similar slope for the three temperatures, and a temperature dependent offset. The average decay times were extracted from a tri-exponential global fit with linked decay times. The spectral shift of the emission maxima was interpolated from the TRES.

Fig. 4 (A) Temperature cycles applied to DNA–AgNCs during the TCSPC measurements. (B) Average decay time of DNA–AgNCs as a function of the emission wavelength for every cycle of measurement at various temperatures. (C) Emission maximum shift over time for every cycle of measurement at different temperatures. The excitation wavelength was 561 nm. (D) Average decay time of DNA–AgNCs as a function of temperature. The black line is the calibration curve (linear fit) from the average decay time values obtained by fitting single decay curves detected at 633 nm with a bi-exponential model (circular data points). The average decay times from the TRES data at 635 nm in B are also reported in the graph as square data points. The excitation wavelength was 561 nm.

These relaxation dynamics of the emission maximum usually comprise a fast component in the order of hundred picoseconds and slower components in the nanosecond range (see Fig. 4C). This is in agreement with previous studies.^15,17,18 The spectral shifts measured while cycling the temperature are shown in Fig. 4C. The time resolved emission maxima clearly decrease as a function of increasing temperature, in line with the steady state measurements (Fig. 1). The starting value of the emission maxima at t = 0 also decreases as a function of temperature. As the absorption remains constant over this temperature range, the emission maxima at t = 0 at all the temperatures should in principle be the same. However, in our TCSPC experiments we cannot observe the initial fast spectral relaxation due to the IRF limited response of the equipment ≈150 ps. This is in agreement with previous ultrafast spectroscopy studies which show that the electronic relaxation from the absorbing state to the emissive state occurs on a sub-picosecond timescale.^14,26,27 The time-resolved measurements demonstrate the reproducible and reversible temperature response of the AgNCs. It also validates the thermal stability of the DNA–AgNCs in the probed temperature range of 5–40 °C, as shown in Fig. 4. Together with previous studies in the literature, this indicates that the nanosecond spectral relaxation could be a common feature in DNA–AgNCs.^15,17–19 Next, we studied the temperature dependent change of 〈τ〉 in more detail. For this, a new batch of the same DNA–AgNCs was synthesized under the same conditions. Now, only single decay curves at λ_exc = 561 nm and λ_em = 633 nm were measured while varying the temperature from 5 °C to 60 °C, in steps of 5 °C (Fig. S8, ESI†). The curves were fitted with a bi-exponential fluorescence decay model in order to determine 〈τ〉. Fig. 4D shows 〈τ〉 plotted as a function of temperature (black circles) which can be fitted with a linear function (solid black line) in this extended temperature range. The decay time values from the previous sample (Fig. 4B) at λ_em = 635 nm, plotted in the same graph (Fig. 4D, square markers) fall close to the fit, indicating a high degree of reproducibility. Using the linear fit in Fig. 4D as a calibration curve for thermometer applications, and using the formula (Δ〈τ〉/ΔT)/〈τ〉_max,³¹ we can estimate a sensitivity value with respect to the highest decay time of S = 0.0027 °C⁻¹ at a temperature range of 5–60 °C. This is about five times less than that of the well known Rhodamine B example which has S = 0.0127 °C⁻¹ at a temperature range of 10–70 °C (see ESI†).²⁰ Since this is the first reported example of DNA–AgNCs, it is likely that there might be other examples with higher sensitivity and biocompatibility, opening up possibilities for in vitro and in vivo thermometry.⁵

In conclusion, we have studied the fluorescence decay of DNA–AgNCs as a function of temperature, and found that they can be used as decay time based nanothermometers. Further systematic studies with different sequences may improve the performance of such thermometers and could explain if viscosity also plays a role.

We gratefully acknowledge financial support from the “Center for Synthetic Biology” at Copenhagen University funded by the UNIK research initiative of the Danish Ministry of Science, Technology and Innovation (Grant 09-065274), bioSYNergy, the University of Copenhagen's Excellence Programme for Interdisciplinary Research, the Villum Foundation (Project number VKR023115), the Danish Council of Independent Research (Project number DFF-7014-00027), and the Carlsberg Foundation (CF14-0388).

Conflicts of interest

There are no conflicts to declare.

Notes and references

1. E. Gwinn, D. Schultz, S. M. Copp and S. Swasey, Nanomaterials, 2015, 5, 180–207.
2. L. Zhang and E. Wang, Nano Today, 2014, 9, 132–157.
3. S. W. Yang and T. Vosch, Anal. Chem., 2011, 83, 6935–6939.
4. C. I. Richards, J. C. Hsiang, D. Senapati, S. Patel, J. Yu, T. Vosch and R. M. Dickson, J. Am. Chem. Soc., 2009, 131, 4619–4621.
5. J. Yu, S. Choi, C. I. Richards, Y. Antoku and R. M. Dickson, Photochem. Photobiol., 2008, 84, 1435–1439.
6. B. C. Fleischer, J. T. Petty, J.-C. Hsiang and R. M. Dickson, J. Phys. Chem. Lett., 2017, 8, 3536–3543.
7. N. Enkin, F. Wang, E. Sharon, H. B. Albada and I. Willner, ACS Nano, 2014, 8, 11666–11673.
8. S. M. Copp, D. Schultz, S. Swasey, J. Pavlovich, M. Debord, A. Chiu, K. Olsson and E. Gwinn, J. Phys. Chem. Lett., 2014, 5, 959–963.
9. S. M. Copp, P. Bogdanov, M. Debord, A. Singh and E. Gwinn, Adv. Mater., 2014, 26, 5839–5845.
10. J. T. Petty, O. O. Sergev, M. Ganguly, I. J. Rankine, D. M. Chevrier and P. Zhang, J. Am. Chem. Soc., 2016, 138, 3469–3477.
11. J. T. Petty, M. Ganguly, I. J. Rankine, D. M. Chevrier and P. Zhang, J. Phys. Chem. C, 2017, 121, 14936–14945.
12. S. M. Copp, A. Faris, S. M. Swasey and E. G. Gwinn, J. Phys. Chem. Lett., 2016, 7, 698–703.
13. S. M. Copp, D. Schultz, S. M. Swasey, A. Faris and E. G. Gwinn, Nano Lett., 2016, 16, 3594–3599.
14. E. Thyrhaug, S. A. Bogh, M. R. Carro-Temboury, C. S. Madsen, T. Vosch and D. Zigmantas, Nat. Commun., 2017, 8, 15577.
15. H.-C. Hsu, M.-C. Ho, K.-H. Wang, Y.-F. Hsu and C.-W. Chang, New J. Chem., 2015, 39, 2140–2145.
16. K.-H. Wang and C.-W. Chang, Phys. Chem. Chem. Phys., 2015, 17, 23140–23146.
17. H.-C. Hsu, Y.-X. Lin and C.-W. Chang, Dyes Pigm., 2017, 146, 420–424.
18. S. A. Bogh, C. Cerretani, L. Kacenauskaite, M. R. Carro-Temboury and T. Vosch, ACS Omega, 2017, 2, 4657–4664.
19. M. R. Carro Temboury, V. Paolucci, E. N. Hooley, L. Latterini and T. Vosch, Analyst, 2016, 141, 123–130.
20. D. Jaque and F. Vetrone, Nanoscale, 2012, 4, 4301–4326.
21. K. Okabe, N. Inada, C. Gota, Y. Harada, T. Funatsu and S. Uchiyama, Nat. Commun., 2012, 3, 705.
22. S. Ebrahimi, Y. Akhlaghi, M. Kompany-Zareh and Å. Rinnan, ACS Nano, 2014, 8, 10372–10382.
23. D. Schultz, K. Gardner, S. S. R. Oemrawsingh, N. Markešević, K. Olsson, M. Debord, D. Bouwmeester and E. Gwinn, Adv. Mater., 2013, 25, 2797–2803.
24. C. Würth, M. Grabolle, J. Pauli, M. Spieles and U. Resch-Genger, Nat. Protoc., 2013, 8, 1535–1550.
25. J. R. Lakowicz, Principles of Fluorescence Spectroscopy, Springer, 3rd edn, 2006.
26. S. A. Patel, M. Cozzuol, J. M. Hales, C. I. Richards, M. Sartin, J. C. Hsiang, T. Vosch, J. W. Perry and R. M. Dickson, J. Phys. Chem. C, 2009, 113, 20264–20270.
27. S. H. Yau, N. Abeyasinghe, M. Orr, L. Upton, O. Varnavski, J. H. Werner, H. C. Yeh, J. Sharma, A. P. Shreve, J. S. Martinez and T. Goodson, Nanoscale, 2012, 4, 4247–4254.
28. Usually this is done for fluorophores that decay mono-exponentially, but here we have assumed that the average decay can also be a representative value.
29. S. Choi, R. M. Dickson and J. Yu, Chem. Soc. Rev., 2012, 41, 1867–1891.
30. S. J. Strickler and R. A. Berg, J. Chem. Phys., 1962, 37, 814–822.
31. C. D. S. Brites, P. P. Lima, N. J. O. Silva, A. Millan, V. S. Amaral, F. Palacio and L. D. Carlos, Nanoscale, 2012, 4, 4799–4829.

---

Footnote

† Electronic supplementary information (ESI) available: Materials and methods section, analysis and scenario details, HPLC traces, steady state absorption and emission data, time resolved emission data. See DOI: 10.1039/c7cc06785b

---