Slow magnetic relaxation in five-coordinate spin-crossover cobalt(ii) complexes†
Abstract
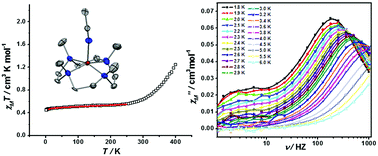
We present the first examples of the coexistence of field induced slow magnetic relaxation and spin-crossover observed in five-coordinate cobalt(II) complexes [Co(12-TMC)(CH3CN)](X)2 (12-TMC = 1,4,7,10-tetramethyl-1,4,7,10-tetraazacyclododecane, X = BF4−, 1; PF6−, 2). The direct-current (dc) magnetic data show a gradual and incomplete spin-crossover at high temperature. 1 and 2 display frequency- and temperature-dependent alternating-current (ac) magnetic susceptibility under an applied dc field of 2500 Oe, which originates from the S = 1/2 spin state of Co(II) ions.


 Please wait while we load your content...
Please wait while we load your content...