Desorption dynamics of CO₂ from formate decomposition on Cu(111)

Abstract

We performed ab initio molecular dynamics analysis of formate decomposition to CO₂ and H on a Cu(111) surface using van der Waals density functionals. Our analysis shows that the desorbed CO₂ has approximately twice larger bending vibrational energy than the translational, rotational, and stretching vibrational energies. Since formate synthesis, the reverse reaction of formate decomposition, has been suggested experimentally to occur via the Eley–Rideal mechanism, our results indicate that the formate synthesis can be enhanced if the bending vibrational mode of CO₂ is excited rather than the translational and/or stretching vibrational modes. Detailed information on the energy distribution of desorbed CO₂ as a formate decomposition product may provide new insights for improving the catalytic activity of formate synthesis.

---

One of the most important intermediate steps in the methanol synthesis over Cu-based catalysts is CO₂ hydrogenation into formate (HCOO).^1–5 Based on a kinetics analysis, it was clarified that formate synthesis is structure insensitive and consistent with an Eley–Rideal (ER) type mechanism.^6–9 Recently, theoretical investigations also suggested the ER and hot atom (HA) mechanisms during CO₂ reduction into formate and/or hydrocarboxyl (HOCO).¹⁰ The ER type mechanism suggests that the formate synthesis can be enhanced by controlling the translational, vibrational, and rotational energies of impinging CO₂. The initial impinging CO₂ energies must be related to the energy states of desorbed CO₂ from formate decomposition because formate synthesis and decomposition are reverse reactions. Therefore, the elucidation of formate decomposition dynamics is important for improving catalytic formate synthesis.

Very recently, the dynamics of desorbed CO₂ produced from the formate decomposition reaction has been studied by measuring the angle-resolved intensity and translational energy distribution of the steady-state reaction of formic acid (HCOOH) and oxygen on a Cu surface.¹¹ It was reported that the translational energy of desorbed CO₂ is approximately 0.10 eV and independent of the surface temperature. The measured CO₂ translational energy is much smaller than the activation energy of formate synthesis, which is 0.59 ± 0.05 eV.^7–9 This suggests that internal modes, such as vibrational and rotational modes, should be excited in the desorbed CO₂. In this study, we therefore investigate the energy distribution of desorbed CO₂ as a formate decomposition product by means of ab initio calculations. We also show the importance of the van der Waals (vdW) interaction in determining the energetics of desorbed CO₂. From the knowledge of desorbing product dynamics, we can deduce optimal conditions for the formate synthesis reaction through CO₂ hydrogenation.

The calculations were performed using a plane-wave pseudopotential code named “Simulation tool for Atom TEchnology (STATE)”.¹² Since the vdW interaction is important to describe the adsorption and chemical reaction of inert molecules,¹³ we compare the Perdew–Burke–Ernzerhof (PBE) results with those obtained using vdW density functionals (vdW-DFs), i.e., the original vdW-DF (vdW-DF1),¹⁴ optB86b-vdW,¹⁵ and rev-vdW-DF2¹⁶ functionals as implemented in the STATE code.¹⁷ We also included the dispersion correction proposed by Grimme with PBE (PBE-D2).¹⁸ We performed ab initio molecular dynamics (AIMD) simulations starting from the transition state (TS) structure of the formate decomposition process to gas phase CO₂ and adsorbed H to evaluate the translational and internal (rotational and vibrational) energies of desorbed CO₂. We have also considered additional samples of the initial geometry for AIMD simulations. We displaced the atoms at the TS towards the second, third, fourth, fifth, and sixth lowest normal mode vectors in such a way that the energies of the displaced geometries are increased from the energy of the TS by 0.02 eV. In the AIMD simulations, the initial velocities are given randomly and they are scaled to set the average kinetic energy of 300 K. Here, we do not include the zero-point energy in the sampling of initial conditions. The detailed calculation methods are provided in the ESI.†

We first calculated the minimum energy path of CO₂ hydrogenation into bidentate formate (bi-HCOO) through monodentate formate (m-HCOO) on Cu(111). The bidentate formate has been observed experimentally as an abundant product during CO₂ hydrogenation compared with its isomer (hydrocarboxyl (HOCO)).^7–9 Moreover, we have also performed the calculations of HOCO adsorption on Cu(111) and found that this species is 0.89 eV less stable using one of the vdW-DFs (optB86b-vdW). Fig. 1 and Table 1 show the energy profile of CO₂ hydrogenation into formate and its detailed descriptions, respectively. As shown in Fig. 1, the hydrogen chemisorption energies (the energy levels of CO₂(g) + 1/2H₂(g)) are quite similar among all functionals except vdW-DF1. On the other hand, the physisorption energies of CO₂ (the energy levels of CO₂(phys) + H*), the energies of the TSs, m-HCOO*, and bi-HCOO* are stabilized through the vdW attraction by approximately 0.13–0.37 eV relative to the PBE result. We then consider the activation energy of formate synthesis (E_a(syn)) as the energy difference between the TS and the CO₂(g) + H* state. This definition of E_a(syn) should correspond to the experimentally observed activation energy of formate synthesis, in which formate was synthesized at a temperature of 333–353 K under atmospheric pressure.⁷ Under these conditions, the hydrogen coverage is close to the saturation point, while CO₂ coverage is almost negligible due to a small adsorption energy. The activation energy of formate decomposition (E_a(dec)) is defined as the energy difference between the TS and bi-HCOO*. As shown in Table 1, only PBE overestimates the experimental E_a(syn), while each functional with a vdW interaction gives a reasonably good result. Meanwhile, each calculated E_a(dec) is in good agreement with the experimental results.

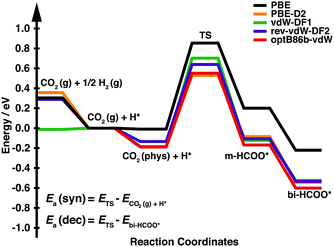Fig. 1 Energy profile for CO₂ hydrogenation to bidentate formate on Cu(111). The energy zero is the sum of the total energies of gas phase CO₂ and an adsorbed hydrogen on the surface (CO₂(g) + H*).

Table 1 Detailed descriptions of the energy profile of CO₂ hydrogenation into formate (in eV) on Cu(111), and calculated formate synthesis and decomposition energies using PBE, PBE-D2, and vdW-DFs. The values in brackets were obtained using a six layer-thick slab. The zero-point energy (ZPE) correction is evaluated using the optB86b-vdW functional

	This study					Expt.
	PBE	PBE-D2	vdW-DF1	rev-vdW-DF2	optB86b-vdW
a Taken from ref. 7. b Taken from ref. 8 and 9.
E CO2(g) + 1/2H2(g)	+0.30 (+0.22)	+0.36	−0.01	+0.29	+0.30 (+0.22)	—
E CO2(phys) + H*	−0.01 (−0.01)	−0.19	−0.18	−0.13	−0.19 (−0.18)	—
E TS	+0.85 (+0.78)	+0.53	+0.70	+0.64	+0.55 (+0.52)	—
E m-HCOO*	+0.20 (+0.17)	−0.08	−0.12	−0.11	−0.17 (−0.18)	—
E bi-HCOO*	−0.22 (−0.33)	−0.54	−0.52	−0.53	−0.60 (−0.70)	—
E a(syn)	0.85 (0.78)	0.53	0.70	0.64	0.55 (0.52)
E a(syn) + ZPE	0.80 (0.73)	0.48	0.65	0.59	0.50 (0.47)	0.59 ± 0.05^a
						0.66 ± 0.02^b
E a(dec)	1.08 (1.12)	1.07	1.23	1.17	1.15 (1.22)
E a(dec) + ZPE	0.90 (0.94)	0.89	1.05	0.99	0.97 (1.04)	1.12 ± 0.03^a
						1.17 ± 0.13^b

---

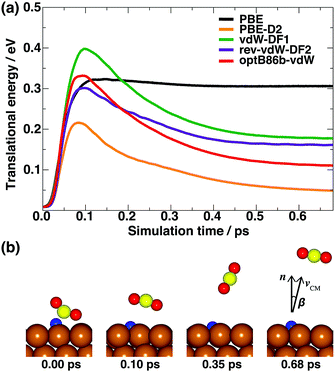
Next, we explored the energy distribution of desorbed CO₂ as a product of formate decomposition. We calculated the CO₂ translational energy (E_t) from the velocity of the center of mass of CO₂. Fig. 2a summarizes the time evolution of CO₂ translational energy. The representative snapshots of CO₂ desorption from the AIMD trajectory are shown in Fig. 2b. There are significant differences in the E_t profiles calculated using PBE and those using PBE-D2 and vdW-DFs. Here, PBE predicts a constant E_t value at 0.30 eV after the CO₂ molecule experiences Pauli repulsion in the first 0.10 ps (shown as a black line in Fig. 2a). Meanwhile, the PBE-D2 and vdW-DFs show different time evolution profiles of the CO₂ translational energy. In the first 0.08–0.10 ps, the E_t value increases to 0.20–0.32 eV due to the Pauli repulsion between CO₂ and the surface. Then, it decreases gradually to a certain value. The decrease in the CO₂ translational energy is due to the vdW attraction between CO₂ and the Cu(111) surface. We also estimated the desorption angle (β) of CO₂ at 0.68 ps, when it already has a constant E_t value, from the direction of the velocity of center of mass relative to the surface normal (Fig. 2b). The calculated β using PBE, PBE-D2, vdW-DF1, rev-vdW-DF2, and optB86b-vdW are 5°, 18°, 8°, 12°, and 14°, respectively, in which the angular distribution of desorbed CO₂ shows quite sharp collimation along the surface normal direction and is in good agreement with the experimental results.¹¹ As summarized in Table 2, the calculated E_t values using PBE-D2 and vdW-DFs are in reasonable agreement with the experimental estimation,¹¹ while PBE fails in predicting this energy. Therefore, the vdW interaction is important for describing the translational energy of desorbed CO₂.

Table 2 Calculated translational energy (E_t), rotational energy (E_r), vibrational energy of the bending mode (E_b), and vibrational energy of the symmetric stretching mode (E_s) of desorbed CO₂ from formate decomposition on Cu(111) using PBE, PBE-D2, and vdW-DFs (in eV). The calculation results using the optB86b-vdW functional are the average results from several samples of AIMD trajectory

	This study					Expt.^a
	PBE	PBE-D2	vdW-DF1	rev-vdW-DF2	optB86b-vdW
a Experimentally measured CO2 translational energy as a formate decomposition product taken from ref. 11. b This energy is deduced from: Ea(syn) − (Et + Er + Eb + Es).
E t	0.30	0.05	0.18	0.16	0.14 ± 0.03	0.10
E r	0.08	0.09	0.08	0.11	0.11 ± 0.03	—
E b	0.27	0.24	0.25	0.26	0.26 ± 0.02	—
E s	0.06	0.05	0.10	0.08	0.04 ± 0.02	—
Surface mode^b	0.14	0.10	0.09	0.03	0.03 ± 0.02	—

---

Fig. 2 (a) Time evolution of the translational energy of desorbed CO₂ from formate decomposition calculated using PBE, PBE-D2, and vdW-DFs. (b) Representative snapshots from the AIMD trajectory of CO₂ desorption. n and v_CM represent the direction of the surface normal and the velocity of the center of mass of CO₂, respectively.

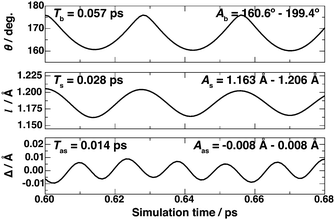
We also evaluated the energy transfer by formate decomposition into the internal modes (rotational and vibrational) of CO₂. The rotational energy (E_r) of CO₂ as a function of time was calculated from the moment of inertia of CO₂ and its angular momentum at each time step of the MD trajectory. Table 2 shows that the calculated E_r value varies in between 0.08 and 0.11 eV. The CO₂ bending, symmetric stretching, antisymmetric stretching vibrational energies are evaluated based on the time evolution of the desorbed CO₂ geometry, i.e., bond angle (θ), the C–O bond length (l), and the difference between two C–O bond lengths (Δ), respectively, as shown in Fig. 3. For comparison, we also evaluated the vibrational frequencies of an isolated CO₂ (see the ESI†). The calculated zero-point energies of isolated CO₂ bending, symmetric stretching, and antisymmetric stretching vibrational modes using optB86b-vdW are 76.72 meV, 164.61 meV, and 295.74 meV, respectively, which are in good agreement with the experimental values of 82.70 meV, 165.27 meV, and 291.24 meV, respectively.^19,20 These calculated zero-point energies are nearly independent of the functional. The vibrational energy of the bending mode (E_b ∼ 0.25 eV) of desorbed CO₂ is close to the third excitation of the zero-point energy of isolated CO₂. All functionals produce similar E_b values in the range of 0.24–0.26 eV. The calculated vibrational energy of the CO₂ symmetric mode (E_s) varies between 0.05 and 0.11 eV, which is close to the zero-point energy of the isolated CO₂ symmetric mode. Meanwhile, the vibrational energy of the antisymmetric mode (E_as ∼ 1.5 meV) is much smaller than the zero-point energy of isolated CO₂.

Fig. 3 Time evolution of the CO₂ bond angle (θ), the C–O bond length (l), and the difference between two C–O bond lengths (Δ) based on the AIMD trajectory calculated using the optB86b-vdW functional. The period (T) and amplitude (A) of each geometry data are shown in each panel.

Based on our calculations, nearly a half of E_a(syn) is transferred into the CO₂ bending mode, a quarter into each translational and rotational modes, and rather a small energy is transferred into the CO₂ stretching modes. The origin for the strong enhancement of the CO₂ bending mode can be ascribed to its geometry at the TS, in which the CO₂ bond angle is nearly 140°. The rest of E_a(syn) may have transferred into the surface modes, namely, hydrogen–Cu and/or Cu–Cu vibrations. We also performed the sudden vector projection (SVP) analysis proposed by Jiang and Guo.²¹ We showed that the SVP analysis qualitatively agrees rather well with our AIMD simulation results (shown in the ESI†). Therefore, our results strongly suggest that formate synthesis, the reverse process of the formate decomposition, can be enhanced by increasing the vibrational energy of the CO₂ bending mode.

The present results are in sharp contrast to the case of CO₂ dissociation, in which the CO₂ symmetric and antisymmetric stretching modes are theoretically suggested to be more important to increase the dissociation rate.²² The importance of stretching modes in the CO₂ dissociation was implied experimentally in the study of CO₂ dynamics from CO oxidation on Pd surfaces.^23–25 The desorbed CO₂ has 0.12–0.16 eV in the vibrational energy of the antisymmetric mode, which is slightly larger than the vibrational energy of the CO₂ symmetric-bending mode (0.11–0.13 eV). Moreover, the measured translational (0.10–0.12 eV)²⁶ and rotational (0.08–0.10 eV)^23,25,27,28 energies of desorbed CO₂ from CO oxidation on Pd surfaces are smaller than its vibrational energy of the antisymmetric mode. Therefore, CO₂ dissociation can be selectively enhanced by exciting the CO₂ stretching vibrational modes.

Finally, we discuss the temperature dependence of the translational energy of CO₂. Experimentally, it was reported that E_t of desorbed CO₂ from formate decomposition is independent of the surface temperature,¹¹ while that from CO oxidation is linearly dependent on the surface temperature.²⁶ From our theoretical simulations, it turns out that at most 20% of E_a(syn) is transferred into surface modes. On the other hand, it can be deduced that approximately 60% of the activation energy of CO₂ dissociation (1.30 eV)²⁹ on a Pd surface, which is a reverse reaction of CO oxidation, is transferred to the surface mode. Both results, namely, the surface temperature dependence and the energy transfer to the surface mode, indicate the strength of the coupling between CO₂ and the surfaces at the TS of reactions. In the case of formate decomposition, CO₂ is weakly bonded as seen in the left panel of Fig. 2b. This is in contrast to the case of CO oxidation, where CO₂ was found to spend a significant residence time in the chemisorption well before it desorbs.³⁰ Moreover, one of the two C–O bond lengths of CO₂ is significantly elongated at the TS of CO oxidation, and carbon and oxygen are strongly bonded to the surface.³¹

In summary, we have investigated the minimum energy path of CO₂ hydrogenation into formate and the dynamics of formate decomposition into gas phase CO₂ and adsorbed hydrogen using density functional theory calculations. Based on the dynamics analysis of formate decomposition, the bending energy of desorbed CO₂ is twice larger than the translational energy. Since formate synthesis from CO₂ and H₂, the reverse reaction of the formate decomposition, is experimentally suggested to occur via the ER type mechanism, our results indicate that the reaction rate of formate synthesis can be enhanced if the bending vibrational mode of CO₂ is excited rather than the translational and/or stretching modes. Meanwhile, these results are quite different from the case of CO₂ dissociation, in which the antisymmetric stretching mode is the key to increasing the dissociation rate. Accordingly, we anticipate that this work may contribute to the future development in controlling the particular molecular vibrational mode for improving catalytic reactions.

The authors thank Prof. Junji Nakamura, Prof. Takahiro Kondo, and Dr Jiamei Quan for their valuable discussions. The present work was supported by the Advanced Catalytic Transformation Program for Carbon utilization (ACT-C) (Grant No. JPMJCR12YU) of the Japan Science and Technology Agency (JST), and partly supported by Grants-in Aid for Scientific Research on Innovative Areas 3D Active-Site Science (No. 26105010 and No. 26105011) from the Japan Society for the Promotion of Science (JSPS) and the Elements Strategy Initiative for Catalysts and Batteries (ESICB) supported by the Ministry of Education, Culture, Sports, Science, and Technology, Japan (MEXT). The numerical calculations were performed using the computer resources at the Institute for Solid State Physics (ISSP), Univ. of Tokyo, and the HPCI systems provided by Nagoya Univ., Univ. of Tokyo, and Tohoku Univ. through the HPCI System Research Project (Project ID: hp130112, hp140166, and hp150201).

References

1. S. Kattel, P. J. Ramrez, J. G. Chen, J. A. Rodriguez and P. Liu, Science, 2017, 355, 1296–1299.
2. S. Kuld, M. Thorhauge, H. Falsig, C. F. Elkjær, S. Helveg, I. Chorkendorff and J. Sehested, Science, 2016, 352, 969–974.
3. M. Behrens, F. Studt, I. Kasatkin, S. Kühl, M. Hävecker, F. Abild-Pedersen, S. Zander, F. Girgsdies, P. Kurr, B.-L. Kniep, M. Tovar, R. W. Fischer, J. K. Nørskov and R. Schlögl, Science, 2012, 336, 893–897.
4. L. C. Grabow and M. Mavrikakis, ACS Catal., 2011, 1, 365–384.
5. T. Fujitani, I. Nakamura, T. Uchijima and J. Nakamura, Surf. Sci., 1997, 383, 285–298.
6. G. Wang, Y. Morikawa, T. Matsumoto and J. Nakamura, J. Phys. Chem. B, 2006, 110, 9–11.
7. H. Nakano, I. Nakamura, T. Fujitani and J. Nakamura, J. Phys. Chem. B, 2001, 105, 1355–1365.
8. H. Nishimura, T. Yatsu, T. Fujitani, T. Uchijima and J. Nakamura, J. Mol. Catal. A: Chem., 2000, 155, 3–11.
9. I. Nakamura, H. Nakano, T. Fujitani, T. Uchijima and J. Nakamura, J. Vac. Sci. Technol., A, 1999, 17, 1592–1595.
10. W. Lin, K. M. Stocker and G. C. Schatz, J. Am. Chem. Soc., 2017, 139, 4663–4666.
11. J. Quan, T. Kondo, G. Wang and J. Nakamura, Angew. Chem., Int. Ed., 2017, 56, 3496–3500.
12. Y. Morikawa, K. Iwata, J. Nakamura, T. Fujitani and K. Terakura, Chem. Phys. Lett., 1999, 304, 91–97.
13. F. Nattino, D. Migliorini, M. Bonfanti and G.-J. Kroes, J. Chem. Phys., 2016, 144, 044702.
14. M. Dion, H. Rydberg, E. Schröder, D. C. Langreth and B. I. Lundqvist, Phys. Rev. Lett., 2004, 92, 246401.
15. J. Klimeš, D. R. Bowler and A. Michaelides, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83, 195131.
16. I. Hamada, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 89, 121103.
17. Y. Hamamoto, I. Hamada, K. Inagaki and Y. Morikawa, Phys. Rev. B, 2016, 93, 245440.
18. S. Grimme, J. Comput. Chem., 2006, 27, 1787–1799.
19. T. Shimanouchi, Tables of Molecular Vibrational Frequencies, Consolidated Volume 1, National Standard Reference Data System (NSRDS), Tokyo, Japan, 1972.
20. W. B. Person and G. Zerbi, Vibrational intensities in infrared and Raman spectroscopy, Elsevier Scientific Pub. Co., Amsterdam, Netherland, 1982.
21. B. Jiang and H. Guo, J. Chem. Phys., 2013, 138, 234104.
22. B. Jiang and H. Guo, J. Chem. Phys., 2016, 144, 091101.
23. T. Yamanaka, Phys. Chem. Chem. Phys., 2008, 10, 5429–5435.
24. K. Nakao, S. Ito, K. Tomishige and K. Kunimori, Catal. Today, 2006, 111, 316–321.
25. K. Nakao, S. Ito, K. Tomishige and K. Kunimori, J. Phys. Chem. B, 2005, 109, 17553–17559.
26. K. Kimura, Y. Ohno and T. Matsushima, Surf. Sci., 1999, 429, L455–L461.
27. H. Uetsuka, K. Watanabe, H. Ohnuma and K. Kunimori, Surf. Sci., 1997, 377, 765–769.
28. H. Uetsuka, K. Watanabe and K. Kunimori, Surf. Sci., 1996, 363, 73–78.
29. T. Engel and G. Ertl, J. Chem. Phys., 1978, 69, 1267–1281.
30. X. Zhou, B. Kolb, X. Luo, H. Guo and B. Jiang, J. Phys. Chem. C, 2017, 121, 5594–5602.
31. A. Alavi, P. Hu, T. Deutsch, P. L. Silvestrelli and J. Hutter, Phys. Rev. Lett., 1998, 80, 3650–3653.

---

Footnote

† Electronic supplementary information (ESI) available: Additional information. See DOI: 10.1039/c7cc03707d

---