Combined measurement of directional Raman scattering and surface-plasmon-polariton cone from adsorbates on smooth planar gold surfaces†
Abstract
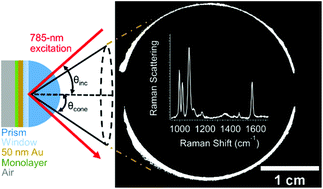
Directional-surface-plasmon-coupled Raman scattering (directional RS) has the combined benefits of surface plasmon resonance and Raman spectroscopy, and provides the ability to measure adsorption and monolayer-sensitive chemical information. Directional RS is performed by optically coupling a 50 nm gold film to a Weierstrass prism in the Kretschmann configuration and scanning the angle of the incident laser under total internal reflection. The collected parameters on the prism side of the interface include a full surface-plasmon-polariton cone and the full Raman signal radiating from the cone as a function of incident angle. An instrument for performing directional RS and a quantitative study of the instrumental parameters are herein reported. To test the sensitivity and quantify the instrument parameters, self-assembled monolayers and 10 to 100 nm polymer films are studied. The signals are found to be well-modeled by two calculated angle-dependent parameters: three-dimensional finite-difference time-domain calculations of the electric field generated in the sample layer and projected to the far-field, and Fresnel calculations of the reflected light intensity. This is the first report of the quantitative study of the full surface-plasmon-polariton cone intensity, cone diameter, and directional Raman signal as a function of incident angle. We propose that directional RS is a viable alternative to surface plasmon resonance when added chemical information is beneficial.


 Please wait while we load your content...
Please wait while we load your content...