Solvent vapor annealing in block copolymer nanocomposite films: a dynamic mean field approach†
Huikuan
Chao
,
Jason
Koski
and
Robert A.
Riggleman
*
Chemical and Biomolecular Engineering, University of Pennsylvania, Philadelphia, PA 19104, USA. E-mail: rrig@seas.upenn.edu
First published on 6th June 2016
Abstract
Polymer nanocomposites are an important class of materials due to the nanoparticles' ability to impart functionality not commonly found in a polymer matrix, such as electrical conductivity or tunable optical properties. While the equilibrium properties of polymer nanocomposites can be treated using numerous theoretical and simulation approaches, in experiments the effects of processing and kinetic traps are significant and thus critical for understanding the structure and the functionality of polymer nanocomposites. However, simulation methods that can efficiently predict kinetically trapped and metastable structures of polymer nanocomposites are currently not common. This is particularly important in inhomogeneous polymers such as block copolymers, where techniques such as solvent vapor annealing are commonly employed to improve the long-range order. In this work, we introduce a dynamic mean field theory that is capable of predicting the result of processing the structure of polymer nanocomposites, and we demonstrate that our method accurately predicts the equilibrium properties of a model system more efficiently than a particle-based model. We subsequently use our method to predict the structure of block copolymer thin films with grafted nanoparticles after solvent annealing, where we find that the final distribution of the grafted nanoparticles can be controlled by varying the solvent evaporation rate. The extent to which the solvent evaporation rate can affect the final nanoparticle distribution in the film depends on the grafting density and the length of the grafted chains. Furthermore, the effects of the solvent evaporation rate can be anticipated from the equilibrium nanoparticle distribution in the swollen and dry states.
Introduction
Inhomogeneous polymeric materials have witnessed exciting developments and promising commercial benefits in the past several decades. The inhomogeneity can arise from either macroscopic phase separation or microscopic ordered structures, which enables the broad applications, including the usage of block copolymers in nanolithography,1,2 adhesives,3 and cosmetic and ultrafiltration products.4 As a result of the relatively weak interactions (typically a few kT), many experimental and industrially relevant processes generally involve kinetic processing, where the final states of the material are highly sensitive to the processing conditions. During processing, the evolution of the structure is strongly coupled with the dynamics of constituent polymers and solvents. For example, rapid solvent evaporation is commonly used in experiments of microphase separated block copolymer thin films to obtain specific ordered structures.5–7 The resultant copolymer morphology after processing is found to depend on the solvent evaporation speed and copolymer composition.8–11The situation becomes even more complicated when we consider polymer nanocomposites (PNCs), an important class of polymeric materials where nanoparticles are added to the polymer matrix. The nanoparticles have the ability to confer the polymers with novel properties including enhanced mechanical properties,12–15 tunable optical features16–18 and conductive pathways.19 It is found that these material properties are dictated by both the equilibrium20–22 and nonequilibrium13,23,24 nanoparticle distributions and thus the ability to accurately and efficiently control the nanoparticle distributions a priori becomes a large design challenge for PNCs. The distribution of nanoparticles in polymer matrices is also dictated by the interplay between the dynamics of polymers and the mobility of nanoparticles, which is controlled by the nanoparticle geometry, the surface chemistry and the matrix polymer size.25,26 Although widely studied for neat block copolymer films,8 solvent annealing strategies for controlling the distribution of nanoparticles in block copolymer films have received significantly less attention. Given all the aforementioned importance of kinetics and processing on the performance and the self-assembly of inhomogeneous polymeric materials, it is important to develop both simulation and theoretical tools that are capable of elucidating both the equilibrium and nonequilibrium structure and properties of not only polymer materials, but also soft matter systems in general.
At equilibrium, field-theoretic simulations (FTSs) have played an important role in our understanding of inhomogeneous soft matter systems, particularly in polymeric materials.27,28 The approach begins with a coarse-grained model of the system, where polymers are typically modeled as Gaussian chains and relatively simple non-bonded interactions such as Flory-like repulsions between dissimilar components or Coulombic interactions.29,30 Then using any of a variety of analytic techniques,27,31,32 the coarse-grained model can be exactly transformed to a field-theoretic model where one must calculate the interactions of single molecules with the chemical potential fields generated by the remaining molecules. The particle-to-field transformation is frequently followed by a mean-field approximation, which enables the rapid generation of phase diagrams for a variety of systems, though techniques have emerged in recent years to avoid this approximation.27,33,34 Polymer nanocomposites have been studied using field-theoretic approaches by performing either hybrid SCFT/particle simulations35–37 or SCFT-DFT calculations,38–41 though these methods relied on the mean field approximation.
Recently we extended the polymer field theory framework to allow simulations of polymer nanocomposites by showing how to take the same models used in the hybrid particle field theory approach and trace them through the particle-to-field transformation to generate a polymer nanocomposite field theory (PNC-FT) that is amenable to sampling the fluctuating fields using techniques such as complex Langevin sampling.22,42,43 By giving the polymer monomers and the nanoparticles a finite size and shape, we effectively replace the delta function densities and interactions commonly used in FTS with finite-range interactions,42,44 which in turn give rise to important physics such as particle correlations. To date, applications of this framework have been limited to equilibrium calculations,43,45 and the goal of this paper is to present an efficient method that enables non-equilibrium calculations using the same family of models.
There are numerous approaches for taking field theoretic simulations out of equilibrium. The most common approach is the dynamic SCFT method first developed by Fraaije;46 in this approach, the dynamics of density fields are evolved according to a generalized diffusion equation that involves a non-local Onsager coefficient rather than a simple diffusion coefficient. All of the essential physics of the dynamical process are buried into the Onsager coefficient, and since more realistic models for the Onsager coefficient are frequently difficult to derive and evaluate efficiently, these coefficients are often replaced with simple monomer diffusion coefficients. Furthermore, this approach typically relies on an equilibrium expression for the free energy F, and deriving a closed form from a field theory requires either the mean-field approximation or other more severe approximations. The so-called two fluid formalism has also been successfully used to predict the dynamics of polymer solutions and blends,47,48 though again it requires the use of the equilibrium free energy expression. More than a decade ago Fredrickson showed how to generalize this framework beyond the mean-field approximation,49 but this approach has seen little development because it is computationally demanding50 and strategies for efficiently solving the equations do not yet exist. Similarly, the hydrodynamic self-consistent field theory (HSCFT) is unique in that it is one of the relatively few field theoretic simulation approaches that has been employed in situations beyond equilibrium for both phase separated block copolymers and nanocomposite materials,51,52 but again this method typically relies on the mean-field approximation, is computationally demanding, and requires the input of a constitutive law to couple the local stress to the local density fields.
Very recently, Fredrickson and Orland53 (FO) and separately Grzetic, Wickham, and Shi54 (GWS) developed a dynamic mean-field theory that begins from a formally exact classical path integral description of the dynamics55–57 in the spirit of the Martin–Siggia–Rose (MSR) approach. After performing particle-to-field transformations akin to those commonly used in the development of equilibrium polymer field theories27 and invoking a dynamic mean-field approximation, they arrived at a set of equations where independent polymer chains evolve in time due to non-bonded forces generated by a continuous density field. While GWS then numerically solved the equations for a simple fluid, FO showed how using this framework, one can derive the self-consistent Brownian dynamics (SCBD),58,59 single-chain in mean-field (SCMF),60,61 and related approaches that evolve independent chains in potential fields generated by the surrounding chains. The advantage of this approach is that the equations are systematically derived from an exact representation of the model's dynamics, allowing for the possibility of developing more sophisticated dynamic mean field theories that include more complex intermolecular interactions or incorporate hydrodynamic interactions.62
In this study, we implement the dynamic mean field theory (DMFT) recently proposed by Fredrickson and Orland,53 and extend it to the polymer nanocomposite models used in the PNC-FT and hybrid particle–field theory. For a Gaussian regularized Edwards model44 of a homopolymer in an implicit solvent, we show that the method quantitatively reproduces thermodynamic properties calculated directly from the equivalent particle-based model using dissipative particle dynamics (DPD) and complex Langevin field theoretic simulations (CL-FTSs) of the same system. Our implementation of the DMFT method is shown to be faster than DPD simulations of the same systems, and the DMFT approach scales more efficiently with polymer chain density, C. We then use this method to study solvent vapor annealing in block copolymer nanocomposite thin films. The addition of solvent can be used to modify the equilibrium distribution of nanoparticles in the swollen film compared to the dry film depending on the grafting density, the grafted chain length, and the nanoparticle concentration. This change in the equilibrium distribution of nanoparticles throughout the film can then be exploited to control the final distribution of nanoparticles after solvent annealing by varying the solvent evaporation rate. When the solvent evaporates rapidly so that the film contraction rate is larger than the nanoparticle diffusion time, the particles remain trapped in their distribution in the swollen state. However, when the solvent evaporation rate is slow, the nanoparticles can anneal to their equilibrium, dry film configuration.
Theory and implementation
We work with two systems in this work: a homopolymer in an implicit solvent (a version of the canonical Edwards model) and a block copolymer thin film that undergoes solvent annealing. In this section, we describe the details of both models. First, we use the simpler Edwards model to describe the key details of the DMFT framework, and we subsequently describe the relevant details for the block copolymer thin film system.Homopolymer in an implicit solvent
We work with a Gaussian regularized version of the Edwards model of a homopolymer in an implicit solvent that is free of ultraviolet divergences.29,44 Our system contains n polymer chains that are modeled as discrete Gaussian chains with N interaction sites per chain, and all monomers interact through a Gaussian pair potential of the form| uG(rij) = u0(2πb2)−d/2e−|rij|2/2b2, | (1) |
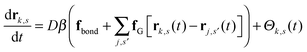 | (2) |
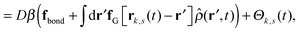 | (3) |
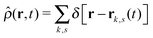 is the total segment density, and Θk,s(t) is a vector of independent Gaussian random variables, where each component α obeys the statistics
is the total segment density, and Θk,s(t) is a vector of independent Gaussian random variables, where each component α obeys the statistics| 〈Θk,α(s,t)〉 = 0, | (4) |
| 〈Θk,α(s,t)Θm,β(s′,t′)〉 = 2Dδk,mδs,s′δ(t − t′)δα,β. | (5) |
Our derivation of the dynamic mean field theory (DMFT) closely follows that of the work of Fredrickson and Orland,53 so we only reproduce the main details here. The starting point to derive the mean field theory is a time-sliced path integral representation of the dynamics of the polymer chains. The dynamic partition function is given by
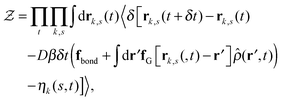 | (6) |
 in eqn (6), the path integrals
in eqn (6), the path integrals  represent a sum over all possible trajectories of the polymer segment while the delta function selects only those trajectories consistent with the dynamics given by a discretized version of eqn (3). The next steps closely follow a common approach for the development of equilibrium polymer field theories,27 where we insert into
represent a sum over all possible trajectories of the polymer segment while the delta function selects only those trajectories consistent with the dynamics given by a discretized version of eqn (3). The next steps closely follow a common approach for the development of equilibrium polymer field theories,27 where we insert into 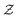 the identity
the identity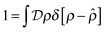 | (7) |
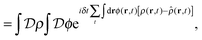 | (8) |
![[small rho, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b7.gif) ], and the second equality follows from the exponential (Fourier) representation of the delta functional. This identity allows the replacement of
], and the second equality follows from the exponential (Fourier) representation of the delta functional. This identity allows the replacement of ![[small rho, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b7.gif) in the equation of motion (eqn (3)) with the continuous density field ρ, which decouples the nonbonded forces between the n polymer chains. Following some rearrangements, we arrive at a dynamic partition function of the form
in the equation of motion (eqn (3)) with the continuous density field ρ, which decouples the nonbonded forces between the n polymer chains. Following some rearrangements, we arrive at a dynamic partition function of the form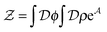 | (9) |
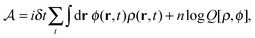 | (10) |
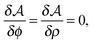 | (11) |
| ϕ(r,t) = 0 | (12) |
ρ(r,t) = 〈![[small rho, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b7.gif) (r,t)〉. (r,t)〉. | (13) |
![[small rho, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b7.gif) (r,t) that are generated from an ensemble of chains that do not directly interact with each other, but only with the continuous density field. This approach is generalized trivially to multi-component systems with several non-bonded interaction potentials.
(r,t) that are generated from an ensemble of chains that do not directly interact with each other, but only with the continuous density field. This approach is generalized trivially to multi-component systems with several non-bonded interaction potentials.
Implementation
In the DMFT method, a collection of molecules with explicit particle coordinates![[small rho, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b7.gif) (r,t) are evolved at each time step according to a discretized equation of motion. Bonded forces arise directly from the molecular configurations, while the nonbonded forces arise from the interactions of the molecules with a continuous density field ρ(r,t); there are no direct intermolecular interactions. At each time step, one begins with a set of (non-interacting) molecular configurations for n chains, which defines the particle density
(r,t) are evolved at each time step according to a discretized equation of motion. Bonded forces arise directly from the molecular configurations, while the nonbonded forces arise from the interactions of the molecules with a continuous density field ρ(r,t); there are no direct intermolecular interactions. At each time step, one begins with a set of (non-interacting) molecular configurations for n chains, which defines the particle density ![[small rho, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b7.gif) (r,t). The continuous density field ρ(r,t) is then defined from the particle density using particle-to-mesh (PM) techniques that are standard tools for PM Ewald summations in particle-based simulations of charged systems.63–66 Next, the nonbonded forces on the mesh f(nb)(r,t) are given as the convolution between the gradient of the nonbonded potential, −∇u(r), and the density field ρ(r,t), which takes the form
(r,t). The continuous density field ρ(r,t) is then defined from the particle density using particle-to-mesh (PM) techniques that are standard tools for PM Ewald summations in particle-based simulations of charged systems.63–66 Next, the nonbonded forces on the mesh f(nb)(r,t) are given as the convolution between the gradient of the nonbonded potential, −∇u(r), and the density field ρ(r,t), which takes the form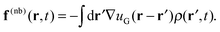 | (14) |
Multi-component systems
In this work, where our ultimate goal is to study solvent annealing in model block copolymer nanocomposites, we implement the form of a polymer nanocomposite model that we have studied extensively in our previous work.22,42,43 We begin with component densities that are written for component I as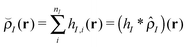 , where hI(r) describes how the mass is distributed around the coarse-grained segment. For polymer monomers, we assume that hI has a Gaussian form, while for nanoparticles hI(r) is a smoothed step function that changes from ρ0 in the particle core to 0 away from the particle surface. The original implementation of the hybrid particle–field theory of Sides and Fredrickson used a similar distribution function for the nanoparticle centers and a delta function distribution for polymer monomers.35
, where hI(r) describes how the mass is distributed around the coarse-grained segment. For polymer monomers, we assume that hI has a Gaussian form, while for nanoparticles hI(r) is a smoothed step function that changes from ρ0 in the particle core to 0 away from the particle surface. The original implementation of the hybrid particle–field theory of Sides and Fredrickson used a similar distribution function for the nanoparticle centers and a delta function distribution for polymer monomers.35
With our densities defined in this manner, we can write a Flory-like potential energy of interaction between components I and J in our system in two equivalent forms:42,44
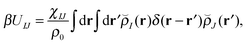 | (15) |
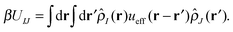 | (16) |
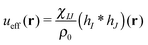 is the effective pair potential between the interaction site centers and * represents a convolution integral. In other words, the effective interaction potential between any two components can be written as a convolution of the two functions describing the shapes of the particles. The first form (eqn (15)) is convenient for field-theoretic simulations, while the second form (eqn (16)) is appropriate for particle-based approaches and the current DMFT approach.
is the effective pair potential between the interaction site centers and * represents a convolution integral. In other words, the effective interaction potential between any two components can be written as a convolution of the two functions describing the shapes of the particles. The first form (eqn (15)) is convenient for field-theoretic simulations, while the second form (eqn (16)) is appropriate for particle-based approaches and the current DMFT approach.
Different components of our system are modeled using different forms for their shape functions, hI(r). For the coarse-grained interaction sites that comprise a polymer chain, we use a unit Gaussian form, hG(r) = (2πa2)−d/2e−|r|2/2a2, where a is taken as a numerical parameter of our simulations. For nanoparticles, we adopt a smoothed step function
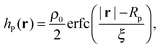 | (17) |
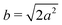 ; the interaction between two nanoparticles is the convolution of the smoothed spherical step function given in eqn (17); and the cross-interaction is given by the convolution of the Gaussian with the smoothed step function. The nonbonded forces are then taken as the gradient of these potentials, which allows us to make direct comparisons between equilibrium field theoretic simulations, particle-based models, and the DMFT implementation all using an identical underlying particle model.
; the interaction between two nanoparticles is the convolution of the smoothed spherical step function given in eqn (17); and the cross-interaction is given by the convolution of the Gaussian with the smoothed step function. The nonbonded forces are then taken as the gradient of these potentials, which allows us to make direct comparisons between equilibrium field theoretic simulations, particle-based models, and the DMFT implementation all using an identical underlying particle model.
Block copolymer nanocomposite films
Our block copolymer nanocomposite systems consist of four chemical components: A–B block copolymers of length N, A-grafted nanoparticles with graft length Ng and nanoparticle cores of type P, the solvent S, which are given the same size as polymer monomers, and a third immiscible homopolymer component C. The non-bonded potential energy used to model the block copolymer nanocomposite films consists of Flory interaction terms between all components plus the Helfand compressibility potential69 that penalizes density fluctuations away from ρ0. The total non-bonded potential energy function is given by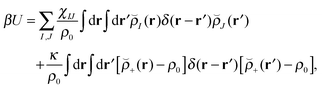 | (18) |
All bonds are harmonic bonds where each pair of monomers s and s + 1 experiences a potential 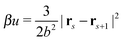 . The graft sites on the surface of the nanoparticles are given a random, fixed distribution, and each particle has a unique distribution of graft sites. The ends of the grafted chains are bonded to the graft sites with the same harmonic potential, and the torque applied to the particle cores through their bonding to the grafted chains causes the particles to rotate. The rotational dynamics of the nanoparticle cores are evolved using a recent quaternion-based rotational Brownian dynamics algorithm,70 and the details of the implementation are given in the ESI.†
. The graft sites on the surface of the nanoparticles are given a random, fixed distribution, and each particle has a unique distribution of graft sites. The ends of the grafted chains are bonded to the graft sites with the same harmonic potential, and the torque applied to the particle cores through their bonding to the grafted chains causes the particles to rotate. The rotational dynamics of the nanoparticle cores are evolved using a recent quaternion-based rotational Brownian dynamics algorithm,70 and the details of the implementation are given in the ESI.†
The confinement of the block copolymer to a film was maintained through the use of a masking function akin to those commonly employed in field theoretic simulations,71 and the substrates were treated as reflecting boundary conditions at the top and bottom of our simulation box. During any time step where a particle would pass through the plane of the substrate, their position was simply reflected into the block copolymer film. To mimic a free surface in our block copolymer film, we follow several previous studies that use an immiscible fluid to maintain the fluid/fluid interface.41,72,73 Here, we use a homopolymer (which we denote as type C) with a degree of polymerization NC = 10, while the block copolymers are discretized into N = 60 interaction sites.
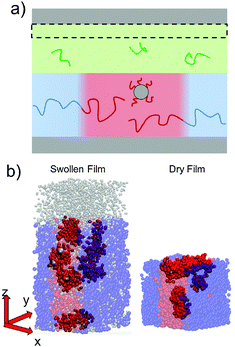
To simulate exposure to solvent, the solvent is added to a region in the C phase whose lower boundary is 2Rg away from the soft interface in the swollen film, where 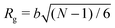 is the polymer radius of gyration; similarly, solvent is removed from the same region during simulated evaporation. We assume that a solvent molecule occupies the same volume as a coarse-grained polymer monomer, and to maintain a constant total density ρ0 solvent is added (or removed) NC molecules at a time, and we remove (or add) a C chain from the region above the block copolymer surface. Fig. 1 shows a schematic of our model system setup. To control the rate of solvent removal, we vary the frequency with which we remove solvent from the simulation box, and the rate is quantified by tracking the height of the block copolymer film as a function of time. We find that the height is approximately linear as a function of time during solvent removal, and we take the slope as the solvent removal rate.
is the polymer radius of gyration; similarly, solvent is removed from the same region during simulated evaporation. We assume that a solvent molecule occupies the same volume as a coarse-grained polymer monomer, and to maintain a constant total density ρ0 solvent is added (or removed) NC molecules at a time, and we remove (or add) a C chain from the region above the block copolymer surface. Fig. 1 shows a schematic of our model system setup. To control the rate of solvent removal, we vary the frequency with which we remove solvent from the simulation box, and the rate is quantified by tracking the height of the block copolymer film as a function of time. We find that the height is approximately linear as a function of time during solvent removal, and we take the slope as the solvent removal rate.
Simulations of a bulk block copolymer were used to determine the equilibrium domain spacing of the grafted nanoparticle/block copolymer composite both in the dry and swollen states. The bulk domain spacings were then used in our thin film simulations, and during the drying procedure we linearly interpolated the domain spacing between the swollen and dry domain spacing by applying a small affine deformation each time solvent was removed from the simulation box.
The solvent and the nanoparticle cores are neutral to all other components (χS* = χP* = 0), and the solvent is added to a maximum volume fraction of ϕS = 0.33. The grafted nanoparticle cores have a diameter of RP = 0.5Rg in all of the calculations presented below, where Rg is taken as the block copolymer radius of gyration, and we vary the length of the grafted chains Ng, the grafting density σ, and the volume fraction ϕNP of the grafted nanoparticles.
Results
Homopolymer in an implicit solvent
We begin with a brief comparison of the DMFT method to other simulation approaches; to that end, we use the Gaussian-regularized Edwards model44 to make a straightforward comparison to both particle-based methods (dissipative particle dynamics, DPD) and to complex Langevin (CL) field-theoretic simulations. In all cases, we discretize our chains into N = 20 interaction sites per chain. First, we examine the extent to which the DMFT method captures thermodynamic fluctuation effects by comparing the osmotic pressure calculated using each technique as a function of the polymer concentration C = ρ0Rg3/N, where ρ0 is the monomer density. As C → ∞, the osmotic pressure should approach the mean-field value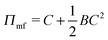 , where
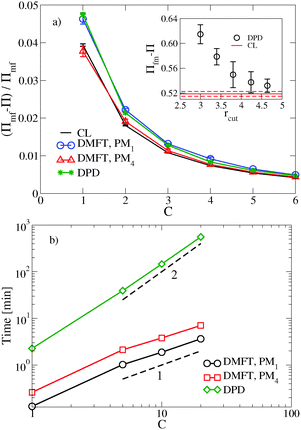
, where 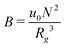 is the dimensionless interaction strength that measures the quality of the implicit solvent. Fluctuation effects become increasingly important as C is decreased. Fig. 2a compares Π calculated from the three techniques, and the results for the DMFT are shown for two interpolation schemes, a first-order scheme (PM1) and a fourth-order scheme (PM4). We take the CL results as the exact result since the method does not require the use of a potential cut-off as the DPD method does, and we note that we did not perform long-range corrections to the pressure and energy in the DPD implementation of the model. When we use the PM1 interpolation scheme, the relative fluctuation effects are slightly exaggerated in the DMFT results compared to the CL results, and they are comparable to the DPD results with a potential cut-off of rcut = 3b, where b is the standard deviation of the Gaussian interaction potential. The inset to Fig. 2a demonstrates that increasing the cut-off in the DPD method causes the results to approach the CL result. When the interpolation scheme used in DMFT is the higher order PM4 scheme, the results are numerically indistinguishable from the CL results, suggesting that the DMFT method accurately captures the fluctuation effects.
is the dimensionless interaction strength that measures the quality of the implicit solvent. Fluctuation effects become increasingly important as C is decreased. Fig. 2a compares Π calculated from the three techniques, and the results for the DMFT are shown for two interpolation schemes, a first-order scheme (PM1) and a fourth-order scheme (PM4). We take the CL results as the exact result since the method does not require the use of a potential cut-off as the DPD method does, and we note that we did not perform long-range corrections to the pressure and energy in the DPD implementation of the model. When we use the PM1 interpolation scheme, the relative fluctuation effects are slightly exaggerated in the DMFT results compared to the CL results, and they are comparable to the DPD results with a potential cut-off of rcut = 3b, where b is the standard deviation of the Gaussian interaction potential. The inset to Fig. 2a demonstrates that increasing the cut-off in the DPD method causes the results to approach the CL result. When the interpolation scheme used in DMFT is the higher order PM4 scheme, the results are numerically indistinguishable from the CL results, suggesting that the DMFT method accurately captures the fluctuation effects.
Fig. 2b shows how the computational expense per time step of DMFT compares with DPD as a function of the polymer concentration. Recall that as C = ρ0Rg3/N increases at fixed chain discretization N, the monomer density ρ0 increases. At all C values, the DMFT method is faster than DPD, and importantly the DMFT method scales more effectively with the polymer concentration C. At C = 1, which corresponds approximately to a polystyrene (PS) with molecular weight Mw ≈ 7.5 kg mol−1, the DMFT method is 5–10 times faster than DPD, and at C = 5, which corresponds approximately to PS at Mw ≈ 175 kg mol−1, the DMFT method is 50–100 times faster. In going from the PM1 scheme to the PM4 scheme, the DMFT method loses approximately a factor of two in its speed per time step. The scaling with C in both methods can be easily understood: as C increases, the number of monomers in a fixed simulation volume will increase linearly with C, adding a factor of ![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) (nN) to the expense of both methods, where nN is the total number of segments in the simulation box. In DPD, the forces are calculated by summing over the neighbors of each particle, and the number of neighbors also increases with increased density, leading to a total
(nN) to the expense of both methods, where nN is the total number of segments in the simulation box. In DPD, the forces are calculated by summing over the neighbors of each particle, and the number of neighbors also increases with increased density, leading to a total ![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) [(nN)2] for DPD. In contrast, the DMFT method only has to sum over a fixed number of neighboring grid points when mapping the densities and forces between the particle and mesh scales, which are constant as a function of C.
[(nN)2] for DPD. In contrast, the DMFT method only has to sum over a fixed number of neighboring grid points when mapping the densities and forces between the particle and mesh scales, which are constant as a function of C.
DMFT can also be used to efficiently calculate equilibrium properties. The estimate of Π converges more rapidly using DMFT compared to the CL simulations at all C values tested. At C = 1, which corresponds to a strongly fluctuating field theory, DMFT using the PM1 interpolation scheme requires approximately 50 times less CPU time to obtain an estimate of Π that is within 5% of the final value. At C = 6, where the field fluctuations are reduced, the DMFT method is only approximately 20 times faster. Using the more accurate PM4 route would reduce the relative speedup of DMFT over CL by a factor of approximately 2.5. While further tests would be needed to elucidate the relative efficiency of the two methods in more complicated systems such as block copolymers, our results demonstrate that the DMFT approach is very competitive with the complex Langevin technique for sampling the equilibrium properties of a fully fluctuating field theory, particularly at low C values that are most relevant to experiments.
Solvent annealing in block copolymer nanocomposite thin films
Having established that the DMFT method provides an efficient and reasonable description of the thermodynamics for a model polymer system, we next turn our attention to the effect of solvent annealing on the distribution of grafted nanoparticles in block copolymer thin films. We employ the model described above with a lamellar-forming block copolymer with fA = NA/N = 0.5, N = 60, κN = 250, and χABN = 70. Our polymer concentration is C = ρ0Rg3/N = 6, which corresponds to an invariant degree of polymerization![[N with combining macron]](https://www.rsc.org/images/entities/i_char_004e_0304.gif) = C263 ≈ 7.8 × 103 and approximately corresponds to a poly(styrene)-b-poly(methyl methacrylate) block copolymer with a molecular weight Mn = 250 kg mol−1. Unless otherwise specified, the nanoparticle volume fraction (core plus grafts) is held constant at ϕNP = 0.06 relative to the block copolymer in the dry film; the total number of nanoparticles varies from twelve to more than forty depending on the graft density and the graft length.
= C263 ≈ 7.8 × 103 and approximately corresponds to a poly(styrene)-b-poly(methyl methacrylate) block copolymer with a molecular weight Mn = 250 kg mol−1. Unless otherwise specified, the nanoparticle volume fraction (core plus grafts) is held constant at ϕNP = 0.06 relative to the block copolymer in the dry film; the total number of nanoparticles varies from twelve to more than forty depending on the graft density and the graft length.
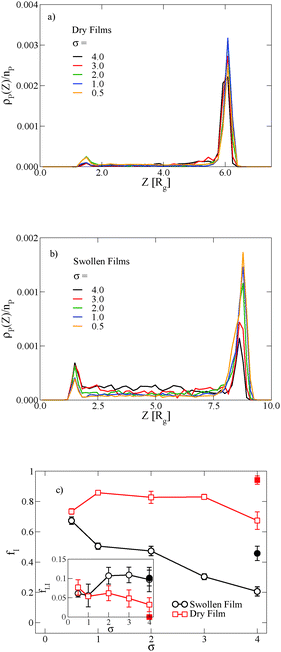
In thin films swollen with solvent at equilibrium, the distribution of grafted nanoparticles through the film thickness depends on the grafting density, while in dry films the nanoparticles are segregated to the soft interface. Fig. 3a and b show the distribution of particles as a function of z for the dry and swollen films, respectively. In the dry films, the nanoparticles predominantly reside at the soft interface near z ≈ 6Rg, although there is a slight enrichment of the particles near the hard substrate at z ≈ 1.5Rg, and these observations are largely independent of the grafting density. However, in the swollen films the distribution changes with grafting density; at higher grafting densities, the nanoparticles are more evenly distributed throughout the film. These differences are quantified by calculating the fraction of nanoparticles that are within 1.25 particle diameters of the top surface, fI, which is plotted in Fig. 3c. The fraction at the interface is approximately constant as a function of grafting density in the dry film, while fI decreases with increasing grafting density in the swollen film. We find that the neutral solvent is enriched at the soft interface between the block copolymer and the homopolymer phase, which displaces the nanoparticles. The inset to Fig. 3c shows that the fraction of particles at the lower surface is only weakly sensitive to the presence of solvent. The effects of solvent on the distribution of nanoparticles are expected to be sensitive to the relative surface activity of the solvent compared to the particles, which will depend on the various interactions between the chemical species.
The distribution of nanoparticles depends on the overall nanoparticle concentration. At the concentrations used to generate the data in Fig. 3a and b, the top surface becomes saturated with grafted nanoparticles in the dry film, which precludes more particles from segregating to the surface. We verify this result by reducing the nanoparticle volume fraction to ϕNP = 0.03 for σ = 4, and the results are shown as solid symbols in Fig. 3c. The overall fraction at the interface increases as the nanoparticle concentration is reduced, but the contrast in the swollen and dry states remains: a smaller fraction of the nanoparticles remains at the interface in the swollen state compared to the dry state.
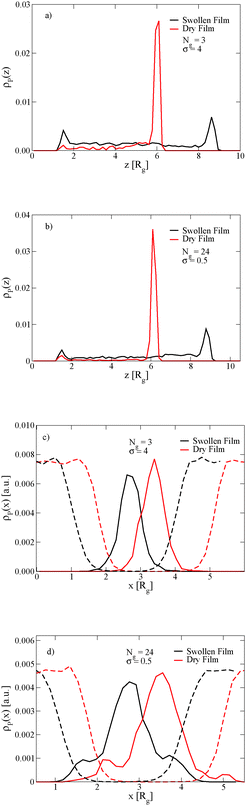
The length of the grafted chains also affects the distribution of the nanoparticles throughout the block copolymer film. Since we expect the relative total volume of the grafted chains to the nanoparticle core to affect the distribution of the particles, to isolate the effect of N we simultaneously vary σ to keep the total volume of grafted chains per nanoparticle constant. Fig. 4a shows the distribution of nanoparticles through the film thickness in the swollen and dry states for Ng = 3, σ = 4, while Fig. 4b shows the distribution with longer grafted chains Ng = 24, σ = 0.5. In both cases, when the film is swollen with solvent the nanoparticles are more evenly distributed throughout the film thickness. We note that when the short chains are grafted on the nanoparticle surface at the lower grafting density of σ = 0.5, the nanoparticles were strongly bound to the interface in both the swollen and the dry state (see Fig. 3c), while the longer chains aid in the nanoparticle dispersion throughout the film thickness even at a lower grafting density.
The position of the nanoparticles in the direction normal to the A–B lamellar interface is also controlled by the length of the grafted chains. Fig. 4c and d show that the nanoparticles with short grafted chains at the higher graft density are more strongly bound to the center of the lamellar domain, while the grafted particles with longer chains and the lower grafting density have a small peak in their density off of the center of the lamellar domain. In both cases, these observations are independent of the film being swollen with solvent.
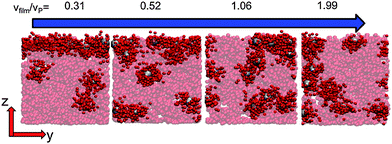
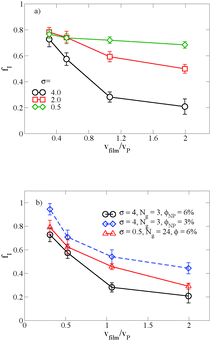
When there is a difference in the equilibrium distribution of grafted nanoparticles in the dry and swollen states, we can tune the final distribution of nanoparticles in the dry films by varying the solvent evaporation rate. Fig. 5 shows the images of the final grafted nanoparticle distribution with Ng = 3, σ = 4 in a dry block copolymer with increasing solvent evaporation rate. At low evaporation rates, the nanoparticles have sufficient time to diffuse to their equilibrium distribution in the dry film near the soft interface. In contrast, at higher evaporation rates the nanoparticles experience an affine transformation in their z-position as the block copolymer composite film contracts, remaining trapped in their distribution in the swollen state. We quantify this observation by plotting the final fraction of nanoparticles at the interface after drying the film, fI, as a function of the film contraction rate 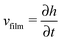 normalized by the nanoparticle diffusion rate, vP = DNP/RP; the diffusion coefficient of the nanoparticle DNP is taken as the value of a nanoparticle with a given σ and Ng in a homopolymer melt with N = 60. Fig. 6a shows the fraction of particles that remain at the soft interface fI between the block copolymer and the homopolymer overlayer as a function of vfilm/vP. At low grafting densities when the nanoparticles remain at the interface in both the dry and swollen states, the final fraction of particles at the interface upon drying is invariant with the evaporation rate. In contrast, at higher grafting densities where there is a notable difference in the nanoparticle distribution in the dry and swollen states, the final nanoparticle distribution can be controlled by varying the solvent evaporation rate.
normalized by the nanoparticle diffusion rate, vP = DNP/RP; the diffusion coefficient of the nanoparticle DNP is taken as the value of a nanoparticle with a given σ and Ng in a homopolymer melt with N = 60. Fig. 6a shows the fraction of particles that remain at the soft interface fI between the block copolymer and the homopolymer overlayer as a function of vfilm/vP. At low grafting densities when the nanoparticles remain at the interface in both the dry and swollen states, the final fraction of particles at the interface upon drying is invariant with the evaporation rate. In contrast, at higher grafting densities where there is a notable difference in the nanoparticle distribution in the dry and swollen states, the final nanoparticle distribution can be controlled by varying the solvent evaporation rate.
Fig. 6b shows the effect of varying either the nanoparticle concentration or the grafted chain length on these results. When the particle concentration is reduced from ϕNP = 0.06 to 0.03, the same trend emerges, though fI is shifted to larger values; as described above, this is a result of crowding at the free surface of the A domain in the block copolymer, which becomes saturated at the higher grafted nanoparticle concentration. Similarly, when we increase the grafted chain length while simultaneously reducing the graft density to maintain the same overall nanoparticle volume, we demonstrate that we are able to tune the distribution of nanoparticles by controlling vfilm/vP. For a polymer matrix that undergoes its glass transition upon drying, these results could potentially provide a route towards trapping nanoparticles throughout the film thickness rather than at the free interface. Our results also highlight the importance of understanding the equilibrium distribution in the presence and the absence of solvent and how it affects the final distribution in the dry film.
Discussion
In this manuscript, we have implemented and extended the dynamic mean field theory proposed by Fredrickson and Orland to study the effects of solvent vapor annealing on the distribution of grafted nanoparticles in block copolymer thin films. The primary attractive feature of this approach is that it is based on the MSR path integral description of the system's dynamics rather than postulating the equations of motion. While not performed here, in the future this formally exact representation of the system's dynamics could potentially enable either an analytic understanding of the approximations involved or extending the framework to relax the approximations by going beyond the dynamic mean-field approximation. In this work, we were able to follow the approach of Fredrickson and Orland to justify the simplified dynamic mean field theory when using a significantly more efficient equation of motion. This framework could also be useful for the study of semiflexible polymer systems and other polymeric materials with anisotropic interactions (e.g. liquid crystalline polymers), which are computationally demanding to study using conventional field theoretic simulations.One primary assumption in our method is that our current implementation does not capture entanglement effects on the dynamics. This could be easily implemented through the use of slip-links, as has been done by several authors recently,74–76 or through an interesting alternative suggestion by Grzetic et al.54 where the forces are projected along the polymer backbone, suppressing transverse motion of the polymer chains. Another assumption of the current implementation is our neglect of hydrodynamic interactions; however, the MSR framework may be exploited to relax this assumption in the future. For example, prior analytic studies using the MSR path integral approach to study polymer solutions in an implicit solvent have included hydrodynamic interactions between the polymer monomers,62 the effects of which are neglected in the current work. Another strategy for capturing hydrodynamic effects could be to cast the equations of motion in a manner that locally conserves momentum similar to the DPD equations.77
Other than the computational efficiency of the approach, another significant advantage of the approach is that it apparently samples the equilibrium properties of the fluctuating field theory despite the dynamic mean field approximation used in the derivation of the theory. This is particularly important because the DMFT framework does not suffer from the limitations of typical implementations of complex Langevin simulations that require using non-bonded potential energy functions that possess a functional inverse.27 The use of more general non-bonded functions could be exploited to use functions systematically derived from liquid state theory that are expected to more quantitatively reproduce the thermodynamics of polymer melts.78–80 With the recent development of a scheme for including charges in the related SCMF approach,81,82 we also anticipate that we will be able to predict the dynamics and thermodynamics of systems containing charged nanoparticles and/or charged polymers.
Our solvent annealing results demonstrate a means to tune the distribution of nanoparticles in a block copolymer thin film using solvent vapor annealing. At equilibrium for the set of interaction parameters considered here, the nanoparticles tended to segregate to the soft interface between a homopolymer layer and the block copolymer film in the absence of solvent. Upon addition of solvent, depending on the grafted chain length and grafting density, the nanoparticles were displaced by the solvent into the bulk of the film. We then demonstrated that this change in the nanoparticle distribution could be exploited to tune the final distribution of the nanoparticles through the film thickness by varying the solvent evaporation rate relative to the nanoparticle diffusion time. One could use such a strategy to trap particles in a metastable distribution through the film.
Acknowledgements
We are grateful for funding provided by the Petroleum Research Fund managed by the American Chemical Society ACS PRF 55662-ND7 (H. C., R. A. R.), and the Nation Science Foundation through grants NSF DMR-141024 (J. K.) and NSF CBET-1510635 (partial support for RAR). Computational resources were provided by the National Institute for Computational Sciences at the University of Tennessee through an XSEDE allocation, TG-DMR150034.References
- C. M. Bates, M. J. Maher, D. W. Janes, C. J. Ellison and C. G. Willson, Macromolecules, 2014, 47, 2 CrossRef CAS.
- R. Ruiz, H. Kang, F. A. Detcheverry, E. Dobisz, D. S. Kercher, T. R. Albrecht, J. J. de Pablo and P. F. Nealey, Science, 2008, 321, 936 CrossRef CAS PubMed.
- G. H. Fredrickson and F. S. Bates, Annu. Rev. Mater. Sci., 1996, 26, 501 CrossRef CAS.
- M. A. Hillmyer, Adv. Polym. Sci., 2005, 190, 137 CrossRef CAS.
- I. W. Hamley, Nanotechnology, 2003, 14, R39 CrossRef CAS.
- S. Kim, M. Misner, T. Xu, M. Kimura and T. Russell, Adv. Mater., 2004, 16, 226 CrossRef CAS.
- W. A. Phillip, B. O'Neill, M. Rodwogin, M. A. Hillmyer and E. L. Cussler, ACS Appl. Mater. Interfaces, 2010, 2, 847 CAS.
- C. Sinturel, M. Vayer, M. Morris and M. a. Hillmyer, Macromolecules, 2013, 46, 5399 CrossRef CAS.
- S. P. Paradiso, K. T. Delaney, C. J. Garca-Cervera, H. D. Ceniceros and G. H. Fredrickson, ACS Macro Lett., 2014, 3, 16 CrossRef CAS.
- S.-M. Hur, G. S. Khaira, A. Ramrez-Hernández, M. Müller, P. F. Nealey and J. J. de Pablo, ACS Macro Lett., 2015, 4, 11 CrossRef CAS.
- S. P. Paradiso, K. T. Delaney, C. J. Garca-Cervera, H. D. Ceniceros and G. H. Fredrickson, Macromolecules, 2016, 49, 1743 CrossRef CAS.
- H. Chao and R. A. Riggleman, Polymer, 2013, 54, 5222 CrossRef CAS.
- J. F. Moll, P. Akcora, A. Rungta, S. Gong, R. H. Colby, B. C. Benicewicz and S. K. Kumar, Macromolecules, 2011, 44, 7473 CrossRef CAS.
- R. A. Riggleman, G. Toepperwein, G. J. Papakonstantopoulos, J.-L. Barrat and J. J. de Pablo, J. Chem. Phys., 2009, 130, 244903 CrossRef PubMed.
- G. N. Toepperwein, N. C. Karayiannis, R. A. Riggleman, M. Kroger and J. J. de Pablo, Macromolecules, 2011, 44, 1034 CrossRef CAS.
- M. R. Bockstaller, R. A. Mickiewicz and E. L. Thomas, Adv. Mater., 2005, 17, 1331 CrossRef CAS.
- S. K. Kumar, N. Jouault, B. Benicewicz and T. Neely, Macromolecules, 2013, 46, 3199 CrossRef CAS.
- M. J. A. Hore and R. J. Composto, ACS Nano, 2010, 4, 6941 CrossRef CAS PubMed.
- M. Moniruzzaman and K. I. Winey, Macromolecules, 2006, 39, 5194 CrossRef CAS.
- P. F. Green, Soft Matter, 2011, 7, 7914 RSC.
- S. Srivastava, J. L. Schaefer, Z. Yang, Z. Tu and L. A. Archer, Adv. Mater., 2013, 26, 1 CrossRef.
- H. Chao, B. A. Hagberg and R. A. Riggleman, Soft Matter, 2014, 10, 8083 RSC.
- P. Akcora, H. Liu, S. K. Kumar, J. Moll, Y. Li, B. C. Benicewicz, L. S. Schadler, D. Acehan, A. Z. Panagiotopoulos, V. Pryamitsyn, V. Ganesan, J. Ilavsky, P. Thiyagarajan, R. H. Colby and J. F. Douglas, Nat. Mater., 2009, 8, 354 CrossRef CAS PubMed.
- H.-J. Chung, J. Kim, K. Ohno and R. J. Composto, ACS Macro Lett., 2012, 1, 252 CrossRef CAS.
- M. Mu, N. Clarke, R. J. Composto and K. I. Winey, Macromolecules, 2009, 42, 7091 CrossRef CAS.
- J. Choi, N. Clarke, K. I. Winey and R. J. Composto, ACS Macro Lett., 2014, 3, 886 CrossRef CAS.
- G. H. Fredrickson, The Equilibrium Theory of Inhomogeneous Polymers, Oxford University Press, New York, 2006 Search PubMed.
- M. Matsen, J. Phys.: Condens. Matter, 2001, 14, 21 CrossRef.
- R. A. Riggleman, R. Kumar and G. H. Fredrickson, J. Chem. Phys., 2012, 136, 024903 CrossRef PubMed.
- Q. Wang, T. Taniguchi and G. H. Fredrickson, J. Phys. Chem. B, 2004, 108, 6733 CrossRef CAS.
- X. Man, K. T. Delaney, M. C. Villet, H. Orland and G. H. Fredrickson, J. Chem. Phys., 2014, 140, 024905 CrossRef PubMed.
- P. M. Chaikin and T. C. Lubensky, Principles of condensed matter physics, Cambridge Univ. Press, 2000, vol. 1 Search PubMed.
- V. Ganesan and G. H. Fredrickson, Europhys. Lett., 2001, 55, 814 CrossRef CAS.
- G. H. Fredrickson, V. Ganesan and F. Drolet, Macromolecules, 2002, 35, 16 CrossRef CAS.
- S. Sides, B. Kim, E. Kramer and G. Fredrickson, Phys. Rev. Lett., 2006, 96, 250601 CrossRef PubMed.
- S. H. Kim and E. W. Cochran, Polymer, 2011, 52, 2328 CrossRef CAS.
- R. C. Ferrier Jr, J. Koski, R. A. Riggleman and R. J. Composto, Macromolecules, 2016, 49, 1002 CrossRef.
- R. B. Thompson, V. V. Ginzburg, M. W. Matsen and A. C. Balazs, Macromolecules, 2002, 35, 1060 CrossRef CAS.
- R. B. Thompson, V. V. Ginzburg, M. W. Matsen and A. C. Balazs, Science, 2001, 292, 2469 CrossRef CAS PubMed.
- K. Hur, R. G. Hennig, F. A. Escobedo and U. Wiesner, J. Chem. Phys., 2010, 133, 194108 CrossRef PubMed.
- S.-m. Hur, C. J. Garc and G. H. Fredrickson, Macromolecules, 2012, 45, 2905 CrossRef CAS.
- J. Koski, H. Chao and R. A. Riggleman, J. Chem. Phys., 2013, 139, 244911 CrossRef PubMed.
- J. Koski, H. Chao and R. A. Riggleman, Chem. Commun., 2015, 51, 5440 RSC.
- M. C. Villet and G. H. Fredrickson, J. Chem. Phys., 2014, 141, 224115 CrossRef PubMed.
- J. Koski, B. Hagberg and R. A. Riggleman, Macromol. Chem. Phys., 2016, 217, 509 CrossRef CAS.
- J. G. E. M. Fraaije, J. Chem. Phys., 1993, 99, 9202 CrossRef CAS.
- M. Doi and A. Onuki, J. Phys. II, 1992, 2, 1631 CrossRef CAS.
- S. T. Milner, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1993, 48, 3674 CrossRef CAS.
- G. Fredrickson, V. Ganesan and F. Drolet, Macromolecules, 2002, 35, 16 CrossRef CAS.
- H. D. Ceniceros, G. H. Fredrickson and G. O. Mohler, J. Comput. Phys., 2009, 228, 1624 CrossRef CAS.
- D. M. Hall, T. Lookman, G. H. Fredrickson and S. Banerjee, J. Comput. Phys., 2007, 224, 681 CrossRef CAS.
- D. M. Hall, T. Lookman, G. H. Fredrickson and S. Banerjee, Phys. Rev. Lett., 2006, 97, 114501 CrossRef PubMed.
- G. H. Fredrickson and H. Orland, J. Chem. Phys., 2014, 140, 084902 CrossRef PubMed.
- D. J. Grzetic, R. A. Wickham and A.-C. Shi, J. Chem. Phys., 2014, 140, 244907 CrossRef PubMed.
- P. C. Martin, E. D. Siggia and H. A. Rose, Phys. Rev. A: At., Mol., Opt. Phys., 1973, 8, 423 CrossRef.
- R. V. Jensen, J. Stat. Phys., 1981, 25, 183 CrossRef.
- C. De Dominicis, J. Phys., Colloq., 1976, 37, C1 CrossRef.
- B. Narayanan, V. a. Pryamitsyn and V. Ganesan, Macromolecules, 2004, 37, 10180 CrossRef CAS.
- N. A. Kumar and V. Ganesan, J. Chem. Phys., 2012, 101101, 10 Search PubMed.
- K. C. Daoulas, M. Müller, M. P. Stoykovich, S.-M. Park, Y. J. Papakonstantopoulos, J. J. de Pablo, P. F. Nealey and H. H. Solak, Phys. Rev. Lett., 2006, 96, 036104 CrossRef PubMed.
- M. Müller and F. Schmid, Adv. Polym. Sci., 2005, 185, 1 CrossRef.
- G. H. Fredrickson and E. Helfand, J. Chem. Phys., 1990, 93, 2048 CrossRef CAS.
- R. W. Hockney and J. W. Eastwood, Computer Simulation Using Particles, Taylor & Francis, Inc., Bristol, PA, USA, 1988 Search PubMed.
- M. Deserno and C. Holm, J. Chem. Phys., 1998, 109, 7678 CrossRef CAS.
- D. Frenkel and B. Smit, Understanding Molecular Simulations: From Algorithms to Applications, Academic Press, San Diego, 2002 Search PubMed.
- A.-C. Shi and J. Noolandi, Macromol. Theory Simul., 1999, 8, 214 CrossRef CAS.
- M. Frigo and S. Johnson, in Proceedings of the 1998 IEEE International Conference on Acoustics, Speech and Signal Processing, ICASSP '98IEEE, 1998, vol. 3, pp. 1381–1384.
- N. Grønbech-Jensen and O. Farago, Mol. Phys., 2013, 111, 983 CrossRef.
- E. Helfand, J. Chem. Phys., 1975, 62, 999 CrossRef CAS.
- I. M. Ilie, W. J. Briels and W. K. den Otter, J. Chem. Phys., 2015, 142, 114103 CrossRef PubMed.
- M. W. Matsen, J. Chem. Phys., 1997, 106, 7781 CrossRef CAS.
- P. Stasiak, J. D. McGraw, K. Dalnoki-Veress and M. W. Matsen, Macromolecules, 2012, 45, 9531 CrossRef CAS.
- S.-M. Hur, M. S. Onses, A. Ramrez-Hernández, P. F. Nealey, J. A. Rogers and J. J. de Pablo, Macromolecules, 2015, 48, 4717 CrossRef CAS.
- A. Nikoubashman, R. L. Davis, B. T. Michal, P. M. Chaikin, R. A. Register and A. Z. Panagiotopoulos, ACS Nano, 2014, 8, 8015 CrossRef CAS PubMed.
- A. Ramrez-hernández, B. L. Peters, M. Andreev, J. D. Schieber and J. J. D. Pablo, J. Chem. Phys., 2015, 143, 243147 CrossRef PubMed.
- A. E. Likhtman, Macromolecules, 2005, 38, 6128 CrossRef CAS.
- P. Español, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1995, 52, 1734 CrossRef.
- A. J. Clark, J. McCarty, I. Y. Lyubimov and M. G. Guenza, Phys. Rev. Lett., 2012, 109, 168301 CrossRef CAS PubMed.
- D. Yang and Q. Wang, Soft Matter, 2015, 11, 7109 RSC.
- D. Yang and Q. Wang, J. Chem. Phys., 2015, 142, 7109 Search PubMed.
- G. Pandav, V. Pryamitsyn and V. Ganesan, Langmuir, 2015, 31, 12328 CrossRef CAS PubMed.
- G. Pandav, V. Pryamitsyn, J. Errington and V. Ganesan, J. Phys. Chem. B, 2015, 119, 14536 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c6sm00770h |
| This journal is © The Royal Society of Chemistry 2017 |