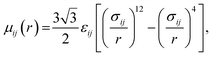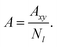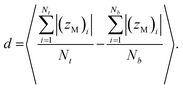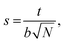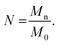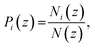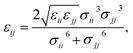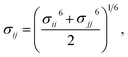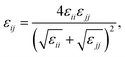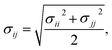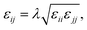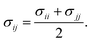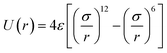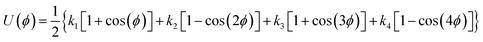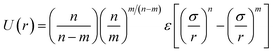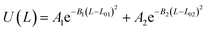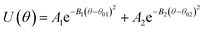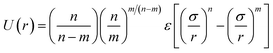DOI:
10.1039/C7RA10573H
(Paper)
RSC Adv., 2017,
7, 54756-54771
Chemically specific coarse-grained models to investigate the structure of biomimetic membranes†
Received
24th September 2017
, Accepted 13th November 2017
First published on 29th November 2017
Abstract
Biomimetic polymer/protein membranes are promising materials for DNA sequencing, sensors, drug delivery and water purification. These self-assembled structures are made from low molecular weight amphiphilic block copolymers (Nhydrophobic < 40 for a diblock copolymer), including poly(ethylene oxide)–1,2-polybutadiene (EO–1,2-BD) and poly(ethylene oxide)–poly(ethyl ethylene) (EO–EE). To examine these membranes' nanoscale structure, we developed a coarse-grained molecular dynamics (CG MD) model for EO–1,2-BD and assembled a CG MD model for EO–EE using parameters from two published force fields. We observe that the polymers' hydrophobic core blocks are slightly stretched compared to the random coil configuration seen at higher molecular weights. We also observe an increase in the interdigitation of the hydrophobic leaflets with increasing molecular weight (consistent with literature). The hydration level of the EO corona (which may influence protein incorporation) is higher for membranes with a larger area/chain, regardless of whether EE or 1,2-BD forms the hydrophobic block. Our results provide a molecular-scale view of membrane packing and hydrophobicity, two important properties for creating polymer–protein biomimetic membranes.
1. Introduction
Biomimetic membranes containing transmembrane proteins are being extensively studied for use in drug and gene delivery, sensors, reactive surfaces and water purification.1–11 There have even been some recent commercialization successes – products in this area currently include the popular low cost DNA sequencer (MinION) from Oxford Nanopore Technologies12 and the Aquaporin Inside™ forward osmosis water purification membranes manufactured by Aquaporin A/S.13 Block copolymers (BCs) are proposed as alternatives to lipids because they offer improved chemical14 and mechanical15,16 stability and the ability to incorporate transmembrane proteins.11 This improvement in physical and chemical stability is attractive from an applications perspective: for example, BC membranes incorporating transmembrane water transport proteins or artificial water channels have been widely examined as selectively permeable membranes for separations such as reverse osmosis (reviewed by Kumar et al.11).
The morphology of self-assembled block copolymers depends on the volume fraction of each block (described by the hydrophilic volume fraction, f); the chain length (degree of polymerization N); and the effective interaction parameter (χ) between the two blocks, which depends on the difference in their hydrophobicities. Thus, copolymer membrane properties can be tuned by changing the block molecular weights (f, N) and polymer identity (χ).17 Polymer molecular weights and identity are easily manipulated in simulations once a force field is developed, making simulations an important tool for investigating the properties of biomimetic membranes. In addition, simulations allow researchers to visualize polymer membranes at the molecular scale, and can aid in understanding the connection between monomer interactions and membrane properties.
In this work we present coarse-grained molecular dynamics (CG MD) models for two biomimetic-membrane-relevant block copolymers: poly(ethylene oxide)–poly(1,2-butadiene) (EO–1,2-BD) and poly(ethylene oxide)–poly(ethyl ethylene) (EO–EE). Coarse-grained molecular dynamics simulations can extend all atom (AA) simulations to longer time and length scales due to the reduced number of force sites (each CG bead corresponds to multiple atoms). Reduced numbers of CG force sites enable shorter computational times for studying self-assembly of polymers compared to atomistic approaches. We focused on low molecular weight polymers (12–40 hydrophobic monomers per chain) as these are appropriate for biomimetic membrane applications due to the need to approximately match the thickness of the block copolymer's hydrophobic domain with that of the membrane-spanning region of membrane proteins. 1,2-BD and EE, have similar structures, but 1,2-BD is less hydrophobic, having a Hildebrand solubility parameter δ = 16.7 MPa1/2 compared to δ = 14.2 MPa1/2 for EE (obtained using Fedors' group contribution method18,19). Using these CG models, we examine the changes in membrane structure and hydration due to this hydrophobicity difference between 1,2-BD and EE, as well as the membrane thickness and area per chain of the low-molecular-weight membranes used for protein incorporation. We use the bottom-up coarse-graining approach, in which polymer-specific differences are captured by parameterizing the CG forces to reproduce properties from the corresponding atomistic simulations20,21 and experimental data. In the models we present, we use one type of coarse-grained bead to represent each type of monomer and one type of bead to represent three water molecules. A schematic representation of the proposed level of coarse-graining is presented in Fig. 1.
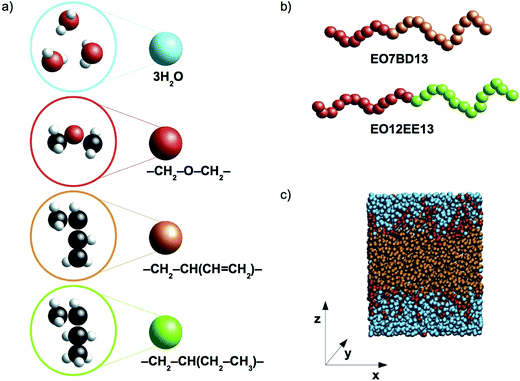 |
| | Fig. 1 Schematic representations and a simulation snapshot. (a) The level of coarse-graining used to represent water and polymers. From top to bottom, water, poly(ethylene oxide) (EO), 1,2-polybutadiene (1,2-BD) and poly(ethyl ethylene) (EE) are shown in atomistic detail and as coarse-grained beads. Examples of the CG block copolymers are given in (b), and in (c) a simulation snapshot is presented. Our simulations use a Cartesian coordinate system in which the z-axis is normal to the plane of the membrane. | |
Our methods and results are organized as follows. First, we present the development of our CG force field for EO–1,2-BD, which is optimized to reproduce data from atomistic simulations and cryogenic transmission electron microscopy (cryo-TEM) experiments. We assemble the EO–EE model based on previously published parameters by Klein and coworkers22–25 and cryo-TEM data. To ensure compatibility between the EO, EE, and 1,2-BD parameters, we parameterize the new bonded parameters in our models using Iterative Boltzmann Inversion (IBI) with structures from OPLS-all-atom simulations as a target, as was done by Klein et al. for the EO–EE22,23 and EO–ethylene (EO–PE)24,25 models from which we draw parameters. We then show that this simplified model for EO–EE (which lacks unique end or junction beads) can reproduce membrane thickness and area per chain data from previous experiments16,26 and simulations.23
For the various nonbonded interactions in EO–EE and EO–PE, Klein and coworkers used a variety of structural and thermodynamic properties as targets, such as density,22–25 surface tension,22–25 interface width,24 hydration free energy,24,25 and the spacing and area/molecule of EO-containing surfactant lamellae.24,25 We tuned the nonbonded cross-interactions between the CG beads to match membrane thickness data from cryo-TEM experiments. 1,2-BD self-interactions are tuned to match density and atomistic radial distribution functions (RDFs), as is commonly done when atomistic trajectories are available.27–31 We test a variety of combining rules, and find that a modified Lorentz–Berthelot (LB) relationship can reproduce the experimental data.
Using these CG models for EO–EE and EO–1,2-BD, we determine the scaling relationships between membrane structural properties (thickness and area per chain) and molecular weight for low-molecular-weight membranes. Finally, based on the calculated density profiles, we examined the increase in the interdigitation of the hydrophobic leaflets as their molecular weight increases, as well as the possibility that the EO corona might be less hydrated for a membrane with a more hydrophobic core block.
2. Models and methods
2.1 Coarse-grain model development
1,2-BD. The CG 1,2-polybutadiene self-interactions were parameterized to reproduce the atomistic structure of the polymer melt. 1,2-BD atomistic simulations were performed using OPLS all-atom parameters32,33 and some additional parameters proposed by Okada et al.34 All atomistic parameters for 1,2-BD are presented in Table 1. Because the polybutadiene synthesized in our lab is an atactic polymer containing a 10% 1,4-butadiene impurity, we ran a number of short simulations to determine whether we could neglect this synthetic impurity and average over a number of atactic chains to account for the distribution of stereoisomers. These simulations are shown in ESI,† and indicate that we can make these simplifications, indicating that we can use a minimalistic model with only one bead type (1,2-BD) rather than having separate bead types for right-handed and left-handed stereoisomers or for 1,2 and 1,4-BD monomers. Thus, we used one CG bead to represent the center of mass for the 1,2-BD monomer and refined our CG bonded parameters using IBI,20,27 as was done by Klein and coworkers.22–25 For the non-bonded potential we used a Lennard-Jones-type function with exponent 9 for the repulsive and 6 for the attractive part of the potential (LJ9−6), that minimized the least-squared difference between the atomistic and CG radial distribution functions while maintaining a 1,2-BD melt density within 5% of the experimental value (0.9 g cm−3).34 The bond and angle potentials are given by a double-Gaussian function that minimized the least-squares difference between the distributions obtained from atomistic and CG simulations of the 1,2-BD melt. All CG parameters for the 1,2-BD polymer are provided in Table 2.
Table 1 Atomistic parameters for 1,2-polybutadiene (1,2-BD) melt and poly(ethylene oxide)–1,2-polybutadiene (EO–1,2-BD) block copolymer. The presented atomistic parameters are based on OPLS all-atom parameters32,33 and some additional parameters proposed by Okada et al.34
| Non-bonded atom |
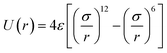
|
| ε (kcal mol−1) |
σ (Å) |
| HCT |
0.03 |
2.5 |
| HCM |
0.03 |
2.42 |
| CT |
0.066 |
3.5 |
| CM |
0.076 |
3.55 |
| OS |
0.14 |
2.9 |
| OH |
0.17 |
3.12 |
| HO |
0 |
0 |
| HCT |
0.03 |
2.5 |
| Bond |
U(L) = k(L − L0)2 |
| k (kcal mol−1 Å2) |
L0 (Å) |
| CT–HCT |
340 |
1.09 |
| CT–CT |
268 |
1.529 |
| CT–CM |
317 |
1.51 |
| CM–HCM |
340 |
1.08 |
| CM–CM |
549 |
1.34 |
| CT–OS |
320 |
1.41 |
| CT–OH |
320 |
1.41 |
| HO–OH |
553 |
0.945 |
| Angle |
U(θ) = k(θ − θ0)2 |
| k (kcal mol−1 rad2) |
θ0 (degrees) |
| HCT–CT–HCT |
33 |
107.8 |
| CT–CT–HCT |
37.5 |
110.7 |
| CT–CT–CT |
58.35 |
112.7 |
| CT–CT–CM |
63 |
111.1 |
| HCT–CT–CM |
35 |
109.5 |
| CT–CM–HCM |
35 |
117 |
| CT–CM–CM |
70 |
124 |
| HCM–CM–CM |
35 |
120 |
| HCM–CM–HCM |
35 |
117 |
| CT–CT–OS |
50 |
109.5 |
| CT–CT–OH |
50 |
109.5 |
| HCT–CT–OS |
35 |
109.5 |
| HCT–CT–OH |
35 |
109.5 |
| CT–OS–CT |
60 |
109.5 |
| Dihedral |
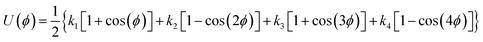
|
| k1 (kcal mol−1) |
k2 (kcal mol−1) |
k3 (kcal mol−1) |
k4 (kcal mol−1) |
| HCT–CT–CT–HCT |
0 |
0 |
0.3 |
0 |
| HCT–CT–CT–CT |
0 |
0 |
0.3 |
0 |
| HCT–CT–CT–CM |
0 |
0 |
0.366 |
0 |
| CT–CT–CT–CT |
1.3 |
−0.05 |
0.2 |
0 |
| HCT–CT–CM–HCM |
0 |
0 |
0.318 |
0 |
| HCT–CT–CM–CM |
0 |
0 |
−0.372 |
0 |
| CT–CT–CT–CM |
0 |
0 |
0 |
0 |
| HCM–CM–CM–HCM |
0 |
14 |
0 |
0 |
| HCM–CM–CT–CT |
−0.164418 |
−0.16265 |
0.567583 |
−0.161268 |
| CT–CT–CM–CM |
0.346 |
0.405 |
−0.904 |
0 |
| CT–CM–CM–HCM |
0 |
14 |
0 |
0 |
| CT–CM–CM–CT |
0 |
14 |
0 |
0 |
| CM–CT–CT–CM |
2.1 |
−1.022 |
−1.104 |
0 |
| HCT–CT–OS–CT |
0 |
0 |
0.76 |
0 |
| CT–OS–CT–CT |
0.65 |
−0.25 |
0.67 |
0 |
| OS–CT–CT–HCT |
0 |
0 |
0.468 |
0 |
| OH–CT–CT–HCT |
0 |
0 |
0.468 |
0 |
| OS–CT–CT–OS |
−0.55 |
0 |
0 |
0 |
| OH–CT–CT–OS |
4.319 |
0 |
0 |
0 |
| CT–CT–CT–OS |
1.711 |
−0.5 |
0.663 |
0 |
| HO–OH–CT–HCT |
0 |
0 |
0.3524 |
0 |
| HO–OH–CT–CT |
−0.356 |
−0.174 |
0.492 |
0 |
Table 2 Coarse grained parameters for 1,2-polybutadiene (1,2-BD) melt and poly(ethylene oxide)–1,2-polybutadiene (EO–1,2-BD) block copolymer
| Non-bonded bead |
LJm−n |
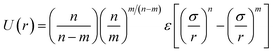
|
| ε (kcal mol−1) |
σ (Å) |
| The parameters given by Shinoda.22,23 All non-bonded cross interactions parameters are given by modified Lorentz–Berthelot combining rules with scaling factor λ = 0.3 (see eqn (12) and (13)). |
| EO |
LJ9−6 |
0.405a |
4.25a |
| BD |
LJ9−6 |
0.260 |
5.00 |
| W |
LJ12−4 |
0.895a |
4.37a |
| Bond |
U(L) = k(L − L0)2 |
| k (kcal mol−1 Å−2) |
L0 (Å) |
| EO–EO |
4.520a |
2.970a |
| |
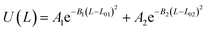
|
| A1 (kcal mol−1) |
B1 (Å−2) |
L01 (Å) |
A2 (kcal mol−1) |
B2 (Å−2) |
L02 (Å) |
| EO–BD |
0.236 |
48.5 |
2.86 |
0.812 |
29.0 |
3.27 |
| BD–BD |
0.148 |
33.3 |
3.06 |
0.127 |
5.21 |
3.55 |
| Angle |
U(θ) = k(θ − θ0)2 |
| k (kcal mol−1 rad2) |
θ0 (degrees) |
| EO–EO–EO |
1.987a |
138a |
| |
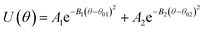
|
| A1 (kcal mol−1) |
B1 (deg−2) |
θ01 (degrees) |
A2 (kcal mol−1) |
B2 (deg−2) |
θ02 (degrees) |
| EO–EO–BD |
1.65 |
0.00113 |
140 |
1.92 |
0.00561 |
171 |
| EO–BD–BD |
0.996 |
0.00420 |
92.8 |
1.60 |
0.00425 |
128 |
| BD–BD–BD |
0.858 |
0.00285 |
100 |
1.30 |
0.00253 |
132 |
To perform atomistic simulations of the 1,2-BD homopolymer, we generated a melt containing 53 chains of 18 monomers each at density 1 g cm−3 using the amorphous cell builder in Accelrys Materials Studio (version 7.0).35 Because the 1,2-BD produced in our lab is atactic, we simulated a melt containing 53 unique atactic chains. The melt simulation was run until the radial, bond and angle distribution functions had converged (60 ns), and then this equilibrated structure was used as the initial configuration for a 95 ns simulation to obtain radial, bond, and angle distribution functions. A comparison of the atomistic targets and CG distribution functions obtained from the proposed CG model for the 1,2-BD melt is shown in Fig. 2.
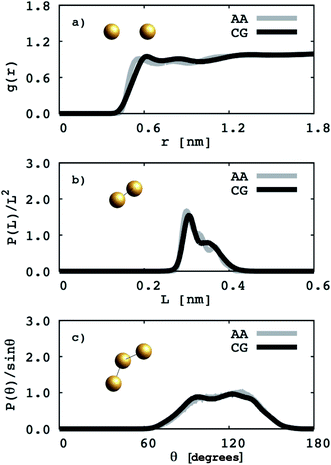 |
| | Fig. 2 Coarse grained (CG) and atomistic (AA) distributions for the 1,2-polybutadiene (1,2-BD) melt. Black lines indicate coarse grained distributions and gray lines represent the distributions derived from atomistic simulations. The radial distribution function for the 1,2-BD bead is given in (a). The distributions of bond lengths between 1,2-BD beads are presented in (b) and in (c) the bond angle distribution between 1,2-BD beads is presented. | |
EO–1,2-BD. The CG bonded parameters for the EO–1,2-BD junction were obtained based on atomistic simulations of a single block copolymer chain in vacuum, a method previously shown to reproduce polymer melt structure.36,37 As an addition test of our method's validity, we show in ESI† that the simplified CG EO–EE model we construct based on published parameters (in which bonded parameters are also obtained from OPLS-AA simulation results using Iterative Boltzmann Inversion) gives the same bonded structure in the membrane and in vacuum. Because of 1,2-BD's atacticity, we ran simulations of 27 unique AA single chains in vacuum (from our 1,2-BD melt simulations, we found that this number of chains is sufficient to ensure that the ensemble average does not change with a larger number of chains, and thus is representative of a bulk sample). These simulations were run using the NVT ensemble (in which simulation box volume, temperature, and the number of molecules are constant) with a simulation box large enough to prevent the chain from interacting with its periodic images. All atomistic parameters for EO–1,2-BD copolymer are presented in Table 1, the final coarse-grained bond and angle parameters for this copolymer are provided in Table 2, and the atomistic and CG distribution functions are compared in Fig. 3. The EO–1,2-BD nonbonded cross-interaction parameters were obtained using modified Lorentz–Berthelot combining rules discussed in subsequent sections.
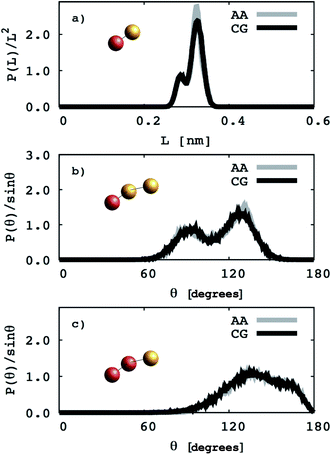 |
| | Fig. 3 Coarse grained (CG) and atomistic (AA) distributions for the poly(ethylene oxide)–1,2-polybutadiene (1,2-BD) block copolymer. The 1,2-BD coarse grain bead is shown in orange and EO bead is shown in red. Black lines represent coarse grained distributions and gray lines indicate the distributions derived from atomistic simulations. The data are obtained from simulations of a single chain in vacuum. The distributions of bond lengths between the 1,2-BD and EO beads are presented in (a). Bond angle distributions between one EO and two 1,2-BD, and two EO and one 1,2-BD beads are presented in (b) and (c), respectively. | |
EO–EE. Although EO solubility in water depends on temperature and molecular weight, a CG model can reproduce the polymer's radius of gyration (an indicator of solvent quality) for a range of temperatures and molecular weights.38 Thus, we can use a CG model with only one EO bead type. We propose a simple but chemically specific EO–EE force field that combines parameters from previous work on poly(ethylene oxide)–poly(ethyl ethylene)22,23 and poly(ethylene oxide)–poly(ethylene).24,25,39 In this series of papers, the Klein group uses Iterative Boltzmann Inversion to derive harmonic bond and angle interactions, and in the more recent EO–EE papers, nonbonded interactions use Lennard-Jones type functions. Polymer–polymer interactions use the LJ9−6 function, where as water–water and polymer–water interactions use a model with exponent 12 for the repulsive and 4 for the attractive part (LJ12−4). These published simulations use five types of force sites: the hydrophilic/hydrophobic chain end, hydrophilic/hydrophobic repeats, and hydrophobic middle bead. Other papers on poly(ethylene oxide)–poly(ethylene) self-assembled structures have used models without a unique middle bead.24,39 We propose a simplified model for EO–EE with only two types of coarse-grained beads: one for each type of monomer. Parameters for the proposed model are provided in Table 3. We also tested whether the nonbonded cross-interaction parameters for this simplified model can be obtained using combining rules, and present the details of this analysis in the discussion section.
Table 3 Coarse grained parameters for poly(ethylene oxide)–poly(ethyl ethylene) (EO–EE) block copolymer membranes. The parameters proposed are based on the ones given by Srinivas17 and Shinoda.22,23 All non-bonded cross-interaction parameters are given by modified Lorentz–Berthelot combining rules with scaling factor λ = 0.3 (see eqn (11) and (12))
| Non-bonded bead |
LJm−n |
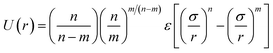
|
| ε (kcal mol−1) |
σ (Å) |
| EO |
LJ9−6 |
0.405 |
4.25 |
| EE |
LJ9−6 |
0.260 |
5.00 |
| W |
LJ12−4 |
0.895 |
4.37 |
| Bond |
U(L) = k(L − L0)2 |
| k (kcal mol−1 Å2) |
L0 (Å) |
| EO–EO |
4.520 |
2.970 |
| EO–EE |
3.229 |
3.354 |
| EE–EE |
3.179 |
3.348 |
| Angle |
U(θ) = k(θ − θ0)2 |
| k (kcal mol−1 rad−2) |
θ0 (degrees) |
| EO–EO–EO |
1.987 |
138 |
| EO–EO–EE |
1.788 |
146 |
| EO–EE–EE |
6.557 |
98 |
| EE–EE–EE |
10.332 |
102 |
Water. We considered a range of coarse-grained models for water, with differences in the number of water molecules in a CG force site and the repulsive and attractive exponents of the LJ-type potential.40 We chose a LJ12−4 model, and with three water molecules in one coarse-grained force site:| |
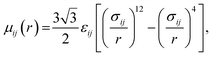 | (1) |
where εij is the depth of the potential well and the σij is the shortest distance at which the potential is zero. The Klein group uses this LJ12−4 model in later EO–ethylene simulations rather than the LJ6−4 coarse-grained water model used in earlier simulations of solvated EO–EE membranes.23,24,39 The LJ12−4 model yields a compressibility (0.605 GPa−1) that is closer to the experimental value (0.45 GPa−1) than the LJ6−4 model (1.044 GPa−1), while maintaining similar agreement for surface tension.24,40
Simulation setup. All simulations were performed using the LAMMPS simulation software.41 The atomistic 1,2-BD melt simulations were run using an ensemble with constant temperature, pressure, and number of atoms (the NPT ensemble). Temperature and pressure were set to T = 323 K and P = 1 atm using a Nose–Hoover thermostat and barostat with time constants of 50 fs and 500 fs respectively, and a time-step 0.5 fs. The atomistic simulations of single copolymer chains in vacuum used an NVT ensemble at the same temperature, and used the same time step and thermostat time constant, with a simulation box big enough to prevent interaction of the copolymer chain with its periodic images. The CG polymer melt simulations were run using an NPT ensemble (T = 323 K, P = 1 atm) with a time step of 4 fs, and a Nose–Hoover thermostat and barostat with time constants 400 and 4000 fs respectively.
2.2 Membrane simulations
For the CG membrane simulations, the initial configuration was a pre-assembled membrane with water. The membranes were hydrated with two water beads per EO bead for each system, which is comparable to the initial configuration from a previous study.23 Simulations were run in the NPT ensemble (T = 298.15 K, P = 1 atm) using a Nose–Hoover thermostat and barostats42 with time constants of 250 fs and 500 fs respectively. The time step used for all membrane simulations was 4 fs with the velocity-Verlet integrator. The cut-off value used for the non-bonded potential was 15 Å. The barostats in the lateral directions for co-polymer membrane are coupled (x and y directions in Fig. 1c). This approach, used for lipid membranes,21 provides a way to maintain the external stress tensor at zero and allows the area per lipid to fluctuate around a constant value. A plot showing the stress tensor fluctuating around zero for one of the polymer membranes is provided in the ESI (Fig. S7†). An alternative method is to use the NPAT ensemble, in which the constant area per chain (A) is chosen so the surface tension is zero.23 Both approaches are based on the same concept presented by Goetz and Lipowsky.43 We chose to couple the barostats in the lateral direction so that we can verify that our models reproduce the correct area per chain from experiments.
The area per chain (A) is a time average of the instantaneous cross-sectional area (Axy) normalized by the number of copolymers in one leaflet (Nl, where l = t, b, indicates top or bottom leaflet):
| |
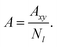 | (2) |
The membrane thickness (d) is an average of the out-of-plane distance between hydrophilic/hydrophobic junction beads belonging to the different leaflets:
| |
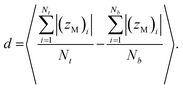 | (3) |
Here (
zM)
i indicates the
z coordinate (see
Fig. 1c) of the
ith copolymer junction bead in the upper or lower leaflet, and
Nt and
Nb are the numbers of the copolymers in each of the leaflets. Note that by “junction bead,” we mean the hydrophobic monomer bead bound to a hydrophilic bead, and that this junction bead has the same bonded and nonbonded parameters as the other hydrophobic beads in the chain. The thickness of the hydrophilic corona is calculated using the same equation, except that the average out-of-plane distance is calculated between the junction bead and the end bead of EO. The end bead of EO has the same bonded and non-bonded parameters as the other hydrophilic beads in the chain. All membrane simulations were run until the membrane thickness and area/chain converged to steady-state values, and the standard deviations for
d and
A are calculated from the instantaneous values that these variables take at each simulation output step.
We calculate the chain stretching s using eqn (4):
| |
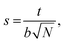 | (4) |
where
t is the thickness of a hydrophilic/hydrophobic monolayer (given by the difference between the
z-coordinates for each chain's end bead and junction bead, averaged over all simulation time steps and all chains),
N is a number of Kuhn monomers in the hydrophobic or hydrophilic block, and
b is the Kuhn length for the polymer of interest.
26,44 The denominator in
eqn (4) is the mean end-to-end distance for an unperturbed chain in a polymer melt:
44
To determine the number of Kuhn monomers per chain, we use the number-averaged molecular weight of the polymer chain Mn, and the Kuhn monomer mass M0:
| |
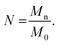 | (6) |
To represent the distribution of water, EO, and hydrophobic monomers in the z-direction (normal to the plane of the membrane), we calculate a normalized number density Pi(z) for each CG bead type i given by eqn (7):
| |
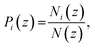 | (7) |
where
Ni(
z) is a time average of the number density of the CG bead of type with
z-coordinates been between
z and
z + Δ
z and
N(
z) is a total number of CG beads in the given slice. The bin width Δ
z used in this calculation was 1/500 of box length in the
z-direction.
2.3 Membrane thickness measurements
To obtain experimental values for EO–1,2-BD and EO–EE hydrophobic block thickness for ultra-short (Nhydrophobic < 40) polymer membranes, we synthesized four polymers (EO18–EE21, EO7–BD13, EO16–BD24, and EO24–BD34), prepared polymer vesicle solutions, imaged the vesicles using cryo-TEM, and measured the membrane thicknesses for a number of different vesicles for each polymer. EO–EE and EO–1,2-BD block copolymers were synthesized by anionic polymerization following a procedure based on that of Bates et al.45 To synthesize EO–1,2-BD rather than EO–EE, we skipped the hydrogenation step (shown in step two of Scheme 1 in Bates' paper45). Details of our thickness measurement procedure are given in ESI.† Area/chain for our BC membranes could not be measured directly, so we calculated this value from the membrane thickness and molecular volume using the assumption that the polymer is incompressible (as was done by Won et al.26).
3. Results and discussion
We organize our results into two main topics: first, we describe CG model parameters that reproduce the membrane thicknesses from experiments and previous simulations, then we examine the nanoscale details of the membrane structure that are more difficult to access experimentally. The first section includes comparison of EO–EE membrane thickness from our model to that of Srinivas and coworkers23 and to structures from cryo-TEM experiments,16,26 and comparison of EO–1,2-BD membrane thicknesses from our model to cryo-TEM measurements.16,26 We choose a combining rule for hydrophobic–hydrophilic and hydrophobic–water cross-interactions that allows us to reproduce these results. The second section includes information on the scaling of membrane thickness and area/chain with degree of polymerization, chain stretching, and membrane hydration, and comparisons to experimental data where available.
3.1 CG EO–EE and EO–1,2-BD models
Our goal is to test whether we can reproduce biomimetic structures with a simplified model using only two different bead types (one for each monomer) and Lennard-Jones type functions for nonbonded interactions (which might allow us to obtain nonbonded interactions using a simple combining rule46,47). Our first step is to test whether a two-bead model can reproduce the membrane thickness and area/chain data that Srinivas et al. report for their five-bead EO–EE model.23 In Fig. 4 we compare thickness and area/chain predicted by these two models for EO40EE37 and EO19EE18 membranes. We see good agreement between the model predictions, and conclude that this “reduced” model can predict reasonable values for membrane thicknesses and area per chain.
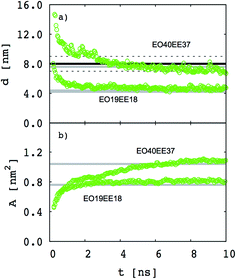 |
| | Fig. 4 Equilibration of the membrane thicknesses and area per chain for the “reduced” (two-bead) EO–EE model. Grey lines (published simulations data17) and a black line (published experiment data16,26) are shown for comparison. Dotted lines indicate experimental uncertainty. | |
To further simplify the EO–EE and EO–1,2-BD membrane models, we test whether we can use Lorentz–Berthelot combining rules to obtain all nonbonded cross-interaction parameters. In Fig. 5, we plot the nonbonded cross-interaction potentials predicted by the LB combining rules (grey lines), and compare them to those from the two-bead model (black lines) using published parameters given in Table 3. We see good agreement between the potential functions for hydrophilic/water cross-interactions (Fig. 5a), but note that the Lorentz–Berthelot combining rules overestimate the potential well depth for hydrophobic/water or hydrophobic/hydrophilic cross-interactions (Fig. 5b and c).
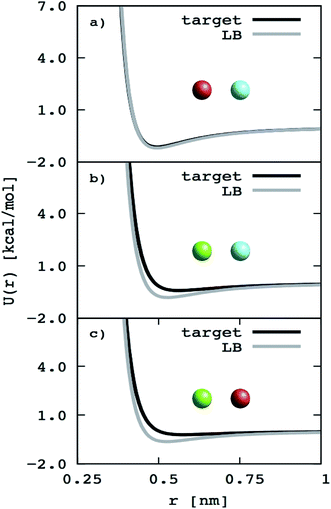 |
| | Fig. 5 Non-bonded cross-interaction potentials for the “reduced” EO–EE model compare to the ones given with use of the Lorentz–Berthelot (LB) combining rules. The target potential functions (the nonbonded cross-interaction functions provided by Srinivas22,23 and Shinoda24,25) compared to the ones calculated using Lorentz–Berthelot combining rules. | |
Therefore, we screened a range of combining rules to test if one or more of them can reproduce the available experimental data for EO–1,2-BD and EO–EE membrane thicknesses. These combining rules predict non-bonded cross-interactions for beads i and j from the self-interactions parameters εii/jj and σii/jj (the depth of the potential well and the shortest distance at which the potential is zero, respectively). The methods we test are 6th power combining rules:47
| |
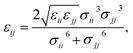 | (8) |
| |
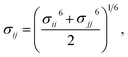 | (9) |
Halgren combining rules (Ha)46
| |
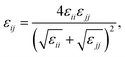 | (10) |
| |
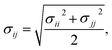 | (11) |
and Lorentz–Berthelot with a scaling factor
λ (LB
λ):
| |
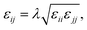 | (12) |
| |
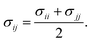 | (13) |
This scaling factor approach has been reported previously for the various coarse-grained systems including alkanes, perfluoroalkanes, gasses, polymer solutions, and lipids.48–52 In Fig. 6, we compare the membrane thicknesses obtained using these combining rules to experimental values. For the three EO–BD and two EO–EE membranes for which we have cryo-TEM data, we obtain the best agreement between simulation and experiment using Lorentz–Berthelot combining rules with scaling factor 0.3. In addition, all membrane thicknesses from simulations using this combining rule matched the experimental values within the uncertainty of the cryo-TEM measurements (about 1 nm). Thus, we decided to use this set of combining rules (Lorentz–Berthelot for hydrophilic/water, Lorentz–Berthelot with scaling factor 0.3 for hydrophobic/hydrophilic and hydrophilic/water) for all further simulations. We note, however, that simulations using scaling factors 0.2 and 0.4 also match the experimental data within this uncertainty, giving our ε parameters for hydrophobic/hydrophilic and hydrophobic/water nonbonded cross-interactions an uncertainty of about 33%. Parameters for this model are given in Table 2 (bonded parameters and non-bonded self-interaction parameters for EO–1,2-BD) and Table 3 (bonded parameters and non-bonded self-interaction parameters for EO–EE). A similar comparison for experimental vs. simulated area/chain is shown in ESI (Fig. S9†). Because the experimental area/chain values are calculated from the membrane thickness and molecular volume, the area/chain and membrane thickness results unsurprisingly suggest using the same scaling factors.
 |
| | Fig. 6 Membrane thicknesses for all combining rules considered. These combining rules (given by eqn (8)–(13)) are: 6th power combining rules (6th), Halgren combining rules (Ha), Lorentz–Berthelot Combining rules (LB), and Lorentz–Berthelot combining rules with a scaling factor λ between 0.1 and 0.9 (LBλ). Target values (measurements from cryo-TEM images) are shown as gray lines with dashed lines indicating the experimental uncertainty. A vertical dashed red indicates the combining rules we decided to choose to obtain the non-bonded cross-interactions parameters for any pairs of the hydrophobic/hydrophilic or hydrophobic/water beads. The experimental data for EO40EE37 are the ones reported by Bates et al.16,26 | |
An interesting question for further research would be whether this CG force field parameterization method could be applied to other block copolymers. Given that scaling factor methods have been used to develop CG force fields for a variety of materials,48–52 we consider this a strong possibility. However, we also note that the models we combined were derived in a similar way: CG beads were parameterized such that the bead's center is placed at the monomer center of mass, the CG models are parameterized to reproduce structural distribution functions from OPLS/AA simulations, and self-interaction parameters for each polymer were based on AA melt simulations.22–24 Provided that these similarities are maintained in the force fields combined, our methods might be used to study membranes made from polymers structurally similar to EO–1,2-BD and EO–EE, such as 1,2-polyisoprene–poly(ethylene oxide). These methods might also be applied in creating CG models for other amphiphilic block copolymer such as poly(styrene)–poly(ethylene oxide) and poly(dimethyl siloxane)–poly(2-methyl-2-oxazoline). However, we would use caution in applying this approach to amphiphilic block copolymers in which the hydrophobic block has specific interactions with water such as hydrogen bonding, as in poly(propylene oxide)–poly(ethylene oxide);53 a LBλ combining rule may not reproduce these specific interactions. In addition, the required scaling factor may be influenced by the Flory–Huggins parameter describing the interactions between the two polymer blocks.54 With these caveats in mind, however, our force field parameterization procedure could provides a simple (but approximate) method for creating block copolymer force fields.
3.2 Scaling rules for membrane thickness and area/chain as a function of molecular mass
It has been shown that membrane thickness, d, can be described by the power law:16,23where Mn is the number-averaged molecular weight of the polymer chain and α is a scaling exponent. Moreover, assuming membrane incompressibility, we can also express area per chain, A, as a function of Mn as:
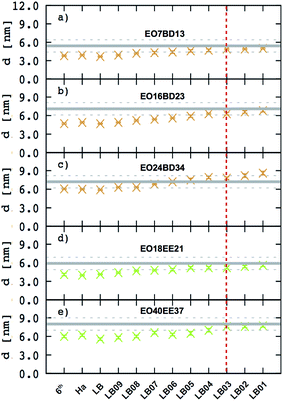
In Fig. 7. we present membrane thickness and area/chain data from our simulations,23 our cryo-TEM experiments (see ESI†), and other authors' cryo-TEM experiments.16,26 All values used in this figure are given in Table 4. The value of the scaling exponent informs us about molecular weight dependence of the given quantity (membrane thickness or area per chain): the larger the exponent the stronger the dependence. We know that for an ideal chain, one can expect a membrane thickness scaling exponent α = 0.5, and thus an area/chain scaling exponent 1 − α = 0.5 assuming that the polymer is incompressible.16,55 On the other hand, a chain in the strong segregation limit stretches to minimize hydrophobic–water contacts, and would have a predicted scaling exponent α = 2/3.16 Therefore, we would expect EE and 1,2-BD to have α in the range 0.5 to 0.66 (0.5 corresponds to a random coil, 0.6 to a polymer in a good solvent, and 0.66 to the strong segregation limit).16,56,57 Previous studies have proposed a scaling exponent of 0.5 for both copolymers,16,26 although it was suggested that the scaling exponent might be higher for low molecular weight copolymers.23 Because lower molecular weight copolymer membranes (hydrophobic block length about 12–40 monomers for a diblock copolymer) are important for protein incorporation, we wanted to examine this suggestion and measure the membrane thicknesses for three lower molecular weights copolymers (EO7BD13, EO16BD23 and EO18EE21). Using EO–EE and EO–1,2-BD data from our simulations and experiments, as well as experimental data from previous studies, we obtain a scaling exponent α = 0.6 ± 0.04. We apply the reduced chi-square statistical test58 to this fit, and obtain a chi-square value of 0.75, indicating that this scaling rule adequately describes the data within the experimental uncertainty (about 1 nm for membrane thickness). Thus, we do not need to fit separate scaling rules for each polymer or for different molecular weight ranges in order to describe the scaling behavior. We note that α = 0.6 is within the range expected from theory and previous experiments (0.5–0.66),16,26,55 suggesting that we have tuned our model to correctly reproduce polymer membrane structure. Finally, we note that the data presented in Fig. 7 and Table 4 indicate that the hydrophilic fraction fEO may slightly influence the scaling exponent α: most of the data points (fEO = 0.3–0.4) have minimal deviations from α = 0.6 trend line, where as the few points with fEO < 0.3 have larger deviations.
 |
| | Fig. 7 Membrane thickness (d) and area per chain (A) as a function of the hydrophobic block molecular mass. The hydrophobic thickness of block copolymer membrane (a) and area per chain (b) are shown on a log–log scale for both poly(ethylene oxide)–poly(ethyl ethylene) (EO–EE, green) and poly(ethylene oxide)–poly(1,2-butadiene) (EO–1,2-BD, orange). Empty circles represent data from our simulations, circles filled in black represent our experimental data, and circles filled in gray represent experimental data reported in ref. 16 and 26. Black lines indicate the best fit to the data, while gray lines indicate a random coil scaling behavior. | |
Table 4 Block copolymer membranes structural properties. All block copolymer membrane simulated along with thicknesses given from cryo-TEM measurements (indicated in brackets)
| Copolymer |
fEO |
Area per chain [nm2] |
Hydrophobic |
Hydrophilic |
| Thickness [nm] |
End-to-end distance [nm] |
s [] |
End-to-end distance [nm] |
s [] |
| The experimental data reported by Bates et al.16,26 |
| EO9BD10 |
0.36 |
0.59 ± 0.02 |
3.4 ± 0.1 |
1.70 ± 0.04 |
0.950 ± 0.022 |
1.81 ± 0.02 |
1.079 ± 0.012 |
| EO7BD13 |
0.25 |
0.51 ± 0.02 |
4.9 ± 0.1 |
2.29 ± 0.05 |
1.065 ± 0.023 |
0.97 ± 0.02 |
0.691 ± 0.014 |
| |
|
(0.45 ± 0.22) |
(5.4 ± 1.0) |
|
|
|
|
| EO13BD12 |
0.40 |
0.66 ± 0042 |
4.0 ± 0.1 |
2.03 ± 0.05 |
0.944 ± 0.023 |
2.24 ± 0.04 |
1.219 ± 0.022 |
| EO16BD15 |
0.40 |
0.73 ± 0.02 |
4.3 ± 0.1 |
2.25 ± 0.06 |
0.974 ± 0.026 |
2.68 ± 0.03 |
1.263 ± 0.014 |
| EO19BD18 |
0.39 |
0.80 ± 0.02 |
4.8 ± 0.1 |
2.51 ± 0.07 |
0.992 ± 0.030 |
3.17 ± 0.03 |
1.370 ± 0.013 |
| EO18BD21 |
0.34 |
0.73 ± 0.02 |
5.1 ± 0.1 |
2.56 ± 0.06 |
0.936 ± 0.040 |
3.11 ± 0.05 |
1.381 ± 0.022 |
| EO16BD23 |
0.30 |
0.77 ± 0.02 |
6.3 ± 0.2 |
3.05 ± 0.08 |
1.066 ± 0.028 |
2.66 ± 0.05 |
1.253 ± 0.024 |
| |
|
(0.65 ± 0.05) |
(7.1 ± 1.0) |
|
|
|
|
| EO24BD34 |
0.31 |
0.90 ± 0.02 |
7.8 ± 0.1 |
3.8 ± 0.1 |
1.092 ± 0.029 |
3.78 ± 0.04 |
1.454 ± 0.015 |
| |
|
(0.92 ± 0.06) |
(7.2 ± 1.0) |
|
|
|
|
| EO10EE9 |
0.35 |
0.64 ± 0.02 |
3.12 ± 0.08 |
1.55 ± 0.03 |
0.999 ± 0.019 |
2.01 ± 0.03 |
1.198 ± 0.017 |
| EO7EE13 |
0.25 |
0.57 ± 0.02 |
4.4 ± 0.1 |
2.04 ± 0.04 |
1.094 ± 0.022 |
1.23 ± 0.02 |
0.876 ± 0.014 |
| EO13EE12 |
0.39 |
0.72 ± 0.02 |
3.6 ± 0.1 |
1.84 ± 0.04 |
1.027 ± 0.022 |
2.49 ± 0.04 |
1.301 ± 0.021 |
| EO16EE15 |
0.39 |
0.80 ± 0.02 |
4.2 ± 0.1 |
2.13 ± 0.06 |
1.064 ± 0.030 |
2.90 ± 0.05 |
1.366 ± 0.024 |
| EO19EE18 |
0.39 |
0.83 ± 0.02 |
4.6 ± 0.1 |
2.36 ± 0.06 |
1.076 ± 0.027 |
3.28 ± 0.05 |
1.418 ± 0.022 |
| EO18EE21 |
0.34 |
0.81 ± 0.02 |
5.2 ± 0.2 |
2.59 ± 0.07 |
1.093 ± 0.030 |
3.02 ± 0.04 |
1.341 ± 0.018 |
| |
|
(0.74 ± 0.06) |
(5.9 ± 1.0) |
|
|
|
|
| EO16EE23 |
0.30 |
0.81 ± 0.02 |
5.9 ± 0.2 |
2.9 ± 0.1 |
1.169 ± 0.040 |
2.91 ± 0.03 |
1.371 ± 0.014 |
| EO24EE34 |
0.30 |
0.96 ± 0.02 |
7.5 ± 0.2 |
3.7 ± 0.1 |
1.227 ± 0.033 |
3.93 ± 0.05 |
1.512 ± 0.019 |
| EO40EE37 |
0.40 |
1.04 ± 0.03 |
7.6 ± 0.2 |
3.85 ± 0.07 |
1.224 ± 0.022 |
5.3 ± 0.1 |
1.579 ± 0.030 |
| |
|
(1.0 ± 0.1)a |
(8.0 ± 1.0)a |
|
|
|
|
3.3 Stretching of hydrophobic and hydrophilic chains compared to the random coil configuration
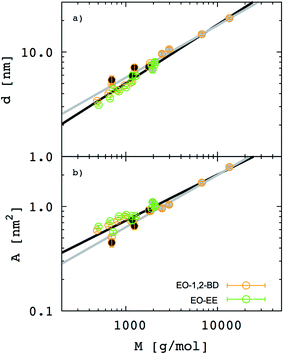
Besides the inferences we can make about chain stretching from the scaling exponents, we calculated degree of chain stretching directly using eqn (4)–(6). Values of the stretching parameter s for the hydrophobic and hydrophilic blocks of each simulated polymer membrane are given in Table 4 and plotted as function of area per chain in Fig. 8. We see that all hydrophobic blocks have s in the range 1 to 1.2 independent on the area per chain. This observation is consistent with our prediction of the scaling exponent α = 0.6 and with similar stretching parameters for higher molecular weight EO–EE and EO–BD diblock and triblock copolymer membranes examined by Bates et al.26
 |
| | Fig. 8 Stretching parameters of the hydrophobic and hydrophilic blocks compared to a random coil configuration. The stretching parameters for (a) hydrophobic and (b) hydrophilic chains are shown as a function of area per chain. 1,2-BD stands for 1,2-polybutadiene (orange), EE for poly(ethyl ethylene) (green), and EO for poly(ethylene oxide) (red). Empty circles represent data for all EO–1,2-BD membranes, whereas filled circles for all EO–EE ones. Dashed lines indicate the value for an ideal chain in the random coil configuration. | |
For EO, the degree of stretching varies significantly, from s ≤ 1 to s ≥ 1.5. To interpret this stretching, we consider the similarities between the EO corona and a tethered polymer brush (a well-studied system in polymer physics).55,59–64 Because the EO chains are tightly packed in the plane of the membrane (A/chain is 9–26% of the value for a random coil, A0 ∼ b2N), we can reasonably expect the EO chains to form a brush stretched in the z direction.55,59 Our EO coronas are not exactly like polymer brushes: for instance, the EO–hydrophobic junctions are mobile rather than having a fixed grafting density, and there is an energetic penalty for hydrophobic–water interactions, where as polymer brush theories do not consider water–substrate interactions.55,61 Nonetheless, we can show that our corona thickness is on the same order of magnitude as predicted by the simple polymer brush scaling theory of Alexander and De Gennes (see ESI†).59–62 Thus, although the trend shown in Fig. 8b) seems counterintuitive at first (we would expect stretching to decrease as A/chain increases for a polymer brush), we can explain this result on the grounds that larger A/chain corresponds to longer polymer chains, so that A/A0 is smaller and these chains are more stretched. We investigate the chain stretching and membrane structure further using the density profiles for polymer and water concentration in the membrane.
3.4 Membrane density profiles
In Fig. 9 (for EO–1,2-BD) and Fig. 10 (for EO–EE), we present density profiles for the five membranes for which we also have thickness measurements from cryo-TEM. Previous CG simulations of EE–EO membranes23 show an increase in the interdigitation of the membrane leaflets for longer polymer chains. To see whether our minimalistic models reproduce this trend, we calculate the density profiles for the hydrophobic chain ends separately (shown in purple in Fig. 9 and 10). We see a broadening of the end bead distributions with increasing molecular weight for both EO–EE and EO–1,2-BD membranes, consistent with the expected increase in interdigitation.
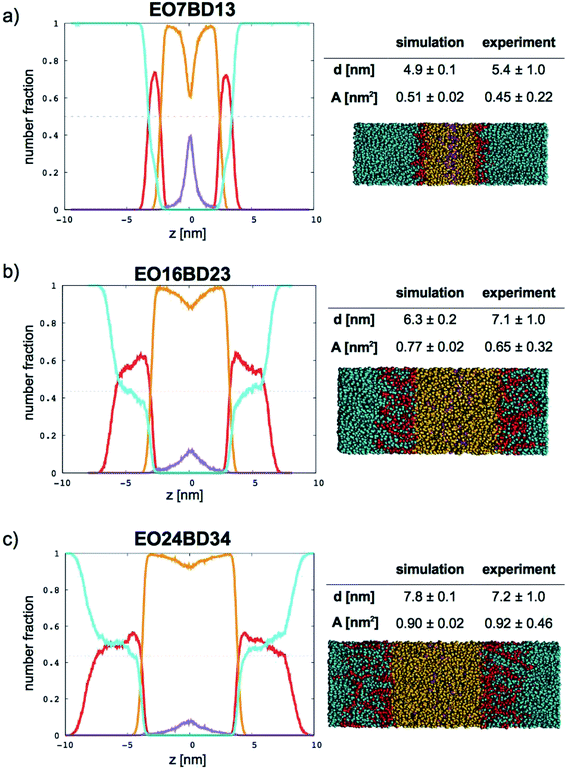 |
| | Fig. 9 Number fraction profiles for poly(ethylene oxide)–1,2-polybutadiene membranes. The calculated profiles for each EO–1,2-BD membrane are shown at left, and membrane simulation snapshots and structural parameters are shown at right. Colors used for each bead type are the same in the number density profiles and snapshots: water (cyan), EO (red), 1,2-BD (orange), and 1,2-BD end bead (purple). 1,2-BD end beads are shown separately to illustrate leaflet interdigitation. | |
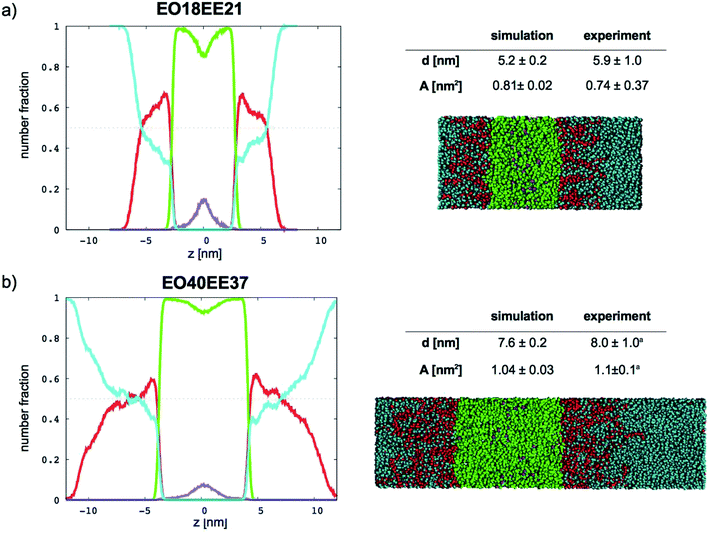 |
| | Fig. 10 Number fraction profiles for poly(ethylene oxide)–poly(ethyl ethylene) membranes. The calculated profiles for each EO–EE membrane are shown at left, and membrane simulation snapshots and structural parameters are shown at right. Colors used for each bead type are the same in the number density profiles and snapshots: water (cyan), EO (red), EE (green), and EE end bead (purple). EE end beads are shown separately to illustrate leaflet interdigitation. aThe experimental data reported by Bates et al.16,26 | |
Further, using the number density profiles we calculate for the CG water beads, we can also observe the hydration level of the simulated membranes. The water density profiles we calculated for EO–1,2-BD membranes are in good agreement with density profiles proposed based on X-ray scattering structure factors and TEM images of EO–1,2-BD vesicles.63 The authors of this X-ray and TEM study estimated that there should be three water molecules per EO monomer in the corona of the EO–1,2-BD vesicles. This is consistent with our membrane density profiles, which show that there is on average one coarse-grained water bead per coarse-grained EO bead in the corona (one CG water bead represents 3 water molecules and one CG EO bead represents an EO monomer). The density profiles also show that the EO corona is more concentrated at the interface between EO and the hydrophobic polymer (except for the shortest EO chain), consistent with experimental findings that the corona collapses to protect the hydrophobic block.63,64 The water density profile also shows that the water concentration at the hydrophobic–water interface is greater for longer chains: about 0.3 EO24–BD34 and about 0.15 for EO7–BD13. The change in hydration level can be explained in terms of the predicted area per polymer chain: a higher degree of polymerization leads to a larger area/chain, and thus greater possible hydration of the corona. However, the interface in which the hydrophobic block and water coexist is about the same thickness (roughly 1 nm) for all membranes examined, suggesting that the thickness (but not the water content) of this interface is independent of degree of polymerization. This is similar to the structure of a lipid bilayer, which has approximately 4 nm total thickness65 and a water-free region about 2 nm thick (obtained from X-ray and neutron scattering),66 and thus a 1 nm thick interface region where water and lipid coexist. Thus, all polymer membranes with thickness at least 5 nm will retain a water-free region with thickness at least 3 nm, compared to 2 nm for a lipid bilayer.66 It has been shown via mean-field theory that to avoid unfavorable hydrophobic–water contacts, a thick polymer membrane must compress so that its hydrophobic thickness matches that of an incorporated transmembrane protein67 (which will be similar to that of the lipid bilayer), despite the entropic penalty that such compression entails. Based on our results for both total membrane thickness and thickness of the water-free region, it thus appears that even the smallest block copolymer currently used for membrane protein incorporation (EO7–BD13) must compress slightly to accommodate transmembrane proteins, and that some of the thinner membranes we simulated could be even more suitable for protein incorporation (see Table 4).
4. Conclusions
We have developed CG MD models for two biomimetic-membrane-relevant block copolymers, EO–EE and EO–1,2-BD. These models use one type of CG bead for each monomer (rather than requiring separately parameterized end or junction beads), and all non-bonded interactions are calculated using a Lennard-Jones-like form. We chose a combining rule for the hydrophobic/hydrophilic and hydrophobic/water nonbonded cross-interactions such that our simulations reproduce experimental values for membrane thickness (within the experimental resolution of 1 nm) measured in our lab and by Bates et al.16,26. Self-assembled membrane simulations in water used an NPT ensemble in which pressure-coupling in the plane of the membrane ensures tensionless conditions. Consequently, area per chain is not required as an input parameter for setting up the simulations, and can be an additional property calculated from the simulation trajectories and compared to experimental values. We chose a CG water model that correctly reproduces not only density and surface tension, but also compressibility, allowing the simulations to more accurately reproduce the membrane structure.
We determine that membrane thickness can be related to molecular weight using a power law with scaling exponent 0.6 ± 0.04. This scaling relationship adequately describes the available data for both EO–EE and EO–1,2-BD membranes with hydrophobic block degree of polymerization Nphob = 10–40. Thus, the scaling behavior for membrane thickness and area per chain appears (within the experimental resolution) to be the same for both polymers despite that EE is more hydrophobic than 1,2-BD. This scaling correlation can be used to approximately predict the EE or 1,2-BD block length that will best match a protein's hydrophobic thickness, and thus require the least deformation of the polymer to incorporate the protein.67
Calculated stretching parameters indicate that EE and 1,2-BD polymers have about the same degree of stretching for the hydrophobic block, consistent with their common scaling exponent for membrane thickness. Moreover, we show that stretching of the EO polymers increases with increasing area per chain, which corresponds to increasing hydration of the EO corona.
Based on the calculated density profiles, we observe an increase in hydrophobic leaflet interdigitation at higher molecular weight, consistent with previous simulations.23 We also observe that the EO in the hydrophilic corona is most concentrated near the hydrophilic/hydrophobic polymer interface, in good agreement with density profiles predicted for the EO brushes on EO–1,2-BD vesicles using X-ray scattering structure factors and TEM images.63
This approach has the limitations, e.g. because end beads are not taken into account in the proposed models it might be difficult to capture possible changes in the aggregate morphology due to the end groups, observed in some studies.68 Nonetheless, our results indicate that this simple representation of the block copolymer is sufficient to reproduce (and provide a molecular-scale perspective on) structural data important for applications, such as the membrane thickness and the hydration and hydrophobicity of the membrane environment.
Conflicts of interest
There are no conflicts of interest to declare.
Acknowledgements
J. K. M. acknowledges financial support from the US Department of Energy, Office of Advanced Scientific Computing; grant number DE-FG02-02ER25535. MK acknowledges support from the National Science Foundation, grant number 1552571. We thank Mikolaj Kowalik for technical assistance and providing helpful comments on the manuscript.
References
- J. Clarke, H.-C. Wu, L. Jayasinghe, A. Patel, S. Reid and H. Bayley, Continuous base identification for single-molecule nanopore DNA sequencing, Nat. Nanotechnol., 2009, 4, 265 CrossRef CAS PubMed.
- T. Karamitros, I. Harrison, R. Piorkowska, A. Katzourakis, G. Magiorkinis and J. L. Mbisa, De Novo Assembly of Human Herpes Virus Type 1 (HHV-1) Genome, Mining of Non-Canonical Structures and Detection of Novel Drug-Resistance Mutations Using Short- and Long-Read Next Generation Sequencing Technologies, PLoS One, 2016, 11, e0157600 Search PubMed.
- S. Mura, J. Nicolas and P. Couvreur, Stimuli-responsive nanocarriers for drug delivery, Nat. Mater., 2013, 12, 991 CrossRef CAS PubMed.
- M. Kumar, M. Grzelakowski, J. Zilles, M. Clark and W. Meier, Highly permeable polymeric membranes based on the incorporation of the functional water channel protein Aquaporin Z, Proc. Natl. Acad. Sci. U. S. A., 2007, 104, 20719 CrossRef CAS PubMed.
- P. S. Zhong, T. S. Chung, K. Jeyaseelan and A. Armugam, Aquaporin-embedded biomimetic membranes for nanofiltration, J. Membr. Sci., 2012, 407, 27 CrossRef.
- C. Y. Tang, Y. Zhao, R. Wang, C. Hélix-Nielsen and A. G. Fane, Desalination by biomimetic aquaporin membranes: review of status and prospects, Desalination, 2013, 308, 34 CrossRef CAS.
- D. E. Discher, V. Ortiz, G. Srinivas, M. L. Klein, Y. Kim, D. Christian, S. Cai, P. Photos and F. Ahmed, Emerging applications of polymersomes in delivery: from molecular dynamics to shrinkage of tumors, Prog. Polym. Sci., 2007, 32, 838 CrossRef CAS PubMed.
- P. Tanner, P. Baumann, R. Enea, O. Onaca, C. Palivan and W. Meier, Polymeric vesicles: from drug carriers to nanoreactors and artificial organelles, Acc. Chem. Res., 2011, 44, 1039 CrossRef CAS PubMed.
- S. Egli, M. G. Nussbaumer, V. Balasubramanian, M. Chami, N. Bruns, C. Palivan and W. Meier, Biocompatible functionalization of polymersome surfaces: a new approach to surface immobilization and cell targeting using polymersomes, J. Am. Chem. Soc., 2011, 133, 4476 CrossRef CAS PubMed.
- M. Kumar, J. E. Habel, Y.-x. Shen, W. P. Meier and T. Walz, High-density reconstitution of functional water channels into vesicular and planar block copolymer membranes, J. Am. Chem. Soc., 2012, 134, 18631 CrossRef CAS PubMed.
- Y.-x. Shen, P. O. Saboe, I. T. Sines, M. Erbakan and M. Kumar, Biomimetic membranes: a review, J. Membr. Sci., 2014, 454, 359 CrossRef CAS.
- Technologies, O. N., 2017, vol. 2017.
- Aquaporin A/S, Aquaporin Inside Reverse Osmosis Products, online early access, https://aquaporin.dk/technology/biomimetic-membranes/, accessed November 9, 2017.
- M. Grit and D. J. Crommelin, Chemical stability of liposomes: implications for their physical stability, Chem. Phys. Lipids, 1993, 64, 3 CrossRef CAS PubMed.
- B. M. Discher, Y.-Y. Won, D. S. Ege, J. C. Lee, F. S. Bates, D. E. Discher and D. A. Hammer, Polymersomes: tough vesicles made from diblock copolymers, Science, 1999, 284, 1143 CrossRef CAS PubMed.
- H. Bermudez, A. K. Brannan, D. A. Hammer, F. S. Bates and D. E. Discher, Molecular weight dependence of polymersome membrane structure, elasticity, and stability, Macromolecules, 2002, 35, 8203 CrossRef CAS.
- D. E. Discher and A. Eisenberg, Polymer vesicles, Science, 2002, 297, 967 CrossRef CAS PubMed.
- D. W. Van Krevelen and K. Te Nijenhuis, Properties of polymers: their correlation with chemical structure; their numerical estimation and prediction from additive group contributions, Elsevier, 2009 Search PubMed.
- R. F. Fedors, A method for estimating both the solubility parameters and molar volumes of liquids, Polym. Eng. Sci., 1974, 14, 147 CAS.
- G. Milano and F. Müller-Plathe, Mapping atomistic simulations to mesoscopic models: a systematic coarse-graining procedure for vinyl polymer chains, J. Phys. Chem. B, 2005, 109, 18609 CrossRef CAS PubMed.
- M. Doxastakis, V. G. Sakai, S. Ohtake, J. Maranas and J. De Pablo, A molecular view of melting in anhydrous phospholipidic membranes, Biophys. J., 2007, 92, 147 CrossRef CAS PubMed.
- G. Srinivas, J. C. Shelley, S. O. Nielsen, D. E. Discher and M. L. Klein, Simulation of diblock copolymer self-assembly, using a coarse-grain model, J. Phys. Chem. B, 2004, 108, 8153 CrossRef CAS.
- G. Srinivas, D. E. Discher and M. L. Klein, Self-assembly and properties of diblock copolymers by coarse-grain molecular dynamics, Nat. Mater., 2004, 3, 638 CrossRef CAS PubMed.
- W. Shinoda, R. DeVane and M. L. Klein, Multi-property fitting and parameterization of a coarse grained model for aqueous surfactants, Mol. Simul., 2007, 33, 27 CrossRef CAS.
- W. Shinoda, R. DeVane and M. L. Klein, Coarse-grained molecular modeling of non-ionic surfactant self-assembly, Soft Matter, 2008, 4, 2454 RSC.
- Y.-Y. Won, A. K. Brannan, H. T. Davis and F. S. Bates, Cryogenic transmission electron microscopy (cryo-TEM) of micelles and vesicles formed in water by poly(ethylene oxide)-based block copolymers, J. Phys. Chem. B, 2002, 106, 3354 CrossRef CAS.
- E. Brini, E. A. Algaer, P. Ganguly, C. Li, F. Rodríguez-Ropero and N. F. van der Vegt, Systematic coarse-graining methods for soft matter simulations – a review, Soft Matter, 2013, 9, 2108 RSC.
- F. Müller-Plathe, Coarse-graining in polymer simulation: from the atomistic to the mesoscopic scale and back, ChemPhysChem, 2002, 3, 754 CrossRef.
- W. Noid, Perspective: Coarse-grained models for biomolecular systems, J. Chem. Phys., 2013, 139, 09B201_1 CrossRef PubMed.
- D. Reith, M. Pütz and F. Müller-Plathe, Deriving effective mesoscale potentials from atomistic simulations, J. Comput. Chem., 2003, 24, 1624 CrossRef CAS PubMed.
- M. J. Sippl, Boltzmann's principle, knowledge-based mean fields and protein folding. An approach to the computational determination of protein structures, J. Comput.-Aided Mol. Des., 1993, 7, 473 CrossRef CAS PubMed.
- W. L. Jorgensen and J. Tirado-Rives, The OPLS [optimized potentials for liquid simulations] potential functions for proteins, energy minimizations for crystals of cyclic peptides and crambin, J. Am. Chem. Soc., 1988, 110, 1657 CrossRef CAS PubMed.
- W. L. Jorgensen, D. S. Maxwell and J. Tirado-Rives, Development and testing of the OPLS all-atom force field on conformational energetics and properties of organic liquids, J. Am. Chem. Soc., 1996, 118, 11225 CrossRef CAS.
- O. Okada and H. Furuya, Molecular dynamics simulation of cis-1,4-polybutadiene. 1. Comparison with experimental data for static and dynamic properties, Polymer, 2002, 43, 971 CrossRef CAS.
- Accelrys Software Inc., Materials Studio Version 7.0, San Diego, 2013 Search PubMed.
- D. Fritz, V. A. Harmandaris, K. Kremer and N. F. van der Vegt, Coarse-grained polymer melts based on isolated atomistic chains: simulation of polystyrene of different tacticities, Macromolecules, 2009, 42, 7579 CrossRef CAS.
- V. Harmandaris, N. Adhikari, N. F. van der Vegt and K. Kremer, Hierarchical modeling of polystyrene: From atomistic to coarse-grained simulations, Macromolecules, 2006, 39, 6708 CrossRef CAS.
- S. Nawaz and P. Carbone, Coarse-graining poly(ethylene oxide)–poly(propylene oxide)–poly(ethylene oxide)(PEO–PPO–PEO) block copolymers using the MARTINI force field, J. Phys. Chem. B, 2014, 118, 1648 CrossRef CAS PubMed.
- B. G. Levine, D. N. LeBard, R. DeVane, W. Shinoda, A. Kohlmeyer and M. L. Klein, Micellization studied by gpu-accelerated coarse-grained molecular dynamics, J. Chem. Theory Comput., 2011, 7, 4135 CrossRef CAS PubMed.
- X. He, W. Shinoda, R. DeVane and M. L. Klein, Exploring the utility of coarse-grained water models for computational studies of interfacial systems, Mol. Phys., 2010, 108, 2007 CrossRef CAS.
- S. Plimpton, Fast Parallel Algorithms for Short-Range Molecular Dynamics, J. Comput. Phys., 1995, 117, 1 CrossRef CAS.
- W. G. Hoover, Canonical dynamics: equilibrium phase-space distributions, Phys. Rev. A, 1985, 31, 1695 CrossRef.
- R. Goetz and R. Lipowsky, Computer simulations of bilayer membranes: self-assembly and interfacial tension, J. Chem. Phys., 1998, 108, 7397 CrossRef CAS.
- L. Fetters, D. Lohse and R. Colby, in Physical properties of polymers handbook, Springer, 2007, p. 447 Search PubMed.
- M. A. Hillmyer and F. S. Bates, Synthesis and characterization of model polyalkane-poly(ethylene oxide) block copolymers, Macromolecules, 1996, 29, 6994 CrossRef CAS.
- P. A. Golubkov, J. C. Wu and P. Ren, A transferable coarse-grained model for hydrogen-bonding liquids, Phys. Chem. Chem. Phys., 2008, 10, 2050 RSC.
- M. Waldman and A. T. Hagler, New combining rules for rare gas van der Waals parameters, J. Comput. Chem., 1993, 14, 1077 CrossRef CAS.
- F. Cao, J. D. Deetz and H. Sun, Free Energy-Based Coarse-Grained Force Field for Binary Mixtures of Hydrocarbons, Nitrogen, Oxygen, and Carbon Dioxide, J. Chem. Inf. Model., 2017, 57, 50 CrossRef CAS PubMed.
- C. Colina, A. Galindo, F. Blas and K. Gubbins, Phase behavior of carbon dioxide mixtures with n-alkanes and n-perfluoroalkanes, Fluid Phase Equilib., 2004, 222, 77 CrossRef.
- M. Orsi, D. Y. Haubertin, W. E. Sanderson and J. W. Essex, A quantitative coarse-grain model for lipid bilayers, J. Phys. Chem. B, 2008, 112, 802 CrossRef CAS PubMed.
- P. Virnau, M. Müller, L. G. MacDowell and K. Binder, Phase behavior of n-alkanes in supercritical solution: a Monte Carlo study, J. Chem. Phys., 2004, 121, 2169 CrossRef CAS PubMed.
- P. Virnau, M. Müller, L. G. MacDowell and K. Binder, Phase separation kinetics in compressible polymer solutions: computer simulation of the early stages, New J. Phys., 2004, 6, 7 CrossRef.
- S. Chen, C. Guo, H.-Z. Liu, J. Wang, X.-F. Liang, L. Zheng and J.-H. Ma, Thermodynamic analysis of micellization in PEO–PPO–PEO block copolymer solutions from the hydrogen bonding point of view, Mol. Simul., 2006, 32, 409 CrossRef CAS.
- A. Chremos, A. Nikoubashman and A. Z. Panagiotopoulos, Flory-Huggins parameter χ, from binary mixtures of Lennard-Jones particles to block copolymer melts, J. Chem. Phys., 2014, 140, 054909 CrossRef PubMed.
- M. Rubinstein and R. H. Colby, Polymer physics, OUP Oxford, 2003 Search PubMed.
- P. J. Flory, Principles of polymer chemistry, Cornell University Press, 1953 Search PubMed.
- P.-G. De Gennes and T. A. Witten, Scaling Concepts in Polymer Physics, Cornell University Press, Ithaca, 1980 Search PubMed.
- W. Press, S. Teukolsky, W. Vetterling and B. Flannery, Numerical Recipes, The Art of Scientific Computing, Cambridge University Press, New York, 3rd edn, 2007 Search PubMed.
- S. Alexander, Adsorption of chain molecules with a polar head a scaling description, J. Phys., 1977, 38, 983 CAS.
- P. de Gennes, Conformations of polymers attached to an interface, Macromolecules, 1980, 13, 1069 CrossRef CAS.
- S. Milner, Polymer brushes, Science, 1991, 251, 905 CrossRef CAS PubMed.
- S. T. Milner, T. Witten and M. Cates, Theory of the grafted polymer brush, Macromolecules, 1988, 21, 2610 CrossRef CAS.
- T. P. Smart, O. O. Mykhaylyk, A. J. Ryan and G. Battaglia, Polymersomes hydrophilic brush scaling relations, Soft Matter, 2009, 5, 3607 RSC.
- Y.-Y. Won, H. T. Davis, F. S. Bates, M. Agamalian and G. Wignall, Segment distribution of the micellar brushes of poly(ethylene oxide) via small-angle neutron scattering, J. Phys. Chem. B, 2000, 104, 7134 CrossRef CAS.
- M. Luckey, Membrane Structural Biology with Biochemical and Biophysical Foundations, Cambridge University Press, Canada, 2008 Search PubMed.
- N. Kučerka, J. F. Nagle, J. N. Sachs, S. E. Feller, J. Pencer, A. Jackson and J. Katsaras, Lipid bilayer structure determined by the simultaneous analysis of neutron and X-ray scattering data, Biophys. J., 2008, 95, 2356 CrossRef PubMed.
- V. Pata and N. Dan, The effect of chain length on protein solubilization in polymer-based vesicles (polymersomes), Biophys. J., 2003, 85, 2111 CrossRef CAS PubMed.
- M. Maskos, Influence of the solvent and the end groups on the morphology of cross-linked amphiphilic poly(1,2-butadiene)-b-poly(ethylene oxide) nanoparticles, Polymer, 2006, 47, 1172 CrossRef CAS.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c7ra10573h |
| ‡ Contributed equally. |
|
| This journal is © The Royal Society of Chemistry 2017 |
 Open Access Article
Open Access Article *ade
*ade