Synthesis, crystal structure and phase transition of a Xe–N₂ compound at high pressure: experimental indication of orbital interaction between xenon and nitrogen

Abstract

The van der Waals compound Xe(N₂)₂ with a C15 Laves structure was successfully synthesised at pressures greater than 4.4 GPa. We found that, at 10 GPa, the structure reversibly transforms from a cubic to a tetragonal phase. Further compression results in changes of Xe–N compound, which could result in the enhancement of orbital interactions between the xenon and nitrogen atoms.

---

Noble gases are inert chemical species owing to their stable electronic configurations. Despite this, several noble gas compounds have been discovered as a result of reactions between large noble gas atoms (e.g. Kr and Xe) and other elements such as metals, hydrogen, oxygen, and halogens (e.g. F and Cl).^1–10 For example, XePtF₆¹ was reported as a noble gas compound in which xenon exhibits charge transfer. Later, Kr and Ar were discovered to form binary and ternary compounds (e.g. HArF,² KrF₂,³ and HKrF⁴) that show a remarkable chemical bonding character, similar to that of XePtF₆. The high-pressure technique is recognised as one of the most powerful tools for the exploration of novel noble gas compounds.^11–18 The compression of noble gases and other molecular species at gigapascal pressures successfully leads to the formation of van der Waals compounds (e.g. He(N₂)₁₁,^11,12 Ne₇(N₂)₆,¹³ ArO₂,¹⁴ Ar(O₂)₃,¹⁴ Ar(H₂)₂,¹⁵ Kr(H₂)₄,¹⁶ Xe(O₂)₂,¹⁴ and Xe(H₂)₈^17,18). The type of high-pressure van der Waals compound formed depends on the sizes of the noble gas atom and molecular species. For example, when the atomic radius of the noble gas is large, hydrogen-rich van der Waals compounds are formed.^15–18 In addition, more recently, Dewaele et al. reported the successful synthesis of novel xenon oxides (Xe₂O₅ and Xe₃O₂) via the direct chemical reaction of xenon and oxygen at nearly 100 GPa.¹⁹ The successful formation of noble gas compounds that show charge transfer or van der Waals bonding offer new insights into the chemistry and nature of unusual chemical bonding.

In this study, we focused on the Xe–N₂ system. In particular, we have studied the syntheses of Xe–N compounds under high pressure using a diamond anvil cell (DAC). Despite the fundamental interest in the chemical and physical properties of these compounds, high-pressure studies on the Xe–N₂ system have been limited.^20,21 In the only high-pressure study of the Xe–N₂ system up to 13 GPa, Kooi and Schouten reported the formation of a van der Waals Xe–N₂ compound;²¹ however, the crystal structure of this compound is unknown because they examined the Xe–N₂ system by high-pressure in situ Raman spectroscopy at pressures below 13 GPa. In contrast, very recent theoretical calculations have predicted the formation of XeN₆, involving chemical bonding between Xe and N at pressures greater than 146 GPa.²¹ This prediction is interesting because the binding energy of molecular nitrogen (N≡N) is very high, and the electronegativity of nitrogen is lower than those of oxygen and the halogens, even though the outermost electron orbital of xenon is more likely to be hybridised than those of the other noble gases. These experimental and advanced theoretical calculations indicate that high-pressure techniques are a powerful tool to understand the Xe–N₂ system, including the formation of novel Xe–N compounds. We have, therefore, conducted high-pressure experiments on the Xe–N₂ system, reaching pressures of approximately 70 GPa at room temperature using a DAC combined with high-pressure in situ X-ray diffraction and Raman scattering measurements. Using these techniques, we succeeded in the synthesis of a van der Waals compound Xe(N₂)₂ and observed its structural transition at high pressure. Furthermore, the orbital hybridization resulting in chemical bonding between Xe and N is discussed based on the experimental results from high-pressure in situ microscopy observations, X-ray diffraction measurements, and the vibrational modes of molecular nitrogen in the structure as determined by Raman spectroscopy.

Details of the experimental set-up and data analyses are described in the supplementary information. All X-ray diffraction peaks measured at 2.4 GPa were assigned to either Au, the Re gasket, or the cubic phase (S1, ESI†). The lattice parameter of the cubic phase was calculated to be 5.632(3) Å, which is similar to that of the face-centred cubic structure of pure xenon (a = 5.541 Å)^22,23 at a corresponding pressure. In contrast, vibrational frequencies corresponding to the stretching mode of molecular nitrogen²⁴ were detected by Raman spectroscopy (S2, ESI†). Thus, xenon is likely to form a face-centred cubic structure with molecular nitrogen incorporated into the lattice. The inclusion of nitrogen contributes to the expansion of the unit cell volume compared to that of pure xenon.

On further compression of the sample at 4.4 GPa, new diffraction peaks appeared in addition to those of the face-centred cubic phase of xenon^22,23 (S1, ESI†). All new peaks were indexed to the cubic symmetry phase with a lattice parameter of 9.294(2) Å. Furthermore, this cubic phase was found to belong to a face-centred cubic lattice (F-lattice) containing a d-glide plane, as determined by the following diffraction conditions: h = k = l = odd or even for all Miller indices and h + k = 4n (n is an integer) for hk0 (S3, ESI†). Thus, we concluded that, at pressures greater than 4.4 GPa, xenon reacts with molecular nitrogen to form a new cubic Xe–N₂ compound that is not simply a face-centred cubic phase of xenon with nitrogen molecules incorporated into the structure. In our experiments, we found it difficult to determine the precise ratio of xenon and nitrogen, although a previous high-pressure experiment on Xe–O₂ system¹⁴ offers useful information on the crystal structure of the newly synthesised cubic Xe–N₂ compound. In studies of the Xe–O₂ system, a van der Waals Xe(O₂)₂ compound in the space group Fd3̄m has been reported, and this structure can be regarded as a C15 Laves phase.¹⁴ The lattice parameter of the Xe(O₂)₂ compound at 3.7 GPa was calculated to be 9.20 Å, similar to that of the cubic Xe–N₂ compound. Thus, our results, together with the crystallographic parameters of Xe(O₂)₂, indicate that the Laves phase of Xe(N₂)₂ was successfully synthesised at room temperature on the compression of xenon and molecular nitrogen at pressures greater than 4.4 GPa. The synchrotron XRD profile of an experimental run is shown in Fig. 1, together with a schematic illustration of the crystal structure of Laves Xe(N₂)₂. Several peaks between 2300 and 2400 cm⁻¹ in the Raman spectrum of the compound were found, demonstrating the presence of molecular nitrogen, although the peak frequencies were found at lower wavenumbers than those of pure molecular nitrogen at a corresponding pressure (S2, ESI†). This result indicates that molecular nitrogen in Xe(N₂)₂ has a different vibrational energy due to its coexistence with xenon.

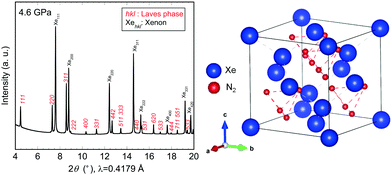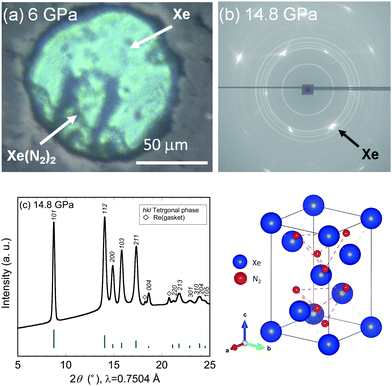
Fig. 1 Synchrotron X-ray diffraction profile of the Xe–N₂ system obtained at 4.6 GPa and room temperature, and a schematic illustration of the crystal structure of Laves Xe(N₂)₂.

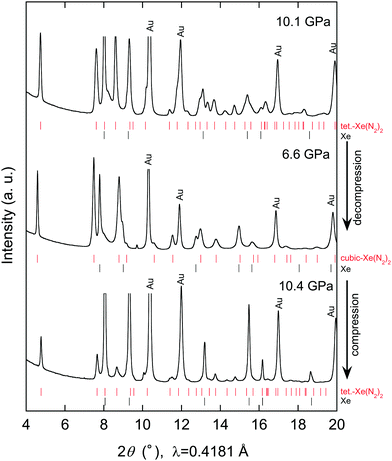
Further compression of the Laves Xe(N₂)₂ at room temperature resulted in changes in the XRD profile at a pressure of approximately 10 GPa. This result strongly suggests that either the Laves Xe(N₂)₂ structure transforms into a denser phase or that new Xe–N₂ compounds are formed. No X-ray diffraction peaks corresponding to nitrogen were observed, indicating that Xe(N₂)₂ did not dissociate. Thus, the new X-ray diffraction peaks likely arise from a denser Xe(N₂)₂ phase than that of the Laves phase. To understand this issue more clearly, we decreased the pressure to less than 1 GPa, and single crystals of excess xenon were grown by controlling the pressure, allowing the separation of the Laves Xe(N₂)₂ and xenon crystals, as shown in Fig. 2(a). The sample containing Laves Xe(N₂)₂ crystals and single crystals of xenon (although a small amount of nitrogen may also remain) was compressed at 14.8 GPa, and 2-D diffraction patterns were recorded on the charge-coupled device detector with the rotation of the DAC (Fig. 2(b)). The intense diffraction spots and the smooth Debye rings were indexed to the face-centred cubic lattice of xenon and the high-pressure Xe(N₂)₂ phase, respectively. The 2-D diffraction image was converted into a conventional 1-D profile after masking the intense diffraction spots arising from the xenon crystals (Fig. 2(c)). Peak indexing analysis of the new diffraction profile was carried out using dedicated software, and this analysis suggests a tetragonal unit cell setting with a = 5.787(1) and c = 9.272(2) Å at 14.8 GPa (S4, ESI†). The XRD profiles that were obtained at 10.1, 6.6, and 10.4 GPa during compression and decompression, are shown in Fig. 3. The absolute intensities and the intensity ratios of the reflections changed between the compression and decompression cycles (10.1 vs. 10.4 GPa).

Fig. 2 (a) Photograph of sample chamber taken at 6 GPa. (b) 2-D and (c) 1-D XRD profiles of tetragonal Xe(N₂)₂ acquired at 14.8 GPa, together with the simulated diffraction intensities of the HP-SiS₂ type structure (vertical bars), and a schematic illustration of the crystal structure of HP-SiS₂ type Xe(N₂)₂.

Fig. 3 XRD profile of Xe–N₂ compounds obtained at 10.1, 6.6, and 10.4 GPa during compression and decompression. Tick marks represent the Bragg peak positions of Xe(N₂)₂ and xenon at corresponding pressures.

Although kinetic effects during the phase transition must be considered, changes in diffraction intensity may arise from technical issues. For example, the compression and decompression processes resulted in the accumulation of deviatoric stress and consequent broadening of the diffraction peaks. Furthermore, the X-ray beam was focused, with a size smaller than that of the sample chamber: this might result in a change in the position of the X-ray irradiation spots between compression and decompression. Although some unassigned peaks remain, the observed diffraction peaks were well assigned to the Laves and tetragonal phases. Furthermore, we found that the phase transition was reversible with pressure.

With respect to the crystal structure of the high-pressure phase of Xe(N₂)₂, based on the crystal symmetry analysis, a tetragonal cell with an I-lattice satisfies the Miller-indexed peaks of the high-pressure phase. No significant changes were observed in the Raman spectra during the phase transition, suggesting that no significant changes to the molecular nitrogen in Xe(N₂)₂ occur. To evaluate the high-pressure phase of Xe(N₂)₂ in detail, AB₂-type compounds with tetragonal symmetry and a similar axial ratio were investigated from previously reported data. Consequently, we determined that the high-pressure phase of SiS₂ (HP-SiS₂)²⁵ is a plausible structural model for the high-pressure phase of Xe(N₂)₂, where the space group is I4̄2d and Xe and N₂ atomic positions correspond to those of Si and S, respectively. However, the exact coordination sites and the alignment and rotational direction of N₂ in the structure remain unclear. Thus, the atomic coordinates of N₂ are taken from the crystallographic structure of the HP-SiS₂ compound. The simulated diffraction peaks of the HP-SiS₂-type Xe(N₂)₂ are shown together with the experimental pattern in Fig. 2(c). It is difficult to account for the X-ray scattering from each nitrogen atom because the state of molecular nitrogen in the structure is unknown. Thus, the XRD profile was simulated assuming that X-rays are scattered from two nitrogen atoms at the same atomic site (equivalent to the scattering from a silicon atom). Despite these assumptions, the simulated and experimental XRD profiles are consistent. However, the fine details, such as the exact coordination sites, alignment, and rotational directions of N₂ in the structure, are important for a deep understanding of the crystal symmetry and its structural stability at high pressure. Therefore, further advanced experiments together with theoretical calculations are necessary to clarify these details.

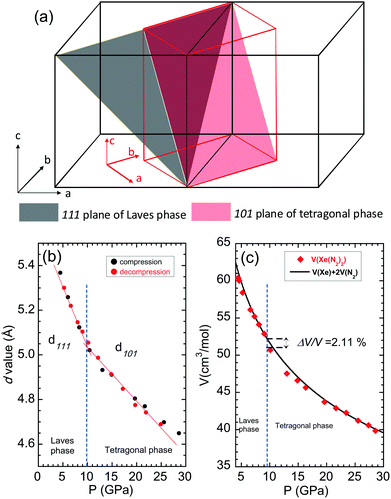
The phase transition in Xe(N₂)₂ from Laves to HP-SiS₂ phases is a martensitic transition (S5, ESI†). In the Laves phase, Xe has a diamond lattice structure, while N₂ has an isotropic tetrahedral (N₂)₄ structure, where each (N₂)₄ unit is corner-sharing (Fig. 1 and S5, ESI†). The atomic coordination of Xe in the HP-SiS₂-type phase remains almost same as that of the Laves phase, as clearly seen from the atomic arrangement, because the [110] direction of HP-SiS₂ phase corresponds to the [100] direction of the Laves phase (Fig. 4 and S5, ESI†). In contrast, in the tetragonal phase, N₂ is also located at the interstitial sites between Xe atoms, and the tetrahedral (N₂)₄ species are more distorted than those in the Laves phase. As shown in the schematic showing the relationship between the Laves and HP-SiS₂ phases (Fig. 4(a)), the 111 plane of the Laves phase is converted to 101 planes of the HP-SiS₂ phase on phase transition. The pressure dependences of the d-values of the 111 and 101 planes of the Laves and HP-SiS₂ phases, respectively, show no significant differences before and after the phase transition at around 10 GPa (Fig. 4(b)). The pressure dependences of lattice parameters, which are normalised to those at 10.9 GPa, show that the a-axis is more compressible than the c-axis (S6, ESI†). Furthermore, the tetragonal crystallinity (c/a) increases with increasing pressure (S6, ESI†). The pressure–volume (P–V) relationship of Xe(N₂)₂ is shown in Fig. 4. The solid line represents the P–V data for Xe + 2N₂ based on the equation of state determined from the high-pressure experiments.^22,23,26 The Laves phase has a lower unit cell volume than that of Xe + 2N₂, up to approximately 10 GPa. However, the volume difference between the Xe + 2N₂ and Laves Xe(N₂)₂ phases gradually decreases with increasing pressure. As the pressure increased beyond 10 GPa, Xe(N₂)₂ transformed into a denser crystal structure of the HP-SiS₂ type, which reduced the free energy. The volume reduction per chemical formula of Xe(N₂)₂ between the Laves and HP-SiS₂-type phases was calculated to be 2.11%.

Fig. 4 (a) Unit cell relationship between the cubic and tetragonal phases. (b) Pressure dependence of the d-values for 111 and 101 planes of the cubic and tetragonal phases, respectively. The solid lines are eye guides. (c) Pressure–volume relationship for X(N₂)₂ up to approximately 30 GPa. The solid line represents the equation of state for Xe + 2N₂ based on the high-pressure experiments.

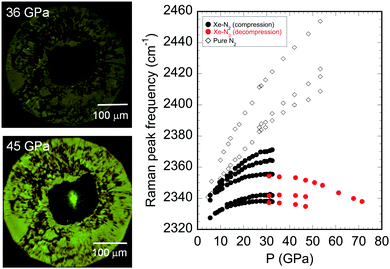
Based on recent theoretical calculations, xenon is expected to form XeN₆, forming chemical bonds between Xe and N at a pressure of 146 GPa.²¹ In this study, the van der Waals compound Xe(N₂)₂ was synthesised and a phase transition was observed on compression at room temperature. In addition, further compression to approximately 70 GPa yielded interesting results, even though the pressure was less than the theoretically predicted pressure for the formation of XeN₆. Fig. 5 shows photographs of the sample chamber used for the high-pressure irradiation of the sample with a semiconductor laser, which was used as the excitation source for the ruby fluorescence method. The photographs were taken through the filter is used for cutting the incident 405 nm laser beam. No anomalous behaviour was observed during sample irradiation with laser at 36 GPa, while intense fluorescence was observed when the pressure was increased to 45 GPa. This strong fluorescence made it difficult to measure the weak Raman peaks. The results of Raman spectroscopy demonstrate the pressure dependence of the Raman peak frequencies associated with the stretching vibrational modes of molecular nitrogen, which gradually became constant, and finally shifted to lower wavenumbers with increasing pressure (Fig. 4 and S7, ESI†).

Fig. 5 Photograph of the sample chamber taken through the filter used to cut the incident laser light (λ = 405 nm) at 36 and 45 GPa. Pressure dependence of Raman peak frequencies with respect to the stretching vibration mode of molecular nitrogen up to approximately 70 GPa. Above 40 GPa, some Raman peaks could not be easily detected due to the intense fluorescence from the sample.

The Raman peak frequency is strongly dependent on the bonding between nitrogen atoms (for example, N≡N (d_N≡N = ∼1.1 Å), N=N (d_N=N = 1.2–1.3 Å), and N–N (d_N–N = ∼1.4 Å)), and the Raman peak frequencies shift to lower wavenumbers with increasing separation (d) between the nitrogen atoms (ω_N–N = 700–800 cm⁻¹, ω_N=N = 1100–1300 cm⁻¹, and ω_N≡N = 2300–2400 cm⁻¹).^24,27,28 Thus, the constant decrease in the Raman peak frequencies likely corresponds to a constant increase in the atomic separation of molecular nitrogen with increasing pressure. In previous high-pressure experiments for the Xe–H₂ system, a shift to lower wavenumbers of the Raman peaks for the hydrogen stretching mode has also been observed, resulting from the weakening of the H–H bond and orbital hybridization between xenon and hydrogen atoms.¹⁷ Electron interactions, including charge transfer, have been reported based on the theoretical calculations on noble gas/halogen systems,²⁹ and these orbital interactions might also give rise to the strong fluorescence reported for polymeric molecules and amino acids.³⁰ Although no direct experimental evidence concerning the chemical bonding between xenon and nitrogen atoms was found in this study, the observed high fluorescence and anomalous pressure dependence of the Raman frequencies suggest an enhancement in the orbital interactions between xenon and nitrogen atoms, resulting from their increased proximity at high pressures. The changes in the Xe–N₂ compound at around 30–40 GPa are consistent with the pressure–volume relationship for Xe(N₂)₂. The equimolar volume difference between Xe(N₂)₂ and Xe + 2N₂ gradually decreased with increasing pressure (up to 30 GPa). This result indicates that the tetragonal phase of Xe(N₂)₂ is likely unstable above 30 GPa, suggesting that Xe(N₂)₂ decomposes into Xe and N₂ or transforms into a denser phase. However, it is challenging to detect the phase transitions by XRD measurements at pressures up to 70 GPa, although small changes in the XRD profiles acquired at pressures greater than 30 GPa were detected. Thus, another experimental approach is necessary to identify the orbital interactions at high pressures. For example, highly sophisticated experiments such as high-temperature annealing or other spectroscopic methods could offer clear evidence for new Xe–N compounds, whether they involve chemical bonding between xenon and nitrogen or not.

Conclusions

By conducting room-temperature experiments on the Xe–N₂ system at pressures of up to 70 GPa, the van der Waals compound Xe(N₂)₂ was successfully synthesised. Xe(N₂)₂ forms a C15 Laves structure at pressures greater than 4.4 GPa. At approximately 10 GPa, the structure transformed into a tetragonal phase with a crystal structure like that of a high-pressure SiS₂ phase. This transition was reversible with pressure, and the volume difference was estimated to be 2.11%. At pressures greater than 45 GPa, the sample fluoresced, and the Raman peak frequencies with respect to the stretching vibrational mode of molecular nitrogen were either constant or shifted negatively with increasing pressure. This anomalous behaviour is likely due to the enhancement in the orbital interactions between xenon and nitrogen atoms at high pressure. Further high-pressure studies might lead to the successful synthesis of the theoretically predicted compound XeN₆.

The authors would like to thank Dr T. Kikegawa, Dr T. Nagae, and Prof. N. Watanabe for their technical support with the high-pressure, in situ synchrotron radiation XRD measurements. We also appreciate Dr Y. Shirako for the valuable discussions. Some experiments were carried out as part of a collaboration with the Institute for Solid State Physics, University of Tokyo. This research was supported by a Grant-in-Aid for Scientific Research from the Ministry of Education, Culture, Sports, Science, and Technology of Japan.

Notes and references

1. N. Bartlett, Proc. Chem. Soc., 1962, 112, 218.
2. L. Khriachtchev, M. Pttersson, N. Runeberg, J. Lundell and M. Räsänen, Nature, 2000, 406, 874.
3. D. R. MacKenzie, Science, 1963, 141, 1171.
4. M. Pettersson, L. Khriachtchev, A. Lingnell, M. Räsänen, Z. Bihary and R. B. Gerber, J. Chem. Phys., 2002, 116, 2508.
5. J. L. Weeks, M. Matheson and C. Chernick, J. Am. Chem. Soc., 1962, 84, 4612.
6. H. H. Claassen and J. G. Malm, J. Am. Chem. Soc., 1962, 84, 3593.
7. J. G. Malm, I. Sheft and C. L. Chernick, J. Am. Chem. Soc., 1963, 85, 110.
8. D. S. Brock and G. J. Schorobligen, J. Am. Chem. Soc., 2011, 133, 6265.
9. D. F. Smith, J. Am. Chem. Soc., 1963, 85, 816.
10. J. L. Huston, M. H. Studier and E. N. Sloth, Science, 1964, 143, 1161.
11. W. L. Vos, L. W. Finger, R. J. Hemley, J. Z. Hu, H. K. Mao and J. A. Schouten, Nature, 1992, 358, 46.
12. S. Ninet, G. Weck, P. Loubeyre and F. Datchi, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83, 134107.
13. T. Plisson, G. Weck and P. Loubeyre, Phys. Rev. Lett., 2014, 113, 025702.
14. G. Weck, A. Dewaele and P. Loubeyre, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 014112.
15. P. Loubeyre, R. Letoullec and J. P. Pinceaux, Phys. Rev. Lett., 1994, 72, 1360.
16. A. K. Kleppe, M. Amboage and A. P. Jephcoat, Sci. Rep., 2014, 4, 4989.
17. M. Somayazulu, P. Dera, A. F. Goncharov, S. A. Gramsch, P. Liermann, W. Yamg, Z. Liu, H. Mao and R. J. Hemley, Nat. Chem., 2010, 2, 50.
18. A. P. Jephcoat, M. Amboage and A. K. Kleppe, J. Phys.: Conf. Ser., 2010, 215, 012016.
19. A. Dewaele, N. Worth, C. J. Pickard, R. J. Needs, S. Pascarelli, O. Mathon, M. Mezouar and T. Irifune, Nat. Chem., 2016, 8, 784.
20. M. E. Kooi and J. A. Schouten, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 60, 12635.
21. F. Peng, Y. Wang, H. Wang, Y. Zhang and Y. Ma, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 92, 094104.
22. M. S. Anderson and C. A. Swenson, J. Phys. Chem. Solids, 1975, 36, 145.
23. A. N. Zisman, I. V. Aleksandrov and S. M. Stishov, Phys. Rev. B: Condens. Matter Mater. Phys., 1985, 32, 484.
24. H. Schneider, W. Hiifner, A. Wokaun and H. Olijnyk, J. Chem. Phys., 1992, 96, 8046.
25. C. T. Prewitt and H. S. Young, Science, 1965, 149, 535.
26. H. Olijnyk, J. Chem. Phys., 1990, 93, 8968.
27. V. E. Bondybey and J. W. Nibler, J. Chem. Phys., 1973, 58, 2125.
28. M. I. Eremets, A. G. Gavriliuk, I. A. Trojan, D. A. Dzivenko and R. Boehler, Nat. Mater., 2004, 3, 558.
29. D. M. Proserpio, R. Hoffmann and K. C. Janda, J. Am. Chem. Soc., 1991, 113, 7184.
30. J. M. Jean and K. B. Hall, Proc. Natl. Acad. Sci. U. S. A., 2001, 98, 37.

---

Footnote

† Electronic supplementary information (ESI) available: S1–S7, details of experimental set-up, Raman spectrum, XRD profiles and crystal structures. See DOI: 10.1039/c6cp06552j

---