Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Selective reduction of SWCNTs – concepts and insights†
Julian
Gebhardt
ab,
Sebastian
Bosch
bc,
Ferdinand
Hof
bc,
Frank
Hauke
bc,
Andreas
Hirsch
*bc and
Andreas
Görling
*ab
aChair of Theoretical Chemistry, Friedrich-Alexander-Universität Erlangen-Nürnberg (FAU), Egerlandstraße 3, 91058 Erlangen, Germany. E-mail: andreas.görling@fau.de
bInterdisciplinary Center for Molecular Materials (ICMM), Friedrich-Alexander-Universität Erlangen-Nürnberg (FAU), Henkestraße 42, 91054 Erlangen, Germany. E-mail: andreas.hirsch@fau.de
cChair of Organic Chemistry II & Institute of Advanced Materials and Processes (ZMP), Friedrich-Alexander-Universität Erlangen-Nürnberg (FAU), Henkestraße 42, 91054 Erlangen, Germany
First published on 23rd June 2015
Abstract
The charging of single-walled carbon nanotube (SWCNT) mixtures by reduction via alkali metal atoms is an established first step towards covalent SWCNT functionalization. In this combined density-functional theory and experimental study, we investigate this reduction with respect to differences occurring between tubes of different electronic type (metallic (m) and semiconducting (sc) tubes, respectively). We find that metals, specifically potassium, adsorb stronger to m- than sc-SWCNTs, which can be explained by the different band structures of both tube types. We investigate this trend in detail for a variety of different chiral SWCNTs, finding a potassium coverage dependent preference of m- over sc-SWCNTs, which is predicted to allow for a selective charging of metallic tubes for K/C ratios ≤ 1/200. This selective charging can be translated into the enrichment of m-SWCNTs during dispersion of SWCNT mixtures, since only reduced tubes are dissolved from the bulk material. The results for isolated tubes can be generalized to SWCNT bundle arrangements, which means that the theoretical predicted selective charging is transferable also to this more realistic description of the experimental systems. The theoretical findings regarding an electronic type selective charging of SWCNTs have been verified by an experimental study. By a combination of Raman and absorption/emission spectroscopic analysis, a preferential dispersion of charged metallic carbon nanotubes in THF as solvent was found for the predicted low potassium concentrations. Our results lead to the conclusion that previous m/sc selective reductive functionalization reactions cannot be explained on the basis of an electronic type selective charging step, as these reactions used much higher alkali metal concentrations.
1 Introduction
Single-walled carbon nanotubes (SWCNT) are usually synthesized via arc discharge, laser ablation or chemical vapor deposition (CVD) techniques.1 The resulting product is a vast mixture of tubes with different structural properties such as length, diameter, electronic type (semiconducting (sc) or metallic (m)), and helicity. The separation of such mixtures to obtain monodisperse tubes in a routine and cost-efficient way remains an unsolved problem of great importance in SWCNT science, i.e., in the fields of its chemistry, characterization, and envisioned applications.Over the past years, a variety of different approaches evolved that try to gain access to a specific type of SWCNT.2,3 By controlling the synthesis parameters, the diameter of the grown SWCNT can be controlled to some extent. However, since the relation between chiral vector and tube diameter is not unambiguous, especially for larger diameters, pure monodisperse synthesis is not achievable with such methods, which, in addition, lack upscaling potential and cost efficiency.
Therefore, many research efforts were directed towards the sorting of commercially accessible SWNCT mixtures post synthesis. Here, many different methods exist that are more or less harsh or destructive.4–6 One possibility is selective destruction, which is powerful for some applications, but does not provide monodisperse SWCNTs. In contrast, a non-covalent7 or covalent8 chemical sorting of SWCNT mixtures provides a promising approach for a bulk separation of metallic and semiconducting systems and is, therefore, among the variety of methods, thought to be the most promising candidate for producing monodisperse SWCNTs.2 A meanwhile routinely applied protocol9 for the covalent functionalization of SWCNT mixtures involves the reduction of SWCNTs by alkali metals, e.g., by a Birch type reaction, in which the negatively charged intermediates, also called carbon nanotubides, are functionalized, involving electrophiles and single-electron transfer processes. The respective reduced carbon nanotubes are promising starting materials, yielding functionalized SWCNTs with a broad variety of different functional groups.10–14
We have shown, that the same carbon nanotubide starting material, generated under Birch type conditions with lithium as reducing agent, leads to a preferential functionalization of metallic or semiconducting tubes, respectively. Depending on the nature of the trapping electrophile, the reaction shows preference for metallic (diazonium salts) or semiconducting tubes (carbon dioxide).15 This observation directly leads to the question which parameters are responsible for a type selective functionalization of carbon nanotubes in the course of a reductive alkylation/arylation scenario.
Herein, we investigate the possibility of a selective SWCNT separation on the basis of the initial charging step by a combined theoretical and experimental study. More precisely, can the reduction of the SWCNT mixture itself be responsible for their electronic type selective separation/functionalization?
We have shown recently that the initial SWCNT charging can be carried out in a clean and efficient way by a solid state intercalation of SWCNTs by potassium.16 The alkali metal concentration can be varied and has a direct influence on the final degree of functionalization.
In the present work, we study the influence of potassium – and other alkali and earth alkali metals – on a broad set of chiral sc- and m-SWCNTs, as well as on bundles of semiconducting, metallic, and mixtures of sc- and m-tubes by density-functional theory (DFT) calculations. We find that the SWCNT charging process by metals is concentration dependent, and that it shows selectivity with respect to the electronic type, favoring metallic over semiconducting tubes for small alkali metal concentrations (see Fig. 1). We validate our theoretical predictions by experiments, showing an approach towards a post synthesis chemical sorting of SWCNT mixtures via covalent functionalization. In summary, our findings show that a preferential reduction of metallic SWCNT species is obtained for low potassium to carbon ratios of K/C < 1/200.
 | ||
| Fig. 1 Selective charging and subsequent dispersion of SWCNT mixtures, showing a preference of metallic (orange) over semiconducting (blue) tubes at the given experimental conditions. | ||
By tailoring the experimental parameters, according to the results obtained from our DFT calculations, we are now able to obtain selectively enriched metallic SWCNTs. This low reducing metal concentrations have hitherto not been used in reductive functionalization reactions and may be further exploited in an electronic type selective sorting of SWCNT mixtures.
2 Computational and experimental details
DFT calculations
The periodic DFT calculations were carried out with the Vienna-ab initio-Simulation Package,17 employing a plane-wave basis set and the projector-augmented-wave method18 for the treatment of core electrons. Exchange and correlation were treated within the generalized-gradient approximation (GGA) by the Perdew–Burke–Ernzerhof (PBE) functional.19 An energy cutoff of 415 eV was used together with a first order Methfessel–Paxton level broadening20 of 0.15 eV. Energies were converged to 10−6 eV and forces acting on atoms to 10−2 eV Å−1. For the computations of isolated tubes, a single SWCNT was placed along the z direction in a rectangular box using periodic boundary conditions. Using periodic boundary conditions, and, therefore, formally infinitely long systems as models for long but finite SWCNTs, is justified as long as one is not interested in the specific effects of the tube termination. The starting geometries of the tubes were generated with the TubeGen 3.4 web interface.21 Vacuum along the x- and y-directions ensures a tube–tube separation of 15 Å. The Brillouin zone was sampled using a Monkhorst–Pack k-point grid22 of 1 × 1 × 9 k points. As reference for the metal binding energies, we chose the metal bulk energies per metal atom as calculated by our DFT setup. With these metal reference values (EM) and the energies of the isolated SWCNTs (ECNT), adsorption energies (Eads) per metal atom (n) are defined as| Eads = (ECNT+nM − ECNT − nEM)/n, | (1) |
We chose this metal reference since crystalline metal is melted together with the nanotube mixtures in experiments.16 Other choices for the reference would only shift all adsorption energies but would not influence the obtained trends. A different reference is provided, e.g., by isolated metal atoms. However, the chosen bulk reference leads to adsorption energies that can be considered as lower limit, while adsorption energies with respect to energies of isolated metal atoms would serve as upper limit (the difference per atom in the case of potassium is 0.87 eV).
Band structures and densities of states (DoS) were computed with an increased k-point grid of 81 k points along Γ–X and a Gaussian broadening with 0.025 eV width. Charge-density differences (CDD) were calculated analogously to ref. 23. For the calculation of SWCNT bundles, a semiempirical van der Waals correction24 was added to take dispersive interactions between the tubes into account. The effect of this correction on the adsorption energy of a single potassium atom on an isolated tube is a constant shift of 0.03 eV, i.e., the van der Waals contribution of the metal-tube bond is negligible.
Materials
Purified HiPco SWCNTs (grade: pure; lot number P0261, TGA residue 13.3 wt) were used without further treatment. THF was distilled three times in an argon inert gas atmosphere over (i) CaH 2, (ii) sodium, and (iii) sodium–potassium alloy. The remaining traces of oxygen were removed by a pump freeze technique (3 iterative steps).SWCNT charging and dispersion
For the preparation of carbon nanotubides with varying K/C ratios (1/50, 1/100, and 1/250), HiPco SWCNTs and the respective amount of potassium were heated at 150 °C for 12 hours in an argon filled glove box (<0.1 ppm oxygen; 0.1 ppm H2O). Afterwards, the black salts were cooled to room temperature. For their subsequent dispersion, 5 mL of THF were added to 5 mg of the respective samples, followed by a short ultrasonication treatment with a tip sonicator (Bandelin UW 3200; 5 min, 100 J). The setup was left 24 hours for sedimentation. Afterwards, the supernatants were separated and used for absorption and fluorescence spectroscopy. For Raman measurements under inert gas conditions the supernatants were filtered through a 0.2 μm reinforced cellulose membrane filter (Sartorius) and washed with THF under argon. The corresponding SWCNT paper was placed between two glass slides and was airtightly sealed with parafilm. For further experimental details see ESI.†3 Results and discussion
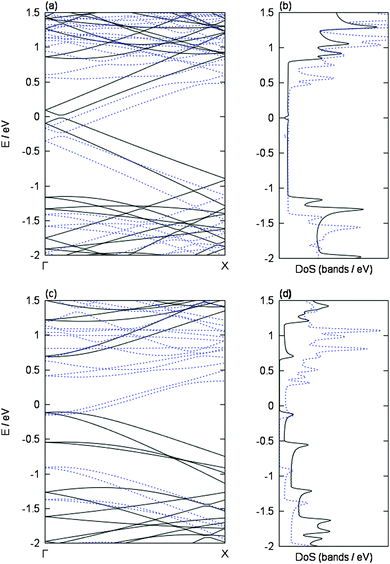
In the first part of our study we investigated the selective charging of carbon nanotubes due to their electronic type on the basis of a detailed DFT inspection of the respective metal/SWCNT interactions. Therefore, we consider exemplary two isolated chiral SWCNTs in vacuum of comparable diameter size (≈8.3 Å), namely the semiconducting (8,4) and the metallic (9,3) tube. We have chosen these two tubes as they are representative examples for chemical reactive SWCNTs at the lower diameter regime of our experimental HiPco sample. Furthermore, for our initial calculations, we wanted to avoid diameter based influences.The band structure and DoS of both tubes are shown in Fig. 2. The obtained results are similar to what is predicted from tight-binding models [1] within the zone-folding approximation. The semiconducting (8,4) tube has a band gap of 0.80 eV with zero DoS around the Fermi level. Note that GGA functionals, like the PBE functional employed here, are able to correctly predict trends of band gaps but are known to systematically underestimate them. The metallic (9,3) tube has a Dirac cone, i.e., no band gap but finite DoS in the vicinity of the Fermi level.
More precisely, due to the effects of the geometric curvature of the tube,25–27 the Dirac cone is shifted away from its position predicted from the zone-folding approximation and a small band gap of 0.04 eV is obtained in the more realistic DFT description, which is in line with experimental results28 and earlier theoretical studies.29–31 The van Hove singularities (see, e.g., ref. 27) of the DoS are well resolved in both cases (Fig. 2(b) and (d)).
Next, potassium atoms are added to both SWCNTs. We tested different possible adsorption geometries, namely adsorption on top of carbon atoms of both hexagon sublattices (A and B), adsorption over a carbon–carbon bond, and adsorption over the center of a carbon hexagon. We find that adsorption over the center of a carbon hexagon (see Fig. S7, ESI†) is the only stable adsorption site for both tubes, which is in line with structures assumed in earlier studies32–35 and with adsorption positions found for potassium adsorbed on graphene/graphite.36,37 In this optimal geometry, the potassium atom has six carbon neighbors with almost identical adsorption distances of ≈3.0 Å. The adsorption energies per potassium atom for the sc-(8,4) and the m-(9,3) tube are −0.25 and −0.56 eV, respectively.
We compared this most stable exohedral adsorption with endohedral adsorption inside the tube. The resulting optimal structure is similar to the obtained exohedral structure (see Fig. S7 for details, ESI†) but turns out to be energetically more stable, which is in line with previous studies.38
However, the situation of isolated tubes in vacuum is not a realistic model of the experimental situation, where tubes are present in bundles, closely connected to each other by van der Waals forces. In such bundles, the exohedral adsorption will be favored due to the possible interaction of every potassium atom with several tubes (see ESI† and below).38–40 Therefore, we concentrate on exohedral adsorption in our discussion.
The different adsorption energies of a potassium atom in the stable exo-adsorption structure on the (8,4) and the (9,3) tubes indicates a stronger binding of potassium atoms to metallic tubes. This, however, indicates the possibility to selectively reduce preferentially metallic tubes in SWCNT mixtures and, consequently, to separate metallic from semiconducting tubes during the dispersion step that follows the charging of the bulk material (see Fig. 1).
To analyze this in detail, the influence of a single potassium atom on the band structures and the DoS of our two exemplary tubes is shown in Fig. 2. In both cases, the Fermi level is shifted upwards upon adsorption of potassium, i.e., bands that are located above the Fermi level in the pristine cases become occupied due to the adsorption of potassium. This is in line with the donation of the potassium valence electron to the respective tube bands, i.e., n-doping (or reduction) of the tubes, in agreement with earlier studies.38,40,41 This is also confirmed by a Bader analysis,42 according to which 0.90–0.91 electrons are transferred from the potassium atom to the respective carbon nanotube. This is in line with Mulliken charges obtained in earlier studies of metals adsorbed on SWCNTs.43 The raising of the Fermi level is more pronounced in the semiconducting tube due to its band gap. Besides the shifting of the Fermi level, the band dispersion remains almost unchanged, i.e., no noticeable hybridization between carbon and potassium bands is observed.
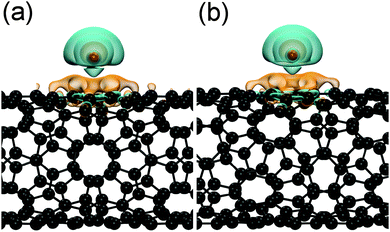
The additional charge of the reduced tubes is rather localized, as it is shown by the charge-density difference plots in Fig. 3. In both cases, i.e., for the sc-(8,4) and the m-(9,3) SWCNT, charge is depleted around the potassium atom, which is mostly accumulated at the carbon atoms of the hexagon below the adsorbed potassium atom.
Next, we tested the possibility to reach a better reduction preference of metallic over semiconducting tubes by exchanging the metal atom. For this purpose we screened the effect of different metal atoms including M = Li, Na, K, Mg, Ca, Sn, Zn, and Hg. The selective reduction of sc/m-SWCNT mixtures will depend on the difference in adsorption energies of metallic and semiconducting tubes. Therefore, we compared the adsorption strength of the selected metals on the two tested tubes. The data collected in Table 1 shows that potassium is already the most promising candidate.
| Li | Na | K | Mg | Ca | Zn | Hg | Sn | |
|---|---|---|---|---|---|---|---|---|
| E ads(8,4) | 0.40 | 0.41 | −0.25 | 1.49 | 1.41 | 1.08 | 0.14 | 2.79 |
| E ads(9,3) | 0.13 | 0.11 | −0.56 | 1.48 | 1.18 | 1.08 | 0.14 | 2.68 |
On the one hand, potassium is the only tested metal that exhibits a negative binding energy. However, binding energies are dependent on the chosen metal reference (see Computational details). Moreover, more negative binding energies are obtained in the more realistic case of bundles of SWCNTs. Therefore, the difference of the adsorption energies of sc- and m-tubes is more important, which is maximal in the case of potassium with an adsorption energy difference of −0.31 eV. In summary, potassium seems to be already the perfect candidate for the selective reduction of carbon nanotubes by metal atoms, although other metals show a comparable separation potential with adsorption energy differences between −0.23 and −0.30 eV (Ca, Li, and Na).
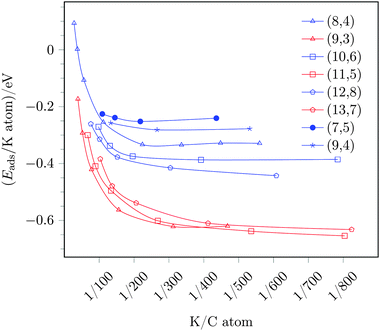
As a next step, we investigated the coverage dependence of the adsorption energy, i.e., we compared the adsorption energies per potassium atom with increasing coverage, see Fig. 4. Fig. 4 shows a decreasing adsorption energy for both, the sc-(8,4) as well as the m-(9,3) tube, with increasing potassium coverage, i.e., for larger potassium to carbon atom ratios. In the region of K/C ratios of 1/200 and above, the difference of the adsorption energies of (8,4) and (9,3) tubes decreases, and the selectivity of the reduction of tubes becomes less distinct. This means that for K/C ratios larger than 1/100, the adsorption energy per potassium atom on the metallic (9,3) SWCNT becomes less negative than the adsorption energy on the semiconducting (8,4) SWCNT at a smaller K/C ratio of 1/200 and below.
In the low coverage regime, i.e., for coverages corresponding to K/C ratios of 1/200 and below, the potassium adsorption energies remain almost constant and, thus, a constant, maximal preference of reducing metallic over semiconducting tubes is observed with an adsorption energy difference of −0.29 eV. Assuming a Boltzmann distribution, this equals ratios of reduced (9,3)/(8,4) tubes of ≈104–102 for temperatures ranging from 300 to 600 K. Thus, a considerable separation should be achievable in theory.
In order to investigate whether or not this result is transferable to a broad mixture of different tubes, we investigated a series of different metallic and semiconducting tubes with different diameter, in addition to the (8,4) and (9,3) tubes considered thus far. We chose the metallic (11,5) and (13,7) SWCNTs and the semiconducting (10,6), (12,8), (7,5), and (9,4) tubes. This choice is motivated by several reasons: on the one hand the pairs (11,5)–(10,6) and (13,7)–(12,8) have comparable diameter of 11.0 and 13.7 Å, respectively. As a result, the three studied m/sc-pairs of comparable diameter ((9,3)–(8,4), (11,5)–(10,6), and (13,7)–(12,8)) cover, with a diameter range of ≈8.3–13.7 Å, the range of the majority of tube diameters that are found in the tube mixtures that were used in our experiments (see Experimental details and below). On the other hand, the (7,5) and the (9,4) sc-tubes are two tubes with large abundance in the used experimental probes and are, therefore, used to analyze the experimental results in detail, as their excitations are probed by the applied laser wave-length in our Raman measurements (see below).
The adsorption energies of potassium with varying coverage on these tubes are also included in Fig. 4. From this data one can deduce the following trends:
(i) For low coverages and K/C ratios of ≤1/200, adsorption on metallic tubes is always preferred over adsorption on semiconducting tubes, independent of the tube diameter.
(ii) In the case of metallic tubes, only a small influence on the tube diameter is observed, and beyond the threshold of K/C ≈ 1/200, the adsorption energies are almost identical for all three probed metallic tubes. This trend can be understood by the band structure of metallic tubes. Since the band structure of all metallic tubes contain Dirac cones, the lowest unoccupied states are almost identical for all metallic tubes and, consequently, so is the electron affinity and the potassium adsorption energy.
(iii) In contrast, the semiconducting tubes show a strong diameter dependency, namely an increased adsorption energy with the diameter size. This is, once again, in line with the band structure of the tubes. The band gap of semiconducting tubes decreases with the diameter size. In the limit of an infinite diameter the band structure would, therefore, converge to the graphene band structure, i.e., to zero band gap.27 In our tested cases the band gap decreases with increasing diameter from 0.80 to 0.52 eV from the (8,4) to the (12,8) tube, respectively. A decreased band gap, however, is tantamount with the lowest unoccupied states located at smaller binding energies, i.e., located closer to the Fermi level. This results in an easier reduction of the tube and, thus, a larger potassium adsorption energy for large sc-tubes with small band gaps compared to smaller sc-tubes with larger band gaps. Note, however, that this trend only applies for large diameters and that this trend, explained by the zone-folding approximation, breaks down for small diameters due to curvature effects, i.e., the fact that a SWCNT does not have a planar electron system but, as a tube, obviously exhibits a curvature that, however, is not taken into account in the zone-folding model.44 This is also evident for the band gaps and, thus, potassium adsorption energies obtained for two different investigated sc-chiral tubes [(7,5) and (9,4), respectively, see Fig. 4], the results of which do not follow simply the trend of the diameter change compared to the sc-(8,4) tube.
In summary, the adsorption energy differences of potassium on different SWCNTs are dominated by the electronic structure of the tubes rather than other effects like the expected increased reactivity with decreasing diameters due to the increasing curvature, which would, in fact, result in opposite trends.
Due to this different behavior of metallic and semiconducting tubes, the adsorption energy difference varies, depending on the diameter of the semiconducting SWCNT. In the region of maximal separation, i.e., K/C ratios of ≤1/200, the preference of metallic tubes is given by 0.2–0.3 eV, depending on the band gap (diameter) of the sc-tube. In any case, reduction of sc/m-SWCNT mixtures by low potassium coverages will always be favorable on metallic over semiconducting tubes.
The fact that this preference occurs only at low coverages is probably the reason why such an electronic type selective enrichment was not observed in previous experiments. This is, because reduction of SWCNTs by alkali metals was usually studied for much larger M/C ratios of 8/1–16/1,16,45 and, especially experimentally, often large amounts of reduction agents were used.46
The reasons for the usage of larger amounts of reduction agents are of practical nature: solvation of SWCNTs is difficult and is increased with the total charge transferred onto each tube.16,47–50 Therefore, working at lower coverages is counter intuitive regarding efficiency. Indeed, commercially available SWCNT mixtures are yet quite costly and the experimental realization of low potassium coverages in small SWCNT probes has natural limitations. Therefore, in order to realize small potassium concentrations, one usually works with increased amounts of SWCNTs, i.e., performs more costly experiments.
Before we discuss our experimental results, obtained for small potassium coverages as suggested by our computational results, we want to address one additional aspect theoretically. Until now, we considered a variety of different tubes that should be representative for the mixtures used in experiments. However, all calculations thus far considered isolated tubes. Experimentally, the tubes are present as bundles of various different tubes, interacting strongly via van der Waals interactions. Therefore, the question arises how such a more realistic arrangement alters the previously discussed results.
To that end, we studied a variety of different arrangements as models for the experimentally present SWCNT bundles, using as examples our main test systems, i.e., the semiconducting (8,4) and the metallic (9,3) SWCNT. In order to describe the van der Waals interactions in such structures properly, we included a dispersion correction to our GGA functional (see Computational details). While dispersive interactions play a major role in the description of tube–tube interactions within bundles, the adsorption of potassium atoms to the tubes has only little van der Waals contribution. The adsorption energy of one potassium atom on isolated (8,4) and (9,3) tubes changes by a negligible constant shift of 0.04 eV. This means, the trends of Fig. 4 are not at all affected by additional dispersive interactions.
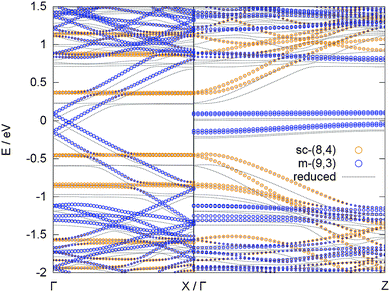
The most important question to answer is what happens to the adsorption preference of a potassium atom in a combined system of metallic and semiconducting tubes. Such a combined system of different tubes is not easily realized due to the different periodicity of each tube. We realized such a model by placing two different tubes into a rectangular unit cell on top of each other, with one SWCNT [(9,3)] oriented in x and the other [(8,4)] in z direction, see Fig. 5. The band structure of such a combined system is displayed in Fig. 6, together with the effect of a potassium atom added to the system.
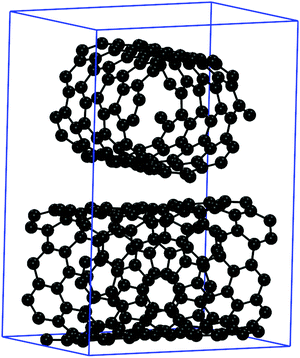 | ||
| Fig. 5 Combined system of sc-(8,4) (top) and m-(9,3) SWCNT (bottom) in a rectangular unit cell (blue box). Carbon atoms are represented by black spheres. | ||
The bands of the two tubes align in such a way that the Fermi level of the combined system is located in the middle of the band gap of the semiconducting tube. Consequently, the lowest unoccupied states, which become occupied due to the valence electron of the potassium atom in the reduced case, belong to the π* band of the metallic tube, i.e., the metallic tube is reduced, in line with the results deduced from the isolated tubes. This is also in line with a Bader analysis, which attributes 89% of the 0.9 electrons that are transferred from the potassium atom to the SWCNTs to the metallic (9,3) tube and only 11% to the semiconducting (8,4) tube.
In addition to the above system combining two different SWCNTs, we investigate the influence of bundles containing one type of SWCNT. Two different structures were investigated, namely a rectangular arrangement of two parallel tubes on top of each other and a hexagonal-closed packed (hcp) structure of each tube (see Fig. S8, ESI†).
In the rectangular arrangement, the potassium adsorption energy is increased compared to the isolated tubes by 0.16 and 0.48 eV for (8,4) and (9,3) SWCNT, respectively. This corresponds to an increased adsorption energy difference between the sc-(8,4) and the m-(9,3) tube of 0.63 eV, i.e., a doubling of this difference compared to the isolated tubes (adsorption energy difference of 0.31 eV). This means that the separation of metallic and semiconducting tubes should be even increased compared to the arrangements of isolated tubes. However, in the case of the hcp arrangement, both adsorption energies are decreased by 0.18 and 0.24 eV for (8,4) and (9,3) SWCNT, respectively. This is due to the stronger tube–tube interactions in this arrangement. Tube–tube interactions arise in all bundle models and are a concurring force to the adsorption of potassium. In the pristine (not reduced) rectangular arrangements, they result in tube–tube binding energies of 2.04 and 2.56 eV per unit cell of the (8,4) and the (9,3) tube, respectively. In the hcp structures, however, these binding energies are considerably increased to 2.98 and 4.38 eV per (8,4) and (9,3) tube, respectively. This means, upon maximizing the tube–tube binding energy, the adsorption energy of the potassium atom is reduced overall in the case of the hcp structures. The changed potassium adsorption energies result in a slightly decreased potassium adsorption energy difference compared to the isolated tubes between (8,4) and (9,3) tubes of 0.25 eV (decrease of 0.06 eV). In summary, we want to stress that the description of realistic SWCNT bundles is quite challenging and beyond the scope of this work. For instance, the solution/dispersion of the reduced SWCNTs, i.e., the influence of solvent on the mixture of reduced/pristine SWCNT bundles, is yet to be investigated. Our studied model cases demonstrate a considerable influence on the arrangement, nevertheless, in all tested cases the adsorption energy difference between semiconducting (8,4) and metallic (9,3) SWCNT is preserved and we are, therefore, confident that this is also the case in the experimental mixtures. In experiments, structures that are less ordered than the considered hcp bundle can be assumed. Thus, the hcp arrangement should represent the lower boundary of metallic/semiconducting separation potential.
In addition, our model systems show that interaction with multiple tubes stabilize exohedral adsorption (in bundles of parallel SWCNTs with tube axes forming a rectangular arrangement, see Table S2 for details, ESI†). In a hexagonal closed-packed (hcp) arrangement of a specific SWCNT, here (8,4) or (9,3) tubes, respectively, such a stabilization of exohedral adsorption is not observed. This can be attributed to the maximized tube–tube interactions in such a highly ordered structure of a specific SWCNT. Such a close-packed structure, however, is unrealistic for mixtures of SWCNTs that are considered here. Therefore, potassium atoms are likely to be adsorbed exohedral between several tubes in bundles of mixed SWCNTs.
From the experimental side, the investigation of a selective charging of metallic SWCNTs at very low potassium concentrations (K/C < 1/200) is a highly challenging task, as the metal concentration has to be varied and controlled in a precise and reproducible manner. We generated the respective carbon nanotubides according to our recently published solid-state reduction protocol.13,14,16 The advantage of this sequence over alternative nanotubide generating procedures is the absence of further co-reducing agents such as liquid ammonia or naphthalene,49,51,52 which would severely interfere the comparison of the experimental data with the theoretical predictions. In addition, it is important to mention that a successful preparation of carbon nanotubide salts exhibiting a very low amount of potassium requires absolute oxygen and moisture free conditions, which demands working in argon filled glove box atmosphere with less than 0.1 ppm oxygen and water, respectively.16 In order to verify the theoretical prediction that at potassium to carbon ratios of about 1/200 an electronic type selective charging of m-SWCNTs can be expected, whereas below this threshold only a minor selectivity should be observed, we prepared three nanotubide samples with K/C ratios of 1/50, 1/100, and 1/250. Note that the theoretical predicted threshold of a K/C ratio of 1/200 would translate into a significant lower experimental K/C ratio, keeping in mind that we computed pure metallic or semiconducting tubes, whereas in the experimental HiPco starting material, a mixture of m/sc-tubes of roughly 1/4 is measured (see, e.g., Fig. 7). Unfortunately, we could not generate samples containing potassium coverages below 1/250 in a reproducible manner, due to experimental limitations. Nevertheless, our experiments with a K/C ratio of 1/250 are located at the lower boundary where a selective charging should still be observable, which is indeed the case, as we will show in the following.
In order to develop separation protocols based on a selective charging of m-SWCNTs, the respective carbon nanotubide salts have to be dispersed in an appropriate solvent, which has to be inert under the respective experimental conditions and absolute free of oxygen and water. As we have shown recently, three times distilled and subsequently three times pump-freezed THF is a suitable solvent that fulfills both demands.16 The nanotubide salts with varying potassium coverages were prepared inside a glove box under strict inert gas conditions. For an efficient dispersion of the negatively charged SWCNTs, the respective potassium salt was sonicated (100 J, no pulse sequence) in THF for 5 minutes. After one day of sedimentation, the supernatants were separated and the different samples were studied by a combination of UV-vis/nIR and fluorescence spectroscopy as well as scanning Raman spectroscopy (SRS). SRS is the most suitable analytical technique for extracting bulk information of the respective SWCNT samples.15 Therefore, large areas of 50 × 50 μm2 were sampled by recording 2500 spectra and the resulting data was statistically processed.
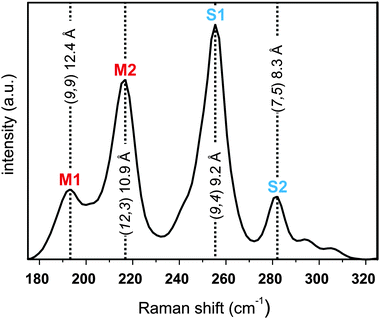
A typical Raman spectrum of the studied SWCNTs comprises several characteristic peaks, such as the radial breathing modes (RBM), the defect induced D-mode and the graphitic mode (G-mode).53 In carbon allotrope Raman analysis, the intensity ratio of the D-mode compared to the G-mode can be used as a measure for the amount of covalently bound addends in functionalized samples.15,54 The RBM modes are a unique feature for SWCNTs and their respective position is depending only on their diameter and the applied laser excitation energy.55 Our sample excitation has been carried out with an excitation wavelength of λexc = 633 nm. This distinct wavelength ensures that both electronic types – semiconducting and metallic nanotubes – are recorded in the respective SRS measurements. Here, differences in the RBM intensities can provide valuable information about underlying variations in the composition of the separated samples. In the pristine starting material (Fig. 7) four prominent peaks are observed in the RBM region, which can be assigned in agreement to literature.55,56 Peaks at 196.3 and 220.9 cm−1 are attributed to the two metallic tubes M1 (9,9) and M2 (12,3) with diameters of 12.4 and 10.7 Å, respectively, and the two peaks at 256.0 and 288.4 cm−1 can be assigned to the two semiconducting carbon nanotubes S1 (9,4) and S2 (7,5) with diameters of 9.2 and 8.3 Å, respectively.
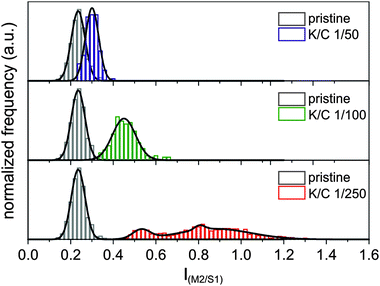
Consequently, we measured the intensities of the two most prominent semiconducting and metallic RBM peaks M2 and S1 with respect to the G-mode and used this as a measure for the enrichment of metallic or semiconducting species in our sample. Analogously to our previous statistical data processing,15 we plotted the frequency of the intensity ratios as histograms and determined their distribution functions. For the pristine starting material, we find a Gaussian distribution centered at an intensity ratio of 0.24 IM2/S1 and a standard deviation of σ = 0.065 (see Fig. 8). This is in line with the known larger abundance of semiconducting versus metallic tubes in our commercially available starting material, with a ratio of m/sc-tubes of about 1/4.
By a comparison of the RBM intensity ratio in the pristine SWCNT material (gray histogram in Fig. 8) with the data obtained for the reductively charged and dispersed nanotubides – K/C ratio of 1/50 (blue histogram in Fig. 8), only a negligible shift of the Gaussian distribution towards an intensity ratio of 0.30 IM2/S1 is observed, with an almost unchanged statistical deviation of σ = 0.062. By decreasing the potassium coverage to a K/C ratio of 1/100 (green histogram in Fig. 8), the intensity ratio is slightly shifted to 0.45 IM2/S1, whereas the standard deviation of the distribution is increased by a factor of roughly two (σ = 0.109). This leads to the conclusion that the distribution between semiconducting and metallic species in this nanotubide sample resembles more or less the same ratio as detected for the starting material. Nevertheless, a small trend towards an electronic type selective charging of metallic tubes can be seen in the respective IM2/S1 plot.
This situation drastically changes when a lower potassium concentration is used for the initial charging – K/C ratio of 1/250 (red histogram in Fig. 8). Here, the center of the distribution of the measured SRS data shifts to an intensity ratio of 0.83 IM2/S1. In addition, the distribution is severely broadened, with a standard deviation of σ = 0.272. This means that the sample contains enriched metallic SWCNTs with a m/sc ratio of up to 1.2. This corresponds to an enrichment factor of about 20% to 55%, whereas the statistical mean value of 0.83 IM2/S1 still corresponds to an enrichment of 45%. Keeping in mind that our minimal experimental potassium coverage is at the lower boundary side of the predicted separation potential, the observed selective enrichment of metallic tubes is a very promising result.
This trend towards an electronic type selective charging of metallic tubes followed by their preferential dispersion in THF is also traceable if other RBM peak ratios are considered for data analysis, i.e., M1/S1, M1/S2, and M2/S2 (see Fig. S1 in the ESI†). However, since the M1 and S2 intensities are weaker at the chosen excitation energy, the resulting trend is less pronounced in the respective histograms.
In addition to the discussed RBM peaks, histograms of the intensities of G′- and G-modes (see Fig. S2 in the ESI†) can be used for the analysis of the charge driven enrichment of metallic SWCNTs and the obtained results are fully in line with the conclusions drawn from the RBM distributions.
The detected changes of the peak intensities of the RBM modes as well as the G′-mode are unique for the charged separated samples and cannot be traced back to covalent sidewall functionalization as the peak intensity ratio of the D/G value was practically not altered in the course of the separation process (Fig. 9). The respective median spectra of all samples are presented in Fig. S3 (ESI†).
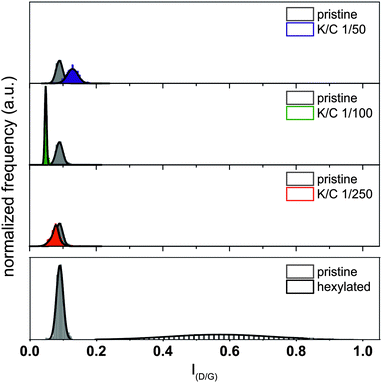 | ||
| Fig. 9 Analysis of the introduction of defects (i.e., covalent functionalization) based on the ID/G ratio. Pristine starting material (grey); K/C ratios: 1/50 (blue), 1/100 (green), and 1/250 (red). For comparison: histogram of a representative sample, functionalized via reductive alkylation, data taken from ref. 16. | ||
In addition to the supernatant, we have also determined the IM2/S1 ratios in the precipitated fraction of our samples and found no significant changes in the composition (see Fig. S4, ESI†). This can be explained by the respective low amount of dispersed carbon nanotubides in the supernatant leaving the precipitate composition almost unchanged.
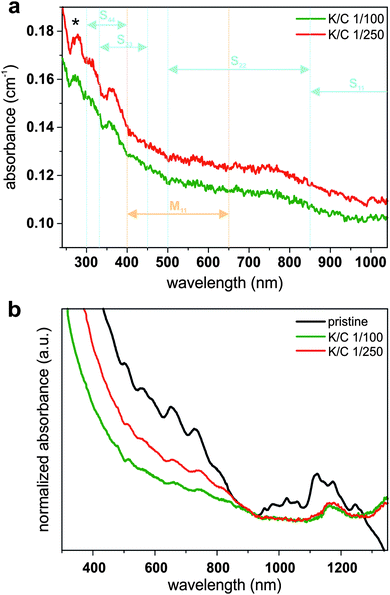
In contrast to the charged carbon nanotubes, the pristine material cannot be dispersed in THF in a stable fashion, especially not with a short sonication time of 5 minutes (Fig. S5, ESI†). This means, only the charged fraction of our SWCNT mixtures is dispersed and can, therefore, be studied with optical spectroscopy (Fig. 10). Unfortunately, we only found transitions in the S33 region (between 325 and 450 nm) for all of our reduced samples (K/C of 1/50–1/250). This observation suggests the filling of the lower lying conduction bands upon reduction (even for very low doping levels). It has to be mentioned that the experimental findings cannot be directly related to our calculations, where – when the primary charging by potassium atoms is considered – transitions in the S22 regions should be detectable, even at high potassium concentrations, but dependent on the number of atoms per unit cell and, therefore, the specific nature of the respective nanotube. However, it should be kept in mind that under experimental conditions bundling effects, the interaction of the charged nanotubides with the solvent, and the solvation of the counter ions have a fundamental impact on the recorded absorption spectra.
However, by leaving the sample for one week under ambient conditions, we observe a reappearing of all excitonic transitions due to an oxidation of the negatively charged carbon nanotubides, in agreement to our previous studies.16 This oxidation step is inevitably connected with a covalent modification, which is manifested in an attenuation of some excitonic transitions (Fig. 10a).12 Nevertheless, excitonic transitions that have been quenched in the charged state, become detectable in the reoxidized samples (Fig. 10b). This effect is more pronounced for transitions in the metallic M11 region (between 400 and 650 nm) than for transitions in the S22 region (500–850 nm). S11 absorption bands (850–1300 nm) do not reappear due to covalent modifications during reoxidation. Furthermore, the π-plasmon band intensity at 280 nm (i.e., the collective excitation of the π-electron system polarized along the nanotube axis) is more pronounced in the case of the K/C 1/250 sample, which is also an indication for a metallic chirality enriched sample mixture.57 These findings indicate that the composition of the charged material in the supernatants after reduction with potassium indeed is enriched in metallic species, corroborating the theoretical predictions and our Raman analysis (Fig. 8). Moreover, the data is also in line with the spectral information extracted from the fluorescence spectroscopic investigation of the redispersed samples (Fig. S6, ESI†).
In contrast to the charged samples, which exhibit a complete quenching of the intrinsic fluorescence, the redispersed samples still exhibit emission intensity of semiconducting SWCNTs. However, compared to the pristine starting material, the emission of the redispersed nanotubes is significantly decreased in its intensity as the sample composition after reduction is enriched in metallic species by the dispersion/extraction process of selectively charged SWCNTs.
4 Conclusions
In summary, our experimental data are consistent with the theoretical prediction that charging of the carbon nanotube mixtures is selective for metallic tubes for small potassium ratios of K/C ≤ 1/200. The selective charging is less pronounced for higher potassium coverages, i.e., in our samples with K/C 1/50 and 1/100. In principle, this selective reduction can be exploited in charge separation protocols, in order to enrich samples with metallic SWCNTs. For a better separation, however, experimental shortcomings need to be overcome, as very low K/C ratios have to be reached reproducibly, in order to fully exploit the separation potential of the selective charging step.On the basis of our results, electronic type selectivity observed in previous studies of covalent SWCNT reactions cannot simply be referred to a selective charging of the specific helicities in the starting mixture, as potassium concentrations much higher than the critical threshold calculated here have been used. Consequently, in order to understand the underlying principle of electronic type selective SWCNT reactions, the focus of further studies should be turned towards the specific interactions of the charged carbon nanotubides and the final trapping reagent as well as on the respective electron transfer kinetics.
Acknowledgements
The authors thank the Deutsche Forschungsgemeinschaft (DFG-SFB 953, Projects C2 and A1 “Synthetic Carbon Allotropes”), the Interdisciplinary Center for Molecular Materials (ICMM), and the Graduate School Molecular Science (GSMS) for financial support.References
- R. Saito, M. S. Dresselhaus and G. Dresselhaus, Physical Properties of Carbon Nanotubes, Imperial College Press, London, 1998 Search PubMed.
- M. C. Hersam, Nat. Nanotechnol., 2008, 3, 387–394 CrossRef CAS PubMed.
- H. Zhang, B. Wu, W. Hu and Y. Liu, Chem. Soc. Rev., 2011, 40, 1324–1336 RSC.
- P. G. Collins, M. S. Arnold and P. Avouris, Science, 2001, 292, 706–709 CrossRef CAS PubMed.
- C.-M. Yang, K. H. An, J. S. Park, K. A. Park, S. C. Lim, S.-H. Cho, Y. S. Lee, W. Park, C. Y. Park and Y. H. Lee, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 075419 CrossRef.
- R. Krupke, F. Hennrich, H. v. Löhneysen and M. M. Kappes, Science, 2003, 301, 344–347 CrossRef CAS PubMed.
- M. S. Arnold, A. A. Green, J. F. Hulvat, S. I. Stupp and M. C. Hersam, Nat. Nanotechnol., 2006, 1, 60–65 CrossRef CAS PubMed.
- M. S. Strano, C. A. Dyke, M. L. Usrey, P. W. Barone, M. J. Allen, H. Shan, C. Kittrell, R. H. Hauge, J. M. Tour and R. E. Smalley, Science, 2003, 301, 1519–1522 CrossRef CAS PubMed.
- F. Liang, J. M. Beach, K. Kobashi, A. K. Sadana, Y. I. Vega-Cantu, J. M. Tour and W. E. Billups, Chem. Mater., 2006, 18, 4764–4767 CrossRef CAS.
- J. Chattopadhyay, A. K. Sadana, F. Liang, J. M. Beach, Y. Xiao, R. H. Hauge and W. E. Billups, Org. Lett., 2005, 7, 4067–4069 CrossRef CAS PubMed.
- B. Gebhardt, F. Hof, C. Backes, M. Müller, T. Plocke, J. Maultzsch, C. Thomsen, F. Hauke and A. Hirsch, J. Am. Chem. Soc., 2011, 133, 19459–19473 CrossRef CAS PubMed.
- B. Gebhardt, Z. Syrgiannis, C. Backes, R. Graupner, F. Hauke and A. Hirsch, J. Am. Chem. Soc., 2011, 133, 7985–7995 CrossRef CAS PubMed.
- F. Hof, F. Hauke and A. Hirsch, Chem. Commun., 2014, 50, 6582–6584 RSC.
- F. Hof, R. A. Schäfer, C. Weiss, F. Hauke and A. Hirsch, Chem. – Eur. J., 2014, 20, 16644–16651 CrossRef CAS PubMed.
- F. Hof, S. Bosch, J. M. Englert, F. Hauke and A. Hirsch, Angew. Chem., Int. Ed., 2012, 51, 11727–11730 CrossRef CAS PubMed.
- F. Hof, S. Bosch, S. Eigler, F. Hauke and A. Hirsch, J. Am. Chem. Soc., 2013, 135, 18385–18395 CrossRef CAS PubMed.
- G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15–50 CrossRef CAS.
- P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953 CrossRef.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- M. Methfessel and A. T. Paxton, Phys. Rev. B: Condens. Matter Mater. Phys., 1989, 40, 3616–3621 CrossRef CAS.
- J. T. Frey and D. J. Doren, TubeGen 3.4, 2011, http://turin.nss.udel.edu/research/tubegenonline.html Search PubMed.
- H. J. Monkhorst and J. D. Pack, Phys. Rev. B: Solid State, 1976, 13, 5188–5192 CrossRef.
- J. Gebhardt, F. Viñes and A. Görling, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 86, 195431 CrossRef.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed.
- C. L. Kane and E. J. Mele, Phys. Rev. Lett., 1997, 78, 1932–1935 CrossRef CAS.
- L. Yang and J. Han, Phys. Rev. Lett., 2000, 85, 154–157 CrossRef CAS PubMed.
- J.-C. Charlier, X. Blase and S. Roche, Rev. Mod. Phys., 2007, 79, 677–732 CrossRef CAS.
- M. Ouyang, J.-L. Huang, C. L. Cheung and C. M. Lieber, Science, 2001, 292, 702–705 CrossRef CAS PubMed.
- J. W. Mintmire and C. T. White, Phys. Rev. Lett., 1998, 81, 2506–2509 CrossRef CAS.
- G. Bertoni and L. Calmels, Micron, 2006, 37, 486–491 CrossRef CAS PubMed.
- T. Miyake and S. Saito, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 68, 155424 CrossRef.
- X. Yang and J. Ni, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 69, 125419 CrossRef.
- X. Yang and J. Ni, Comput. Phys. Commun., 2005, 169, 20–23 CrossRef CAS.
- Y.-L. Mao, X.-H. Yan and Y. Xiao, Nanotechnology, 2005, 16, 3092–3096 CrossRef CAS.
- A. Lugo-Solis and I. Vasiliev, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 76, 235431 CrossRef.
- F. Ancilotto and F. Toigo, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 13713–13721 CrossRef CAS.
- D. Lamoen and B. N. J. Persson, J. Chem. Phys., 1998, 108, 3332–3341 CrossRef CAS.
- Y. Miyamoto, A. Rubio, X. Blase, M. L. Cohen and S. G. Louie, Phys. Rev. Lett., 1995, 74, 2993–2996 CrossRef CAS PubMed.
- G. Gao, T. Çagin and W. A. Goddard III, Phys. Rev. Lett., 1998, 80, 5556–5559 CrossRef CAS.
- A. Hansson and S. Stafström, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 72, 125420 CrossRef.
- T. Miyake and S. Saito, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 65, 165419 CrossRef.
- G. Henkelman, A. Arnaldsson and H. Jonsson, Comput. Mater. Sci., 2006, 36, 354–360 CrossRef.
- B. Akdim, X. Duan, D. A. Shiffler and R. Pachter, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 72, 121402 CrossRef.
- V. Zólyomi and J. Kürti, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 70, 085403 CrossRef.
- L. Duclaux, Carbon, 2002, 40, 1751–1764 CrossRef CAS.
- D. Wunderlich, F. Hauke and A. Hirsch, Chem. – Eur. J., 2008, 14, 1607–1614 CrossRef CAS PubMed.
- A. Pénicaud, P. Poulin, A. Derré, E. Anglaret and P. Petit, J. Am. Chem. Soc., 2005, 127, 8–9 CrossRef PubMed.
- D. Paolucci, M. M. Franco, M. Iurlo, M. Marcaccio, M. Prato, F. Zerbetto, A. Pénicaud and F. Paolucci, J. Am. Chem. Soc., 2008, 130, 7393–7399 CrossRef CAS PubMed.
- S. Fogden, C. A. Howard, R. K. Heenan, N. T. Skipper and M. S. P. Shaffer, ACS Nano, 2012, 6, 54–62 CrossRef CAS PubMed.
- D. Voiry, C. Vallés, O. Roubeau and A. Pénicaud, Carbon, 2011, 49, 170–175 CrossRef CAS.
- F. Liang, A. K. Sadana, A. Peera, J. Chattopadhyay, Z. Gu, R. H. Hauge and W. E. Billups, Nano Lett., 2004, 4, 1257–1260 CrossRef CAS.
- D. Voiry, O. Roubeau and A. Pénicaud, J. Mater. Chem., 2010, 20, 4385–4391 RSC.
- M. S. Dresselhaus, G. Dresselhaus, R. Saito and A. Jorio, Phys. Rep., 2005, 409, 47–99 CrossRef.
- J. M. Englert, P. Vecera, K. C. Knirsch, R. A. Schäfer, F. Hauke and A. Hirsch, ACS Nano, 2013, 7, 5472–5482 CrossRef CAS PubMed.
- H. Telg, J. Maultzsch, S. Reich, F. Hennrich and C. Thomsen, Phys. Rev. Lett., 2004, 93, 177401 CrossRef CAS PubMed.
- R. B. Weisman and S. M. Bachilo, Nano Lett., 2003, 3, 1235–1238 CrossRef CAS.
- S. Kuwahara, Y. Kuwahara and H. Shinohara, J. Nanomater., 2014, 2014, 1–7 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available: Experimental details regarding the reductive charging of HiPco SWCNTs and additional Raman and fluorescence analysis. In addition, theoretical details of the adsorption geometries of potassium on chiral SWCNTs and SWCNT bundle structures. See DOI: 10.1039/c5tc01407g |
| This journal is © The Royal Society of Chemistry 2017 |